考向18 特殊的四边形（能力提升）-2021年中考数学一轮基础知识复习和专题巩固提升训练课件PPT

这是一份考向18 特殊的四边形（能力提升）-2021年中考数学一轮基础知识复习和专题巩固提升训练课件PPT，共16页。
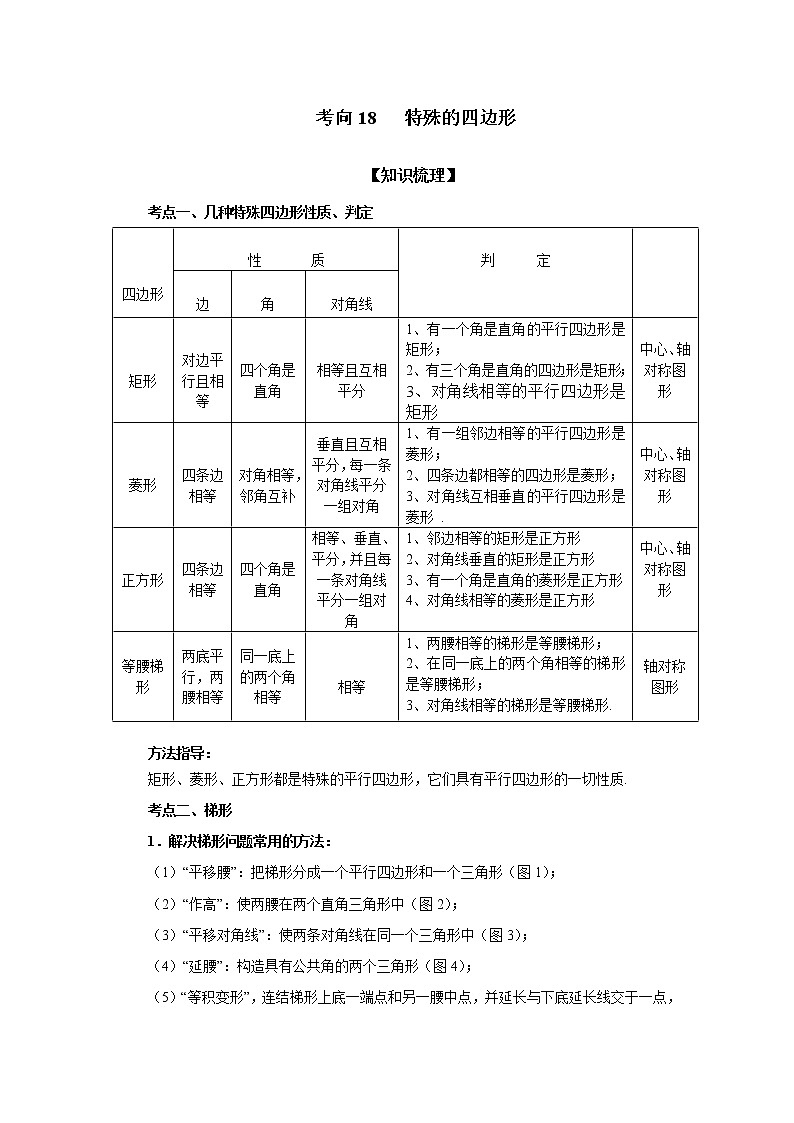
考向18   特殊的四边形 【知识梳理】考点一、几种特殊四边形性质、判定  四边形 性       质 判      定   边 角 对角线 矩形 对边平行且相等 四个角是直角 相等且互相平分1、有一个角是直角的平行四边形是矩形；2、有三个角是直角的四边形是矩形；3、对角线相等的平行四边形是矩形中心、轴对称图形 菱形 四条边相等 对角相等，邻角互补垂直且互相平分，每一条对角线平分一组对角1、有一组邻边相等的平行四边形是菱形；2、四条边都相等的四边形是菱形；3、对角线互相垂直的平行四边形是菱形 .中心、轴对称图形正方形四条边相等四个角是直角相等、垂直、平分，并且每一条对角线平分一组对角1、邻边相等的矩形是正方形2、对角线垂直的矩形是正方形3、有一个角是直角的菱形是正方形4、对角线相等的菱形是正方形中心、轴对称图形 等腰梯形两底平行，两腰相等同一底上的两个角相等 相等1、两腰相等的梯形是等腰梯形；2、在同一底上的两个角相等的梯形是等腰梯形；3、对角线相等的梯形是等腰梯形.轴对称图形 方法指导：矩形、菱形、正方形都是特殊的平行四边形，它们具有平行四边形的一切性质.考点二、梯形1．解决梯形问题常用的方法：（1）“平移腰”：把梯形分成一个平行四边形和一个三角形（图1）；
（2）“作高”：使两腰在两个直角三角形中（图2）；
（3）“平移对角线”：使两条对角线在同一个三角形中（图3）；
（4）“延腰”：构造具有公共角的两个三角形（图4）；
（5）“等积变形”，连结梯形上底一端点和另一腰中点，并延长与下底延长线交于一点，构成三角形（图5）． 
　  　　 图1 　　　　　图2 　　　　　　图3 　　　　　　 图4 　　　　图5 
    方法指导：解决梯形问题的基本思想和方法就是通过添加适当的辅助线，把梯形问题转化为已经熟悉的平行四边形和三角形问题来解决．在学习时注意它们的作用，掌握这些辅助线的使用对于学好梯形内容很有帮助．2.特殊的梯形（1）等腰梯形：两腰相等的梯形叫做等腰梯形．性质：①等腰梯形的同一底边上的两个角相等；等腰梯形的两条对角线相等．②同一底边上的两个角相等的梯形是等腰梯形．③等腰梯形是轴对称图形，它的对称轴是经过两底中点的一条直线．（2）直角梯形：有一个角是直角的梯形叫做直角梯形．考点三、中点四边形相关问题1.中点四边形的概念：把依次连接任意一个四边形各边中点所得的四边形叫做中点四边形．2.若中点四边形为矩形，则原四边形满足条件对角线互相垂直；
若中点四边形为菱形，则原四边形满足条件对角线相等；
若中点四边形为正方形，则原四边形满足条件对角线互相垂直且相等．方法指导：中点四边形的形状由原四边形的对角线的位置和数量关系决定．       【专项训练】一、选择题1. 如图,E是边长为1的正方形ABCD的对角线BD上一点，且BE=BC，P为CE上任意一点，PQ⊥BC于点Q，PR⊥BE于点R，则PQ＋PR的值是(      )． A． 　　　B． 　　　C． 　　　D．
 2．如图,在梯形ABCD中， AB∥CD， 中位线MN = 7,对角线AC⊥BD,∠BDC = 30°，则梯形的高为（      ）．A． 　　　B．　　　 C． 　　　D．
 3. 四边形ABCD的对角线AC=BD，且AC⊥BD，分别过A、B、C、D作对角线的平行线，得到四边形EFGH，则它是（     ）.A．正方形 　　　B．菱形 　　　C．矩形　　　 D．任意四边形4. 如图，矩形ABCD中，其长为a，宽为b，如果，则的值为（    ）.
　  A．　　　 B．　　　 C． 　　　D．
  5. 如图，在菱形ABCD中，，的垂直平分线FE交对角线AC于点F，E为垂足，连接DF．则等于（     ）．　A． 　　　B． 　　　C．　　　 D．
 6. 如图，在正方形ABCD中，点P是AB上一动点（不与A、B重合），对角线AC、BD相交于点O，过点P分别作AC、BD的垂线，分别交AC、BD于点E、F，交AD、BC于点M、N．下列结论：①△APE≌△AME；②PM+PN=AC；③PE2+PF2=PO2；④△POF∽△BNF；其中正确的结论有（　　）A．4个 B．3个 C．2个 D．1个二、填空题7. 如图，点E、F、G、H分别为正方形ABCD的边AB、BC、CD、DA上的点，且AE=BF=CG=DH=AB，则图中阴影部分的面积与正方形ABCD的面积之比为___________．
　 8. 如图，在等腰梯形ABCD中，AD∥BC，AC与BD相交于点O．下面结论正确的是_________．
①AC=BD；②∠DAO=∠DBC；③S△BOC=S梯形ABCD；④△AOB≌△DOC．
 9. 如图，圆柱形玻璃杯，高为8cm，底面周长为12cm，在杯内离杯底2cm的点C处有一滴蜂蜜，此时一只蚂蚁正好在杯外壁，离杯上沿2cm与蜂蜜相对的点A处，求蚂蚁到达蜂蜜的最短距离是            ．如图，将正△ABC分割成m个边长为1的小正三角形和一个黑色菱形，这个黑色菱形可分割成n个边长为1的小三角形，若=，则△ABC的边长是_________.如图，在梯形ABCD中，AD∥BC，∠C=90°，BE平分∠ABC且交CD于E，E为CD的中点，EF∥BC交AB于F，EG∥AB交BC于G，当AD=2，BC=12时，四边形BGEF的周长为_________． 12.如图，以菱形ABCD各边的中点为顶点作四边形A1B1C1D1，再以A1B1C1D1各边的中点为顶点作四边形A2B2C2D2，…，如此下去，得到四边形A2011B2011C2011D2011，若ABCD对角线长分别为a和b，请用含a、b的代数式表示四边形A2011B2011C2011D2011的周长_________________. 三、解答题13. 已知，如图，正方形ABCD的边长为6，菱形EFGH的三个顶点E，G，H分别在正方形ABCD边AB，CD，DA上，AH=2，连接CF．
　　(1)当DG=2时，求△FCG的面积；
　　(2)设DG=，用含的代数式表示△FCG的面积；
　　(3)判断△FCG的面积能否等于1，并说明理由．             在图1到图3中，点O是正方形ABCD对角线AC的中点，△MPN为直角三角形，∠MPN=90°．正方形ABCD保持不动，△MPN沿射线AC向右平移，平移过程中P点始终在射线AC上，且保持PM垂直于直线AB于点E，PN垂直于直线BC于点F．
（1）如图1，当点P与点O重合时，OE与OF的数量关系为______；
（2）如图2，当P在线段OC上时，猜想OE与OF有怎样的数量关系与位置关系？并对你的猜想结果给予证明；
（3）如图3，当点P在AC的延长线上时，OE与OF的数量关系为_______；位置关系为_________．
                 15．如图1，P是线段AB上的一点，在AB的同侧作△APC和△BPD，使PC=PA，PD=PB，∠APC=∠BPD，连接CD，点E、F、G、H分别是AC、AB、BD、CD的中点，顺次连接E、F、G、H．
    （1）猜想四边形EFGH的形状，直接回答，不必说明理由；
    （2）当点P在线段AB的上方时，如图2，在△APB的外部作△APC和△BPD，其他条件不变，（1）中的结论还成立吗？说明理由；
    （3）如果（2）中，∠APC=∠BPD=90°，其他条件不变，先补全图3，再判断四边形EFGH的形状，并说明理由．
                  16. 如图，在平面直角坐标系中，点A（10，0），∠OBA=90°，BC∥OA，OB=8，点E从点B出发，以每秒1个单位长度沿BC向点C运动，点F从点O出发，以每秒2个单位长度沿OB向点B运动．现点E、F同时出发，当点F到达点B时，E、F两点同时停止运动．
（1）求梯形OABC的高BG的长；
（2）连接E、F并延长交OA于点D，当E点运动到几秒时，四边形ABED是等腰梯形；
（3）动点E、F是否会同时在某个反比例函数的图象上？如果会，请直接写出这时动点E、F运动的时间t的值；如果不会，请说明理由．                答案与解析一.选择题1．【答案】A．2．【答案】B.3．【答案】A.4．【答案】A.【解析】由题意，，.5．【答案】D.6．【答案】B.【解析】在正方形ABCD中，∠PAE=∠MAE=45°，在△APE和△AME中，，∴△APE≌△AME（ASA），故①正确；∴AP=AM，∴△APM是等腰直角三角形，∴PM=AP，同理可得PN=PB，∴PM+PN=AB，又∵AC=AB，∴PM+PN=AC，故②正确；∵PM⊥AC，PN⊥BD，AC⊥BD，∴四边形PEOF是矩形，∴PF=OE，在Rt△POE中，PE2+OE2=PO2，∴PE2+PF2=PO2，故③正确；∵矩形PEOF不一定是正方形，∴△POF是不一定等腰直角三角形，∵∠OBC=45°，BF⊥FN，∴△BNF是等腰直角三角形，∴△POF与△BNF相似不一定成立，故④错误；综上所述，正确的结论有①②③共3个．故选B．二．填空题7．【答案】.【解析】 把△APD旋转到△DCM，把△ABF旋转到△BCN， 则多边形PFBNMD的面积被分成10份，阴影部分占4份.8．【答案】①②④.9．【答案】10cm. 【解析】如图：将杯子侧面展开，作A关于EF的对称点A′，连接A′C，则A′C即为最短距离，由题意可得出：A′D=6cm，CD=8cm，A′C==10（cm）．10.【答案】12.【解析】设正△ABC的边长为x，则高为x，S△ABC=x•x=x2，
∵所分成的都是正三角形，∴结合图形可得黑色菱形的较长的对角线为x-，较短的对角线为（x-）=x-1，
∴黑色菱形的面积=（x-）（x-1）=（x-2）2，
∴=，整理得，11x2-144x+144=0，
解得x1=（不符合题意，舍去），x2=12，所以，△ABC的边长是12．11.【答案】28.【解析】先根据EF∥BC交AB于F，EG∥AB交BC于G得出四边形BGEF是平行四边形，再由BE平分∠ABC且交CD于E可得出∠FBE=∠EBC，由EF∥BC可知，∠EBC=∠FEB，故∠FBE=FEB，由此可判断出四边形BGEF是菱形，再根据E为CD的中点，AD=2，BC=12求出EF的长，进而可得出结论．12．【答案】.【解析】结合图形，脚码为奇数时，四边形A2n-1B2n-1C2n-1D2n-1是矩形，长为 ，宽为 ；
脚码为偶数时，四边形A2nB2nC2nD2n是菱形，边长为 ，
∴四边形A2010B2010C2010D2010是菱形，边长为 ，
周长为 ，即 ．
∴四边形A2011B2011C2011D2011是矩形，长为，宽为，
∴四边形A2011B2011C2011D2011的周长为：2（+）=．故答案为：．三.综合题13．【解析】(1).
(2)作FM⊥DC，M为垂足，连结GE，
∵ AB∥CD，∴ ∠AEG=∠MGE，
∵ HE∥GF，∴ ∠HEG=∠FGE．
∴ ∠AEH=∠MGF.
在△AHE和△MFG中，∠A=∠M=90°，HE=FG，
∴ △AHE≌△MFG.
∴ FM=HA=2， 即无论菱形EFGH如何变化，点F的直线CD的距离始终为定值2.
因此
(3)若，由，得，此时在△DGH中，.
相应地，在△AHE中，，即点E已经不在边AB上.
故不可能有.14．【解析】（1）OE=OF（相等）；
（2）OE=OF，OE⊥OF；
证明：连接BO，
∵在正方形ABCD中，O为AC中点，
∴BO=CO，BO⊥AC，∠BCA=∠ABO=45°，
∵PF⊥BC，∠BCO=45°，
∴∠FPC=45°，PF=FC．
∵正方形ABCD，∠ABC=90°，
∵PF⊥BC，PE⊥AB，
∴∠PEB=∠PFB=90°．
∴四边形PEBF是矩形，
∴BE=PF．
∴BE=FC．
∴△OBE≌△OCF，
∴OE=OF，∠BOE=∠COF，
∵∠COF+∠BOF=90°，
∴∠BOE+∠BOF=90°，
∴∠EOF=90°，
∴OE⊥OF．
（3）OE=OF（相等），OE⊥OF（垂直）． 15．【解析】（1）四边形EFGH是菱形．
（2）成立．理由：连接AD，BC．
∵∠APC=∠BPD，
∴∠APC+∠CPD=∠BPD+∠CPD．
即∠APD=∠CPB．
又∵PA=PC，PD=PB，
∴△APD≌△CPB（SAS）∴AD=CB．
∵E、F、G、H分别是AC、AB、BD、CD的中点，
∴EF、FG、GH、EH分别是△ABC、△ABD、△BCD、△ACD的中位线．
∴EF=BC，FG=AD，GH=BC，EH=AD．
∴EF=FG=GH=EH．∴四边形EFGH是菱形．
（3）补全图形．
判断四边形EFGH是正方形．
理由：连接AD，BC．
∵（2）中已证△APD≌△CPB．
∴∠PAD=∠PCB．
∵∠APC=90°，
∴∠PAD+∠1=90°．
又∵∠1=∠2．
∴∠PCB+∠2=90°．
∴∠3=90°．
∵（2）中已证GH，EH分别是△BCD，△ACD的中位线，
∴GH∥BC，EH∥AD．
∴∠EHG=90°．
又∵（2）中已证四边形EFGH是菱形，
∴菱形EFGH是正方形.16.【解析】（1）根据题意，AB==6,
∵2S△AOB=AB•OB=AO•BG，∴BG===4.8；
（2）设当E点运动到x秒时，四边形ABED是等腰梯形，则BE=x，OF=2x，
∵BC∥OA，
∴=，即=，解得OD=，
过E作EH⊥OA于H，
∵四边形ABED是等腰梯形，
∴DH=AG=，HG=BE=x，
∴DH=10--x-3.6=3.6，解得x=；

（3）会同时在某个反比例函数的图象上．
根据题意，OG=AO-AG=10-3.6=6.4，
∴点E（6.4-t，4.8），
∵OF=2t，
∴2tcos∠AOB=2t×=t，2tsin∠AOB=2t×=t，
∴点F的坐标为（t，t）
假设能在同一反比例函数图象上，则t×t=（6.4-t）×4.8，
整理得：2t2+5t-32=0，
△=25-4×2×（-32）=281＞0，
∴方程有解，即E、F会同时在某一反比例函数图象上，此时，t=，
因此E、F会同时在某个反比例函数的图象上，t=．