专题10 胡不归问题-2022年中考数学二次函数解答题题型全归纳（全国通用）

这是一份专题10 胡不归问题-2022年中考数学二次函数解答题题型全归纳（全国通用），文件包含专题10胡不归问题解析版docx、专题10胡不归问题原卷版docx等2份试卷配套教学资源，其中试卷共27页， 欢迎下载使用。

（1）求抛物线的解析式及顶点D的坐标；
（2）点P为抛物线在直线BC下方图形上的一动点，当△PBC面积最大时，求点P的坐标；
（3）若点Q为线段OC上的一动点，问：AQ+12QC是否存在最小值？若存在，求出这个最小值；若不存在，请说明理由．
【解答】解：（1）函数的表达式为：y＝a（x﹣1）（x﹣3）＝a（x2﹣4x+3），
即：3a＝3，解得：a＝1，
故抛物线的表达式为：y＝x2﹣4x+3，
则顶点D（2，﹣1）．
（2）将点B、C的坐标代入一次函数表达式：y＝mx+n并解得：
直线BC的表达式为：y＝﹣x+3，
过点P作y轴的平行线交BC于点H，
设点P（x，x2﹣4x+3），则点H（x，﹣x+3），
则S△PBC=12•PH×OB=32（﹣x+3﹣x2+4x﹣3）=32（﹣x2+3x），
∵-32＜0，故S△PBC有最大值，此时x=32，
故点P（32，-34）．
（3）存在，理由：
如上图，过点C作与y轴夹角为30°的直线CG，作QH⊥GH，垂足为G，
则GQ=12CQ，
AQ+12QC最小值＝AQ+GQ＝AG，
直线GC所在表达式中的k值为3，直线GC的表达式为：y=3x+3…①，
则直线AG所在表达式中的k值为-33，
则直线AG的表达式为：y=-33x+s，将点A的坐标代入y=-33x+s并解得：s=33，
则直线AG的表达式为：y=-33x+33⋯②，
联立①②并解得：x=1-334，
故点G（1-334，3+34），而点A（1，0），
则AG=3+32，
即：AQ+12QC的最小值为3+32．
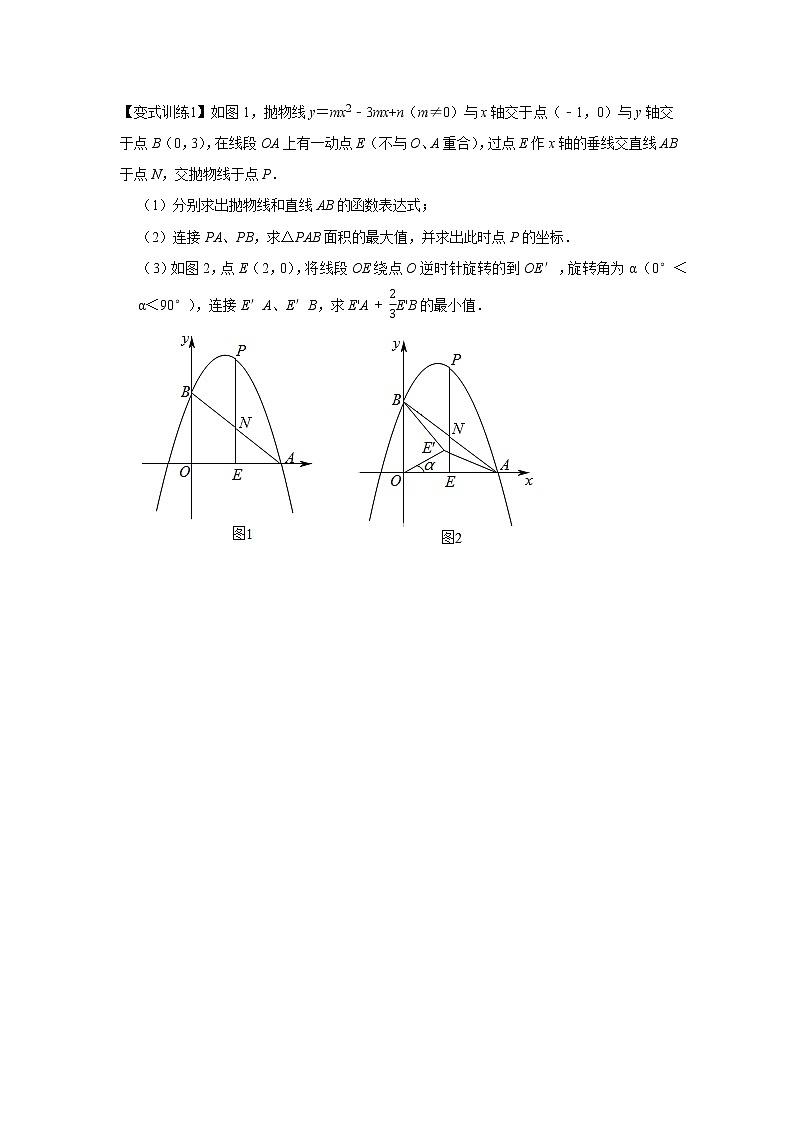
如图1，抛物线y＝mx2﹣3mx+n（m≠0）与x轴交于点（﹣1，0）与y轴交于点B（0，3），在线段OA上有一动点E（不与O、A重合），过点E作x轴的垂线交直线AB于点N，交抛物线于点P．
（1）分别求出抛物线和直线AB的函数表达式；
（2）连接PA、PB，求△PAB面积的最大值，并求出此时点P的坐标．
（3）如图2，点E（2，0），将线段OE绕点O逆时针旋转的到OE′，旋转角为α（0°＜α＜90°），连接E′A、E′B，求E'A+23E'B的最小值．
【解答】解：（1）∵抛物线y＝mx2﹣3mx+n（m≠0）与x轴交于点C（﹣1，0）与y轴交于点B（0，3），
则有n=3m+3m+n=0，解得m=-34n=3，
∴抛物线y=-34x2+94x+3，
令y＝0，得到-34x2+94x+3＝0，
解得：x＝4或﹣1，
∴A（4，0），B（0，3），
设直线AB解析式为y＝kx+b，则b=34k+b=0，解得k=-34b=3，
∴直线AB解析式为y=-34x+3；
（2）如图1中，设P（x，-34x2+94x+3），则点N（x，-34x+3），
则设△PAB面积为S，
则S＝S△PNA+S△PNB=12×PN×OA=12×4×（-34x2+94x+3+34x﹣3）=-32x2+6x，
∵-32＜0，故S有最大值，当x＝2时，S的最大值为6，此时P（2，4.5）；
（3）如图2中，在y轴上取一点M′使得OM′=43，连接AM′，在AM′上取一点E′使得OE′＝OE．
∵OE′＝2，OM′•OB=43×3＝4，
∴OE′2＝OM′•OB，
∴OE'OM'=OBOE'，
∵∠BOE′＝∠M′OE′，
∴△M′OE′∽△E′OB，
∴M'E'BE'=OE'OB=23，
∴M′E′=23BE′，
∴AE′+23BE′＝AE′+E′M′＝AM′，此时AE′+23BE′最小（两点间线段最短，A、M′、E′共线时），
最小值＝AM′=42+(43)2=4103．
如图，已知二次函数y＝﹣x2+bx+3的图象与x轴交于点A，点B（3，0），交y轴于点C，点M（m，0）是线段OB上一点（与点O、B不重合），过点M作MP⊥x轴，交BC于点P，交抛物线于点Q，连接OP，CQ．
（1）求二次函数的表达式；
（2）若∠COP＝∠QCP，求QP的长；
（3）若△CPQ是以CP为底边的等腰三角形，点N是线段OC上一点，连接MN，求MN+13CN的最小值．
【解答】解：（1）将点B的坐标代入抛物线表达式得：0＝﹣9+3b+3，解得：b＝2，
故抛物线的表达式为：y＝﹣x2+2x+3；
（2）对于y＝﹣x2+2x+3，令x＝0，则y＝3，故点C（0，3），
则OB＝OC＝3，故∠OCB＝∠OBC＝45°，
设直线BC的表达式为：y＝kx+b，则3k+b=0b=3，解得：k=-1b=3，
故直线BC的表达式为：y＝﹣x+3，
点M的坐标为：（m，0），则点P、Q的坐标分别为：（m，3﹣m）、（m，﹣m2+2m+3），
则PQ＝（﹣m2+2m+3）﹣（3﹣m）＝﹣m2+3m；
∵PQ∥y轴，
∴∠OCP＝∠CPQ，
∵∠COP＝∠QCP，
∴△OPC∽△CQP，
∴OCPC=PCPQ，即PC2＝OC•PQ，
∴2m2＝3（﹣m2+3m），
解得：m＝0（舍去）或95，
故PQ＝﹣m2+3m=5425；
（3）∵PQ∥y轴，
∴∠OCP＝∠CPQ，
∵△CPQ是以CP为底边的等腰三角形，
∴∠QCP＝∠QPC，
∴∠QCP＝∠PCO＝45°，
∴∠OCQ＝90°，即CQ∥x轴，
故点C、Q关于函数对称性直线x＝1对称，故点Q的坐标为：（2，3）；
过点C作直线l，过点M作MH⊥l交于点H，交y轴于点N，则点M、N为所求点，
设直线l与y轴负半轴夹角的正弦值为13，即sin∠HCN=13=sin∠NMO，则tan∠NMO=24，
则NH=13CN，
∴MN+13CN＝MN+NH为最小，
∵tan∠NMO=24，
∴设直线MH的表达式为：y=-24x+t，
将点M（2，0）的坐标代入上式并解得：t=22，
故点N（0，22），
则CN＝OC﹣ON＝3-22，
∴MN+13CN的最小值＝MN+NH＝MN+13CN=22+(22)2+13×（3-22）=3+423．
如图1，在平面直角坐标系中，抛物线y＝ax2+bx﹣4与x轴交于点A（﹣2，0）、B（4，0），与y轴交于点C．E为抛物线上一点，直线AE交y轴于点D，且OD＝OA．
（1）求抛物线的解析式；
（2）点P是第四象限内的抛物线上一点，过点P作PQ∥y轴交直线AE于点Q，交x轴于点F，过点P作PG⊥AE于点G，交x轴于点H，求PQ-22GQ的最大值，并求出此时点P的坐标；
（3）如图2，点K为线段OD的中点，作射线AK，将该抛物线沿射线AK方向平移52个单位长度，得到新抛物线y1＝a1x2+b1x+c1（a1≠0），新抛物线与原抛物线交于点I．点N是平面内一点，点M是新抛物线上一点，若以点I、E、M、N为顶点的四边形是以IE为边的矩形，请直接写出点N的坐标．
【解答】解：（1）设抛物线的表达式为y＝a（x﹣x1）（x﹣x2）＝a（x+2）（x﹣4）＝a（x2﹣2x﹣8），
则﹣8a＝﹣4，解得a=12，
抛物线的表达式为y=12x2﹣x﹣4①；
（2）∵OA＝OD＝2，故点D（0，2），
由点A、D的坐标得，直线AE的表达式为y＝x+2，
设点P的坐标为（x，12x2﹣x﹣4），则点Q（x，x+2），
∵OA＝OD，故∠QAK＝45°，
而GP⊥AE，则△PQG为等腰直角三角形，
过点G作GK⊥PQ于点K，则QK＝PK=22GQ，
则PQ-22GQ＝PQ﹣QK＝PK=12PQ=12（x+2-12x2+x+4）=-14x2+x+3，
∵-14＜0，故抛物线开口向下，
∴PQ-22GQ有最大值，当x＝2时，PQ-22GQ的最大值为4，
此时点P（2，﹣4）；
（3）联立y=12x2﹣x﹣4和y＝x+2并解得x=6y=8，故点E（6，8），
∵点K为线段OD的中点，则点K（0，1），
∴tanKAO=OKOA=12，则sin∠KAO=15，cs∠KAO=25，
则该抛物线沿射线AK方向平移52个单位长度相当于向右平移1个单位向上平移12个单位，
则平移后的抛物线为y=12（x﹣1）2﹣（x﹣1）﹣4+12=12（x﹣2）2﹣4=12x2﹣2x﹣2②；
联立①②并解得x=2y=-4，
故点I的坐标为（2，﹣4），
设点M（m，n），n=12m2﹣2m﹣2③，
而点E（6，8），
则点I向右平移4个单位向上平移12个单位得到点E，
同样，点M（N）向右平移4个单位向上平移12个单位N（M）且EM＝MI（EN＝MI），
当点M在点N的下方时，
即m+4＝s④，n+12＝t⑤，（m﹣6）2+（n﹣8）2＝（m+2）2+（n+16）2⑥，
将④⑤代入⑥并整理得：m+3n﹣10＝0⑦，
联立②⑦并解得m=163n=149或m=-2n=4⑧，
则s=283t=1229或s=2t=16，
故点N的坐标为（283，1229）或（2，16）；
当点M在点N的上方时，
则m﹣4＝s，n﹣12＝t，（s﹣6）2+（t﹣8）2＝（m﹣2）2+（n+4）2，
同理可得，点N的坐标为（457-73，-23-4579）或（-457-73，-23+4579）；
综上，点N的坐标为（283，1229）或（2，16）或（457-73，-23-4579）或（-457-73，-23+4579）．
如图，在平面直角坐标系中，点A在抛物线y＝﹣x2+4x上，且横坐标为1，点B与点A关于抛物线的对称轴对称，直线AB与y轴交于点C，点D为抛物线的顶点，点E的坐标为（1，1）．
（1）求线段AB的长；
（2）点P为线段AB上方抛物线上的任意一点，过点P作AB的垂线交AB于点H，点F为y轴上一点，当△PBE的面积最大时，求PH的长度；
（3）在（2）中，HF+12FO取得最小值时，将△CFH绕点C顺时针旋转60°后得到△CF′H′，过点F′作CF′的垂线与直线AB交于点Q，点R为抛物线对称轴上的一点，在平面直角坐标系中是否存在点S，使以点D、Q、R、S为顶点的四边形为菱形，若存在，请直接写出点S的坐标，若不存在，请说明理由．
【解答】解：（1）当x＝1时，y＝﹣x2+4x＝3，故点A（1，3），
由抛物线的表达式知，其对称轴为直线x＝2，故点B（3，3），
∴AB＝2；
（2）如图1中，设P（m，﹣m2+4m），作PN∥y轴交BE于N．
∵直线BE的解析式为y＝x，
∴N（m，m），
∴S△PEB=12×2×（﹣m2+3m）＝﹣m2+3m，
∴当m=32时，△PEB的面积最大，此时P（32，154），H（32，3），
∴PH=154-3=34；
（3）存在，理由：
如图1，作直线OG交AB于G，使得∠COG＝30°，作HK⊥OG于K交OC于F，
∵FK=12OF，
∴HF+12FO＝FH+FK＝HK，此时HF+12OF的值最小，
∵S△OGH=12•HG•OC=12•OG•HK，
∴HK=3×(3+32)23=32+334，
∴HF+12OF的最小值为=32+334，
如图2中，由题意CH=32，CF=32，QF′=12，CQ＝1，
∴Q（﹣1，3），D（2，4），DQ=10，
①当DQ为菱形的边时，
则DQ＝QS1=10，而点Q（﹣1，3），则点S1（﹣1，3-10），
同理可得：S2（﹣1，3+10），S4（5，3）；
②当DQ为对角线时，同理可得S3（﹣1，8），
综上所述，满足条件的点S坐标为（﹣1，3-10）或（﹣1，3+10）或（﹣1，8）或（5，3）．
如图1，抛物线y=24x2+2x﹣62交x轴于A、B两点（点A在点B的左侧），交y轴于C点，D点是该抛物线的顶点，连接AC、AD、CD．
（1）求△ACD的面积；
（2）如图1，点P是线段AD下方的抛物线上的一点，过P作PE∥y轴分别交AC于点E，交AD于点F，过P作PG⊥AD于点G，求EF+52FG的最大值，以及此时P点的坐标；
（3）如图2，在对称轴左侧抛物线上有一动点M，在y轴上有一动点N，是否存在以BN为直角边的等腰Rt△BMN？若存在，求出点M的横坐标，若不存在，请说明理由．
【解答】解：（1）令x＝0，得y=24x2+2x﹣62=-62，
∴C（0，﹣62），
令y＝0，得y=24x2+2x﹣62=0，
解得，x＝﹣62或22，
∴A（﹣62，0），点B（22，0），
设直线AC的解析式为：y＝kx+b（k≠0），
则-62k+b=0b=-62，
∴k=-1b=-62，
∴直线AC的解析式为：y＝﹣x﹣62，
∵y=24x2+2x﹣62=24（x+22）2﹣82，
∴D（﹣22，﹣82），
过D作DM⊥x轴于点M，交AC于点N，如图1，
则N（﹣22，﹣42），
∴DN=42，
∴△ACD的面积=12DN⋅OA=12×42×62=24；
（2）如图1，过点D作x轴的平行线交FP的延长线于点H，
由点A、D的坐标得，直线AD的表达式为：y＝﹣2x﹣122，
故tan∠FDH＝2，则sin∠FDH=25，
∵∠HDF+∠HFD＝90°，∠FPG+∠PFG＝90°，
而∠HFD＝∠PFG，
∴∠FPG＝∠FDH，
在Rt△PGF中，PF=FGsin∠PFH=FGsin∠FDH=52FG，
则EF+52FG＝EF+PF＝EP，
设点P（x，24x2+2x﹣62），则点E（x，﹣x﹣62），
则EF+52FG＝EF+PF＝EP＝﹣x﹣62-（24x2+2x﹣62）=-24x2﹣3x，
∵-24＜0，故EP有最大值，此时x=-b2a=-32，最大值为922；
当x＝﹣32时，y=24x2+2x﹣62=-1522，
故点P（﹣32，-1522）；
（3）存在，理由：
设点M的坐标为（m，n），则n=24m2+2m﹣62①，点N（0，s），
（Ⅰ）当点M在x轴下方时，
①当∠MNB为直角时，如图2，
过点N作x轴的平行线交过点B与y轴的平行线于点H，交过点M与y轴的平行线于点G，
∵∠MNG+∠BNH＝90°，∠MNG+∠GMN＝90°，
∴∠GMN＝∠BNH，
∵∠NGM＝∠BHN＝90°，MN＝BN，
∴△NGM≌△BHN（AAS），
∴GN＝BH，MG＝NH，
即n﹣s＝22且﹣m＝﹣s②，
联立①②并解得：m＝﹣22±210（舍去正值），
故m＝﹣22-210；
②当∠NBM为直角时，如图3，
过点B作y轴的平行线交过点N与x轴的平行线于点G，交过点M与x轴的平行线于点H，
同理可证：△MHB≌△BGN（AAS），
则BH＝NG，即n＝﹣22，
当n＝﹣22时，24m2+2m﹣62=-22，解得：m＝﹣22±23（舍去正值），
故m＝﹣22-23；
（Ⅱ）当点M在x轴上方时，
同理可得：m=-2-34或﹣32-34；
综上，点M的横坐标为﹣22-210或﹣22-26或-2-34或﹣32-34．
如图1，在平面直角坐标系中，抛物线y＝ax2+bx+c（a≠0）与x轴交于点A（﹣2，0），点B（4，0），与y轴交于点C（0，2）．
（1）求抛物线的解析式；
（2）点P是第一象限内的抛物线上一点，过点P作PH⊥x轴于点H，交直线BC于点Q，求PQ+55CQ的最大值，并求出此时点P的坐标；
（3）如图2，将抛物线沿射线BC的方向平移5个单位长度，得到新抛物线y1＝a1x2+b1x+c1（a1≠0），新抛物线与原抛物线交于点G．点M是x轴上一点，点N是新抛物线上一点，若以点C、G、M、N为顶点的四边形是平行四边形时，请直接写出点N的坐标．
【解答】解：（1）将点A、B、C的坐标代入抛物线表达式得：4a-2b+c=016a+4b+c=0c=2，
解得a=-14b=12c=2．
故抛物线的表达式为y=-14x2+12x+2①；
（2）由点B、C的坐标得，直线BC的表达式为y=-12x+2，
设点P（m，-14m2+32m+2），则点Q（m，-12m+2），
过点Q作QH⊥y轴于点H，
由点B、C的坐标知，CO＝2，OB＝4，则tan∠CBO=COBO=12=tan∠CQH，则sin∠CQH=55，
则CH＝CQsin∠CQH=55CQ＝CH＝yC﹣yH＝2﹣（-12m+2）=12m，
则PQ+55CQ＝（-14m2+32m+2）﹣（-12m+2）+12m=-14m2+32m，
∵-14＜0，故PQ+55CQ有最大值，
当m＝3时，PQ+55CQ最大值为94，此时点P（3，54）；
（3）将抛物线沿射线BC的方向平移5个单位长度，则向左平移了2个单位，向上平移了1个单位，
则抛物线的抛物线为y=-14（x+1）2+32（x+1）+2+1=-14x2-12x+3②；
联立①②并解得x=1y=94，故点G（1，94），
设点N的坐标为（x，-14x2-12x+3），
①当CG是边时，
将点C向上平移14个单位得到点G，则点N（M）向上平移14个单位得到M（N），
即-14x2-12x+3±14=0，解得x＝﹣1±10或1±22，
故点N的坐标为（﹣1+10，14）或（﹣1-10，14）或（﹣1+22，-14）或（﹣1﹣22，-14）；
②当CG是对角线时，
由中点公式得：12（2+94）=12（-14x2-12x+3），
整理得：x2+2x+5＝0，
∵△＜0，故该方程无解；
综上，点N的坐标为（﹣1+10，14）或（﹣1-10，14）或（﹣1+22，-14）或（﹣1﹣22，-14）．
如图1，抛物线y＝ax2+（a+3）x+3（a≠0）与x轴交于点A（4，0），与y轴交于点B，在x轴上有一动点E（m，0）（0＜m＜4），过点E作x轴的垂线交直线AB于点N，交抛物线于点P，过点P作PM⊥AB于点M．
（1）求a的值和直线AB的函数表达式；
（2）设△PMN的周长为C1，△AEN的周长为C2，若C1C2=65，求m的值；
（3）如图2，在（2）条件下，将线段OE绕点O逆时针旋转得到OE'，旋转角为α（0°＜α＜90°），连接E'A、E'B，求E'A+23E'B的最小值．
【解答】解：（1）令y＝0，则ax2+（a+3）x+3＝0，
∴（x+1）（ax+3）＝0，
∴x＝﹣1或-3a，
∵抛物线y＝ax2+（a+3）x+3（a≠0）与x轴交于点A（4，0），
∴-3a=4，
∴a=-34．
∵A（4，0），B（0，3），
设直线AB解析式为y＝kx+b，则b=34k+b=0，
解得k=-34b=3，
∴直线AB解析式为y=-34x+3；
（2）如图1，
∵PM⊥AB，PE⊥OA，
∴∠PMN＝∠AEN，
∵∠PNM＝∠ANE，
∴△PNM∽△ANE，
∴PNAN=65，
∵NE∥OB，
∴ANAB=AEOA，
∴AN=54（4﹣m），
∵抛物线解析式为y=-34x2+94x+3，
∴PN=-34m2+94m+3﹣（-34m+3）=-34m2+3m，
∴-34m2+3m54(4-m)=65，
解得m＝2或4，
经检验x＝4是分式方程的增根，
∴m＝2；
（3）如图2，在y轴上 取一点M′使得OM′=43，连接AM′，在AM′上取一点E′使得OE′＝OE．
∵OE′＝2，OM′•OB=43×3＝4，
∴OE′2＝OM′•OB，
∴OE'OM'=OBOE'，
∵∠BOE′＝∠M′OE′，
∴△M′OE′∽△E′OB，
∴ME'BE'=OE'OB=23，
∴M′E′=23BE′，
∴AE′+23BE′＝AE′+E′M′＝AM′，此时AE′+23BE′最小（两点间线段最短，A、M′、E′共线时），
最小值＝AM′=42+(43)2=4103．