

所属成套资源:2022年中考数学一轮复习知识点课标要求
专题训练15:反比例函数-2022年中考数学一轮复习知识点课标要求
展开
2022年中考数学一轮复习知识点课标要求专题训练15:反比例函数(含答案)
一、知识要点:
1、定义
一般的,形如 (是常数,k≠0)的函数叫做反比例函数。其它表示形式:或。
2、反比例函数的图象及其性质
反比例函数的图象是双曲线。当k>0时,双曲线的两支分别位于第一、第三象限,在每个象限内,y随x的增大而减小;当k<0时,双曲线的两支分别位于第二、第四象限,在每个象限内,y随x的增大而增大;
3、反比例函数与实际问题
在研究有关反比例函数的实际问题时,要遵循一审、二设、三列、四解的方法:
第1步:审题。认真读题,分析题中各个量之间的关系;
第2步:设自变量。根据各个量之间的关系设满足题意的自变量;
第3步:列函数。根据各个量之间的关系列出函数关系式;
第4步:求解。求出满足题意的数值。
二、课标要求:
1、结合具体情境体会反比例函数的意义,能根据已知条件确定反比例函数的表达式。
2、能画出反比例函数的图象,根据图象和表达式(k≠0)探索并理解k>0和k<0时,图象的变化情况。
3、能用反比例函数解决简单实际问题。
三、常见考点:
1、反比例函数的基本概念,根据已知条件写出或求出反比例函数解析式。
2、根据反比例函数的图象及性质解决相关问题,如不等式、图形面积等。
3、反比例函数与实际问题,反比例函数与综合问题。
四、专题训练:
1.已知点(x1,y1),(x2,y2)都在反比例函数y=的图象上,且0<x1<x2,则y1与y2的大小关系为( )
A.y1>y2 B.y1≥y2 C.y1<y2 D.y1≤y2
2.如图,在平面直角坐标系中,平行四边形OABC的顶点A在反比例函数y=上,顶点B在反比例函数y=上,点C在x轴的正半轴上,则平行四边形OABC的面积是( )
A. B.4 C.6 D.
3.如图,A、B是函数y=的图象上关于原点对称的任意两点,BC∥x轴,AC∥y轴,△ABC的面积记为S,则( )
A.S=2 B.S=4 C.2<S<4 D.S>4
4.如图,四边形OABC是矩形,四边形ADEF是边长为3的正方形,点A,D在x轴的正半轴上,点C在y轴的正半轴上,点F在AB上,点B、E在反比例函数y=(x>0)的图象上,且BF=5,则k值为( )
A.15 B. C. D.17
5.如图,矩形ABCD的顶点A、C分别在x、y轴的正半轴上,点D(﹣2,3),AD=5,若反比例函数y=(x>0)的图象经过点B,则k的值为( )
A.4 B. C.10 D.
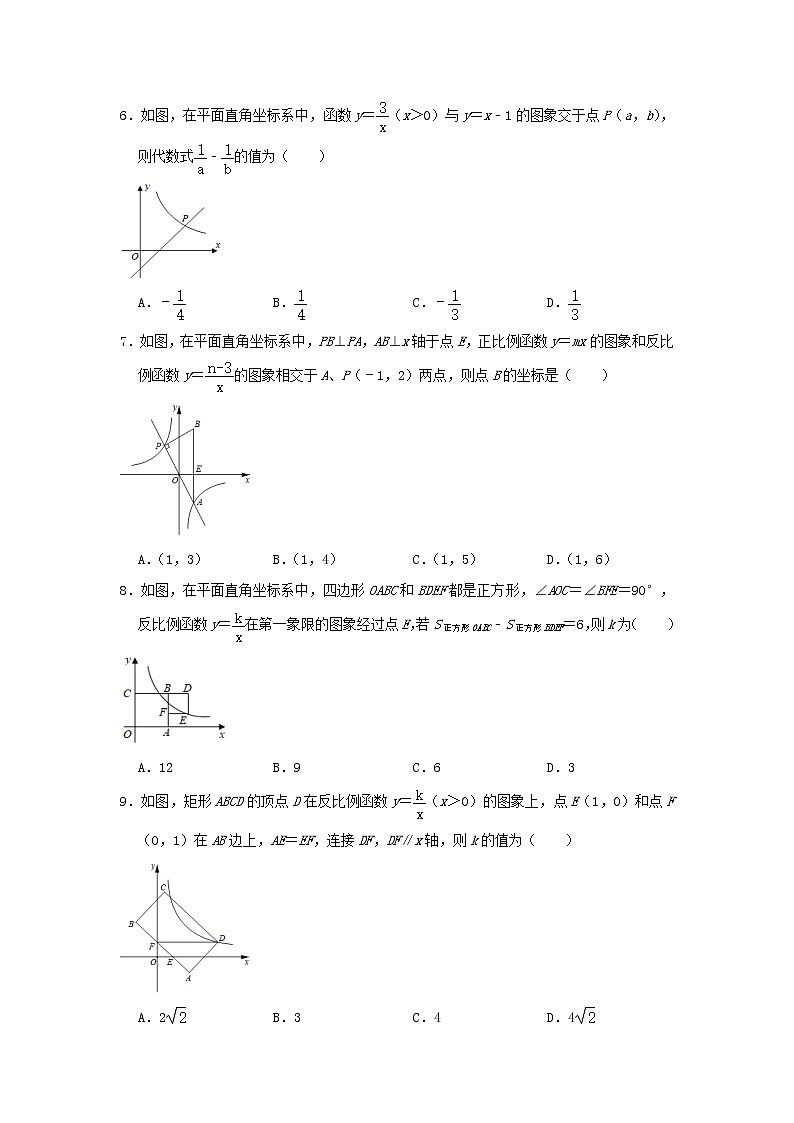
6.如图,在平面直角坐标系中,函数y=(x>0)与y=x﹣1的图象交于点P(a,b),则代数式﹣的值为( )
A.﹣ B. C.﹣ D.
7.如图,在平面直角坐标系中,PB⊥PA,AB⊥x轴于点E,正比例函数y=mx的图象和反比例函数y=的图象相交于A、P(﹣1,2)两点,则点B的坐标是( )
A.(1,3) B.(1,4) C.(1,5) D.(1,6)
8.如图,在平面直角坐标系中,四边形OABC和BDEF都是正方形,∠AOC=∠BFE=90°,反比例函数y=在第一象限的图象经过点E,若S正方形OABC﹣S正方形BDEF=6,则k为( )
A.12 B.9 C.6 D.3
9.如图,矩形ABCD的顶点D在反比例函数y=(x>0)的图象上,点E(1,0)和点F(0,1)在AB边上,AE=EF,连接DF,DF∥x轴,则k的值为( )
A.2 B.3 C.4 D.4
10.如图,点A,B是反比例函数y=(x>0)的图象上的两点,过点A作AC⊥x轴于点C,交直线OB于点D,连接OA.若点A的坐标为(3,1),OB=BD,则sin∠AOD= .
11.如图,直线y=x+4与x轴、y轴交于A、B两点,AC⊥AB,交双曲线y=(x<0)于C点,且BC交x轴于M点,BM=2CM,则k= .
12.如图,点A(﹣4,2)和B(2,﹣4)是一次函数y=kx+b的图象和反比例函数y=的图象的两个交点,则不等式kx+b<的解集是 .
13.如图,双曲线y=(x>0)经过矩形OABC的边AB,BC上的点F,E,其中CE=CB,AF=AB且四边形OEBF的面积为8,则k的值为 .
14.如图,反比例函数y=(k≠0)的图象经过A,B两点,过点A作AC⊥x轴,垂足为C,过点B作BD⊥x轴,垂足为D,连接AO,连接BO交AC于点E,若OC=CD,四边形BDCE的面积为3,则k的值为 .
15.在平面直角坐标系中,将一块直角三角板如图放置,直角顶点与原点O重合,顶点A,B恰好分别落在函数y=(x<0),y=(x>0)的图象上,若sin∠BAO=,则k的值为 .
16.如图,点A,D是反比例函数图象上的两个点,点B,C是反比例函数图象上的两个点,线段AB,CD均平行于y轴,若AB=1,CD=2,AB,CD之间的距离3,则m﹣n= .
17.如图,以矩形OABC的长OC作x轴,以宽OA作y轴建立平面直角坐标系,OA=4,OC=8,现作反比例函数交BC于点E,交AB于点F,沿EF折叠,点B落在OC的点G处,OG=3GC,则k的值是 .
18.如图,直线y=x与双曲线y=(k>0)交于A,B两点,BC⊥AB交该双曲线于点C,则sin∠BAC的值是 .
19.如图,在平面直角坐标系中,Rt△AOB的边OA在y轴上,OB在x轴上,反比例函数y=(k≠0)与斜边AB交于点C、D,连接OD,若AC:CD=1:2,S△OBD=,则k的值为 .
20.若函数y=与y=﹣2x﹣4的图象的交点坐标为(a,b),则的值是 .
21.如图,在直角坐标系中,已知点B(4,0),等边三角形OAB的顶点A在反比例函数y=的图象上,把△OAB向右平移a个单位长度,对应得到△O′A′B′当这个函数图象经过△O′A′B′一边的中点时,则a的值是 .
22.如图,一次函数y=x+b的图象与y轴交于点A,与反比例函数y=(x>0)的图象交于点B(2,6).
(1)求一次函数与反比例函数的关系式;
(2)C为线段AB延长线上一点,作CD∥OA与反比例函数y=(x>0)交于点D,连接OD,当四边形ACDO为平行四边形时,求点C的坐标.
23.如图,一次函数y=kx+b(k≠0)与反比例函数y=的图象的一支相交于点A,与x轴交于点B(﹣1,0),与y轴交于点C,已知AC=2BC.
(1)求一次函数的解析式;
(2)若反比例函数y=第一象限上有一点M,MN垂直于x轴,垂足为N,若△BOC∽△MNB,求点N的坐标.
24.已知一次函数y=kx+b与反比例函数y=的图象交于A(﹣3,2)、B(1,n)两点
(1)求一次函数和反比例函数的表达式;
(2)△AOB的面积为 ;
(3)直接写出不等式kx+b>的解集 ;
(4)点P在x的负半轴上,当△PAO为等腰三角形时,直接写出点P的坐标.
25.如图,已知A(﹣4,n),B(2,﹣4)是一次函数y=kx+b的图象和反比例函数y=的图象的两个交点.
(1)求反比例函数和一次函数的解析式;
(2)求△AOB的面积;
(3)求不等式kx+b﹣<0的解集(请直接写出答案).
26.一次函数y=kx+b的图象与反比例函数y=的图象交于点A(2,1)、B(﹣1,n)两点.
(1)求反比例函数的解析式;
(2)求一次函数的解析式;
(3)求△AOB的面积.
27.如图,直线y=﹣x+b分别与x轴,y轴相交于A,B,反比例函数y=(x>0)的图象与直线AB相交于C,D两点,且C点坐标是(2,n),tan∠BOC=.
(1)求直线AB及反比例函数的表达式.
(2)若x轴上有一点P,使∠ODP=90°,求P点的坐标.
参考答案
1.解:∵反比例函数y=中的k=5>0,
∴反比例函数y=的图象经过第一、三象限,且在每一象限内y的值随x的值增大而减小.
∵(x1,y1),(x2,y2),0<x1<x2,即这两点都位于第三象限,
∴y1>y2.
故选:A.
2.解:如图作BD⊥x轴于D,延长BA交y轴于E,
∵四边形OABC是平行四边形,
∴AB∥OC,OA=BC,
∴BE⊥y轴,
∴OE=BD,
∴Rt△AOE≌Rt△CBD(HL),
根据系数k的几何意义,S矩形BDOE=5,S△AOE=,
∴四边形OABC的面积=5﹣﹣=4,
故选:B.
3.解:设A点的坐标是(a,b),则根据函数的对称性得出B点的坐标是(﹣a,﹣b),则AC=2b,BC=2a,
∵A点在y=的图象上,
∴ab=1,
∴△ABC的面积S===2ab=2×1=2,
故选:A.
4.解:设AO=a,
∵四边形ADEF是边长为3的正方形,BF=5,
∴AB=8,OD=a+3,
∴B(a,8),E(a+3,3),
又∵点B、E在反比例函数y=(x>0)的图象上,
∴8a=3(a+3),
解得a=,
∴B(,8),
∴k=×8=,
故选:C.
5.解:设A(t,0),
∵D(﹣2,3),AD=5,
∴(t+2)2+32=52,解得t=2,
∴A(2,0),
设C(0,m),
∵D点向右平移2个单位,向上平移(m﹣3)个单位得到C点,
∴A点向右平移2个单位,向上平移(m﹣3)个单位得到B点,
∴B(4,m﹣3),
∵AC=BD,
∴22+m2=(4+2)2+(m﹣3﹣3)2,解得m=,
∴B(4,),
把B(4,)代入y=得k=4×=.
故选:D.
6.由题意得,函数y=(x>0)与y=x﹣1的图象交于点P(a,b),
∴ab=3,b=a﹣1,
∴﹣==﹣;
故选:C.
7.解:∵AP为正比例函数,故点A、P关于原点对称,则点A(1,﹣2),则设点B(1,t),
过点P作y轴的平行线交x轴于点N,交点B与x轴的平行线于点M,
∵∠MPB+∠NPO=90°,∠MPB+∠MBP=90°,
∴∠NPO=∠MPB,
BM=1﹣(﹣1)=2=PN=2,∠PNO=∠BMP=90°,
∴△PNO≌△BMP(AAS),
∴MP=ON=1,
故MN=MP+PN=1+2=3,
故点B的坐标为(1,3),
故选:A.
8.解:设正方形OABC、BDEF的边长分别为a和b,则D(a+b,a),E(a+b,a﹣b),
∵点E在反比例函数上,
∴(a+b)(a﹣b)=k,
∴a2﹣b2=k,
∵S正方形OABC﹣S正方形BDEF=a2﹣b2=6,
∴k=6
故选:C.
9.解:如图,过点D作DH⊥x轴于点H,设AD交x轴于点G,
∵DF∥x轴,
∴得矩形OFDH,
∴DF=OH,DH=OF,
∵E(1,0)和点F(0,1),
∴OE=OF=1,
∴∠OEF=45,
∴AE=EF=,
∵四边形ABCD是矩形,
∴∠A=90°,
∵∠AEG=∠OEF=45°,
∴AG=AE=,
∴EG=2,
∵DH=OF=1,
∠DHG=90°,∠DGH=∠AGE=45°,
∴GH=DH=1,
∴DF=OH=OE+EG+GH=1+2+1=4,
∴D(4,1),
∵矩形ABCD的顶点D在反比例函数y=(x>0)的图象上,
∵k=4.
则k的值为4.
故选:C.
10.解:∵AD⊥x轴,A(3,1),
∴OC=3,点D的横坐标为3,
将点A(3,1)代入反比例函数y=中得,k=3×1=3,
∴反比例函数的解析式为y=,
如图,过点B作BH⊥AD于H,
∵AD⊥x轴,
∴BH∥OC,
∵OB=BD,
∴CH=DH,
∴BH是△OCD的中位线,
∴BH=OC=,
当x=时,y==2,
∴点H(3,2),点B的坐标为(,2),
∴直线OB的解析式为y=x,
∴D(3,4),
∴OD=5,AD=3,
过点A作AG⊥OD于G,
∴S△AOD=AD•OC=OD•AG,
∴AG===,
∵OA==,
在Rt△AGO中,sin∠AOD===,
故答案为:.
11.解:作CD⊥OA于D,如图,
把x=0代入y=x+4得y=4,把y=0代入y=x+4得x+4=0,解得x=﹣8,
∴B点坐标为(0,4),A点坐标为(﹣8,0),即OB=4,OA=8,
∵CD⊥OA,
∴∠CDM=∠BOM=90°,
而∠CMD=∠BMO,
∴Rt△BMO∽Rt△CMD,
∴,
而BM=2CM,OB=4,
∴CD=2,
∵AC⊥AB,
∴∠BAO+∠CAD=90°,
而∠CAD+∠ACD=90°,
∴∠BAO=∠ACD,
∴Rt△BAO∽Rt△ACD,
∴,即,
∴AD=1,
∴OD=OA﹣DA=8﹣1=7,
∴C点坐标为(﹣7,﹣2),
把C(﹣7,﹣2)代入y=得k=14.
故答案为14.
12.解:由图象,得
x的取值范围是x>2或﹣4<x<0,
故答案为:x>2或﹣4<x<0.
13.解:设E(a,),F(b,),则a>0,b>0,
∴CE=a,AB=,OA=b,AF=,
∵AF=AB,
∴,即b=3a,
∴SOABC=OA•OB=b•==3k,
∵点E,F在双曲线上,
∴,
又∵四边形OEBF的面积为8,
S▱OABC=S△OCE+S△OAF+S▱OEBF,即3k=,
解得:k=4.
故答案为:4.
14.解:如图所示,
∵AC⊥x轴,BD⊥x轴,
∴BD∥AC,
∴△OCE∽△ODB,
∴=()2,
∵OC=CD,
∴=,
∵四边形BDCE的面积为3,
∴△ODB的面积为4,
∵点B在反比例函数y=的图象上,
∴k=﹣8.
故答案为:﹣8.
15.解:过点A、点B分别作AM⊥x轴,BN⊥x轴,垂足分别为M、N,
∵点A,B恰好分别落在函数y=(x<0),y=(x>0)的图象上,
∴S△AOM=|k|=﹣k,S△BON=|4|=2,
又∵sin∠BAO=,
∴=,
设OB=2k,则AB=5k,由勾股定理得,
OA===k,
又∵∠AOB=90°,
∴∠AOM+∠BON=180°﹣90°=90°,
∵∠AOM+∠MAO=90°,
∴∠MAO=∠BON,
又∵∠AMO=∠BNO=90°,
∴△AOM∽△OBN,
∴=()2,
∴=()2=,
∴k=﹣1,
故答案为:﹣1.
16.解:设AB与x轴交于点E,CD与x轴相交于点F,连接OA、OB、OC、OD,
∵点A,D是反比例函数图象上的两个点,点B,C是反比例函数图象上的两个点,
∴S△AOE=S△DOF=|n|=﹣n,
S△BOE=S△COF=|m|=m,
∵S△AOB=S△AOE+S△BOE,
∴AB•OE=m﹣n,
∵AB=1,
∴OE=m﹣n,
同理,OF=m﹣n,
又∵线段AB,CD均平行于y轴且AB,CD之间的距离3,
∴OE+OF=3,
即(m﹣n)+(m﹣n)=3,
∴m﹣n=2,
故答案为:2.
17.解:由折叠得,EG=EB,
∵OC=8,OG=3GC,
∴OG=8×=6,GC=8×=2,
设EC=x,则EB=EG=4﹣x,
在Rt△EGC中,由勾股定理得,
(4﹣x)2=x2+22,
解得x=,
∴E(8,),
把E(8,)代入反比例函数关系式得,
k=8×=12,
故答案为:12.
18.解:∵与交于A、B两点,
∴联立方程组,
解得,,
∴,
∴AB的长为,
设直线BC的解析式为y=mx+b,
∵BC⊥AB,
∴m=﹣2,
∴b=﹣,
∴,
联立,
解得,,
∴BC=,
由勾股定理得,AC=,
∴.
故答案为:.
19.解:设D(m,n),过点C作CE⊥y轴于点E,过点D作DF⊥y轴于点F.则k=mn,
∴△ACE∽△ADF,
∵AC:CD=1:2,
∴AC:AD=1:3,
∴,
∴CE=DF=m,
当x=m时,y=,
∴C(m,3n),
∵D(m,n),
∴直线AB的表达式为y=﹣,
∴B(,0),OB=,
∵S△OBD=,
∴,
∴mn=,
∴k=mn=,
故答案为.
20.解:联立两个函数表达式得,
整理得:x2+2x+1=0,
解得:x=﹣1,
∴y=﹣2,
交点坐标是(﹣1,﹣2),
∴a=﹣1,b=﹣2,
则=﹣1﹣1=﹣2.
故答案为﹣2.
21.解:如图,过点A作AC⊥OB,垂足为C,设OA的中点为M,AB的中点为N,
∵点B(4,0),等边三角形OAB,
∴OC=BC=2,OA=OB=AB=4,
∴AC==2,
∴A(2,2),
∴k=2×2=4,
∴反比例函数关系式为y=,
∵O(0,0),A(2,2),B(4,0),
∴M(1,),N(3,),
当y=时,x==4,
∴a=4﹣1=3或a=4﹣3=1,
故答案为:3或1.
22.解:(1)∵点B(2,6)在直线y=x+b上,
∴2+b=6,
∴b=4,
∴一次函数的解析式为y=x+4;
∵点B(2,6)在反比例函数y=(x>0)的图象上,
∴k=2×6=12,
∴反比例函数的解析式为y=;
(2)由(1)知,一次函数的解析式为y=x+4,
∴A(0,4),
∴OA=4,
∵四边形ACDO为平行四边形,
∴CD=OA=4,
设点C的坐标为(m,m+4)(m>2),
∵CD∥OA,
∴D(m,),
∴CD=m+4﹣,
∴m+4﹣=4,
∴m=2或m=﹣2(舍),
∴C(2,2+4).
23.解:(1)如图,
过点A作AH⊥x轴于H,
∴AH∥OC,
∴△BOC∽△BHA,
∴,
∵AC=2BC,
∴=,
∵B(﹣1,0),
∴OB=1,
∴,
∴BH=3,
∴OH=2,
∴点A的横坐标为2,
∵点A在反比例函数y=的图象上,
∴点A的纵坐标为6,
∴A(2,6),
∴,
∴,
∴一次函数的解析式为y=2x+2;
(2)由(1)知,直线AB的解析式为y=2x+2,
∴C(0,2),
∴OC=2,
设点M(m,),
∵MN⊥x轴,
∴N(m,0),
∴BN=m+1,MN=,
∵△BOC∽△MNB,
∴,
∴,
∴m=(舍)或m=,
∴N(,0).
24.解:(1)∵反比例函数y=经过点A(﹣3,2),
∴m=﹣6,
∵点B(1,n)在反比例函数图象上,
∴n=﹣6.
∴B(1,﹣6),
把A,B的坐标代入y=kx+b,则,解得,
∴一次函数的解析式为y=﹣2x﹣4,反比例函数的解析式为y=﹣;
(2)如图设直线AB交y轴于C,则C(0,﹣4),
∴S△AOB=S△OCA+S△OCB=×4×3+×4×1=8,
故答案为8;
(3)观察函数图象知,kx+b>的解集为0<x<1或x<﹣3,
故答案为0<x<1或x<﹣3;
(4)由题意OA==,
当AO=AP时,可得P1(﹣6,0),
当OA=OP时,可得P2(﹣,0),P4(,0)(舍去),
当PA=PO时,过点A作AJ⊥x轴于J.设OP3=P3A=x,
在Rt△AJP3中,则有x2=22+(3﹣x)2,
解得x=,
∴P3(﹣,0),
综上所述,满足条件的点P的坐标为(﹣,0)或(﹣,0)或(﹣6,0).
25.解:(1)把B(2,﹣4)代入y=得m=2×(﹣4)=﹣8,
所以反比例函数解析式为y=﹣,
把A(﹣4,n)代入y=﹣得﹣4n=﹣8,解得n=2,则A点坐标为(﹣4,2),
把A(﹣4,2)、B(2,﹣4)代入y=kx+b得,解得,
所以一次函数解析式为y=﹣x﹣2;
(2)把y=0代入y=﹣x﹣2得﹣x﹣2=0,解得x=﹣2,则C点坐标为(﹣2,0),
所以S△AOB=S△AOC+S△BOC=×2×2+×2×4=6;
(3)﹣4<x<0或x>2.
26.解:(1)因为经过A(2,1),所以m=2.
所以反比例函数的解析式为y=.
(2)因为B(﹣1,n)在y=上,所以n=﹣2.
所以B的坐标是(﹣1,﹣2).
把A(2,1)、B(﹣1,﹣2)代入y=kx+b.得:
,
解得,
所以y=x﹣1.
(3)设直线y=x﹣1与坐标轴分别交于C、D,则C(1,0)、D(0,﹣1).
所以:S△AOB=S△BOD+S△COD+S△AOC=×1×1+×1×1+×1×1=.
27.解:(1)如图1,
过点C作CE⊥OB于E,
∴∠OEC=90°,
∵C(2,n),
∴CE=2,OE=n,
∵tan∠BOC=,
∴,
∴=,
∴n=4,
∴C(2,4),
将点C的坐标代入直线AB:y=﹣x+b中,得4=﹣×2+b,
∴b=5,
∴直线AB的解析式为y=﹣x+5,
将点C的坐标代入反比例函数y=中,得k=2×4=8,
∴反比例函数的解析式为y=;
(2)如图2,由(1)知,直线AB的解析式为y=﹣x+5①,
反比例函数的解析式为y=②,
联立①②解得,或,
∴D(8,2),
过点D作DF⊥OA于F,
∴∠OFD=90°,
∴∠DOF+∠ODF=90°,
∵∠ODP=90°,
∴∠ODP+∠PDF=90°,
∴∠DOF=∠PDF,
∴△OFD∽△DFP,
∴,
∵D(8,2),
∴OF=8,DF=2,
∴,
∴PF=,
∴OP=OF+PF=8+=,
∴P(,0).






