专题4.1 相似三角形的六大证明技巧（1）-2021年中考数学第二轮总复习课件（全国通用）

这是一份专题4.1 相似三角形的六大证明技巧（1）-2021年中考数学第二轮总复习课件（全国通用），共23页。PPT课件主要包含了三点定型法，等线段代换法，等比代换法，温故知新2分钟，adbc，AB∥CD，△PAB∽△PDC，△AOB∽△COD，AD∥BC，OB2OE·OF等内容，欢迎下载使用。
通过前面的学习,我们知道,比例线段的证明,离不开“平行线模型”(A型、X型、K型等),也离不开下面的6种“相似模型”。 “模型”只是工具,怎样选择工具,怎样使用工具,取决于我们如何思考问题.合理的思维方法,能让模型成为解题的利刃,让复杂的问题变简单。 【技巧一】三点定型 【技巧四】等积代换 【技巧二】等线段代换 【技巧五】证等量先证等比 【技巧三】等比代换 【技巧六】几何计算
1.比例的基本性质：
2.更比定理：
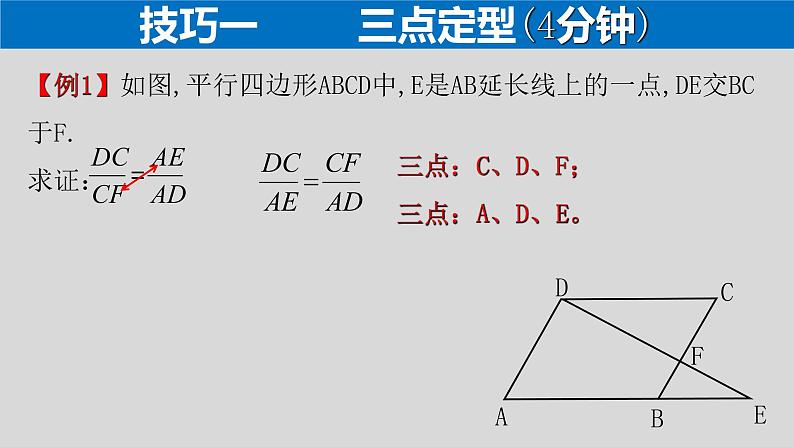
技巧一 三点定型(4分钟)
三点：C、D、F； 三点：A、D、E。
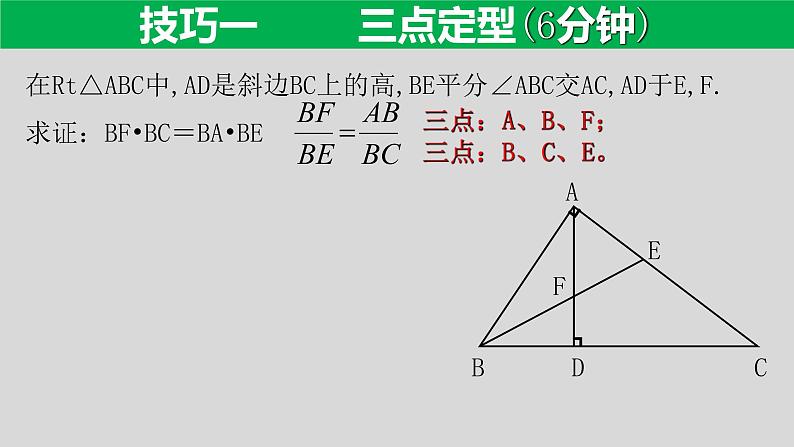
技巧一 三点定型(6分钟)
在Rt△ABC中,AD是斜边BC上的高,BE平分∠ABC交AC,AD于E,F.求证：BF•BC＝BA•BE
三点：A、B、F； 三点：B、C、E。
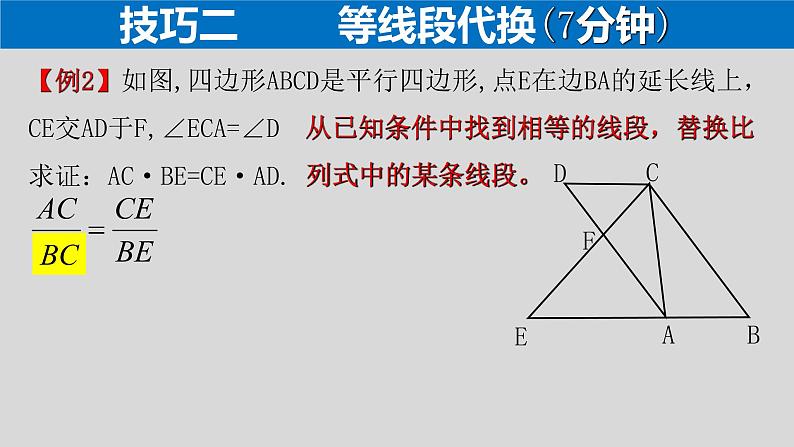
【例2】如图,四边形ABCD是平行四边形,点E在边BA的延长线上，CE交AD于F,∠ECA=∠D求证：AC·BE=CE·AD.
从已知条件中找到相等的线段，替换比列式中的某条线段。
技巧二 等线段代换(7分钟)
如图,在△ABC中,AD平分∠BAC,AD的垂直平分线交AD于E,交BC的延长线于F.求证：FD2=FB·FC.
技巧三 等比代换(7分钟)
【例3】如图,已知AB∥CD,AC、BD相交于点O.求证：OA•PD=OC•PA
OA•PD=OC•PA
1.如图,在△ABC中,点D在BC边上,连接AD,点G在AD上,GE∥BD,交AB于点E,GF∥AC,交CD于点F,则下列结论一定成立的是( ) A. B. C. D.
2.如图,□ABCD中,过B作直线AC、AD于O、E,交CD的延长线于F,求证：OB2=OE·OF.
比例线段的证明,离不开“平行线模型”(K型、A型、X型等),也离不开6种“相似模型”。
本节课我们学习了相似三角形的6大证明技巧中的哪3种？
我们学习了①三点定型法；②等线段代换；③等比代换。
“模型”只是工具,怎样选择工具,怎样使用工具,取决于我们如何思考问题.合理的思维方法,能让模型成为解题的利刃,让复杂的问题变简单。
1.如图,△ABC中,∠BAC=90º,M为BC的中点,DM⊥BC交CA的延长线于D,交AB于E.求证：AM2=MD·ME.
2.如图,△ABC中,AB=AC,AD是中线,P是AD上一点,过C作CF∥AB,延长BP交AC于E,交CF于G.求证：BP2=PE·PF.
3.如图,△ABC是等腰三角形,AB=AC,∠BAC=90º,∠DAE=45º,求证：(1)AB2=BE·CD；(2)BD2+EC2=DE2。
1.如图,在△ABC中(AB＞AC)的边AB上取一点D,在边AC上取一点E,使AD=AE,直线DE和BC的延长线交于点P.求证：BP·CE=CP·BD
过点B作BF∥AC交PD的延长线于点F.则BF=BD
2.(大练P1017)如图，在△ABC中，AB=AC,以AB为直径的⊙O交AC于点E，交BC于点D.求证：(1)点D是BC的中点；(2)△BEC∽△ADC；(3)BC2=2AB•CE
4.如图,在△ABC中，已知∠A=90º时，AD⊥BC于D,E为直角边AC的中点，过D、E作直线交AB的延长线于F.求证：AB·AF=AC·DF.