专题二 图形规律-2022年中考数学二轮复习之重难热点提分专题

这是一份专题二 图形规律-2022年中考数学二轮复习之重难热点提分专题，文件包含专题二图形规律-2022年中考数学二轮复习之重难热点提分专题解析版docx、专题二图形规律-2022年中考数学二轮复习之重难热点提分专题原卷版docx等2份试卷配套教学资源，其中试卷共22页， 欢迎下载使用。

专题二 图形规律
题型一：动点图形规律
1．（2021常德）如图，将一枚跳棋放在七边形ABCDEFG的顶点A处，按顺时针方向移动这枚跳棋2021次．移动规则是：第k次移动k个顶点（如第一次移动1个顶点，跳棋停留在B处，第二次移动2个顶点，跳棋停留在D处），按这样的规则，在这2021次移动中，跳棋不可能停留的顶点是（　　）

A．C、E B．E、F C．G、C、E D．E、C、F
【分析】设顶点A，B，C，D，E，F，G分别是第0，1，2，3，4，5，6格，因棋子移动了k次后走过的总格数是1+2+3+…+k=12k（k+1），然后根据题目中所给的第k次依次移动k个顶点的规则，可得到不等式最后求得解．
【解析】经实验或按下方法可求得顶点C，E和F棋子不可能停到．
设顶点A，B，C，D，E，F，G分别是第0，1，2，3，4，5，6格，
因棋子移动了k次后走过的总格数是1+2+3+…+k=12k（k+1），应停在第12k（k+1）﹣7p格，
这时P是整数，且使0≤12k（k+1）﹣7p≤6，分别取k＝1，2，3，4，5，6，7时，
12k（k+1）﹣7p＝1，3，6，3，1，0，0，发现第2，4，5格没有停棋，
若7＜k≤2021，
设k＝7+t（t＝1，2，3）代入可得，12k（k+1）﹣7p＝7m+12t（t+1），
由此可知，停棋的情形与k＝t时相同，
故第2，4，5格没有停棋，即顶点C，E和F棋子不可能停到．
故选：D．
题型二：几何图形规律
2．（2021烟台）如图，△OA1A2为等腰直角三角形，OA1＝1，以斜边OA2为直角边作等腰直角三角形OA2A3，再以OA3为直角边作等腰直角三角形OA3A4，…，按此规律作下去，则OAn的长度为（　　）

A．（）n B．（）n﹣1 C．（）n D．（）n﹣1
【分析】利用等腰直角三角形的性质以及勾股定理分别求出各边长，依据规律即可得出答案．
【解析】∵△OA1A2为等腰直角三角形，OA1＝1，
∴OA2=2；
∵△OA2A3为等腰直角三角形，
∴OA3＝2=(2)2；
∵△OA3A4为等腰直角三角形，
∴OA4＝22=(2)3．
∵△OA4A5为等腰直角三角形，
∴OA5＝4=(2)4，
……
∴OAn的长度为（2）n﹣1．
故选：B．
3．（2021盐城）把1～9这9个数填入3×3方格中，使其任意一行，任意一列及两条对角线上的数之和都相等，这样便构成了一个“九宫格”．它源于我国古代的“洛書”（图①），是世界上最早的“幻方”．图②是仅可以看到部分数值的“九宫格”，则其中x的值为（　　）

A．1 B．3 C．4 D．6
【分析】根据任意一行，任意一列及两条对角线上的数之和都相等，可得第三行与第三列上的两个数之和相等，依此列出方程即可．
【解析】由题意，可得8+x＝2+7，
解得x＝1．
故选：A．
4．（2021•成都）如图，六边形ABCDEF是正六边形，曲线FA1B1C1D1E1F1…叫做“正六边形的渐开线”，FA1，A1B1，B1C1，C1D1，D1E1，E1F1，…的圆心依次按A，B，C，D，E，F循环，且每段弧所对的圆心角均为正六边形的一个外角．当AB＝1时，曲线FA1B1C1D1E1F1的长度是　 　．

【分析】利用弧长公式计算即可解决问题．
【解析】FA1的长=60⋅π⋅1180=π3，
A1B1的长=60⋅π⋅2180=2π3，
B1C1的长=60⋅π⋅3180=3π3，
C1D1的长=60⋅π⋅4180=4π3，
D1E1的长=60⋅π⋅5180=5π3，
E1F1的长=60⋅π⋅6180=6π3，
∴曲线FA1B1C1D1E1F1的长度=π3+2π3+⋯+6π3=21π3=7π，
故答案为7π．
5．（2021•湘西州）观察下列结论：
（1）如图①，在正三角形ABC中，点M，N是AB，BC上的点，且AM＝BN，则AN＝CM，∠NOC＝60°；
（2）如图2，在正方形ABCD中，点M，N是AB，BC上的点，且AM＝BN，则AN＝DM，∠NOD＝90°；
（3）如图③，在正五边形ABCDE中点M，N是AB，BC上的点，且AM＝BN，则AN＝EM，∠NOE＝108°；
…
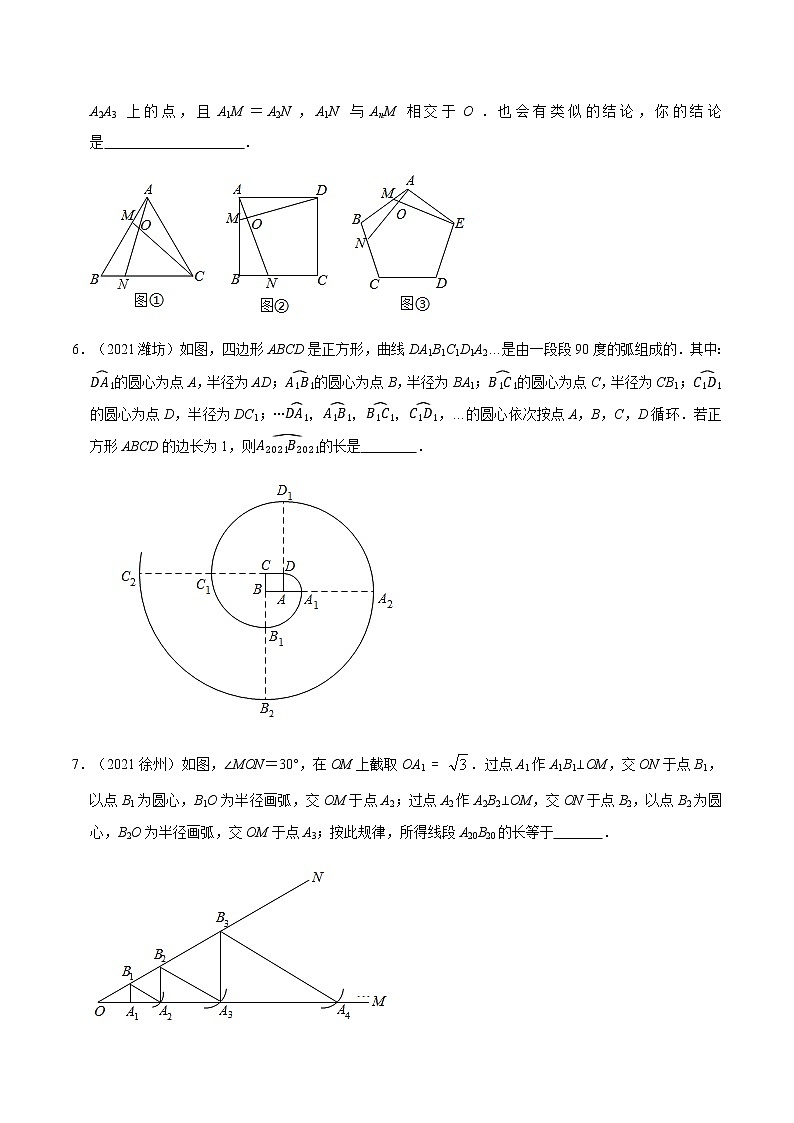
根据以上规律，在正n边形A1A2A3A4…An中，对相邻的三边实施同样的操作过程，即点M，N是A1A2，A2A3上的点，且A1M＝A2N，A1N与AnM相交于O．也会有类似的结论，你的结论是　 　．

【分析】根据已知所给得到规律，进而可得在正n边形A1A2A3A4…An中，对相邻的三边实施同样的操作过程会有类似的结论．
【解析】∵（1）如图①，在正三角形ABC中，点M，N是AB，BC上的点，且AM＝BN，则AN＝CM，∠NOC=(3-2)×180°3=60°；
（2）如图2，在正方形ABCD中，点M，N是AB，BC上的点，且AM＝BN，则AN＝DM，∠NOD=(4-2)×180°4=90°；
（3）如图③，在正五边形ABCDE中点M，N是AB，BC上的点，且AM＝BN，则AN＝EM，∠NOE=(5-2)×180°5=108°；
…
根据以上规律，在正n边形A1A2A3A4…An中，
对相邻的三边实施同样的操作过程，即点M，N是A1A2，A2A3上的点，
且A1M＝A2N，A1N与AnM相交于O．
也有类似的结论是A1N＝AnM，∠NOAn=(n-2)×180°n．
故答案为：A1N＝AnM，∠NOAn=(n-2)×180°n．
6．（2021潍坊）如图，四边形ABCD是正方形，曲线DA1B1C1D1A2…是由一段段90度的弧组成的．其中：DA1的圆心为点A，半径为AD；A1B1的圆心为点B，半径为BA1；B1C1的圆心为点C，半径为CB1；C1D1的圆心为点D，半径为DC1；⋯DA1，A1B1，B1C1，C1D1，…的圆心依次按点A，B，C，D循环．若正方形ABCD的边长为1，则A2021B2021的长是　 　．

【分析】曲线DA1B1C1D1A2…是由一段段90度的弧组成的，半径每次比前一段弧半径+1，到ADn﹣1＝AAn＝4（n﹣1）+1，BAn＝BBn＝4（n﹣1）+2，再计算弧长．
【解析】由图可知，曲线DA1B1C1D1A2…是由一段段90度的弧组成的，半径每次比前一段弧半径+1，AD＝AA1＝1，BA1＝BB1＝2，……，ADn﹣1＝AAn＝4（n﹣1）+1，BAn＝BBn＝4（n﹣1）+2，
故A2021B2021的半径为BA2021＝BB2021＝4（2021﹣1）+2＝8078，A2021B2021的弧长=90180×8078π=4039π．
故答案为：4039π．
7．（2021徐州）如图，∠MON＝30°，在OM上截取OA1=．过点A1作A1B1⊥OM，交ON于点B1，以点B1为圆心，B1O为半径画弧，交OM于点A2；过点A2作A2B2⊥OM，交ON于点B2，以点B2为圆心，B2O为半径画弧，交OM于点A3；按此规律，所得线段A20B20的长等于　 　．

【分析】利用三角形中位线定理证明A2B2＝2A1B1，A3B3＝2A2B2＝22•A1B1，寻找规律解决问题即可．
【解析】∵B1O＝B1A1，B1A1⊥OA2，
∴OA1＝A1A2，
∵B2A2⊥OM，B1A1⊥OM，
∴B1A1∥B2A2，
∴B1A1=12A2B2，
∴A2B2＝2A1B1，
同法可得A3B3＝2A2B2＝22•A1B1，…，
由此规律可得A20B20＝219•A1B1，
∵A1B1＝OA1•tan30°=3×33=1，
∴A20B20＝219，
故答案为219．
8．（2021辽阳）如图，四边形ABCD是矩形，延长DA到点E，使AE＝DA，连接EB，点F1是CD的中点，连接EF1，BF1，得到△EF1B；点F2是CF1的中点，连接EF2，BF2，得到△EF2B；点F3是CF2的中点，连接EF3，BF3，得到△EF3B；…；按照此规律继续进行下去，若矩形ABCD的面积等于2，则△EFnB的面积为　 　．（用含正整数n的式子表示）

【分析】先求得△EF1D的面积为1，再根据等高的三角形面积比等于底边的比可得EF1F2的面积，EF2F3的面积，…，EFn﹣1Fn的面积，以及△BCFn的面积，再根据面积的和差关系即可求解．
【解析】∵AE＝DA，点F1是CD的中点，矩形ABCD的面积等于2，
∴△EF1D和△EAB的面积都等于1，
∵点F2是CF1的中点，
∴△EF1F2的面积等于12，
同理可得△EFn﹣1Fn的面积为12n-1，
∵△BCFn的面积为2×12n÷2=12n，
∴△EFnB的面积为2+1﹣1-12-⋯-12n-1-12n=2﹣（1-12n）=2n+12n．
故答案为：2n+12n．

题型三：几何函数图形规律
9．（2021荆门）在平面直角坐标系xOy中，Rt△AOB的直角顶点B在y轴上，点A的坐标为（1，），将Rt△AOB沿直线y＝﹣x翻折，得到Rt△A'OB'，过A'作A'C垂直于OA'交y轴于点C，则点C的坐标为（　　）

A．（0，﹣2） B．（0，﹣3） C．（0，﹣4） D．（0，﹣4）
【分析】依据轴对称的性质可得OB'＝OB=3，A′B′＝AB＝1，OA′＝OA＝2，进而通过证得△A′OB′∽△COA′，求得OC＝4，即可证得C的坐标为（0，﹣4）．
【解析】∵点A的坐标为（1，3），
∴AB＝1，OB=3，
∴OA=AB2+OB2=12+(3)2=2，
∵将Rt△AOB沿直线y＝﹣x翻折，得到Rt△A'OB'，
∴OB'＝OB=3，A′B′＝AB＝1，OA′＝OA＝2，
∴A'（-3，﹣1），
∵过A'作A'C垂直于OA'交y轴于点C，
∴∠A′OC+∠A′CO＝90°，
∵∠A′OB′+∠A′OC＝90°，
∴∠A′CO＝∠A′OB′，
∵∠A′B′O＝∠OA′C＝90°，
∴△A′OB′∽△COA′，
∴OCOA'=OA'A'B'，即OC2=21，
∴OC＝4，
∴C（0，﹣4），
故选：C．
10．（2021鄂州）如图，点A1，A2，A3…在反比例函数y=（x＞0）的图象上，点B1，B2，B3，…Bn在y轴上，且∠B1OA1＝∠B2B1A2＝∠B3B2A3＝…，直线y＝x与双曲线y=交于点A1，B1A1⊥OA1，B2A2⊥B1A2，B3A3⊥B2A3…，则Bn（n为正整数）的坐标是（　　）

A．（2，0） B．（0，）
C．（0，） D．（0，2）
【分析】由题意，△OA1B1，△B1A2B2，△B2A3B3，…，都是等腰直角三角形，想办法求出OB1，OB2，OB3，OB4，…，探究规律，利用规律解决问题即可得出结论．
【解析】由题意，△OA1B1，△B1A2B2，△B2A3B3，…，都是等腰直角三角形，
∵A1（1，1），
∴OB1＝2，设A2（m，2+m），
则有m（2+m）＝1，
解得m=2-1，
∴OB2＝22，
设A3（a，22+n），则有n＝a（22+a）＝1，
解得a=3-2，
∴OB3＝23，
同法可得，OB4＝24，
∴OBn＝2n，
∴Bn（0，2n）．
故选：D．
11．（2021温州）点P，Q，R在反比例函数y=（常数k＞0，x＞0）图象上的位置如图所示，分别过这三个点作x轴、y轴的平行线．图中所构成的阴影部分面积从左到右依次为S1，S2，S3．若OE＝ED＝DC，S1+S3＝27，则S2的值为 　．

【分析】设CD＝DE＝OE＝a，则P（k3a，3a），Q（k2a，2a），R（ka，a），推出CP=3k3a，DQ=k2a，ER=ka，推出OG＝AG，OF＝2FG，OF=23GA，推出S1=23S3＝2S2，根据S1+S3＝27，求出S1，S3，S2即可．
【解析】∵CD＝DE＝OE，
∴可以假设CD＝DE＝OE＝a，
则P（k3a，3a），Q（k2a，2a），R（ka，a），
∴CP=k3a，DQ=k2a，ER=ka，
∴OG＝AG，OF＝2FG，OF=23GA，
∴S1=23S3＝2S2，
∵S1+S3＝27，
∴S3=815，S1=545，S2=275，
故答案为275．
12．（2021•自贡）如图，直线y=与y轴交于点A，与双曲线y=在第三象限交于B、C两点，且AB•AC＝16．下列等边三角形△OD1E1，△E1D2E2，△E2D3E3，…的边OE1，E1E2，E2E3，…在x轴上，顶点D1，D2，D3，…在该双曲线第一象限的分支上，则k＝　 　，前25个等边三角形的周长之和为　 ．

【分析】设直线y=-3x+b与x轴交于点D，作BE⊥y轴于E，CF⊥y轴于F．首先证明∠ADO＝60°，可得AB＝2BE，AC＝2CF，由直线y=-3x+b与双曲线y=kx在第一象限交于点B、C两点，可得-3x+b=kx，整理得，-3x2+bx﹣k＝0，由韦达定理得：x1x2=33k，即EB•FC=33k，由此构建方程求出k即可，第二个问题分别求出第一个，第二个，第三个，第四个三角形的周长，探究规律后解决问题．
【解析】设直线y=-3x+b与x轴交于点D，作BE⊥y轴于E，CF⊥y轴于F．
∵y=-3x+b，
∴当y＝0时，x=33b，即点D的坐标为（33b，0），
当x＝0时，y＝b，即A点坐标为（0，b），
∴OA＝﹣b，OD=-33b．
∵在Rt△AOD中，tan∠ADO=OAOD=3，
∴∠ADO＝60°．
∵直线y=-3x+b与双曲线y=kx在第三象限交于B、C两点，
∴-3x+b=kx，
整理得，-3x2+bx﹣k＝0，
由韦达定理得：x1x2=33k，即EB•FC=33k，
∵EBAB=cos60°=12，
∴AB＝2EB，
同理可得：AC＝2FC，
∴AB•AC＝（2EB）（2FC）＝4EB•FC=433k＝16，
解得：k＝43．
由题意可以假设D1（m，m3），
∴m2•3=43，
∴m＝2
∴OE1＝4，即第一个三角形的周长为12，
设D2（4+n，3n），
∵（4+n）•3n＝43，
解得n＝22-2，
∴E1E2＝42-4，即第二个三角形的周长为122-12，
设D3（42+a，3a），
由题意（42+a）•3a＝43，
解得a＝23-22，即第三个三角形的周长为123-122，
…，
∴第四个三角形的周长为124-123，
∴前25个等边三角形的周长之和12+122-12+123-122+124-123+⋯+1225-1224=1225=60，
故答案为43，60．

13．（2021齐齐哈尔）如图，在平面直角坐标系中，等腰直角三角形①沿x轴正半轴滚动并且按一定规律变换，每次变换后得到的图形仍是等腰直角三角形．第一次滚动后点A1（0，2）变换到点A2（6，0），得到等腰直角三角形②；第二次滚动后点A2变换到点A3（6，0），得到等腰直角三角形③；第三次滚动后点A3变换到点A4（10，），得到等腰直角三角形④；第四次滚动后点A4变换到点A5（10+，0），得到等腰直角三角形⑤；依此规律…，则第2021个等腰直角三角形的面积是　 　．

【分析】根据A1（0，2）确定第1个等腰直角三角形（即等腰直角三角形①）的面积，根据A2（6，0）确定第1个等腰直角三角形（即等腰直角三角形②）的面积，…，同理，确定规律可得结论．
【解析】∵点A1（0，2），
∴第1个等腰直角三角形的面积=12×2×2=2，
∵A2（6，0），
∴第2个等腰直角三角形的边长为6-22=22，
∴第2个等腰直角三角形的面积=12×22×22=4＝22，
∵A4（10，42），
∴第3个等腰直角三角形的边长为10﹣6＝4，
∴第3个等腰直角三角形的面积=12×4×4=8＝23，
…
则第2021个等腰直角三角形的面积是22021；
故答案为：22021（形式可以不同，正确即得分）．