
初中数学鲁教版 (五四制)八年级下册5 相似三角形判定定理的证明随堂练习题
展开
这是一份初中数学鲁教版 (五四制)八年级下册5 相似三角形判定定理的证明随堂练习题,共14页。
知识能力全练
知识点一 相似三角形的有关概念
1.如图所示,△ADE∽△ABC,若AD=1,BD=2,则△ADE与△ABC的相似比是( )
A.1:2 B.1:3 C.2:3 D.3:2
2.在△ABC和△ABC中,AB=AC,A´B´=A´C´,若添加一个条件可使两个三角形相似,甲添加的条件是∠A=∠A´=60°;乙添加的条件是∠A=∠A´=90°对于甲、乙添加的条件判断正确的是( )
A.甲对乙错 B.甲错乙对 C.两人都对 D.两人都错
知识点二 相似三角形的判定定理1
3.如图所示,已知△ABC与△BDE都是等边三角形,点D在边AC上(不与点A、C重合),DE与AB相交于点F,那么与△BFD相似的三角形是( )
A.△BFE B.△BDC C.△BDA D.△AFD
4.如图所示,在△ABC中,DE∥BC,∠B=∠ACD,则图中相似三角形有( )
A.2对 B.3对 C.4对 D.5对
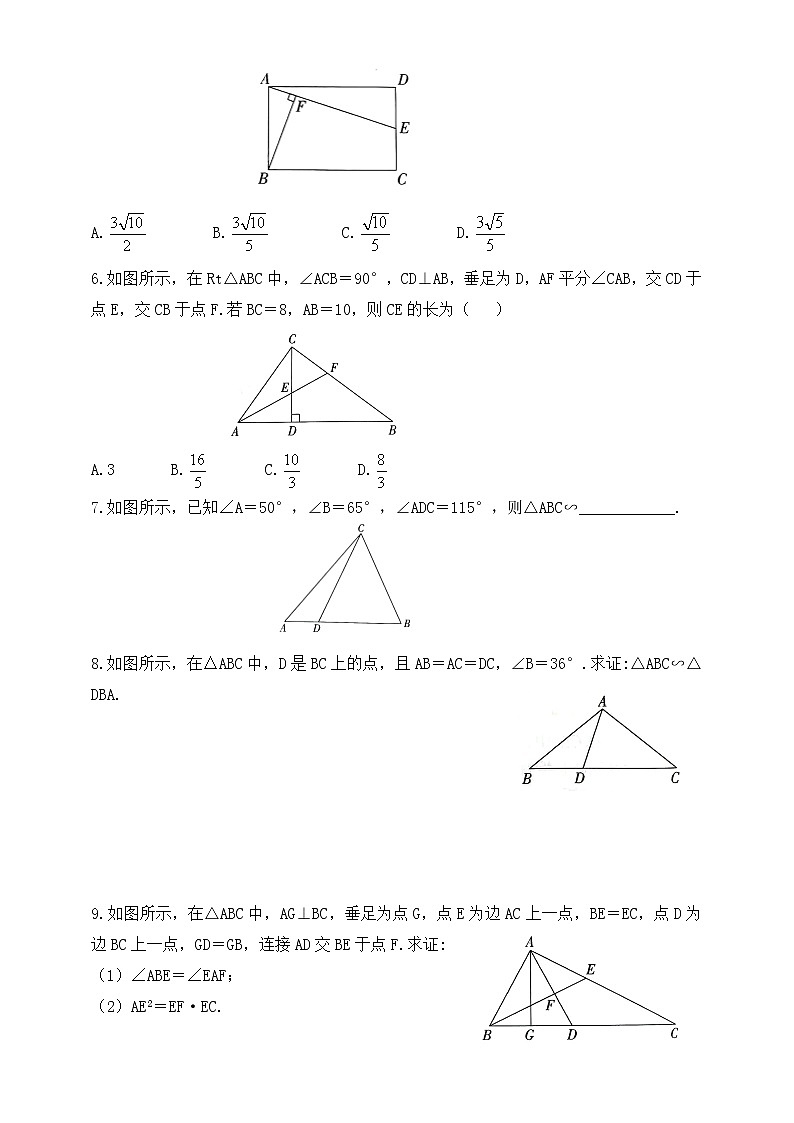
5.如图所示,在矩形ABCD中,AB=2,BC=3,若点E是边CD的中点,连接AE,过点B作BF⊥AE于点F,则BF的长为( )
A. B. C. D.
6.如图所示,在Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为D,AF平分∠CAB,交CD于点E,交CB于点F.若BC=8,AB=10,则CE的长为( )
A.3 B. C. D.
7.如图所示,已知∠A=50°,∠B=65°,∠ADC=115°,则△ABC∽____________.
8.如图所示,在△ABC中,D是BC上的点,且AB=AC=DC,∠B=36°.求证:△ABC∽△DBA.
9.如图所示,在△ABC中,AG⊥BC,垂足为点G,点E为边AC上一点,BE=EC,点D为边BC上一点,GD=GB,连接AD交BE于点F.求证:
(1)∠ABE=∠EAF;
(2)AE2=EF·EC.
知识点三 相似三角形的判定定理2
10.如图所示,△ABC的顶点都在小正方形的顶点上,则与△ABC相似的阴影三角形为
( )
11.如图所示,∠1=∠2,要使△ABC∽△ADE,只需要添加一个条件即可,这个条件不可能是( )
A.∠B=∠D B.∠C=∠E C. D.
12.如图所示,已知OA=20,OB=30,OD=22,OC=33,AB=24,则CD的长是( )
A. B. C. D.
13.如图所示,把△ABC绕点A旋转得到△ADE,当点D刚好落在BC上时,连接CE,设AC,DE相交于点F,则图中的相似三角形(不含全等)有( )
A.1对 B.2对 C.3对 D.4对
14.如图所示,AB=3AC,BD=3AE,BD∥AC,点B,A,E在同一条直线上.求证:△ABD∽△CAE.
15.如图所示,在四边形ABCD中,∠B=∠ACD,AB=6,BC=4,AC=5,CD=,求AD的长.
16.如图所示,已知矩形ABCD的两条对角线相交于点O,过点A作AG⊥BD分别交BD、BC于点G、E.
(1)求证:BE2=EG·EA;
(2)连接CG,若BE=CE,求证:∠ECG=∠EAC.
17.如图所示,已知△ABC是等边三角形,点D、E分别在BC、AC上,且CD=CE,连接DE并延长至点F,使EF=AE,连接AF,CF,连接BE并延长,交CF于点G.
(1)求证:BC=DF;
(2)若BD=2DC,求证GF=2EG.
知识点四 相似三角形的判定定理3
18.若三角形甲的三边长分别为3,4,5,三角形乙的三边长分别为8,6,10,那么三角形甲和三角形乙( )
A.不一定相似 B.相似 C.一定不相似 D.无法确定是否相似
19.坐标平面上横、纵坐标都为整数的点叫做整点.已知点A(2,0),点B(3,1),O为坐标原点,在第一象限内取一整点C,使O,B,C三点所构成的三角形与△AOB相似,那么C点不同的位置一共有( )
A.1处 B.2处 C.3处 D.4处
20.△ABC的三边长分别为3,,,△A1B1C1的两边长分别为1和5,当△A1B1C1的第三边长为_________时,△ABC∽△A1B1C1.
21.如图所示,在正方形网格上有6个斜三角形:①△ABC,②△CDB,③△DEB,④△FBG,⑤HGF,⑥△EKF.请你写出与△ABC相似的三角形(写序号即可),并进行简要的证明.
巩固提高全练
22.如图所示,以A,B,C为顶点的三角形与以D,E,F为顶点的三角形相似,则这两个三角形的相似比为( )
A.2:1 B.3:1 C.4:3 D.3:2
23.如图所示,在△ABC中,点D、E分别在边AB、AC上,则在下列五个条件中:①∠AED=∠B;②DE∥BC;③;④AD·BC=DE·AC;⑤∠ADE=∠C,能满足△ADE∽△ACB的条件有( )
A.1个 B.2个 C.3个 D.4个
24.如图所示,已知AB∥CD,AD、BC相交于点E,AF分别交BC、CD于点F、G,∠FAE=∠ABE,则图中相似三角形的对数为( )
A.3 B.4 C.5 D.6
25.如图所示,点D是△ABC中AB边上的一点,且AD=2BD,连接CD,取点CD的中点E,连接B并延长,交AC于点F.若AC=5,则CF=___________.
26.在△ABC中,∠C=90°,AC=4,BC=3,D是边AB上的一点,AD=1,E是边AC上的一点(E与端点不重合),如果以A、D、E为顶点的三角形与△ABC相似,那么AE的长为___________.
27.如图所示,BD,CE是△ABC的高.求证:BA·AE=AC·AD.
28.如图所示,在△ABC中,DE∥BC,AD=5,BD=10,AE=3.
(1)求CE的长;
(2)在△ABC中,点Q在BC边上,且AQ交DE于点P.小明认为,你认为小明的结论正确吗?请说明你的理由.
29.如图所示,在等边△ABC中,P为BC上一点,D为AC上一点,且∠APD=60°,BP=3,CD=2.
(1)求证:△ABP∽△PCD;
(2)求△ABC的边长.
30.已知矩形ABCD中,点E是AD上一点,将矩形沿BE折叠,点A恰好落在BD上的点F处.
(1)如图①,若AB=3,AD=4,求AE的长;
(2)如图②,若点F恰好是BD的中点,点M是BD上一点,过点M做MN∥BE交AD于点N,连接EM,若MN平分∠EMD,求证:DN·DE=DM·BM.
31.在正方形网格中,每个小正方形的顶点称为格点,以格点为顶点的三角形叫做格点三角形.如图所示,△ABC是格点三角形,在图中的6×6正方形网格中作出格点三角形ADE(不含△ABC),使得△ADE∽△ABC(同一位置的格点三角形ADE只算一个),这样的格点三角形一共有( )
A.4个 B.5个 C.6个 D.7个
32.如图所示,在正方形ABCD中,点P是AB上一动点(不与A、B重合)对角线AC、BD相交于点O,过点P分别作AC、BD的垂线,分别交AC、BD于点E、F,交AD、BC于点M、N,下列结论:①△APE≌△AME;②PM+PN=AC;③PE2+PF2=PO2;④△POF∽△BNF;⑤点O在M、N两点的连线上.其中正确的是( )
A.①②③④ B.①②③⑤ C.①②③④⑤ D.③④⑤
33.如图所示,点C在∠AOB的内部,∠OCA=∠OCB,∠OCA与∠AOB互补.若AC=1.5,BC=2,则OC=__________.
34.如图所示,在△ABC中,D、E为边AB的三等分点,EF∥DG∥AC,H为AF与DG的交点.若AC=6,则DH=__________.
35.如图所示,在△ABC和△A´B´C´中,D、D´分别是AB、A´B´上一点,.
(1)当时,求证△ABC∽△A´B´C´;
证明的途径可以用如图所示的框图表示,请填写其中的空格:
(2)当时,判断△ABC与△A´B´C´是否相似,并说明理由.
36.如图所示,矩形ABCD中,AB=4,AD=6,点E为AD的中点,点P为线段AB上一个动点,连接EP,将△APE沿PE折叠得到△FPE,连接CE,CF,当△ECF为直角三角形时,AP的长为__________.
37.若一个三角形一条边的平方等于另两条边的乘积,我们把这个三角形叫做比例三角形.
(1)已知△ABC是比例三角形,AB=2,BC=3,请直接写出所有满足条件的AC的长;
(2)如图①,在四边形ABCD中,AD∥BC,对角线BD平分∠ABC,∠BAC=∠ADC求证:△ABC是比例三角形;
(3)如图②,在(2)的条件下,当∠ADC=90°时,求的值.
参考答案
1.B 2.C 3.C 4.C 5.B 6.A 7.△CBD
8.证明 ∵AB=AC,∠B=36°,∴∠C=36°.
又∵AC=DC,∴∠DAC=(180°-36°)÷2=72°.
∴∠DAB=180°-2×36°-72°=36°,∴∠DAB=∠C.
又∵∠B是公共角,∴△ABC∽△DBA.
9.证明 (1)∵BE=EC,∴∠EBC=∠C.
∵AG⊥BD,BG=GD,∴AB=AD,∴∠ABD=∠ADB.
∵∠ABD=∠ABE+∠EBC,∠ADB=∠DAC+∠C,∴∠ABE=∠DAC,即∠ABE=∠EAF.
(2)∵∠AEF=∠BEA,∠EAF=∠ABE,∴△AEF∽△BEA.
∴,∴AE2=EF·BE.
∵BE=EC,∴AE2=EF·EC.
10.C 11.D 12.A 13.C
14.证明 ∵BD∥AC,点B,A,E在同一条直线上,∴∠DBA=∠CAE.
又∵AB=3AC,BD=3AE,∴,∴△ABD∽△CAE.
15.解析 ∵AB=6,BC=4,AC=5,CD=,∴.
又∵∠B=∠ACD,∴△ABC∽△DCA.
∴,即,∴.
16.证明 (1)∵四边形ABCD是矩形,∴∠ABC=90.
∵AE⊥BD,∴∠BGE=90°.又∵∠AEB=∠BEG,∴△ABE∽△BGE.
∴,∴BE2=EG·EA.
(2)由(1)知BE2=EG·EA,
∵BE=CE,∴CE2=EG·EA,∴.
又∵∠CEG=∠AEC,∴△CEG∽△AEC,∴∠ECG=∠EAC.
17.证明 (1)∵△ABC是等边三角形,∴AB=AC=BC,∠ABC=∠ACB=60°,
又∵CD=CE,∴△CDE是等边三角形,∴∠CDE=∠ABC=60°,∴DF∥AB,
∵EF=AE,DE=CE,∴,
又∵∠AEF=∠CED,∴△AEF∽△CED,∴∠EAF=∠ECD,∴AF∥BC,
∴四边形ABDF是平行四边形,∴AB=DF,
又∵AB=BC,∴BC=DF.
(2)∵△CDE是等边三角形,
∴∠CDE=∠DCE=60°,CE=CD=DE.
在△BCE和△FDC中,∴△BCE≌△FDC,∴∠CBE=∠DFC,
又∵∠BED=∠FEG, ∴△BDE∽△FGE,,∴,
又∵CD=DE,BD=2DC,∴,∴GF=2EG.
18.B 19.C 20.
21.解析 ①△ABC的三边长之比是AB:AC:BC=1::.
③△DEB中,DE:BD:BE=2:2:=1::.
④△FBG中,FB:FG:BG=::5=1::.
⑤△HGF中,HG:HF:FG=:2:=1::.
其他两个三角形的三边长之比不符合,
故与△ABC相似的三角形的序号是③④⑤.
22.A 23.C 24.D 25. 26.或
27.证明 ∵BD,CE是△ABC的高,∴∠ADB=∠AEC=90°,
又∵∠A=∠A,∴△ADB∽△AEC,∴,
∴AD·AC=AE·AB,即BA·AE=AC·AD.
28.解析 (1)∵DE∥BC,∴∠ADE=∠ABC,∠AED=∠ACB,∴△ADE∽△ABC.
∴.
∵AD=5,BD=10,AE=3,∴CE=6.
(2)结论正确理由如下:
在△ABQ中,∵DP∥BQ,∴∠ADP=∠ABQ,∠APD=∠AQB,∴△ADP∽△ABQ,
∴.同理可得,∴.
29.解析 (1)证明:∵△ABC是等边三角形,∴AB=BC=AC,∠B=∠C=60°,
∴∠BAP+∠APB=180°-60°=120°.
∵∠APD=60°,∴∠APB+∠DPC=180°-60°=120°,∴∠BAP=∠DPC.
∵∠B=∠C,∠BAP=∠CPD,∴△ABP∽△PCD.
(2)∵△ABP∽△PCD,∴.
∵BP=3,CD=2,∴,解得AB=9,∴△ABC的边长为9.
30.解析(1)由折叠可知△ABE≌△FBE,∴∠A=∠EFB,BF=AB,AE=EF,
∵四边形ABCD为矩形,∴∠A=90°,∴∠EFD=90°,
在Rt△ABD中,BD==5,∴DF=BD-BF=5-3=2.
∵∠ADB=∠FDE,∠A=∠EFD=90°,∴△DEF∽△DBA,
∴,即,∴EF=,又∵AE=EF,∴AE=.
(2)证明:由(1)知∠EFD=90°,∴EF⊥BD,
又∵F是BD中点,∴直线EF为线段BD的垂直平分线,
∴BE=ED,∴∠EBD=∠EDB,∵MN∥BE,∴∠BEM=∠EMN,
又∵M平分∠EMD,∴∠EMN=∠NMD,∴∠BEM=∠NMD,∴△BEM∽△DMN,
∴,又∵BE=ED,∴,∴DN·DE=DM·BM.
31.A 32.B 33. 34.1
35.解析 (1);∠A=∠A´.
(2)相似.理由如下:如图,过点D、D´分别作DE∥BC、D'E'∥B'C',DE交AC于点E,D´E´交A´C´于点E´.
∵DE∥BC,∴△ADE∽△ABC,∴.同理,.
又,∴,∴.
同理,,∴,即,∴.
又,∴,
∴△DCE∽△D´C´E´,∴∠CED=∠C´E´D´.
∵DE∥BC,∴∠CED+∠ACB=180°,同理,∠C´E´D´+∠A´C´B´=180°.
∴∠ACB=∠A´C´B´.
又 ,∴△ABC∽△A´B´C´.
36.或1
37.解析 (1)△ABC是比例三角形,且AB=2,BC=3,
①当AB2=BC·AC时,得4=3AC,解得AC=;
②当BC2=AB·AC时,得9=2AC,解得AC=;
③当AC2=AB·BC时,得AC2=6,解得AC=(负值舍去).
经检验,AC=或AC=或AC=√6时,均符合题意
所以当AC=或或时,△ABC是比例三角形.
(2)证明∵AD∥BC,∴∠ACB=∠CAD,
又∵∠BAC=∠ADC,∴△ABC∽△DCA,∴,即CA2=BC·AD,
∵AD∥BC,∴∠ADB=∠CBD.
∵BD平分∠ABC,∴∠ABD=∠CBD,∴∠ADB=∠ABD,∴AB=AD,∴CA2=BC·AB,
∴△ABC是比例三角形.
(3)如图,过点A作AH⊥BD于点H,
∵AB=AD,∴BH=BD,∵AD∥BC,∠ADC=90°,∴∠BCD=90°,
∴∠BHA=∠BCD=90°,又∵∠ABH=∠DBC,∴△AB∽△DBC,
∴,即AB·BC=BH·DB,∴AB·BC=BD2,
又∵AB·BC=AC2,BD2=AC2,∴(负值舍去).










