2022年浙江省温州市中考数学备考模拟试卷（4份打包，含PDF校对版）

这是一份2022年浙江省温州市中考数学备考模拟试卷（4份打包，含PDF校对版），文件包含2022年浙江省温州市中考数学备考模拟试卷3doc、2022年浙江省温州市中考数学备考模拟试卷4doc、2022年浙江省温州市中考数学备考模拟试卷3pdf、2022年浙江省温州市中考数学备考模拟试卷1doc、2022年浙江省温州市中考数学备考模拟试卷2doc、2022年浙江省温州市中考数学备考模拟试卷1pdf、2022年浙江省温州市中考数学备考模拟试卷2pdf、2022年浙江省温州市中考数学备考模拟试卷4pdf等8份试卷配套教学资源，其中试卷共51页， 欢迎下载使用。

、选择题（本大题共10小题，每小题4分，共40分。在每小题给出的四个选项中，只有一个选项是符合题目要求的）
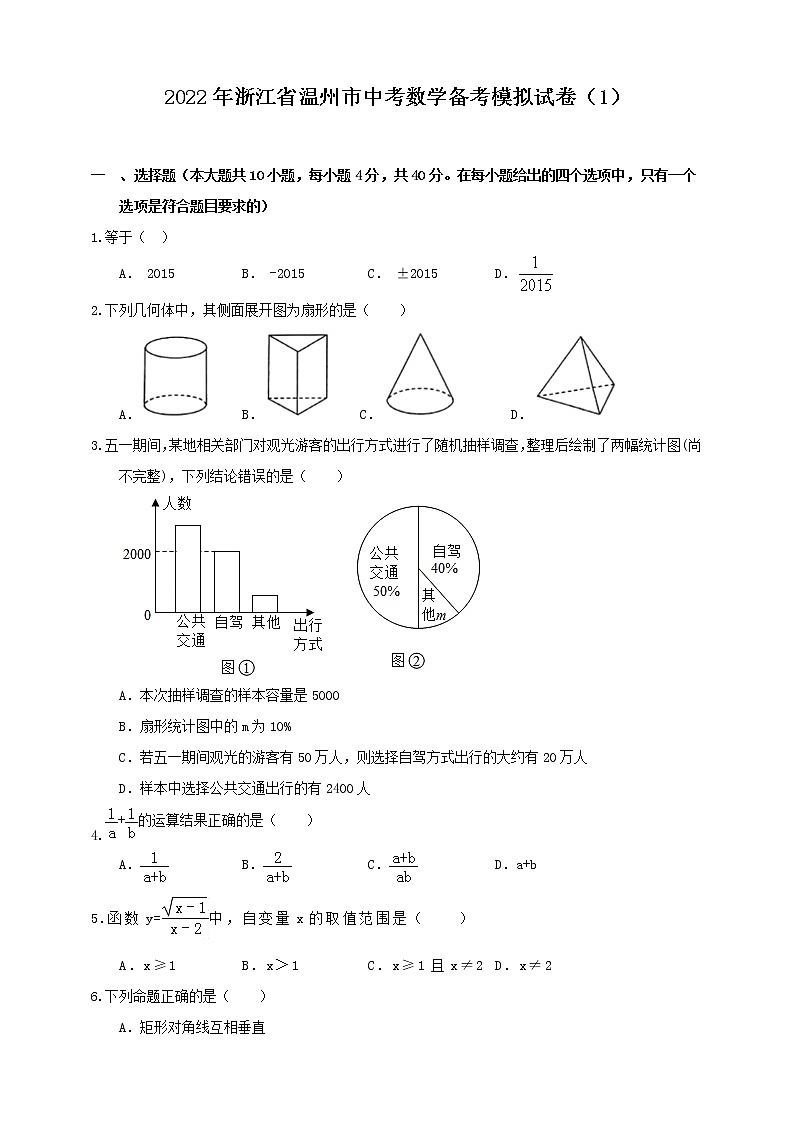
在成都举行的世界机场城市大会上，成都新机场规划蓝图首次亮相。新机场建成后，成都将成为继北京、上海之后，国内第三个拥有双机场的城市，按照远期规划，新机场将新建的4个航站楼的总面积约为万平方米，用科学计数法表示万为（ ）
A．B．C．D．
把一块直尺与一块三角板如图放置，若∠1=45°，则∠2的度数为（ ）
A．115°B．120°C．145°D．135°
如图是甲、乙两名射击运动员某节训练课的5次射击成绩的折线统计图，下列判断正确的是（ ）
A．乙的最好成绩比甲高B．乙的成绩的平均数比甲小
C．乙的成绩的中位数比甲小D．乙的成绩比甲稳定
化简+的结果是（ ）
A．x+1B．x﹣1C．x2﹣1D．
函数的自变量x的取值范围是（ ）
A．x＜1B．x＞1C．x≤1D．x≥1
若方程组的解满足x+y=0，则k的值为（ ）
A．﹣1B．1C．0D．不能确定
如图，工人师傅用角尺画出工件边缘AB的垂线a和b，得到a∥b，理由是（ ）
A．连结直线外一点与直线上各点的所有线段中，垂线段最短
B．在同一平面内，垂直于同一条直线的两条直线互相平行
C．在同一平面内，过一点有一条而且仅有一条直线垂直于已知直线
D．经过直线外一点，有且只有一条直线与这条直线平行
点A（﹣2，5）在反比例函数y=（k≠0）的图象上，则k的值是（ ）
A．10B．5C．﹣5D．﹣10
下列运算正确的是（ ）
A．B．
C．D．
不等式组的整数解是（ ）
A．0B．﹣1C．﹣2D．1
、填空题（本大题共6小题，每小题5分，共30分）
分解因式：mn2+2mn+m=______．
如图，由边长为1的小正方形组成的网格中，点A，B，C都在格点上，以为直径的圆经过点C和点D，则________．
已知圆锥的底面半径为20，侧面积为400π，则这个圆锥的母线长为 ．
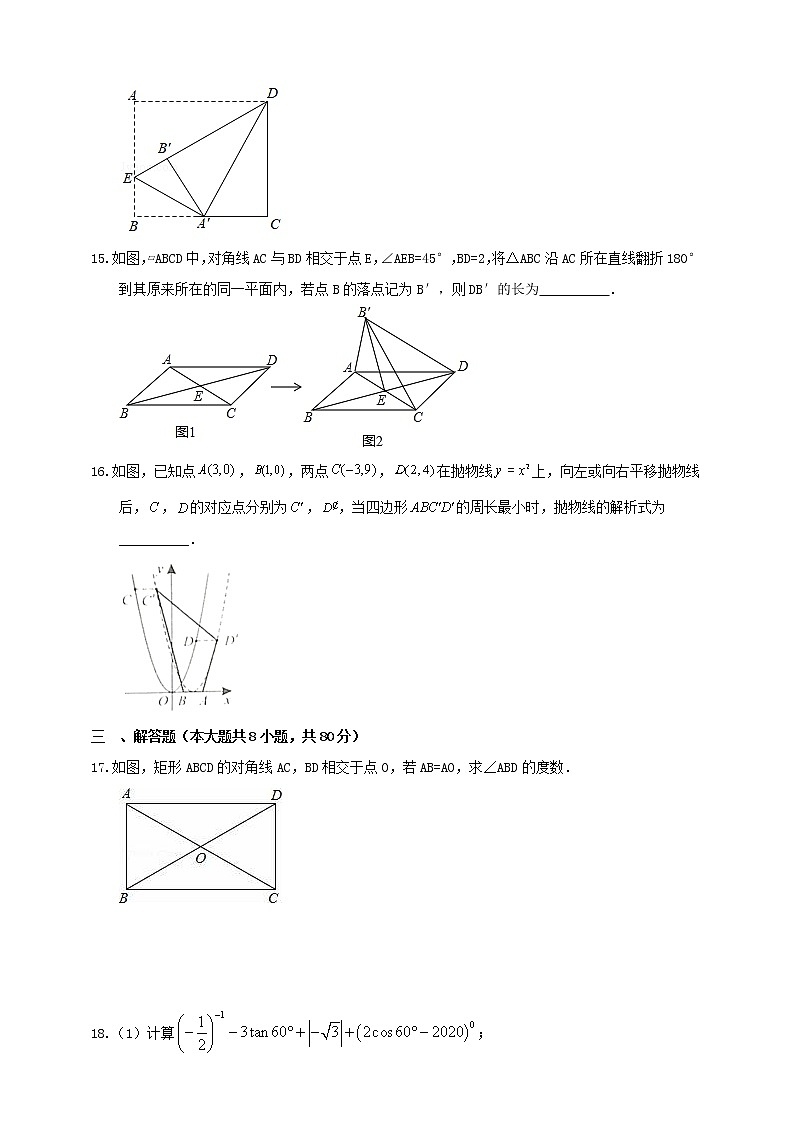
如图，在矩形ABCD中，AD＝2．将∠A向内翻折，点A落在BC上，记为A′，折痕为DE．若将∠B沿EA′向内翻折，点B恰好落在DE上，记为B′，则AB＝ ．
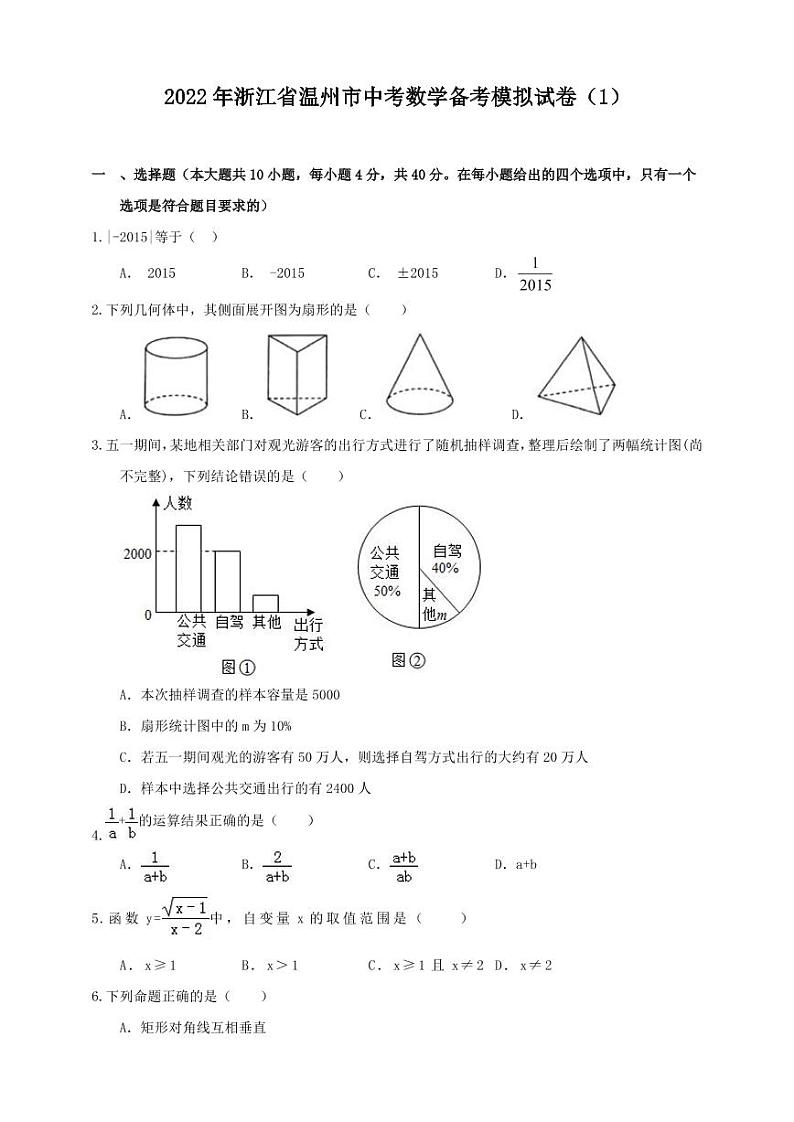
如图，▱ABCD中，对角线AC与BD相交于点E，∠AEB=45°，BD=2，将△ABC沿AC所在直线翻折180°到其原来所在的同一平面内，若点B的落点记为B′，则DB′的长为 ．
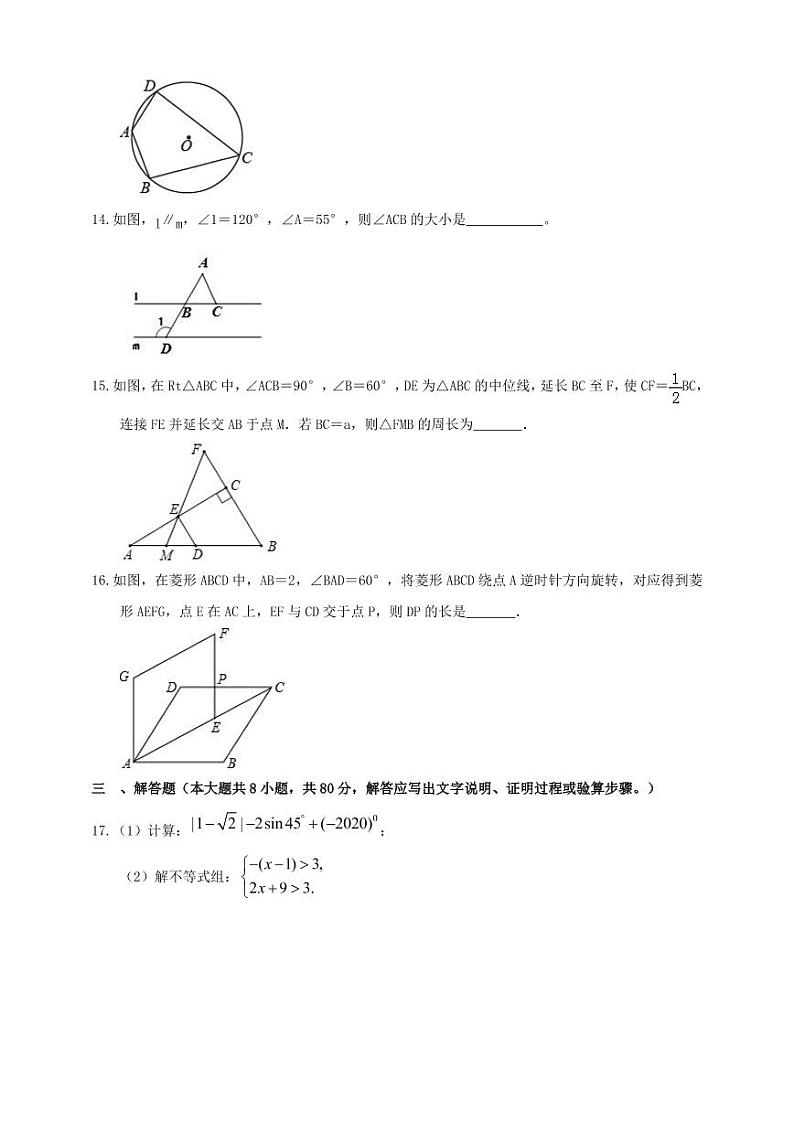
如图，已知点，，两点，在抛物线上，向左或向右平移抛物线后，，的对应点分别为，，当四边形的周长最小时，抛物线的解析式为__________．
、解答题（本大题共8小题，共80分）
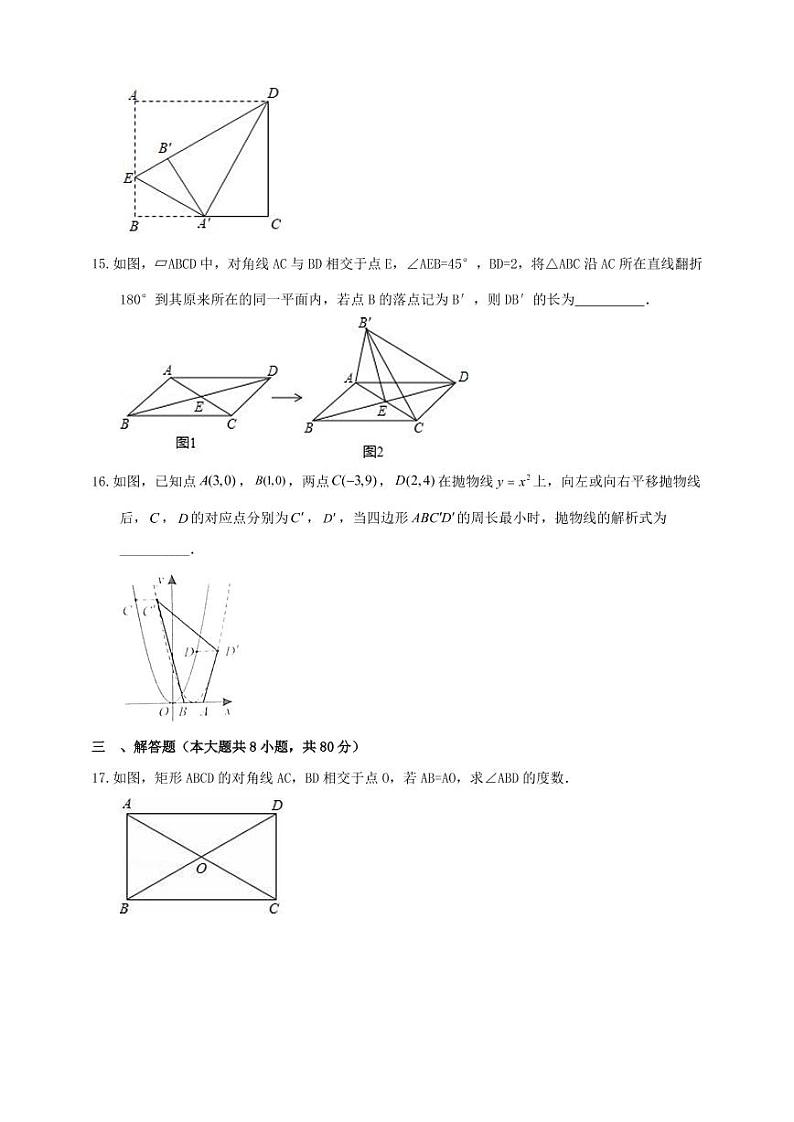
如图，矩形ABCD的对角线AC，BD相交于点O，若AB=AO，求∠ABD的度数．

（1）计算；
（2）解不等式组：．
如图是由边长为1的小正方形构成的的网格，点A，B均在格点上．

（1）在图1中画出以为边且周长为无理数的，且点C和点D均在格点上（画出一个即可）．
（2）在图2中画出以为对角线的正方形，且点E和点F均在格点上．
某校有学生3000人，现欲开展学校社团活动，准备组建摄影社、国学社、篮球社、科技制作社四个社团．每名学生最多只能报一个社团，也可以不报．为了估计各社团人数，现在学校随机抽取了50名学生做问卷调查，得到了如图所示的两个不完全统计图．
结合以上信息，回答下列问题：
（1）本次抽样调查的样本容量是 ，
（2）请你补全条形统计图，并在图上标明具体数据，
（3）求参与科技制作社团所在扇形的圆心角度数，
（4）请你估计全校有多少学生报名参加篮球社团活动．
某品牌汽车销售店销售某种品牌的汽车，每辆汽车的进价16（万元）．当每辆售价为22（万元）时，每月可销售4辆汽车．根据市场行情，现在决定进行降价销售．通过市场调查得到了每辆降价的费用（万元）与月销售量（辆）（）满足某种函数关系的五组对应数据如下表：
(1)请你根据所给材料和初中所学的函数知识写出与的关系式________；
(2)每辆原售价为22万元，不考虑其它成本，降价后每月销售利润y=(每辆原售价--进价)x，请你根据上述条件，求出月销售量为多少时，销售利润最大？最大利润是多少？
实验学校某班开展数学“综合与实践”测量活动．有两座垂直于水平地面且高度不一的圆柱，两座圆柱后面有一斜坡，且圆柱底部到坡脚水平线的距离皆为．王诗嬑观测到高度矮圆柱的影子落在地面上，其长为；而高圆柱的部分影子落在坡上，如图所示．已知落在地面上的影子皆与坡脚水平线互相垂直，并视太阳光为平行光，测得斜坡坡度，在不计圆柱厚度与影子宽度的情况下，请解答下列问题：
（1）若王诗嬑的身高为，且此刻她的影子完全落在地面上，则影子长为多少？
（2）猜想：此刻高圆柱和它的影子与斜坡的某个横截面一定同在一个垂直于地面的平面内．请直接回答这个猜想是否正确？
（3）若同一时间量得高圆柱落在坡面上的影子长为，则高圆柱的高度为多少？

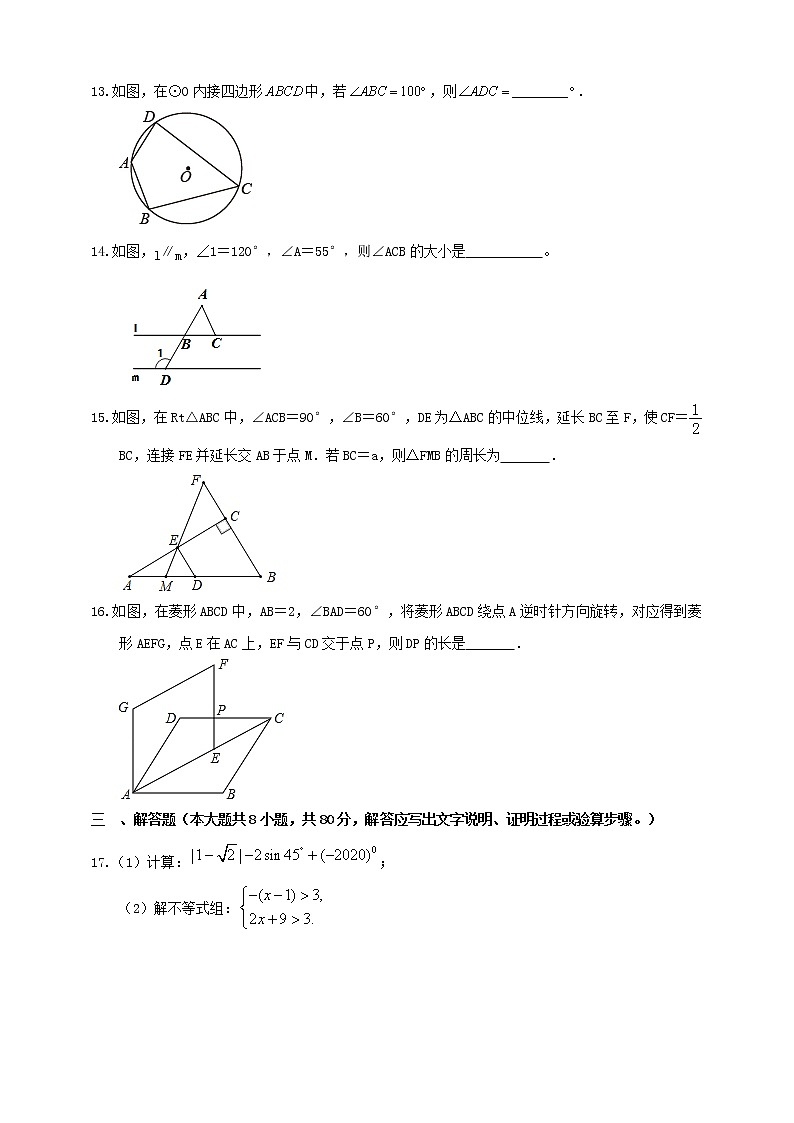
已知如图，以Rt△ABC的AC边为直径作⊙O交斜边AB于点E，连接EO并延长交BC的延长线于点D，点F为BC的中点，连接EF
（1）求证：EF是⊙O的切线；
（2）若⊙O的半径为3，∠EAC＝60°，求AD的长。
如图1，已知在平面直角坐标系xOy中，四边形OABC是矩形，点A，C分别在x轴和y轴的正半轴上，连结AC，OA＝3，tan∠OAC＝，D是BC的中点．
（1）求OC的长和点D的坐标，
（2）如图2，M是线段OC上的点，OM＝OC，点P是线段OM上的一个动点，经过P，D，B三点的抛物线交x轴的正半轴于点E，连结DE交AB于点F．
①将△DBF沿DE所在的直线翻折，若点B恰好落在AC上，求此时BF的长和点E的坐标，
②以线段DF为边，在DF所在直线的右上方作等边△DFG，当动点P从点O运动到点M时，点G也随之运动，请直接写出点G运动路径的长．
4
5
6
7
8
0
0.5
1
1.5
2