- 专题2.15 《一元一次不等式和一元一次不等式组》重难点突破(专项练习)-2021-2022学年八年级数学下册基础知识专项讲练(北师大版) 试卷 0 次下载
- 专题3.1 图形的平移(知识讲解)-2021-2022学年八年级数学下册基础知识专项讲练(北师大版)学案 学案 1 次下载
- 专题3.3 图形的旋转(知识讲解)-2021-2022学年八年级数学下册基础知识专项讲练(北师大版)学案 学案 0 次下载
- 专题3.4 图形的旋转(专项练习)-2021-2022学年八年级数学下册基础知识专项讲练(北师大版) 试卷 0 次下载
- 专题3.5 中心对称(知识讲解)-2021-2022学年八年级数学下册基础知识专项讲练(北师大版)学案 学案 0 次下载
专题3.2 图形的平移(专项练习)-2021-2022学年八年级数学下册基础知识专项讲练(北师大版)
展开专题3.2 图形的平移(专项练习)
一、单选题
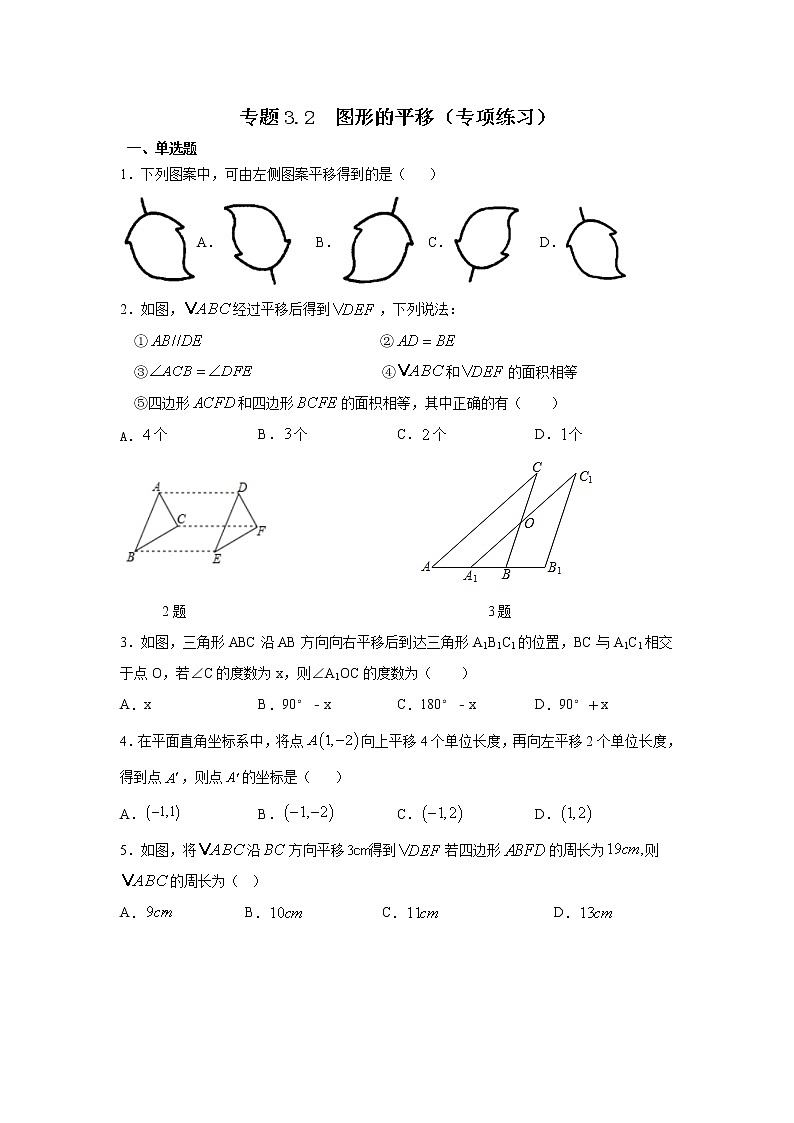
1.下列图案中,可由左侧图案平移得到的是( )
A. B. C. D.
2.如图,经过平移后得到,下列说法:
① ②
③ ④和的面积相等
⑤四边形和四边形的面枳相等,其中正确的有( )
A. 个 B.个 C.个 D.个
2题 3题
3.如图,三角形ABC沿AB方向向右平移后到达三角形A1B1C1的位置,BC与A1C1相交于点O,若∠C的度数为x,则∠A1OC的度数为( )
A.x B.90°﹣x C.180°﹣x D.90°+x
4.在平面直角坐标系中,将点向上平移4个单位长度,再向左平移2个单位长度,得到点,则点的坐标是( )
A. B. C. D.
5.如图,将沿方向平移得到若四边形的周长为则的周长为( )
A. B. C. D.
5题 6题
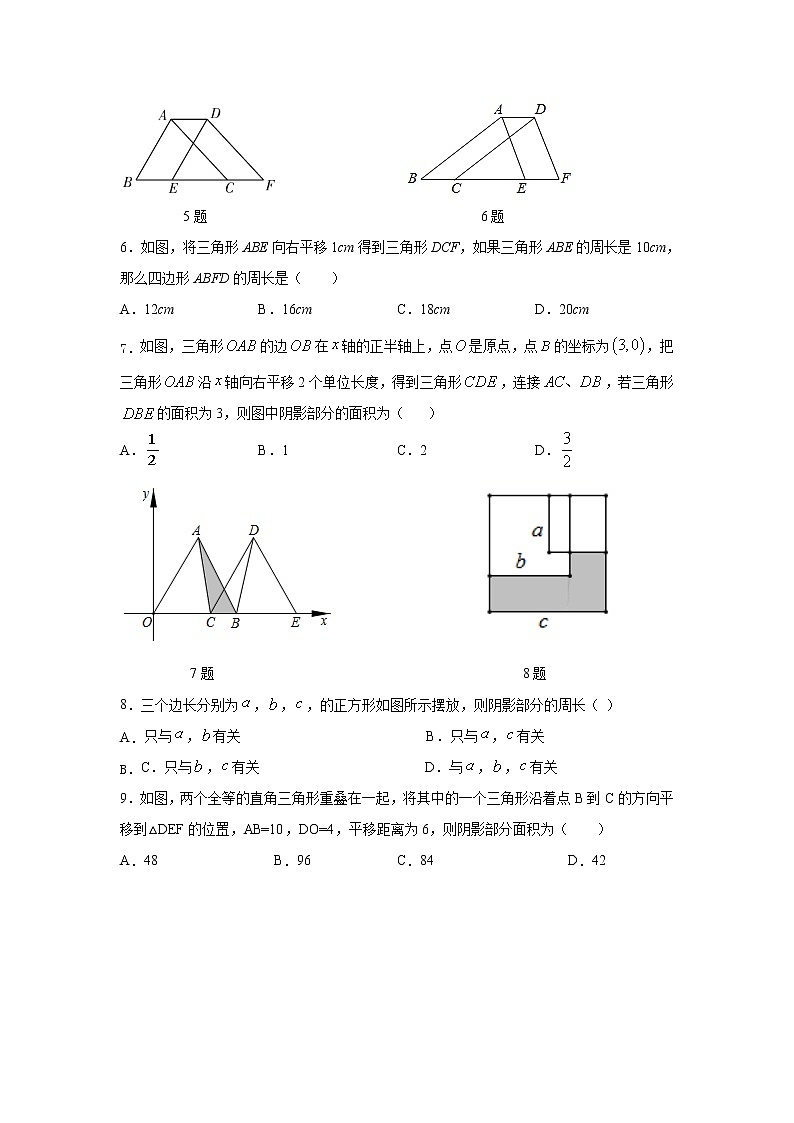
6.如图,将三角形ABE向右平移1cm得到三角形DCF,如果三角形ABE的周长是10cm,那么四边形ABFD的周长是( )
A.12cm B.16cm C.18cm D.20cm
7. 如图,三角形的边在轴的正半轴上,点是原点,点的坐标为,把三角形沿轴向右平移2个单位长度,得到三角形,连接,若三角形的面积为3,则图中阴影部分的面积为( )
A. B.1 C.2 D.
7题 8题
8.三个边长分别为,,,的正方形如图所示摆放,则阴影部分的周长( )
A. 只与,有关 B.只与,有关
B. C.只与,有关 D.与,,有关
9.如图,两个全等的直角三角形重叠在一起,将其中的一个三角形沿着点B到C的方向平移到△DEF的位置,AB=10,DO=4,平移距离为6,则阴影部分面积为( )
A.48 B.96 C.84 D.42
9题 10题
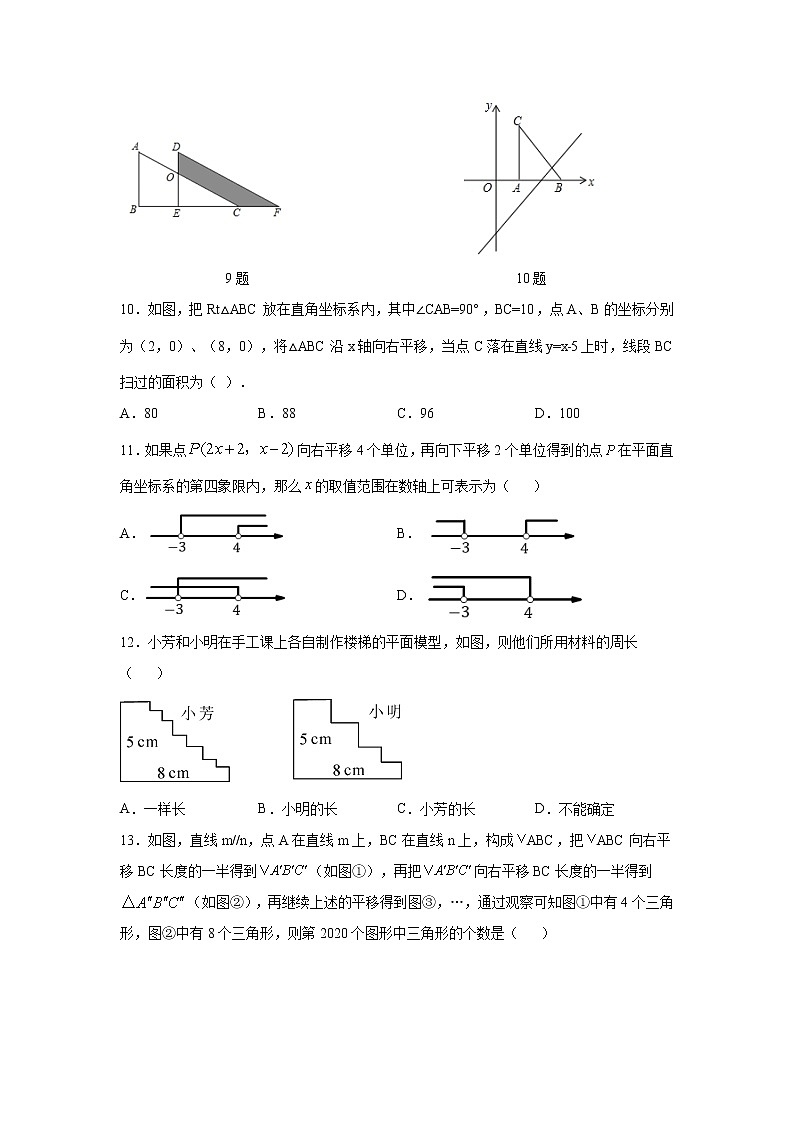
10.如图,把Rt△ABC放在直角坐标系内,其中∠CAB=90°,BC=10,点A、B的坐标分别为(2,0)、(8,0),将△ABC沿x轴向右平移,当点C落在直线y=x﹣5上时,线段BC扫过的面积为( ).
A.80 B.88 C.96 D.100
11.如果点向右平移4个单位,再向下平移2个单位得到的点在平面直角坐标系的第四象限内,那么的取值范围在数轴上可表示为( )
A. B.
C. D.
12.小芳和小明在手工课上各自制作楼梯的平面模型,如图,则他们所用材料的周长( )
A.一样长 B.小明的长 C.小芳的长 D.不能确定
13.如图,直线m//n,点A在直线m上,BC在直线n上,构成ABC,把ABC向右平移BC长度的一半得到(如图①),再把向右平移BC长度的一半得到(如图②),再继续上述的平移得到图③,…,通过观察可知图①中有4个三角形,图②中有8个三角形,则第2020个图形中三角形的个数是( )
A.4040 B.6060 C.6061 D.8080
14.如图,在平面直角坐标系中,点在轴上,点的坐标为.将先绕点顺时针旋转90°,再向右平移3个单位长度,则变换后点的对应点坐标是( )
A. B. C.(3,2) D.(2,2)
二、填空题
15.如图,直线y=kx+1经过点A(-2,0)交y轴于点B,以线段AB为一边,向上作等腰RtABC,将ABC向右平移,当点C落在直线y=kx+1上的点F处时,则平移的距离是_________.
16.如图,在△ABC中,AB=4,BC=6,∠B=60°,将△ABC沿射线BC的方向平移2个单位后,得到,连接,则的周长为________.
17.如图,在长方形草地内修建了宽为2米的道路,则草地面积为_______米2.
18.如图,把直角梯形沿方向平移到梯形,,,,则阴影部分的面积是___
19.如图,在平面直角坐标系中,点A在第一象限,点B在y轴上,点C坐标为(-1,0).OAB是以OB为斜边的等腰直角三角形,OB=4.若将OAB向左平移,使点A落在直线BC上,则平移的距离是__________.
20.如图,将直角三角形ABC沿斜边AC的方向平移到三角形DEF的位置,DE交BC于点G,BG=4,EF=12,△BEG的面积为4,下列结论:①DE⊥BC;②△ABC平移的距离是4;③AD=CF;④四边形GCFE的面积为20,其中正确的结论有________(只填写序号).
21.在平面直角坐标系中,将直线的图象向上平移3个单位,所得到直线与坐标轴围成的三角形面积为__________.
22.在下图中,将图1中的,沿翻折得到图2,将图2中的不动,把向左平移得图3,则图3中有__________个等腰三角形.
23.如图,在平面直角坐标系中,已知、、,平移线段至线段,点在四边形内,满足,,则点的坐标为________.
24.如图,在平面直角坐标系xOy中,对正方形ABCD及其内部的每个点进行如下操作:把每个点的横、纵坐标都乘以同一种实数a,将得到的点先向右平移m个单位,再向上平移n个单位(m0,n0),得到正方形A′B′C′D′及其内部的点,其中点A,B的对应点分别为A′,B′,则a=_____,m=_____,n=_____.若正方形ABCD内部的一个点F经过上述操作后得到的对应点F′与点F重合,则点F的坐标为_____.
25.如图,△ABC中,∠C=90°,AC=5cm,CB=12cm,AB=13cm,将△ABC沿直线CB向右平移3cm得到△DEF,DF交AB于点G,则点C到直线DE的距离为______cm.
三、解答题
26.如图,在四边形ABCD中,AD∥BC,且AD<BC,AC、BD为两条对角线,且AC⊥BD,AC=BD,
(1)把AC平移到DE的位置,方向为射线AD的方向,平移的距离为线段AD的长;
(2)判断△BDE的形状.
27.如图,在平面直角坐标系中,已知点、和,,,将平移可得到,点,,的对应点分别为点,,.
(1)求点的坐标.(2)求直线与轴的交点坐标.
28.如图,在直角坐标系中,点分别在轴、轴正半轴上,,三角形的面积为10.点在第二象限,点是射线上一动点,.
(1)求点的坐标.
(2)线段能否通过平移得到?试求点的坐标.
(3),,之间有何关系?请说明理由.
参考答案
1.D
【分析】根据平移的性质可直接进行排除选项.
故选D.
2.A
【分析】根据平移的性质逐一判断即可.
解:经过平移后得到,
∴,故①正确;
,故②正确;
,故③正确;
和的面积相等,故④正确;
四边形和四边形都是平行四边形,且,即两个平行四边形的底相等,但高不一定相等,
∴四边形和四边形的面枳不一定相等,故⑤不正确;
综上:正确的有4个
故选A.
【点拨】此题考查的是图形的平移,掌握平移的性质是解题关键.
3.C
【分析】根据平移性质得出,∠C1=∠C,根据平行线性质得出∠COC1=∠C1,进而得出∠A1OC的度数.
解:∵三角形ABC沿AB方向向右平移后到达三角形A1B1C1的位置,BC与A1C1相交于点O,
∴∠C1=∠C,,
∴∠COC1=∠C1(两直线平行内错角相等),
∴∠A1OC=180°﹣x,
故选:C.
【点拨】本题考查了平移的性质,运用平行线的性质得出∠COC1=∠C1是解题关键.
4.C
【分析】根据“向左平移横坐标减,向上平移纵坐标加”求解即可.
解:将点向上平移4个单位长度,再向左平移2个单位长度,得到点,
点的横坐标为,纵坐标为,
的坐标为.
故选:C.
【点拨】本题考查了坐标与图形变化平移,平移中点的变化规律是:横坐标右移加,左移减;纵坐标上移加,下移减.
5.D
【分析】由平移的性质可得AD=CF=3cm,AC=DF,再由四边形ABFD的周长为19cm,可得
AB+BC+CF+DF+AD=19cm,由此即可求得AB+BC+AC=13cm.
【详解】∵将△ABC沿BC方向平移3cm得到△DEF,
∴AD=CF=3cm,AC=DF,
∵四边形ABFD的周长为AB+BC+CF+DF+AD=19cm,
∴AB+BC+AC=AB+BC+DF=19- AD-CF
即19-3-3= 13(cm),
即三角形ABC的周长为13cm.
故选D.
【点拨】本题主要考查平移的性质,熟练运用平移的性质是解决问题的关键.
6.A
【分析】先根据平移的性质得DF=AC,AD=CF==EF=1cm,再由△ABE的周长为10cm得到AB+BE+AE=10cm,然后利用等线段代换可计算出AB+BE+EF+DF+AD =12(cm),于是得到四边形ABFD的周长为12cm.
解:∵△ABE的周长=AB+BE+AE=10(cm),由平移的性质可知,BC=AD=EF=1(cm),AE=DF,
∴四边形ABFD的周长=AB+BE+EF+DF+AD=10+1+1=12(cm).
故答案为:A.
【点拨】本题考查了平移的性质:把一个图形整体沿某一直线方向移动,会得到一个新的图形,新图形与原图形的形状和大小完全相同;新图形中的每一点,都是由原图形中的某一点移动后得到的,这两个点是对应点.连接各组对应点的线段平行且相等.
7.D
【分析】根据平移的性质和等高的三角形面积比等于底边的比即可求解.
解:点的坐标为,把三角形沿轴向右平移2个单位长度,
,,
图中阴影部分与三角形等高,三角形的面积为3,
图中阴影部分的面积为.
故选:.
【点拨】本题考查了坐标与图形变化平移,三角形的面积,关键是得到三角形和图中阴影部分的底.
8.B
【分析】将阴影部分横向的边和纵向的边分别往一个方向平移即可求解.
解:阴影部分的周长:
故选:B.
【点拨】此题主要考查不规则阴影图形的周长,熟练掌握平移法是解题关键.
9.A
【分析】根据平移的性质得出BE=6,DE=AB=10,则OE=6,则
阴影部分面积=S四边形ODFC=S梯形ABEO,根据梯形的面积公式即可求解.
解:由平移的性质知,BE=6,DE=AB=10,
∴OE=DE-DO=10-4=6,
∴S四边形ODFC=S梯形ABEO= (AB+OE)•BE=(10+6)×6=48.
故选A.
【点拨】本题主要考查了平移的性质及梯形的面积公式,得出阴影部分和梯形ABEO的面积相等是解题的关键.
10.B
解:∵点A、B的坐标分别为(2,0)、(8,0),
∴AB=6,
∵∠CAB=90°,BC=10,
∴CA= =8,
∴C点纵坐标为:8,
∵将△ABC沿x轴向右平移,当点C落在直线y=x﹣5上时,
∴y=8时,8=x﹣5,解得:x=13,即A点向右平移13﹣2=11个单位,
∴线段BC扫过的面积为:11×8=88.
故选B.
11.C
【分析】直接利用平移中点的变化规律得出点平移后的坐标,再根据第四象限点的横坐标大于0,纵坐标小于0,列出关于x的不等式组,求出不等式组的解集,表示在数轴上即可得到结果.
解:点向右平移4个单位,再向下平移2个单位;
平移后点P的坐标为;
平移后点P在第四象限内;
解得:-3
故选:C.
【点拨】此题考查了平移中点的变化规律,在数轴上表示不等式组的解集,解一元一次不等式组,以及点的坐标,列出不等式组是本题的突破点.
12.A
【分析】首先根据已知图形中两个图形中共同含有的边,再判断形状不同的边的长度即可.
解:两个图形右侧边与左侧相等,上侧与下侧相等,
即两个图形都可以利用平移的方法变为长为8cm,宽为5cm的矩形,
所以两个图形的周长都为(8+5)×2=26(cm),
所以他们用的材料一样长.
故选:A.
【点拨】此题主要考查了平移的应用,考生通过观察、分析识别图形的能力,解决此题的关键是通过观察图形确定右侧与上侧各边的长相等.
13.D
【分析】探究规律,利用规律解决问题即可.
解:观察图可得,第1个图形中大三角形有2个,小三角形有2个,
第2个图形中大三角形有4个,小三角形有4个,
第3个图形中大三角形有6个,小三角形有6个,…
依次可得第n个图形中大三角形有2n个,小三角形有2n个.
故第2019个图形中三角形的个数是:2×2020+2×2020=8080.
故选:D.
【点拨】本题考查规律型问题,平行线的性质,平移变换等知识,解题的关键是学会探究规律的方法,属于中考常考题型.
14.D
【分析】先求出A点绕点顺时针旋转90°后所得到的的坐标,再求出向右平移3个单位长度后得到的坐标,即为变换后点的对应点坐标.
解:将先绕点顺时针旋转90°,得到点坐标为(-1,2),再向右平移3个单位长度,则点的纵坐标不变,横坐标加上3个单位长度,故变换后点的对应点坐标是(2,2).
【点拨】本题考察点的坐标的变换及平移.
15.5
【分析】先把A坐标代入y=kx+1求得k=,则直线AB的解析式为y=x+1,再确定B点坐标(0,1),作CH⊥x轴于H,如图,根据等腰直角三角形的性质得AC=AB,∠BAC=90°,接着证明△ABO≌△CAH,得到OB=AH=1,OA=CH=2,于是可确定C点坐标(-3,2),然后根据平移的性质得点F的纵坐标与C点的纵坐标相等,则可把y=2代入y=x+1得x+1=2,解得x=2,所以F点的坐标为(2,2),点F与点C的横坐标之差就是平移的距离.
解:把A(-2,0)代入y=kx+1
得-2k+1=0,解得k=,
则直线AB的解析式为y=x+1,
当x=0时,y=x=1=1,
则B点坐标为(0,1),
如图,作CH⊥x轴于H
∵△ABC为等腰直角三角形,
∴AC=AB,∠BAC=90°,
∴∠BAO+∠CAH=90°,而∠BAO+∠ABO=90°,
∴∠ABO=∠CAH,
在△ABO和△CAH中,,
∴△ABO≌△CAH,
∴OB=AH=1,OA=CH=2,
∴OH=OA+AH=3,
∴C点坐标为(-3,2),
∵△ABC向右平移,
∴F的纵坐标与C点的纵坐标相等,
把y=2代入y=x+1得x+1=2,
解得x=2,
∴F点的坐标为(2,2),
∴点C向右平移了2-(-3)=5个单位.
故答案为5.
【点拨】本题考查了一次函数图象上点的坐标特征:一次函数y=kx+b,(k≠0,且k,b为常数)的图象是一条直线.它与x轴的交点坐标是(-bk,0);与y轴的交点坐标是(0,b).直线上任意一点的坐标都满足函数关系式y=kx+b.也考查了等腰直角三角形的性质和平移的性质.
16.12
【分析】根据平移的性质得,,,则可计算,则,可判断为等边三角形,继而可求得的周长.
解:平移两个单位得到的,
,,
,,
,,
,
又,
,
是等边三角形,
的周长为.
故答案为:12.
【点拨】本题考查了平移的性质:把一个图形整体沿某一直线方向移动,会得到一个新的图形,新图形与原图形的形状和大小完全相同.新图形中的每一点,都是由原图形中的某一点移动后得到的,这两个点是对应点.连接各组对应点的线段平行且相等.
17.144
【分析】先求出道路的总长度,进而求出道路的面积,最后用总面积减去道路的面积即可.
解:由图形得到了的总长度为20+10-2=28米,
所以道路的总面积为28×2=56米2,
所以草地面积为20×10-56=144米2.
故答案为:144
【点拨】本题考查了请不规则图形的面积,根据题意求出道路的总长度是解题关键,注意应减去重合的部分.
18.130cm2.
【分析】根据平移的性质可知梯形EFGH≌梯形ABCD,那么GH=CD,BC=FG,观察可知梯形EFMD是两个梯形的公共部分,那么阴影部分的面积就等于梯形MGHD,再根据梯形的面积计算公式计算即可.
解:∵直角梯形EFGH是由直角梯形ABCD平移得到的,
∴梯形EFGH≌梯形ABCD,
∴GH=CD,BC=FG,
∵梯形EFMD是两个梯形的公共部分,
∴S梯形ABCD-S梯形EFMD=S梯形EFGH-S梯形EFMD,
∴S阴影=S梯形MGHD=(DM+GH)•GM=(28-4+28)×5=130(cm2).
故答案是130cm2.
【点拨】本题考查了图形的平移,解题的关键是知道平移前后的两个图形全等.
19.
【分析】分别求出A点坐标及直线BC解析式即可.
解:如图,过A作AD⊥OB于D,
∵OAB是以OB为斜边的等腰直角三角形,OB=4.
∴OD=AD=2
∴A(2,2)
∵B(0,4),C(-1,0).
∴直线BC解析式为
∴在直线BC上当时,
∴A平移的距离为
故答案为
【点拨】本题考查一次函数与平移,左右平移纵坐标不变是解题的关键.
20.①③④
【分析】根据平移的性质分别对各个小题进行判断:①利用平移前后对应线段是平行的即可得出结果;②平移距离指的是对应点之间的线段的长度;③根据平移前后对应线段相等即可得出结果;④利用梯形的面积公式即可得出结果.
解:∵直角三角形ABC沿斜边AC的方向平移到三角形DEF的位置,
∴AB∥DE,
∴∠ABC=∠DGC=90°,
∴DE⊥BC,
故①正确;
△ABC平移距离应该是BE的长度,BE>4,
故②错误;
由平移前后的图形是全等可知:AC=DF,
∴AC-DC=DF-DC,
∴AD=CF,
故③正确;
∵△BEG的面积是4,BG=4,
∴EG=4×2÷4=2,
∵由平移知:BC=EF=12,
∴CG=12-4=8,
四边形GCFE的面积:(12+8)×2÷2=20,
故④正确;
故答案为:①③④
【点拨】本题主要考查的是平移的性质,正确的掌握平移的性质是解题的关键.
21.4
【分析】向上平移3个单位得到,从而可以求与x、y轴交点的坐标,得到线段的长度,再利用三角形的面积公式即可求解
解:向上平移3个单位得到,
的图象如图所示:
令,得,
∴,
令,得,
∴,
∴,,
∴,
故答案为:4.
【点拨】本题主要考察一次函数的平移,熟记平移法则是解决本题的关键
22.3
【分析】先标出图三交点的字母,然后根据对称的性质便可求解.
解:图三标上字母如图所示
根据对称性,是等腰三角形的有:三个
故答案为:3.
【点拨】本题考查等腰三角形的判断,以及对称平移变换,属于基础题.
23.
【分析】根据题意画出图形,设,利用平移的性质及已知点的坐标可求出,,,的长,利用三角形的面积公式分别求出,,的面积,再根据,可求出与的关系式,从而可得到点的坐标,再根据,建立关于的方程组,解方程组求出的值,即可得到点的坐标.
解:如图,
设,
∵,,,
∵平移线段至线段,
∴,,,
∴,
∵
,
∵,∴
∴,∴点
∵,
∴
∵解之:
∴点
【点拨】本题主要考查了坐标与图形性质,平行线的性质,三角形的面积,坐标与图形变化-平移,根据题意画出图形是解题的关键.
24. 2 (1,4)
【分析】首先根据点A到A′,B到B′的点的坐标可得方程组,,解可得a、m、n的值,设F点的坐标为(x,y),点F′点F重合可列出方程组,再解可得F点坐标.
解:由点A到A′,可得方程组;
由B到B′,可得方程组,
解得,
设F点的坐标为(x,y),点F′点F重合得到方程组,
解得,
即F(1,4),
故答案为:,,2,(1,4).
【点拨】本题主要考查了坐标与图形变化-平移以及二元一次方程组的应用,关键是正确理解题意,根据点的坐标列出方程组.
25.
【分析】根据平移前后图形的大小和形状不变,添加辅助线构造梯形,利用面积相等来计算出答案.
解:如图,连接AD、CD,作CH⊥DE于H,
依题意可得AD=BE=3cm,
∵梯形ACED的面积,
∴,
解得;
故答案为:.
【点拨】
本题考查的是图形的平移和点到直线的距离,注意图形平移前后的形状和大小不变,以及平移前后对应点的连线相等.
26.(1)答案见解析;(2)等腰直角三角形
【分析】
(1)延长BC至E,使CE=AD,连接DE即可;
(2)根据平移的性质可得DE∥AC,DE=AC,再根据两直线平行,内错角相等求出∠BDE=90°,然后根据等腰直角三角形的定义判定即可.
解:(1)如图所示,DE即为所求;
(2)由平移的性质得,DE∥AC,DE=AC,
∵AC=BD,
∴BD=DE,
∴△BDE是等腰直角三角形.
【点拨】
本题考查了利用平移变换作图,等腰直角三角形的判定,熟练掌握平移的性质是解题的关键.
27.(1);(2).
【分析】
(1)过点作轴于点,过点作轴于点;先说明,再证可得,;由、可得、、,然后再求得CN和ON的长,最后结合点C所在的象限即可解答;
(2)先求出F点的坐标,进而求得直线EF的解析式,令x=0,求得函数值y即可.
解:(1)如图,过点作轴于点,过点作轴于点,则,
∴.
∵,∴,
∴.
在和中,
∴,
∴,.
∵,.
∴,,,
∴,,
∴点的坐标为;
(2)∵在平移过程中,点对应点,点对应点,
∴.
设直线的函数表达式为,
则,
解得
∴直线的函数表达式为.
令,则,
∴直线与轴的交点坐标为.
【点拨】本题主要考查了一次函数图象上点的坐标特征、三角形全等的判定和性质、待定系法求一次函数的解析式、平移变换等知识点,正确作出辅助线、求得点C的坐标成为解答本题的关键.
28.(1);(2)线段能通过平移得到,详见解析;;(3)或∠OPA=∠POC-∠PAB ,详见解析
【分析】
(1)由,可设,,根据三角形的面积公式,求得的值即可解题;
(2)根据题意点,的纵坐标相同,点O,A在横轴上,即可以通过平移得到,根据平移的性质解题;
(3)分两种情况讨论:一种是当点在点、点之间时, 另一种是当点在点右边时,分别作OC的平行线,根据平行线定理解题即可.
解:(1)如图 1,由,可设,
∵三角形的面积为10
∴
∴
∴正数
∴
∴
(2)线段能通过平移得到.
理由:如图 1,∵,的纵坐标相同
∴轴
∴
∵,
∴.
∴
∴线段能通过平移得到
由(1),
将向左平移5个单位,点到点,点到点.
∴
(3)如图 1,当点在点、点之间时,
.
理由:作.
∴.
∵,
∴.
∴.
∴.
即.
如图 2,当点在点右边时,
.
作.
∴.
∵,
∴.
∴.
∴.
【点拨】本题考查三角形面积公式、平移的性质、两直线平行内错角相等等知识,都是常见考点,难度较易,准确作出适当的辅助线有助于解题.
专题5.10 分式方程(专项练习)-2021-2022学年八年级数学下册基础知识专项讲练(北师大版): 这是一份专题5.10 分式方程(专项练习)-2021-2022学年八年级数学下册基础知识专项讲练(北师大版),共19页。试卷主要包含了单选题,填空题,解答题等内容,欢迎下载使用。
专题5.2 认识分式(专项练习)-2021-2022学年八年级数学下册基础知识专项讲练(北师大版): 这是一份专题5.2 认识分式(专项练习)-2021-2022学年八年级数学下册基础知识专项讲练(北师大版),共16页。试卷主要包含了单选题,填空题,解答题等内容,欢迎下载使用。
专题3.12 旋转-基础知识常考题(专项练习)-2021-2022学年八年级数学下册基础知识专项讲练(北师大版): 这是一份专题3.12 旋转-基础知识常考题(专项练习)-2021-2022学年八年级数学下册基础知识专项讲练(北师大版),共25页。试卷主要包含了单选题,填空题,解答题等内容,欢迎下载使用。












