

- 专题1.11 《三角形的证明》全章复习与巩固(专项练习)-2021-2022学年八年级数学下册基础知识专项讲练(北师大版) 试卷 0 次下载
- 专题1.12 《三角形的证明》专题练习(基础篇)-2021-2022学年八年级数学下册基础知识专项讲练(北师大版) 试卷 2 次下载
- 专题2.1 不等关系及不等式的基本性质(知识讲解)-2021-2022学年八年级数学下册基础知识专项讲练(北师大版)学案 学案 1 次下载
- 专题2.2 不等关系及不等式的基本性质(专项练习)-2021-2022学年八年级数学下册基础知识专项讲练(北师大版) 试卷 0 次下载
- 专题2.3 一元一次不等式的解法(知识讲解)-2021-2022学年八年级数学下册基础知识专项讲练(北师大版)学案 学案 0 次下载
专题1.13 《三角形的证明》专题练习(提升篇)-2021-2022学年八年级数学下册基础知识专项讲练(北师大版)
展开专题1.13 《三角形的证明》专题练习(提升篇)
一、单选题
1.如图,在中,,,AB的中点为D.以C为原点,射线CB为x轴的正方向,射线CA为y轴的正方向建立平面直角坐标系.P是BC上的一个动点,连接AP、DP,则最小时,点P的坐标为( )
A. B. C. D.
2.如图,C是线段AB上的一点,和都是等边三角形,AE交CD于M,BD交CE于N,交AE于,则①;②;③;④;⑤是等边三角形.其中,正确的有( )
A.2个 B.3个 C.4个 D.5个
3.如图,平分,于点,于点,延长,交, 于点,,下列结论错误的是( )
A. B.
C. D.
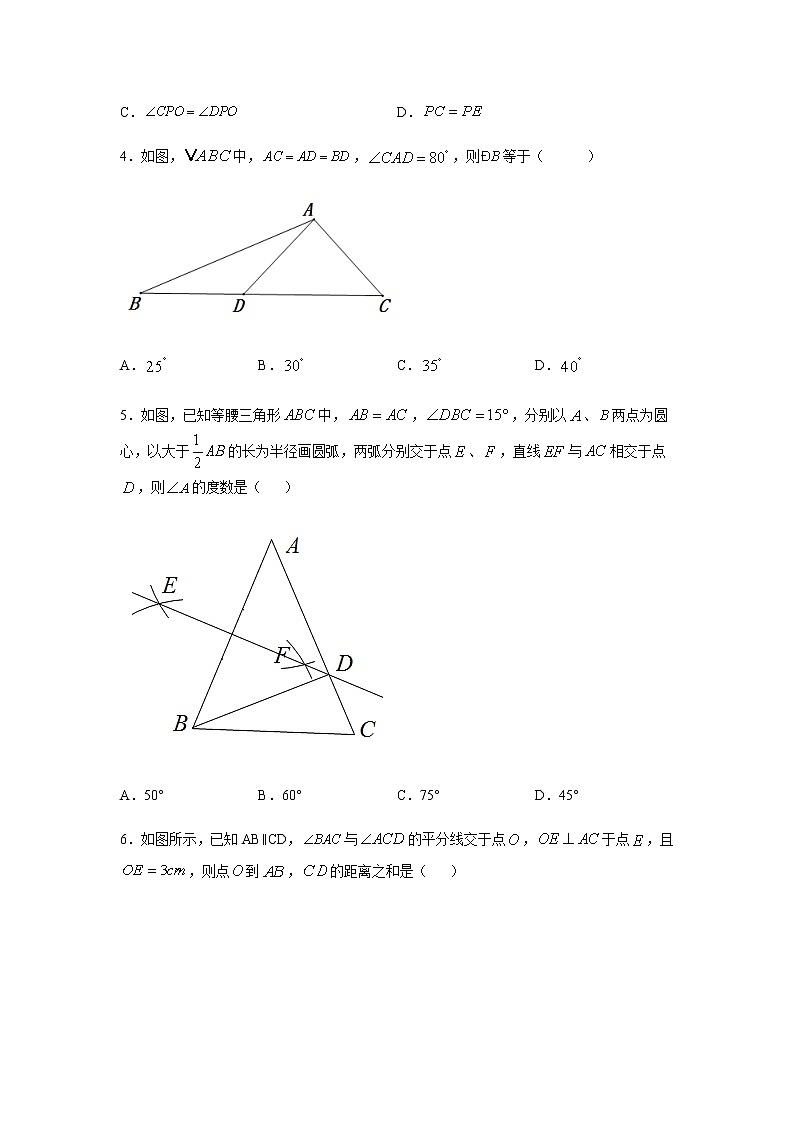
4.如图,中,,,则等于( )
A. B. C. D.
5.如图,已知等腰三角形中,,,分别以、两点为圆心,以大于的长为半径画圆弧,两弧分别交于点、,直线与相交于点,则的度数是( )
A.50° B.60° C.75° D.45°
6.如图所示,已知AB∥CD,与的平分线交于点,于点,且,则点到,的距离之和是( )
A. B. C. D.
7.如图,已知AD为的高线,,以AB为底边作等腰,连接ED,EC延长CE交AD于F点,下列结论:①;②;③;④为等腰三角形;⑤,其中正确的有( )
A.①③⑤ B.①②④ C.①③④ D.①②③⑤
8.如图,,点D在AC边上,AE和BD相交于点O,若,,则的度数为( )
A.45° B.40° C.35° D.30°
9.如图,在中,DE是AC的垂直平分线,交AC边于E,交BC边于D,连接AD,若,的周长为13,则的周长( )
A.16 B.19 C.20 D.24
10.如图,在中,,,点M从点A出发以每秒的速度向点C运动,点N从点C出发以每秒的速度向点B运动,其中一个动点到达终点时,另一个动点也随之停止运动,当是以为底的等腰三角形时,则这时等腰三角形的腰长是( )
A. B. C. D.
11.若是的边,且则是( ).
A.锐角三角形 B.直角三角形 C.钝角三角形 D.等边三角形
12.如图,在等边△ABC中,AB=2.N为AB上一点,且AN=1,∠BAC的平分线交BC于点D.M是AD上的动点,连结BM、MN.则BM+MN的最小值是( )
A. B.2 C.1 D.3
13.如图所示,已知点,一次函数的图象与两坐标轴分别交于A,B两点,M,P分别是线段OB,AB上的动点,则的最小值是( )
A.4 B.5 C. D.
14.如图,在中,点D是BC边上一点,已知,,CE平分交AB于点E,连接DE,则的度数为( )
A. B. C. D.
二、填空题
15.如图,C为∠AOB的边OA上一点,过点C作CD∥OB交∠AOB的平分线OE于点F,作CH⊥OB交BO的延长线于点H,若∠EFD=α,现有以下结论:①∠COF=α;②∠AOH=180°﹣2α;③CH⊥CD;④∠OCH=2α﹣90°.其中正确的是__(填序号).
16.如图,在△ABC中,AD平分∠BAC,交BC于点D,BE⊥AD于E,AB=6,AC=14,∠ABC=3∠C,则BE=____.
17.如图,已知 O 为△ABC 三边垂直平分线的交点,且∠A=50°,则∠BOC 的度数为_____度.
18.已知:如图,ABC中,∠ACB=90°,AC=BC=,ABD是等边三角形,则CD的长度为______.
19.如图,△ABC是等边三角形,边长为2,AD是BC边上的高.E是AC边中点,点P是AD上的一个动点,则PC+PE的最小值是_______ ,此时∠CPE的度数是_______.
20.如图,在中,,且,,则的度数为______.
21.如图,已知,AB的垂直平分线交AB于D,交BC于E,AC的垂直平分线交AC于F,交BC于G,若,,,则的面积为______.
22.如图,在长方形中,,,点是边上一点,且,点是边上一动点,连接、.给出下列结论:
①;
②当时,;
③当时,平分;
④若,则.其中正确的是______.
三、解答题
23.如图,在中,,点D是BC的中点,连接AD,,BE分别交AC,AD于点E、,若,求AF的长度.
24.如图,ABC中,AC=2AB=6,BC=.AC的垂直平分线分别交AC,BC于点D,E.
(1)求BE的长;
(2)延长DE交AB的延长线于点F,连接CF.若M是DF上一动点,N是CF上一动点,请直接写出CM+MN的最小值为 .
25.在中,,在的外部作等边三角形,E为的中点,连接并延长交于点F,连接.
(1)如图1,若,求和的度数;
(2)如图2,的平分线交于点M,交于点N,连接.
①补全图2;
②若,求证:.
参考答案
1.A
【分析】作点A关于x轴的对称点A',连接A'P,则AP=A'P,当A',P,D在同一直线上时,AP+DP的最小值等于A'D的长,依据待定系数法即可得到直线A'D的解析式,进而得出点P的坐标为.
解:如图所示,作点A关于x轴的对称点A',连接A'P,则AP=A'P,
∴AP+DP=A'P+DP,
当A',P,D在同一直线上时,AP+DP的最小值等于A'D的长,
∵AC=BC=2,AB的中点为D,
∴A(0,2),B(2,0),D(1,1),A'(0,-2),
设直线A'D的解析式为y=kx+b(k≠0),则
,
解得:,
∴y=3x2,
当y=0时,x=,
∴点P的坐标为(,0),
故选:A.
2.C
【分析】易证△ACE≌△DCB,可得①正确;即可求得∠AOB=120°,可得③错误;再证明△ACM≌△DCN,可得②④正确和CM=CN,即可证明⑤正确;即可解题.
解:∵和都是等边三角形
∵∠ACD=∠BCE=60°,
∴∠DCE=60°,
在△ACE和△DCB中,
,
∴△ACE≌△DCB(SAS),
∴∠BDC=∠EAC,DB=AE,①正确;
∠CBD=∠AEC,
∵∠AOB=180°−∠OAB−∠DBC,
∴∠AOB=180°−∠AEC−∠OAB=120°,③错误;
在△ACM和△DCN中,
,
∴△ACM≌△DCN(ASA),
∴AM=DN,④正确;
∠AMC=∠DNC,②正确;
CM=CN,
∵∠ACD=∠BCE=60°,
∴∠MCN=180°-∠ACD-∠BCE =60°,
∴△CMN是等边三角形,⑤正确;
故有①②④⑤正确.
故选:C.
3.D
【分析】根据角平分线的性质定理判断A选项;证明△OPC≌△OPD判断B选项;根据△OPC≌△OPD即可判断C选项;证明△DPE≌△CPF判断D选项.
解:∵平分,于点,于点,
∴PC=PD,故A选项正确;
∵∠ODP=∠OCP=,
又∵OP=OP,PC=PD,
∴Rt△OPC≌Rt△OPD,
∴OC=OD,故B选项正确;
∵△OPC≌△OPD,
∴,故C选项正确;
∵∠PDE=∠PCF=,PD=PC,∠DPE=∠CPF,
∴△DPE≌△CPF,
∴PE=PF,
∵PF>PC,
∴PE>PC,故D选项错误;
故选:D.
4.A
【分析】利用AD=AC,求出∠ADC=∠C=,利用AD=AB,即可求得∠B=∠BAD.
解:∵AD=AC,
∴∠ADC=∠C,
∵,
∴∠ADC=∠C=,
∵AD=AB,
∴∠B=∠BAD,
故选:A.
5.A
【分析】根据中垂线的性质可得DA=DB,设∠A=x,则∠ABD=x,结合等腰三角形的性质以及三角形内角和定理,列出方程,即可求解.
解:又作图可知:EF是AB的垂直平分线,
∴DA=DB,
∴∠A=∠ABD,
设∠A=x,则∠ABD=x,
∵,
∴∠ABC=x+15°,
∵AB=AC,
∴∠C=∠ABC=x+15°,
∴2(x+15°)+x=180°,
∴x=50°,
故选A.
【点拨】
本题主要考查等腰三角形的性质,中垂线的性质以及三角形内角和定理,掌握中垂线的性质定理以及方程思想,是解题的关键.
6.B
【分析】过点O作MN,MN⊥AB于M,证明MN⊥CD,则MN的长度是AB和CD之间的距离;然后根据角平分线的性质,分别求出OM、ON的长度,再把它们求和即可.
解:如图,过点O作MN,MN⊥AB于M,交CD于N,
∵AB∥CD,
∴MN⊥CD,
∵AO是∠BAC的平分线,OM⊥AB,OE⊥AC,OE=3cm,
∴OM=OE=3cm,
∵CO是∠ACD的平分线,OE⊥AC,ON⊥CD,
∴ON=OE=3cm,
∴MN=OM+ON=6cm,
即AB与CD之间的距离是6cm,
故选B
7.D
【分析】①由等腰直角三角形的性质可得出结论;
②证明△ADE≌△BCE,可得∠AEC=∠DEB,即可求得∠AED=∠BEG,即可解题;
③证明△AEF≌△BED即可;
④AE≠DE,故④不正确;
⑤易证△FDC是等腰直角三角形,则CE=EF,S△AEF=S△ACE,由△AEF≌△BED,可知S△BDE=S△ACE,所以S△BDE=S△ACE.
解:①∵AD为△ABC的高线,
∴∠CBE+∠ABE+∠BAD=90°,
∵Rt△ABE是等腰直角三角形,
∴∠ABE=∠BAE=∠BAD+∠DAE=45°,AE=BE,
∴∠CBE+∠BAD=45°,
∴∠DAE=∠CBE,
故①正确
②在△DAE和△CBE中,
,
∴△ADE≌△BCE(SAS);
∴∠EDA=∠ECB,
∵∠ADE+∠EDC=90°,
∴∠EDC+∠ECB=90°,
∴∠DEC=90°,
∴CE⊥DE;
故②正确;
③∵∠BDE=∠ADB+∠ADE,∠AFE=∠ADC+∠ECD,
∴∠BDE=∠AFE,
∵∠BED+∠BEF=∠AEF+∠BEF=90°,
∴∠BED=∠AEF,
在△AEF和△BED中,
,
∴△AEF≌△BED(AAS),
∴BD=AF;
故③正确;
④∵AE≠DE,
∴△ADE不是等腰三角形,
⑤∵AD=BC,BD=AF,
∴CD=DF,
∵AD⊥BC,
∴△FDC是等腰直角三角形,
∵DE⊥CE,
∴EF=CE,
∴S△AEF=S△ACE,
∵△AEF≌△BED,
∴S△AEF=S△BED,
∴S△BDE=S△ACE.
故⑤正确;
故选:D.
8.A
【分析】
由△AEC≌△BED可知:EC=ED,∠C=∠BDE,∠BED=∠AEC,根据等腰三角形的性质即可知∠C的度数,从而可求出∠ADB的度数.
解:∵△AEC≌△BED,
∴EC=ED,∠C=∠BDE,∠BED=∠AEC,
∴∠BEO+∠AED=∠CED+∠AED,
∴∠BEO=∠CED,
∵∠AED=30°,∠BEC=120°,
∴∠BEO=∠CED==45°,
在△EDC中,
∵EC=ED,∠CED=45°,
∴∠C=∠EDC=67.5°,
∴∠BDE=∠C=67.5°,
∴∠ADB=180°-∠BDE-∠EDC=180°-67.5°-67.5°=45°,
故选A.
9.B
【分析】根据线段垂直平分线性质得出 AD = DC ,求出和 AB + BC 的长,即可求出答案.
解: DE 是 AC 的垂直平分线,AE=3cm,.
AC=2AE=6cm,AD = DC ,
△ ABD 的周长为13cm,
AB + BD +AD=13cm,
AB + BD + DC = AB +BC=13cm
△ ABC 的周长为 AB + BC +AC=13cm+6cm=19cm,
故选 B.
10.D
【分析】要求运动后得到的等腰三角形的腰长,首先要求出动点所运动的时间.我们可以设M、N运动的时间为x秒.
解:设M、N运动的时间为x秒.
当是以为底的等腰三角形时,
即,解得.
∴腰长为
故选D.
11.D
【分析】由偶次方的非负性质得出a-b=0,a-c=0,b-c=0,得出a=b=c,即可得出结论.
解:∵,
∴a-b=0,a-c=0,b-c=0,
∴a=b,a=c,b=c,
∴a=b=c,
∴这个三角形是等边三角形;
故选:D.
12.A
【分析】连接CN,与AD交于点M,连接BM,此时BM+MN取得最小值,由AD为∠BAC的角平分线,利用三线合一得到AD⊥BC,且平分BC,可得出BM=CM,由BM+MN=CM+MN=CN,可得出CN的长为最小值,利用等边三角形的性质及勾股定理求出即可.
解:如图,连接CN,与AD交于点M,此时BM+MN取得最小值,
∵AD为∠BAC的角平分线,等边△ABC
∴AD⊥BC,且平分BC,
∴AD为BC的垂直平分线,
∴CM=BM,
∴BM+MN=CM+MN=CN,即最小值为CN的长,
∵△ABC为等边三角形,且AB=2,AN=1,
∴CN为AB边上的中线,
∴CN⊥AB,
在Rt△ACN中,AC=AB=2,AN=1,
根据勾股定理得:,
故选:A.
13.C
【分析】如图,点N关于OB的对称点N′(-1,0),过点N′作N′P⊥AB交OB于M,则PN′=PM+MN的最小值,根据直线AB的解析式为y=-x+4,得到直线N′P的解析式为y=x+1,得到,推出△PAN′是等腰直角三角形,于是得到结论.
解:如图,点N关于OB的对称点N′(-1,0),过点N′作N′P⊥AB交OB于M,
则PN′=PM+MN的最小值,
∵直线AB的解析式为y=-x+4,
∴A(4,0),B(0,4),
∴直线N′P的解析式为y=x+1,
由 解得
,
∵A(4,0),B(0,4),
∴OA=OB,
∴∠BAO=45°,
∴△PAN′是等腰直角三角形,
∵AN′=4+1=5,
∴
∴PM+MN的最小值是
故选:C
14.B
【分析】过点E作于M,于N,于H,如图,先计算出,则AE平分,根据角平分线的性质得,再由CE平分得到,则,于是根据角平分线定理的逆定理可判断DE平分,再根据三角形外角性质解答即可.
解:过点E作于M,于N,于H,如图,
,,
,
平分,
,
平分,
,
,
平分,
,
由三角形外角可得:,
,
,
而,
,
故选:B.
15.①②③④
解:∵CD∥OB,∠EFD=α,
∴∠EOB=∠EFD=α,
∵OE平分∠AOB,
∴∠COF=∠EOB=α,故①正确;
∠AOB=2α,
∵∠AOB+∠AOH=180°,
∴∠AOH=180°﹣2α,故②正确;
∵CD∥OB,CH⊥OB,
∴CH⊥CD,故③正确;
∴∠HCO+∠HOC=90°,∠AOB+∠HOC=180°,
∴∠OCH=2α﹣90°,故④正确.
故答案为:①②③④.
16.
【分析】如图,延长 交于 证明 可得 再求解 再证明: 可得 从而可得答案.
解:如图,延长 交于
AD平分∠BAC,
故答案为:
17.100【分析】连接AO延长交BC于D,根据线段垂直平分线的性质可得OB=OA=OC,再根据等腰三角形的等边对等角和三角形的外角性质可得∠BOC=2∠A,即可求解.
解:连接AO延长交BC于D,
∵O 为△ABC 三边垂直平分线的交点,
∴OB=OA=OC,
∴∠OBA=∠OAB,∠OCA=∠OAC,
∵∠BOD=∠OBA+∠OAB=2∠OAB,∠COD=∠OCA+∠OAC=2∠OAC,
∴∠BOC=∠BOD+∠COD=2∠OAB+2∠OAC=2∠BAC,
∵∠BAC=50°,
∴∠BOC=100°.
故答案为:100.
18.
解:∵∠ACB=90°,AC=BC=,
∴AB=,∠CAB=∠CBA=45°,
∵ABD是等边三角形,
∴AB=AD=BD=2,∠DAB=∠ABD=60°,
∵AC=BC,AD=BD,
∴AB⊥CD于E,且AE=BE=1,
在Rt△AEC中,∠AEC=90°,∠EAC=45°,
∴∠EAC=∠ACE=45°,
∴AE=CE=1,
在Rt△AED中,∠AED=90°,AD=2,AE=1,
∴DE=,
∴CD=.
故答案为.
【点拨】本题考查了勾股定理,等腰直角三角形的性质,等边三角形的性质,线段垂直平分线的性质等知识.运用勾股定理求出DE是解决本题的关键.
19. 60°
解:作点E关于AD的对称点F,然后连接CF,交AD于点H,连接HE,如图所示:
∵△ABC是等边三角形,
∴AB=AC=BC,∠B=∠ACB=∠BAC=60°,
∵AD⊥BC,
∴AD平分∠BAC,BD=DC,
∵点E是AC的中点,AD垂直平分EF,
∴点F是AB的中点,
∴CF⊥AB,CF平分∠ACB,
∴∠BCF=30°,
∴当点P与点H重合时,根据轴对称的性质及两点之间线段最短可得此时PC+PE为最小值,即为CF的长,
∵BC=2,
∴BF=1,
在Rt△CBF中,,
∴PC+PE的最小值为;
∴∠DHC=∠FHP=60°,
∵AD垂直平分EF,
∴FH=HE,
∴∠FHP=∠PHE=60°,
∴∠CHE=60°,即为∠CPE=60°;
故答案为;60°.
【点拨】本题主要考查勾股定理、等边三角形的性质及轴对称的性质,熟练掌握勾股定理、等边三角形的性质及轴对称的性质是解题的关键.
20.120°
解:设∠ABC=,
∴.
∵,,
∴,,
∴,
∴,
∴,
∴,
∴,
故答案为:120°.
【点拨】本题考查了三角形内角和定理,等腰三角形的性质等知识,解题的关键是熟练掌握基本知识,属于中考常考题型.
21.18
【分析】连接AE、AG,根据中垂线的性质,求出AE,AG的长,结合勾股定理的逆定理,推出,进而即可求解.
解:连接AE、AG
∵DE垂直平分AB,
∴,
∵FG垂直平分AC,
∴,
∵,,,
∴,
在中,,,,
∴为直角三角形,
∴,
∴.
故答案是:18
【点拨】
本题主要考查垂直平分线的性质定理以及勾股定理的逆定理,掌握中垂线的性质定理,添加合适的辅助线,是解题的关键.
22.①②③④
【分析】
设BE=x,则=8-x,利用勾股定理列出方程即可判断①;利用SAS证出△AEP≌△CPE,即可证出∠AEP=∠CPE,从而判断②;过点E作EH⊥AD于H,利用勾股定理求出PE,从而得出PA=PE,利用等边对等角可得∠PAE=∠PEA,再根据平行线的性质可得∠AEB=∠PAE,从而判断③;根据三角形的内角和定理即可判断④.
解:设BE=x,则=8-x,
在Rt△ABE中,AB2+BE2=AE2
∴42+x2=(8-x)2
解得:x=3
即BE=3,故①正确;
∴BE=EC=5
若
∴AP=CE,
∵四边形ABCD为长方形
∴AD∥BC
∴∠APE=∠CEP
∵PE=EP
∴△AEP≌△CPE
∴∠AEP=∠CPE
∴,故②正确;
当时,过点E作EH⊥AD于H,
∴AH=BE=3,HE=AB=4
∴PH=AP-AH=
∴PE==
∴PA=PE
∴∠PAE=∠PEA
∵AD∥BC
∴∠AEB=∠PAE,
∴∠AEB=∠PEA
∴平分,故③正确;
∵∠BPC=180°-∠PCB-∠PBE
∠PEC=180°-∠PCB-∠EPC
∵
∴,故④正确;
综上:正确的有①②③④
故答案为:①②③④.
【点拨】此题考查的是勾股定理、全等三角形的判定及性质、等腰三角形的性质、平行线的判定及性质和三角形内角和定理的应用,掌握勾股定理、全等三角形的判定及性质、平行线的判定及性质和三角形内角和定理是解题关键.
23.
【分析】根据点D是BC的中点得到BD=5 ,由勾股定理计算可得AD的长,由等腰直角三角形性质得DF=5,最后由线段的差可得结论.
解:,
,
,
,
中,,
,
中,,
是等腰直角三角形,
,
.
【点拨】本题主要考查的是等腰三角形的性质,勾股定理,等腰直角三角形,结合题干中条件找出对应量是关键.
24.(1);(2)
【分析】
(1)利用勾股定理逆定理可得ABC是直角三角形,,连接AE,根据线段垂直平分线的性质可得,在中利用勾股定理列出方程即可求解;
(2)根据题意画出图形,若使的值最小,则A,M,N共线,且,利用全等三角形的判定与性质即可求解.
解:(1)连接AE,
,
∵,,
∴,
∴ABC是直角三角形,,
∵DE垂直平分AC,
∴,
在中,,即,
∴,解得;
(2)∵DE垂直平分AC,M是DF上一动点,
∴,
∴,
若使的值最小,则A,M,N共线,且,如图,
,
在和中,
,
∴≌,
∴.
【点拨】本题考查勾股定理逆定理、全等三角形的判定与性质、线段垂直平分线的性质,灵活运用以上基本性质定理是解题的关键.
25.(1),;(2)①作图见解析;②见解析
【分析】(1)结合等腰三角形和等边三角形的性质,可得∠ABD=∠ADB,从而求解出角度后,再计算∠BDF即可;
(2)①根据尺规作图作角平分线的方法画出的平分线即可;
②设∠ACM=∠BCM=α,由AB=AC,推出∠ABC=∠ACB=2α,可得∠NAC=∠NCA=α,∠DAN=60°+α,由△ABN≌△ADN(SSS),推出∠ABN=∠ADN=30°,∠BAN=∠DAN=60°+α,∠BAC=60°+2α,在△ABC中,根据∠BAC+∠ACB+∠ABC=180°,构建方程求出α,再证明∠MNB=∠MBN即可解决问题.
解:(1)∵,为等边三角形,
∴,,,
∵,
∴,
∴,
又∵E为的中点,
∴由“三线合一”知,,
∴;
(2)①如图所示:利用尺规作图的方法得到CP,交于点M,交于点N;
②如图所示,连接,
∵平分,
∴设,
∵,
∴,
在等边三角形中,
∵为的中点,
∴,
∴,
∴,
∴,
在和中,
∴,
∴,,
∴,
在中,,
∴,
∴,
∴,
∴,
∴,
∴.
【点拨】本题考查全等三角形的判定和性质,等边三角形的性质,等腰三角形的判定和性质等知识,解题的关键是灵活运用各类图形的性质进行综合分析.
浙教版八年级数学下册基础知识专项讲练 专题1.13 二次根式(全章复习与巩固)(培优篇)(含答案): 这是一份浙教版八年级数学下册基础知识专项讲练 专题1.13 二次根式(全章复习与巩固)(培优篇)(含答案),共17页。试卷主要包含了单选题,填空题,解答题等内容,欢迎下载使用。
湘教版七年级下册5.2 旋转达标测试: 这是一份湘教版七年级下册<a href="/sx/tb_c95260_t7/?tag_id=28" target="_blank">5.2 旋转达标测试</a>,共35页。试卷主要包含了单选题,填空题,解答题等内容,欢迎下载使用。
初中浙教版第一章 二次根式1.1 二次根式课堂检测: 这是一份初中浙教版<a href="/sx/tb_c12201_t7/?tag_id=28" target="_blank">第一章 二次根式1.1 二次根式课堂检测</a>,共17页。试卷主要包含了单选题,填空题,解答题等内容,欢迎下载使用。












