（全国通用）2022年中考数学命题点及重难题型分类突破练 模型十 主从联动（原卷版+解析版）

这是一份（全国通用）2022年中考数学命题点及重难题型分类突破练 模型十 主从联动（原卷版+解析版），文件包含全国通用2022年中考数学命题点及重难题型分类突破练模型十主从联动解析版docx、全国通用2022年中考数学命题点及重难题型分类突破练模型十主从联动原卷版docx等2份试卷配套教学资源，其中试卷共26页， 欢迎下载使用。
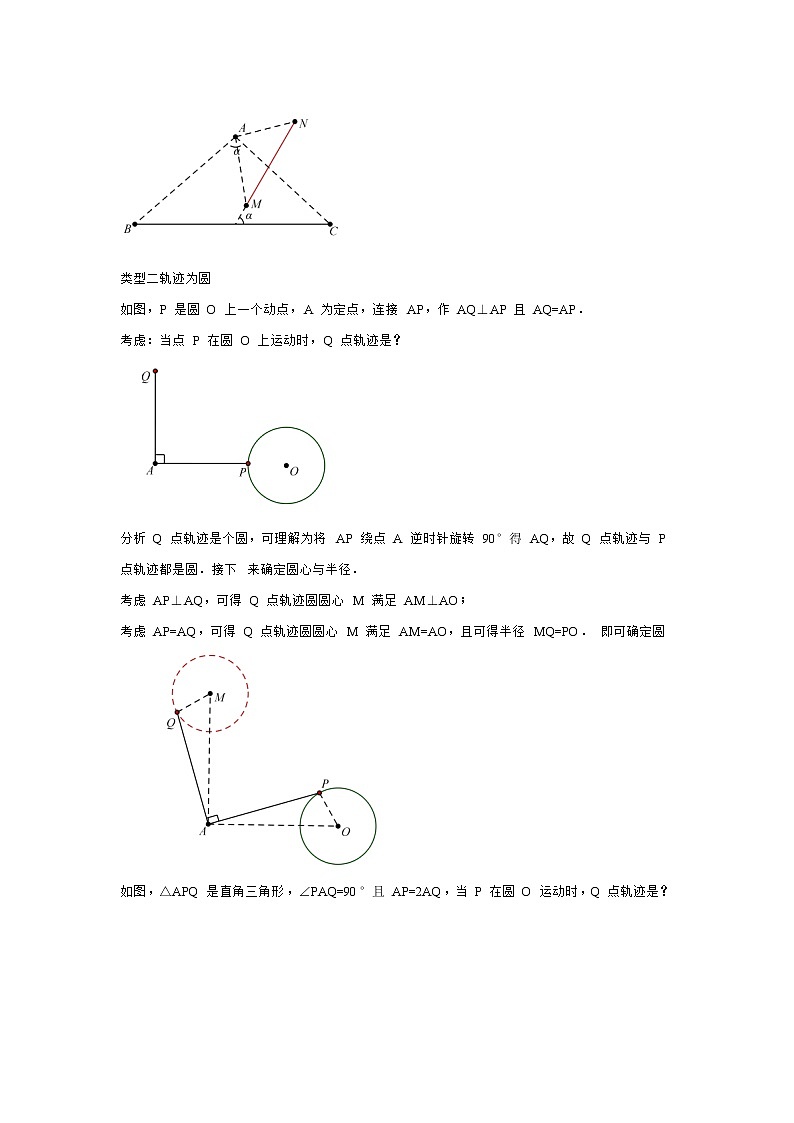
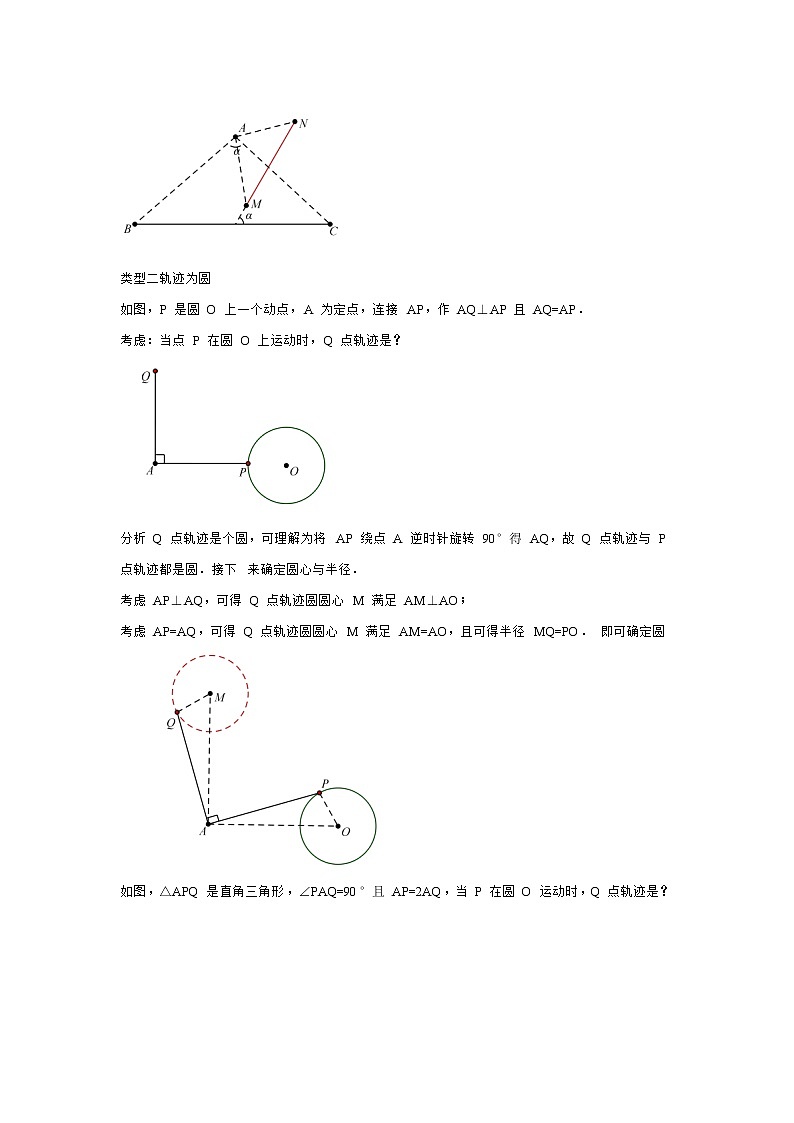
模型十主从联动         【基础模型】【基本模型】类型一轨迹为直线引例：如图，P 是直线 BC 上一动点，连接 AP，取 AP 中点 Q，当点 P 在 BC 上运动时，Q 点轨迹 是？ 分析当 P 点轨迹是直线时，Q 点轨迹也是一条直线． 可以这样理解：分别过 A、Q 向 BC 作垂线，垂足分别为 M、N，在运动过程中，因为 AP=2AQ， 所以 QN 始终为 AM 的一半，即 Q 点到 BC 的距离是定值，故 Q 点轨迹引例如图，△APQ 是等腰直角三角形，∠PAQ=90°且 AP=AQ，当点 P 在直线 BC 上运动时，求 Q 点轨迹？分析当 AP 与 AQ 夹角固定且 AP:AQ 为定值的话，P、Q 轨迹是同一种图形．当确定轨迹是线段的时候，可以任取两个时刻的 Q 点的位置，连线即可，比如 Q 点的起始位置和 终点位置，连接即得 Q 点轨迹线段 模型总结 必要条件： 主动点、从动点与定点连线的夹角是定量（∠PAQ 是定值）； 主动点、从动点到定点的距离之比是定量（AP:AQ 是定值）． 结论： P、Q 两点轨迹所在直线的夹角等于∠PAQ（当∠PAQ≤90°时，∠PAQ 等于 MN 与 BC 夹角）P、Q 两点轨迹长度之比等于 AP:AQ（由△ABC∽△AMN，可得 AP:AQ=BC:M类型二轨迹为圆如图，P 是圆 O 上一个动点，A 为定点，连接 AP，作 AQ⊥AP 且 AQ=AP． 考虑：当点 P 在圆 O 上运动时，Q 点轨迹是？ 分析 Q 点轨迹是个圆，可理解为将 AP 绕点 A 逆时针旋转 90°得 AQ，故 Q 点轨迹与 P 点轨迹都是圆．接下 来确定圆心与半径． 考虑 AP⊥AQ，可得 Q 点轨迹圆圆心 M 满足 AM⊥AO； 考虑 AP=AQ，可得 Q 点轨迹圆圆心 M 满足 AM=AO，且可得半径 MQ=PO． 即可确定圆如图，△APQ 是直角三角形，∠PAQ=90°且 AP=2AQ，当 P 在圆 O 运动时，Q 点轨迹是？ 分析考虑 AP⊥AQ，可得 Q 点轨迹圆圆心 M 满足 AM⊥AO； 考虑 AP:AQ=2:1，可得 Q 点轨迹圆圆心 M 满足 AO:AM=2:1． 即可确定圆 M 位置，任意时刻均有△APO∽△AQM，且相似比为 2．模型总结 为了便于区分动点 P、Q，可称点 P 为“主动点”，点 Q 为“从动点”． 此类问题的必要条件：两个定量 主动点、从动点与定点连线的夹角是定量（∠PAQ 是定值）； 主动点、从动点到定点的距离之比是定量（AP:AQ 是定值）结论（1）主、从动点与定点连线的夹角等于两圆心与定点连线的夹角： ∠PAQ=∠OAM； （2）主、从动点与定点的距离之比等于两圆心到定点的距离之比： AP:AQ=AO:AM ，也等于两圆半径之比． 按以上两点即可确定从动点轨迹圆，Q 与 P 的关系相当于旋转+伸缩． 古人云：种瓜得瓜，种豆得豆．“种”圆得圆，“种”线得线，谓之“瓜豆原理”． 思考 1：如图，P 是圆 O 上一个动点，A 为定点，连接 AP，以 AP 为一边作等边△APQ． 考虑：当点 P 在圆分析 Q 点满足（1）∠PAQ=60°；（2）AP=AQ，故 Q 点轨迹是个圆： 考虑∠PAQ=60°，可得 Q 点轨迹圆圆心 M 满足∠MAO=60°； 考虑 AP=AQ，可得 Q 点轨迹圆圆心 M 满足 AM=AO，且可得半径 MQ=PO． 即可确定圆 M 位置，任意时刻均有△APO≌△AQM小结可以理解 AQ 由 AP 旋转得来，故圆 M 亦由圆 O 旋转得来，旋转角度与缩放比例均等于 AP 与 AQ 的位 置和数量关系思考 2 如图，P 是圆 O 上一个动点，A 为定点，连接 AP，以 AP 为斜边作等腰直角△APQ． 考虑：当点分析 Q 点满足（1）∠PAQ=45°；（2）AP:AQ= ：1，故 Q 点轨迹是个圆． 连接 AO，构造∠OAM=45°且 AO:AM= ：1．M 点即为 Q 点轨迹圆圆心，此时任意时刻均有△AOP∽△ AMQ．即可确定点 Q 的轨迹圆【强化训练】1、如图，正方形ABCD的边长为4，E为BC上一点，且BE=1，F为AB边上的一个动点，连接EF，以EF为边向右侧作等边△EFG，连接CG，则CG的最小值为　　．【分析】同样是作等边三角形，区别于上一题求动点路径长，本题是求CG最小值，可以将F点看成是由点B向点A运动，由此作出G点轨迹：考虑到F点轨迹是线段，故G点轨迹也是线段，取起点和终点即可确定线段位置，初始时刻G点在位置，最终G点在位置（不一定在CD边），即为G点运动轨迹．CG最小值即当CG⊥的时候取到，作CH⊥于点H，CH即为所求的最小值．根据模型可知：与AB夹角为60°，故⊥．过点E作EF⊥CH于点F，则HF==1，CF=，所以CH=，因此CG的最小值为．2、如图，矩形中，，，点是矩形内一动点，且，则的最小值为_____．【答案】【详解】为矩形，又点到的距离与到的距离相等，即点线段垂直平分线上，连接，交与点，此时的值最小，且故答案为：3、如图，已知等边三角形ABC边长为2，两顶点A、B分别在平面直角坐标系的x轴负半轴、轴的正半轴上滑动，点C在第四象限，连接OC，则线段OC长的最小值是（　　）A．1 B．3 C．3 D．【答案】B【详解】解：如图所示：过点C作CE⊥AB于点E，连接OE，∵△ABC是等边三角形，∴CE=AC×sin60°=，AE=BE，∵∠AOB=90°，∴EOAB，∴EC-OE≥OC，∴当点C，O，E在一条直线上，此时OC最短，故OC的最小值为：OC＝CE﹣EO＝3故选B．4、如图，在中，，，，点O是AB的三等分点，半圆O与AC相切，M，N分别是BC与半圆弧上的动点，则MN的最小值和最大值之和是（    ）A．5 B．6 C．7 D．8【答案】B【详解】如图，设⊙O与AC相切于点D，连接OD，作垂足为P交⊙O于F，此时垂线段OP最短，PF最小值为，∵，，∴∵，∴∵点O是AB的三等分点，∴，，∴，∵⊙O与AC相切于点D，∴，∴，∴，∴，∴MN最小值为，如图，当N在AB边上时，M与B重合时，MN经过圆心，经过圆心的弦最长，MN最大值，,∴MN长的最大值与最小值的和是6．故选B．5、如图，∠MON=90°，矩形ABCD的顶点A、B分别在边OM、ON上，当B在边ON上运动时，A随之在OM上运动，矩形ABCD的形状保持不变，其中AB=4，BC=2.运动过程中点D到点O的最大距离是______．【答案】+2【详解】如图，取AB的中点E，连接OE、DE、OD，∵OD≤OE+DE，∴当O、D、E三点共线时，点D到点O的距离最大，此时，∵AB=4，BC=2，∴OE=AE=AB=2，DE==，∴OD的最大值为：+2，故答案为+2.6、如图，在矩形ABCD中，AB=4，AD=6，E是AB边的中点，F是线段BC上的动点，将ΔEBF沿EF所在直线折叠得到ΔEB' F，连接B' D，则B' D的最小值是_____．【答案】.【详解】如图所示点B'在以E为圆心EA为半径的圆上运动，当D、B'、E共线时，B'D的值最小，根据折叠的性质，△EBF≌△EB'F，∴∠B=∠EB'F，EB'=EB．∵E是AB边的中点，AB=4，∴AE=EB'=2．∵AD=6，∴DE2，∴B'D=22．故答案为22．7、如图，过抛物线上一点A作轴的平行线，交抛物线于另一点B，交轴于点C，已知点A的横坐标为．（1）求抛物线的对称轴和点B的坐标；（2）在AB上任取一点P，连结OP，作点C关于直线OP的对称点D；①连结BD，求BD的最小值；②当点D落在抛物线的对称轴上，且在轴上方时，求直线PD的函数表达式．【答案】(1)x=4；B（10，5）．（2）①．②y=﹣x+．【详解】（1）由题意A（﹣2，5），对称轴x=﹣=4，∵A、B关于对称轴对称，∴B（10，5）．（2）①如图1中，由题意点D在以O为圆心OC为半径的圆上，∴当O、D、B共线时，BD的最小值=OB﹣OD=．②如图2中，图2当点D在对称轴上时，在Rt△ODE中，OD=OC=5，OE=4，∴DE==3，∴点D的坐标为（4，3）．设PC=PD=x，在Rt△PDK中，x2=（4﹣x）2+22，∴x=，∴P（，5），∴直线PD的解析式为y=﹣x+．8、如图，等边三角形ABC的边长为4，点D是直线AB上一点．将线段CD绕点D顺时针旋转60°得到线段DE，连结BE．（1）若点D在AB边上（不与A，B重合）请依题意补全图并证明AD=BE；（2）连接AE，当AE的长最小时，求CD的长． 【答案】（1）见解析；（2）【详解】解：（1）补全图形如图1所示，AD=BE，理由如下：
∵△ABC是等边三角形，
∴AB=BC=AC，∠A=∠B=60°，
由旋转的性质得：∠ACB=∠DCE=60°，CD=CE，
∴∠ACD=∠BCE，
∴△ACD≌△BCE（SAS），
∴AD=BE．

（2）如图2，过点A作AF⊥EB交EB延长线于点F．
∵△ACD≌△BCE，
∴∠CBE=∠A=60°，
∴点E的运动轨迹是直线BE，
根据垂线段最短可知：当点E与F重合时，AE的值最小，
此时CD=CE=CF，
∵∠ACB=∠CBE=60°，
∴AC∥EF，
∵AF⊥BE，
∴AF⊥AC，在Rt△ACF中，
∴CF===，∴CD=CF=.