（全国通用）备战中考数学一轮复习专题讲义+强化训练 第二十一讲 特殊的平行四边形（强化训练）

这是一份（全国通用）备战中考数学一轮复习专题讲义+强化训练 第二十一讲 特殊的平行四边形（强化训练），文件包含全国通用备战2022年中考数学一轮复习专题第二十一讲特殊的平行四边形强化训练解析版docx、全国通用备战2022年中考数学一轮复习专题第二十一讲特殊的平行四边形强化训练原卷版docx等2份试卷配套教学资源，其中试卷共37页， 欢迎下载使用。
备战2022年中考数学一轮复习专题讲义+强化训练（全国通用）
第二十一讲 特殊平行四边形
考点一 特殊平行四边形中的翻折问题 2
考点二 菱形的性质与判定 8
考点三 矩形的性质与判定 8
考点四 正方形的性质与判定 22
















考点一 特殊平行四边形中的翻折问题

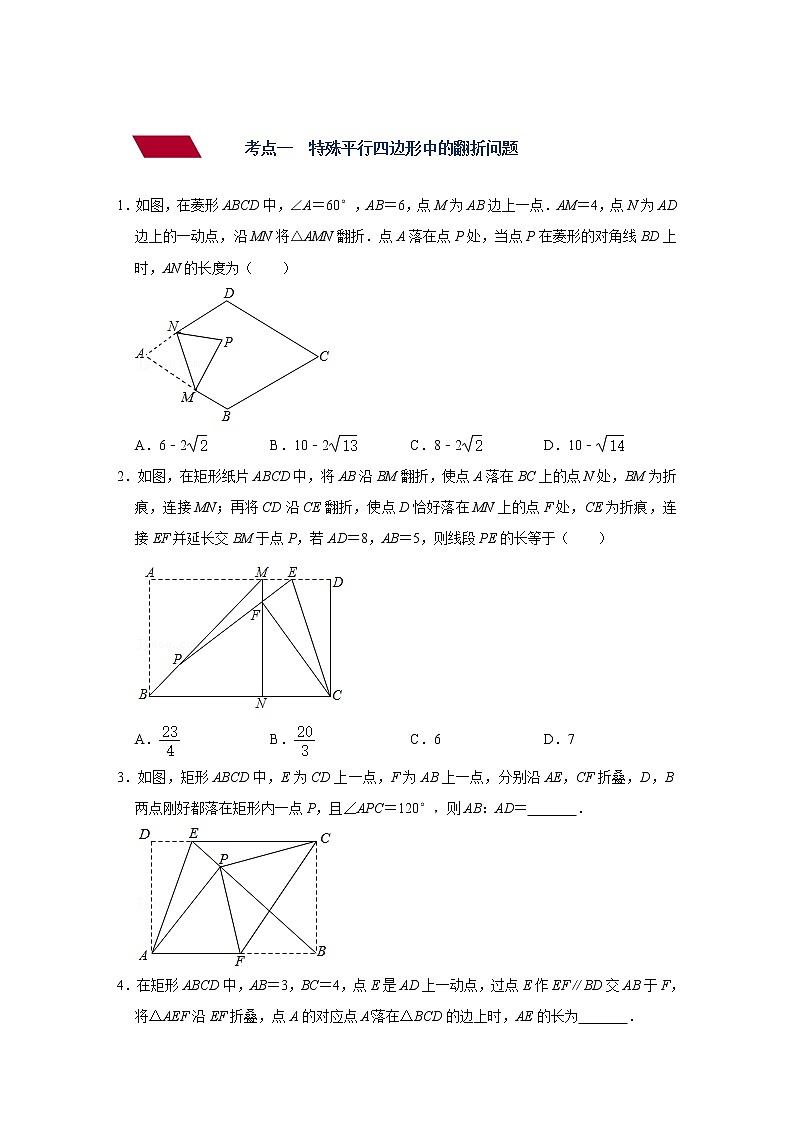
1．如图，在菱形ABCD中，∠A＝60°，AB＝6，点M为AB边上一点．AM＝4，点N为AD边上的一动点，沿MN将△AMN翻折．点A落在点P处，当点P在菱形的对角线BD上时，AN的长度为（　　）

A．6﹣2 B．10﹣2 C．8﹣2 D．10﹣
【解答】解：如图，

设AN＝x，
由折叠的性质得：PM＝AM＝4，PN＝AN＝x，∠MPN＝∠A＝60°，
∵AB＝6，
∴BM＝AB﹣AM＝2，
∵四边形ABCD是菱形，
∴∠ADC＝180°﹣60°＝120°，∠PDN＝∠MBP＝∠ADC＝60°，
∵∠BPN＝∠BPM+60°＝∠DNP+60°，
∴∠BPM＝∠DNP，
∴△PDN∽△MBP，
∴，即，
∴PD＝x，
∴＝，
解得：x＝10﹣2或10+2（不合题意舍去），
∴AN＝10﹣2，
故选：B．
2．如图，在矩形纸片ABCD中，将AB沿BM翻折，使点A落在BC上的点N处，BM为折痕，连接MN；再将CD沿CE翻折，使点D恰好落在MN上的点F处，CE为折痕，连接EF并延长交BM于点P，若AD＝8，AB＝5，则线段PE的长等于（　　）

A． B． C．6 D．7
【解答】解：过点P作PG⊥FN，PH⊥BN，垂足为G、H，

由折叠得：ABNM是正方形，AB＝BN＝NM＝MA＝5，
CD＝CF＝5，∠D＝∠CFE＝90°，ED＝EF，
∴NC＝MD＝8﹣5＝3，
在Rt△FNC中，FN＝＝4，
∴MF＝5﹣4＝1，
在Rt△MEF中，设EF＝x，则ME＝3﹣x，由勾股定理得，
12+（3﹣x）2＝x2，
解得：x＝，
∵∠CFN+∠PFG＝90°，∠PFG+∠FPG＝90°，
∴∠CFN＝∠FPG，
∵∠CNF＝∠PGF＝90°，
∴△FNC∽△PGF，
∴FG：PG：PF＝NC：FN：FC＝3：4：5，
设FG＝3m，则PG＝4m，PF＝5m，
∴GN＝PH＝BH＝4﹣3m，HN＝5﹣（4﹣3m）＝1+3m＝PG＝4m，
解得：m＝1，
∴PF＝5m＝5，
∴PE＝PF+FE＝5+＝，
故选：B．
3．如图，矩形ABCD中，E为CD上一点，F为AB上一点，分别沿AE，CF折叠，D，B两点刚好都落在矩形内一点P，且∠APC＝120°，则AB：AD＝　：1　．

【解答】解：如图，设AD＝BC＝x．过点P作PH⊥AC于H．

由翻折的性质可知，PA＝PC＝BC＝x，
∵∠APC＝120°，PH⊥AC，
∴AH＝CH，∠APH＝∠CPH＝60°，
∴AC＝2AH＝2•PA•sin60°＝x，
∵四边形ABCD是矩形，
∴∠D＝90°，
∴CD＝AB＝＝＝x，
∴＝＝，
故答案为：1．
4．在矩形ABCD中，AB＝3，BC＝4，点E是AD上一动点，过点E作EF∥BD交AB于F，将△AEF沿EF折叠，点A的对应点A'落在△BCD的边上时，AE的长为　2或　．

【解答】解：如图，当点A'落在BD上时，连接AA'交EF于H，

∵将△AEF沿EF折叠，
∴AH＝A'H，
∵EF∥BD，
∴，
∴AE＝DE＝AD＝2；
若点A'落在BC上时，
如图，当点A'落在BC上时，连接AA'交EF于点H，过点A'作A'N⊥AD于N，

∵A'N⊥AD，∠DAB＝∠ABC＝90°，
∴四边形ABCD是矩形，
∴AB＝A'N＝3，AN＝A'B，
∵AB＝3，BC＝4＝AD，
∴BD＝＝＝5，
∵将△AEF沿EF折叠，
∴AA'⊥EF，AE＝A'E，AF＝A'F，
∵EF∥BD，
∴AA'⊥BD，
∴∠AA'B+∠A'BD＝90°，
又∵∠ABD+∠A'BD＝90°，
∴∠ABD＝∠AA'B，
∴tan∠ABD＝tan∠AA'B＝＝，
∴BA'＝＝，
∵A'E2＝A'N2+NE2，
∴AE2＝9+（AE﹣）2，
∴AE＝，
综上所述：AE＝2或，
故答案为：2或．
5．如图，在矩形ABCD中，AB＝6，BC＝，E为CD边上一点，将△BCE沿BE折叠，点C的对应点为点F，连接AF，若tan∠BAF＝，则CE＝　或　．

【解答】解：当点F在AB上方时，
过点F作MN∥AD，交AB、CD分别于点M、N，则MN⊥AB，MN⊥CD，

由折叠得：EC＝EF，BC＝BF＝，∠C＝∠BFE＝90°，
∵tan∠BAF＝＝，
设FM＝x，则AM＝3x，BM＝6﹣3x，
在Rt△BFM中，由勾股定理得：BF2＝FM2+BM2，
∴x2+（6﹣3x）2＝10，
∴x＝1或x＝2.6（舍去）
∴FM＝1，BM＝3，
∴NF＝﹣1，
∵∠EFB＝90°，
∴∠NFE+∠BFM＝90°，∠NFE+△NEF＝90°，
∴∠NEF＝∠BFM，
又∵∠FNE＝∠BMF＝90°，
∴△ENF∽△FMB，
∴，
∴NE＝＝，
∵MN⊥AB，MN⊥CD，∠C＝90°，
∴四边形BCNM是矩形，
∴CN＝BM＝3，
∴CE＝3﹣＝，
当点F在AB下方时，

同理可求CE＝
故答案为：或．



考点二 菱形的性质与判定

6．菱形ABCD的对角线AC、BD相交于点O，过点B作BE⊥AB交AC于点E．已知点F是AB边上一点，且BF＝BE，过点F作PF⊥AB交BD延长线于点P，交AD于点Q．
（1）如图1，若F是AB的中点，且BE＝2，求PD的长；
（2）如图2，求证：AQ＝BE+PQ；
（3）如图3，在菱形ABCD中，已知∠BAD＝60°，AB＝6，点P是对角线上的动点，过点B作BM垂直直线AP于点M，点N是CD边上的动点，请直接写出+MN的最小值．


【解答】（1）解：如图1中，

∵四边形ABCD是菱形，
∴AC⊥BD，OB＝OD，
∵AF＝FB，BE＝BF＝2，
∴AB＝4，
∵BE⊥AB，PF⊥AB，
∴∠PFB＝∠ABE＝∠BOE＝90°，
∴∠ABO+∠EBO＝90°，∠EBO+∠AEB＝90°，
∴∠AEB＝∠PBF，
∴△ABE≌△PFB（ASA），
∴AE＝PB＝＝＝2，
∵S△AEB＝•AB•BE＝•AE•BO，
∴BO＝＝，
∴OD＝OB＝，
∴PD＝PB﹣BD＝2﹣﹣＝．

（2）证明：如图2中，连接DE，EQ，过点E作EK⊥QF于点K，作QJ∥BD交AB于点J，在AB上取一点T，使得PQ＝AT．

由（1）可知，△ABE≌△PFB，
∴AB＝PF，
∵AT＝PQ，
∴BT＝QF，
∵EK⊥PF，PF⊥AB，BE⊥AB，
∴∠EKF＝∠KFB＝∠FBE＝90°，
∴四边形BEKF是矩形，
∵BE＝BF，
∴四边形BEKF是正方形，
∴BF＝KF，
∴FT＝QK，
∵四边形ABCD是菱形，
∴△ABE，△ADE关于AC对称，
∴∠ABE＝∠ADE＝90°，EB＝ED，
∵∠EDQ＝∠EKQ＝90°，EQ＝EQ，EK＝EB＝ED，
∴Rt△EQK≌Rt△EQD（HL），
∴DQ＝BJ，
∵QJ∥BD，AD＝AB，
∴＝，
∴AQ＝AJ，
∴DQ＝BJ＝QK＝FJ，
∴TJ＝BF＝BE，
∴AQ＝AJ＝AT+TJ＝PA+BE．

（3）解：如图3中，取AB的中点O，连接OD，延长OD到J，使得DJ＝DC，连接CJ

∵BM⊥AP，
∴∠AMB＝90°，
∴点M在以AB为直径的圆上运动，
∵四边形ABCD是菱形，∠BAD＝60°，
∴△ABD是等边三角形，
∵AO＝OB，
∴OD⊥AB，
∵AB∥CD，
∴DJ⊥DC，
∵DJ＝DC，
∴△DJC是等腰直角三角形，
过点N作NW⊥CJ于点W，过点O作OW′⊥CJ于W′，交⊙O于点M′，交CD于点N′．
∵NW⊥CW，∠NCW＝45°，
∴NW＝CN，
∴MN+CN＝MN+NW，
∵OM+MN+NW≥OW′，
∴MN+CN的最小值＝OW′﹣OM，
∵△ADB是等边三角形，AB＝6，
∴OD＝3，DJ＝DC＝AB＝6，
∴OJ＝6+3，
∵△OJW′是等腰直角三角形，
∴OW′＝OJ＝3+，
∵OM′＝AB＝3，
∴OW′﹣OM′＝3+﹣3，
∴MN+CN的最小值为3+﹣3．
7．如图所示，在菱形ABCD中，AC是对角线，CD＝CE，连接DE．
（1）若AC＝16，CD＝10，求DE的长．
（2）G是BC上一点，若GC＝GF＝CH且CH⊥GF，垂足为P，求证：DH＝CF．

【解答】（1）解：连接BD交AC于K．
∵四边形ABCD是菱形，
∴AC⊥BD，AK＝CK＝8，
在Rt△AKD中，DK＝＝6，
∵CD＝CE，
∴EK＝CE﹣CK＝10﹣8＝2，
在Rt△DKE中，DE＝＝2．

（2）证明：过H作HQ⊥CD于Q，过G作GJ⊥CD于J．
∵CH⊥GF，
∴∠GJF＝∠CQH＝∠GPC＝90°，
∴∠QCH＝∠JGF，
∵CH＝GF，
∴△CQH≌△GJF（AAS），
∴QH＝JF，
∵GC＝GF，
∴∠QCH＝∠JGF＝∠CGJ，CJ＝FJ＝CF，
∵GC＝CH，
∴∠CHG＝∠CGH，
∴∠CDH+∠QCH＝∠HGJ+∠CGJ，
∴∠CDH＝∠HGJ，
∵∠GJF＝∠CQH＝∠GPC＝90°，
∴∠CDH＝∠HGJ＝45°，
∴DH＝QH，
∴DH＝2QH＝CF．

8．如图，在菱形ABCD中，其对角线AC、BD交于点O，以边CD为斜边构造Rt△CDE，连接OE．
（1）如图一，△CDE为等腰三角形，且∠ABC＝60°，OC＝2，求OE的长；
（2）如图一，若△CDE为等腰三角形，求证：OD+OC＝OE；
（3）如图二，若菱形的边长为，BD＝6，OE的中点为H，连接BH，求BH的最大值．

【解答】解：（1）如图一中，过点D作DH⊥OE于H．

∵四边形ABCD是菱形，
∴AC⊥BD，OC＝OA＝2，AB＝BC＝AD＝CD，
∵∠ABC＝∠ADC＝60°，
∴△ABC，△ADC都是等边三角形，
∴CD＝AC＝4，∠ACD＝60°，
∵ED＝EC，∠DEC＝90°，
∴∠DCE＝∠CDE＝45°，
∵∠DOC＝∠DEC＝90°，
∴∠DOC+∠DEC＝180°，
∴D，O，E，C四点共圆，
∴∠DOE＝∠DCE＝45°，∠DEO＝∠DCO＝60°，
在Rt△ODC中，OD＝CD•sin60°＝2
在Rt△ODH中，DH＝OH＝OD＝，
在Rt△DHE中，EH＝＝，
∴OE＝OH+EH＝+．

（2）如图一（1）中，过点E作EM⊥BD于M，EF⊥AC交AC的延长线于F．

∵∠EMO＝∠MOF＝∠F＝90°，
∴四边形EMOF是矩形，
∴∠MEF＝∠DEC＝90°，
∴∠DEM＝∠CEF，
∵ED＝EC，
∴△EMD≌△EFC（AAS），
∴EM＝EF，DM＝CF，
∴四边形EMOF是正方形，
∴OM＝OF＝EM＝EF，
∴OC+OD＝OF﹣CF+OM+DM＝2OM＝OE，
∴OC+OD＝OE．

（3）如图二中，取CD的中点F，连接OF，取OF的中点J，连接EF，JH，过点O作OM⊥BC于M，过点J作JN⊥BC交BC的延长线于N．

∵四边形ABCD是菱形，
∴AC⊥BD，OA＝OC，OD＝OB＝3，AD＝BC＝CD＝，
∴OA＝OC＝＝＝1，
∵DO＝OB，DF＝FC，
∴OF＝BC＝，OF∥BC，
∴OJ＝JF＝，
∵OM⊥BC，
∴S△OBC＝•OB•OC＝•BC•OM，
∴OM＝，BM＝＝＝，
∵OM⊥BC，JN⊥BC，
∴∠OMN＝∠JNM＝∠OJM＝90°，
∴四边形OMNJ是矩形，
∴OM＝JN＝，OJ＝MN＝，
∴BN＝BM+MN＝+＝，
∴BJ＝＝＝，
∵CF＝DF，∠DEC＝90°，
∴EF＝CD＝，
∵OH＝HE，OJ＝JF，
∴JH＝EF＝，
∵BH≤BJ+JH，
∴BH≤+，
∴BH的最大值为+．


考点三 矩形的性质与判定

9．如图1，在矩形ABCD中，∠ABC的平分线交AD于点E，连接CE．
（1）若BE＝4，CE＝，求AD的长；
（2）如图2，点F是BC上一点，且EF＝EC，过点C作CG⊥EF于点G，交BE于点H，求证：BH＝DE；
（3）如图3，在（2）的条件下，连接DG，当BE＝BC时，请直接写出的值．

【解答】（1）解：如图1中，

∵四边形ABCD是矩形，
∴∠ABC＝∠A＝∠D＝90°，AB＝CD，
∵BE平分∠ABC，
∴∠ABE＝45°，
∴∠ABE＝∠AEB＝45°，
∵BE＝4，
∴AB＝AE＝4，CD＝AB＝4，
在Rt△CED中，DE＝＝＝1，
∴AD＝AE+DE＝4+1＝5．

（2）证明：过点E作ET⊥BC于T，过点H作HR⊥BC于R．

∵∠A＝∠ABT＝∠BTE＝90°，
∴四边形ABTE是矩形，
∵AB＝AE，
∴四边形ABTE是正方形，
∴∠EBT＝∠BET＝45°，
∵EF＝EC，ET⊥CF，
∴FT＝TC，∠FET＝∠CET，∠EFC＝∠ECF，
∵CG⊥EF，
∴∠CGF＝∠ETC＝90°，
∴∠CFG+∠FCG＝90°，∠CET+∠ECT＝90°，
∴∠GCF＝∠CET，
∵∠CEH＝∠CET+∠BET＝45°+∠CET，∠CHB＝∠CBH+∠HCB＝45°+∠HCB，
∴∠CEH＝∠CHE，
∴CE＝CH，
∵HR⊥BC，
∴∠CRH＝∠ETC＝90°，
在△CRH和△ETC中，
，
∴△CRH≌△ETC（AAS），
∴HR＝CT，
∵∠D＝∠DCT＝∠ETC＝90°，
∴四边形DETC是矩形，
∴DE＝CT＝HR，
∵△BRH是等腰直角三角形，
∴BH＝HR＝DE．

（3）解：过点E作ET⊥BC于T，过点H作HR⊥BC于R，过点G作GM⊥AD于M，GN⊥CD于N．

设AB＝AE＝m，则BE＝BC＝m，
∴DE＝AD﹣AE＝m﹣m，
∴BH＝DE＝2m﹣m，
由（2）可知，∠CEH＝∠CHE＝∠BCE＝45°+∠BCH＝67.5°，
∴∠ECH＝45°，
∵CG⊥EG，
∴GC＝GE，
∵∠MGN＝∠EGC＝90°，
∴∠MGE＝∠NGC，
在△GME和△GNC中，
，
∴△GME≌△GNC（AAS），
∴GM＝GN，
∵GM⊥AD，GN⊥CD，
∴GD平分∠ADC，
∴∠CDG＝45°，
∵BE＝BC，∠CBE＝45°，
∴∠BCE＝67.5°，
∴∠BCH＝22.5°，
∵∠DCB＝90°，
∴∠DCG＝67.5°，
∴∠DGC＝180°﹣45°﹣67.5°＝67.5°，
∴∠DGC＝∠DCG，
∴DG＝DC＝m，
∴＝＝2﹣．
10．如图，在矩形ABCD中，点P为CB延长线上一点，连接AP．
（1）如图1，以CD为底向内作等腰△CDE，延长DE恰好交CB延长线于点P，交AB于点F，若AF＝5BF，EC＝6，求EF的长；
（2）如图2，若∠APB＝60°，AB＝AD，以CD为边向外作等边△CDF，连接AF，DE平分∠ADC交AF于点E，连接PE．求证：PA+PC＝PE．
【解答】（1）解：∵CE＝DE，
∴∠ECD＝∠EDC，
∵∠DPC+∠PDC＝90°，
∠ECP+∠ECD＝90°，
∴∠EPC＝∠ECP，
∴PE＝CE＝6，
∴PD＝12，
∵PB∥AD，
∴，
∴PF＝2，DF＝10，
∴EF＝4；
（2）证明：连接CE，

∵四边形ABCD是矩形，AB＝AD，
∴四边形ABCD是正方形，
∴AD＝CD，∠ADC＝90°，
∵△CDF是等边三角形，
∴∠CDF＝60°，AD＝DF，
∴∠DAF＝15°，
∵DE平分∠ADC，
∴∠ADE＝∠CDE＝45°，
∴∠AED＝120°，
又∵DE＝DE，
在△ADE和△CDE中，
，
△ADE≌△CDE（SAS），
∴∠AED＝∠CED＝∠AEC＝120°，AE＝CE，
∵∠APB＝60°，
∴∠APB+∠AEC＝120°，
∴点A、P、C、E四点共圆，
∴∠APE＝∠EPC＝30°，
∴∠PEC＝∠PCE＝75°，
∴PE＝PC，
设PB＝a，则PA＝2a，AB＝BC＝，
∴PA+PC＝2a+a+＝（）＝（BC+PB）＝PC，
∴PA+PC＝PE．



考点四 正方形的性质与判定

11．在正方形ABCD中，E为AD上一点，连接BE．
（1）如图1，连接BD，延长BE至点F，使BF＝BD，且AF∥BD，
①若AB＝，求AF的长度；
②如图2，过点D作BF的垂线DG，垂足为点G，交AF于点H，分别延长BA，DH交于点P，连接PE，过点F作FQ⊥BD于Q．求证：BE＝DG+FG；
（2）如图3，延长DC至点R，使CR＝AE，在四边形BCDE内有点M，∠BME＝135°，点N为平面上一点，连接ND，MN，若AB＝5，AE＝1，请直接写出MN+ND+NR的最小值．

【解答】解：（1）①过点F作FG⊥AB，与BA的延长线交于点G，如图1，

∵四边形ABCD为正方形，AB＝，
∴∠DAG＝∠BAD＝∠ADC＝∠ABC＝90°，BD平分∠ADC和∠ABC，AB＝AD＝，
∴∠ADB＝45°，BD＝，
∵AF∥BD，
∴∠DAF＝∠ADB＝45°，
∴∠GAF＝45°，
∴∠AGF＝∠GAF＝45°，
∴AG＝GF，
不妨设AG＝GF＝x，则BG＝x+，
∵BG2+GF2＝BF2，BF＝BD＝2，
∴，
解得，x＝，或x＝﹣（舍），
∴AF＝AG＝﹣1；
②连接PF和DF，如图2，

∵DG⊥BF，
∴∠DGE＝∠BAE＝90°，
∵∠AEB＝∠DEG，
∴∠ABE＝∠GDE，
∵∠BAE＝∠DAP＝90°，AB＝AD，
∴△ABE≌△ADP（ASA），
∴BE＝DP，AE＝AP，
设AB＝a，则BF＝BE＝a，
∵AF∥BD，
∴S△FBD＝S△ABD，
∴，
∴FQ＝，
∴sin∠QBF＝，
∴∠QBF＝30°，
∵AF∥BD，
∴∠AFB＝∠DBF＝30°，∠EAF＝∠ADB＝45°，
∴∠EAF＝∠PAF＝45°，
∵AF＝AF，
∴△AEF≌△APF（SAS），
∴∠AFE＝∠AFP＝30°，
∴∠EFP＝60°，
∴PG＝，
∵DG+PG＝DP＝BE，
∴BE＝DG+FG；
（2）将△DNR绕点R顺时针旋转90°得△RPQ，作△BME的外接圆⊙O，连接OM、NP、PQ，连接OQ与⊙O交于M'，连接QR，延长AB与QR的延长线交于点K，过O作OL⊥QR于点L，作OF⊥AB于F，作OG⊥BE于点G，与AB交于点H，连接OA，OB，如图3，则QR＝DR，RK＝BC，KL＝OF，CR＝BK，OL＝FK，

∵OE＝OM＝OB，
∴∠OEM＝∠OME，∠OBM＝∠OMB，
∵∠BME＝135°，
∴∠OEM+∠OBM＝∠OME+∠OMB＝135°，
∴∠BOE＝90°，
∵四边形ABCD是正方形，AB＝5，
∴AB＝BC＝CD＝AD＝RK＝6，
∵AE＝CR＝1，
∴QR＝DR＝5+1＝6，BK＝1，
∴BE＝，
∴OG＝BG＝BE＝，OA＝OB＝OM'＝BE＝，
∵∠BGH＝∠BAE＝90°，∠HBG＝∠EBA，
∴△BGH∽△BAE，
∴＝，即＝，
∴GH＝，BH＝，
∴OH＝OG﹣GH＝，
∵∠OFH＝∠BGH＝90°，∠OHF＝∠BHG，
∴△OHF∽△BHG，
∴，即，
∴HF＝，OF＝2，
∴KL＝OF＝2，OL＝FK＝FH+BH+BK＝4，
∴QL＝QR+RK+KL＝13，
∴OQ＝＝＝，
由旋转知，∠PRN＝90°，PR＝RN，PQ＝DN，
∴PN＝，
∵OM+MN+ND+NR＝OM+MN+PN+PQ≥OQ，
∴当O、M、N、P、Q五点共线时，OM+MN+ND+NR＝OQ＝的值最小，
∵OM＝OB＝，
∴MN+ND+NR的最小值为：﹣．
12．如图，在正方形ABCD中，E，F分别是边BC，AB上一动点，且AF＝BE，连接DF，AE交于点G，连接CG．
（1）如图1，若CG＝AD，求证：CE＝AD；
（2）如图2，当点E，F分别在边BC，AB上运动时，在以GC为斜边构造等腰直角△CGH，连接DH，猜想∠HDG的大小是否为定值，并证明你的结论；
（3）如图3，在（2）的条件下，连接BH，当BH取得最小值时，请直接写出的值．

【解答】（1）延长DC、AE相交于点K，如图：

∵四边形ABCD是正方形，
∴AD＝BA，∠DAF＝90°＝∠ABE，
∵AF＝BE，
∴△ADF≌△BAE（SAS），
∴∠ADF＝∠BAE，
∴∠AFG+∠BAE＝∠AFG+∠ADF＝90°，
∴DF⊥AE，
∴∠K+∠CDG＝90°＝∠DGK＝∠CGD+∠CGK，
∵CG＝CD，
∴∠CDG＝∠CGD，
∴∠K＝∠CGK，
∴CK＝CG＝CD＝AB，
又∠CEK＝∠AEB，∠ECK＝∠EBA＝90°，
∴△CEK≌△BAE（AAS），
∴CE＝BE＝BC＝AD；
（2）∠HDG＝45°；证明如下：
连接AC，如图：

∵四边形ABCD是正方形，
∴CA＝CD，∠ACD＝45°，
∵等腰直角△HGC，
∴CG＝CH，∠GCH＝45°，
∴＝＝，∠ACG＝∠DCH，
∴△ACG∽△DCH，
∴∠CHD＝∠CGA＝∠CGH+∠AGD+∠DGH＝135°+∠DGH，
∴∠DHG＝360°﹣∠CHG﹣∠CHD
＝360°﹣90°﹣（135°+∠DGH）
＝135°﹣∠DGH，
∵∠DHG＝180°﹣∠HDG﹣∠DGH，
∴135°﹣∠DGH＝180°﹣∠HDG﹣∠DGH，
∴∠HDG＝45°；
（3）过点C作CN⊥DF于点N，取CD的中点M，以DM为斜边在正方形外作等腰Rt△DOM，过点O作OT⊥BC，交BC的延长线于点T，过点H作HL⊥BC于点L，过点O作OS⊥CD于点S，连接OH、MN、OB，

∵∠CDN+∠ADG＝90°＝∠DAG+∠ADG，
∴∠CDN＝∠DAG，
∵∠CND＝90°＝∠DGA，CD＝DA，
∴△CDN≌△DAG（AAS），
∴DN＝AG，
由（2）可知：∠GDH＝45°，AG＝DH，
∴DN＝DH，∠GDH＝45°＝∠MDO，
∴∠NDM＝∠HDO，
∵DM＝DO，
∴＝＝，
∴△DMN∽△DOH，
∴＝，
∵MN是Rt△CDN斜边上的中线，
∴DM＝MN，
∴OH＝DO＝DM＝CD，
∵TC＝OS＝DM＝CD，
∴OT＝CS＝CD，BT＝CD，
∴OB＝＝CD，
∴BH≥OB﹣OH＝CD，
故当BH取得最小值时，B、H、O共线，
此时由HL∥OT，可得：
＝＝，
即：＝，
∴＝，
∴＝＝•＝．