专题5.1 平面向量的概念及线性运算-2022年高考数学（理）一轮复习-题型全归纳与高效训练突破学案

这是一份专题5.1 平面向量的概念及线性运算-2022年高考数学（理）一轮复习-题型全归纳与高效训练突破学案，文件包含专题51平面向量的概念及线性运算解析版docx、专题51平面向量的概念及线性运算原卷版docx等2份学案配套教学资源，其中学案共33页， 欢迎下载使用。

目录
TOC \ "1-3" \h \u 一、题型全归纳1
题型一 平面向量的基本概念1
题型二 平面向量的线性运算3
题型三 平面向量共线定理的应用6
命题角度1 证明向量共线或三点共线6
命题角度2 由向量共线求参数的值7
命题角度3 证明三点共线7
题型四 共线定理的推广与应用8
二、高效训练突破10
一、题型全归纳
题型一 平面向量的基本概念
【题型要点】1．向量的有关概念
(1)向量：既有大小又有方向的量叫做向量，向量的大小叫做向量的模．
(2)零向量：长度为0的向量，其方向是任意的．
(3)单位向量：长度等于1个单位的向量．
(4)平行向量：方向相同或相反的非零向量，又叫共线向量，规定：0与任一向量共线．
(5)相等向量：长度相等且方向相同的向量．
(6)相反向量：长度相等且方向相反的向量．
2.五个特殊向量
(1)要注意0与0的区别，0是一个实数，0是一个向量，且|0|＝0.
(2)单位向量有无数个，它们大小相等，但方向不一定相同．
(3)任一组平行向量都可以平移到同一直线上，因此平行向量也叫做共线向量．
(4)与向量a平行的单位向量有两个，即向量eq \f(a,|a|)和－eq \f(a,|a|).
3.辨析向量有关概念的五个关键点
(1)向量定义的关键是方向和长度．
(2)非零共线向量的关键是方向相同或相反，长度没有限制．
(3)相等向量的关键是方向相同且长度相等．
(4)单位向量的关键是方向没有限制，但长度都是一个单位长度．
(5)零向量的关键是方向没有限制，长度是0，规定零向量与任何向量共线．
【例1】下列叙述错误的是________(填序号)．
①已知向量a∥b，且|a|>|b|>0，则向量a＋b的方向与向量a的方向相同；
②|a|＋|b|＝|a＋b|⇔a与b方向相同；
③向量b与向量a共线的充要条件是有且只有一个实数λ，使得b＝λa；
④eq \(AB,\s\up6(→))＋eq \(BA,\s\up6(→))＝0；
⑤若λa＝λb，则a＝b.
【答案】②③④⑤
【解析】对于①，当a和b方向相同，则它们的和的方向应该与a(或b)的方向相同；当a和b方向相反，而a的模大于b的模，则它们的和的方向与a的方向相同．
对于②，当a，b之一为零向量时结论不成立．
对于③，当a＝0且b＝0时，λ有无数个值；当a＝0但b≠0时，λ不存在．
对于④，由于两个向量之和仍是一个向量，所以eq \(AB,\s\up6(→))＋eq \(BA,\s\up6(→))＝0.
对于⑤，当λ＝0时，无论a与b的大小与方向如何，都有λa＝λb，此时不一定有a＝b.
故②③④⑤均错误．
【例2】下列命题中，正确的个数是( )
①若两个向量相等，则它们的起点和终点分别重合；
②若|a|＝|b|，则a＝b或a＝－b；
③若λa＝0(λ为实数)，则λ必为零；
④已知λ，μ为实数，若λa＝μb，则a与b共线．
A．0 B．1
C．2 D．3
【答案】A
【解析】①错误，如在▱ABCD中，eq \(AD,\s\up6(→))＝eq \(BC,\s\up6(→))，但是这两个向量的起点和终点分别不重合；②错误，模相等的两个向量，方向关系不确定；③错误，若λa＝0(λ为实数)，则λ＝0或a＝0；④错误，当λ＝μ＝0时，λa＝μb＝0，但a与b不一定共线．
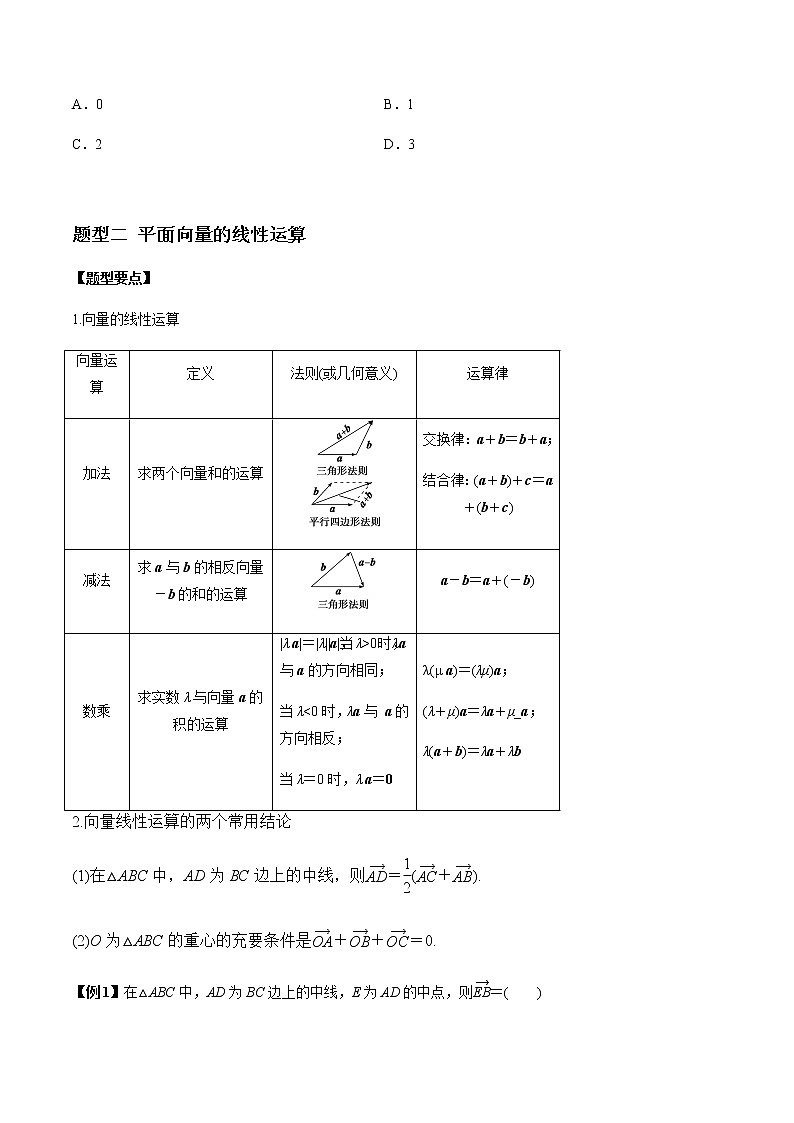
题型二 平面向量的线性运算
【题型要点】
1.向量的线性运算
2.向量线性运算的两个常用结论
(1)在△ABC中，AD为BC边上的中线，则eq \(AD,\s\up6(→))＝eq \f(1,2)(eq \(AC,\s\up6(→))＋eq \(AB,\s\up6(→))).
(2)O为△ABC的重心的充要条件是eq \(OA,\s\up6(→))＋eq \(OB,\s\up6(→))＋eq \(OC,\s\up6(→))＝0.
【例1】在△ABC中，AD为BC边上的中线，E为AD的中点，则eq \(EB,\s\up6(→))＝( )
A.eq \f(3,4)eq \(AB,\s\up6(→))－eq \f(1,4)eq \(AC,\s\up6(→)) B．eq \f(1,4)eq \(AB,\s\up6(→))－eq \f(3,4)eq \(AC,\s\up6(→))
C.eq \f(3,4)eq \(AB,\s\up6(→))＋eq \f(1,4)eq \(AC,\s\up6(→)) D．eq \f(1,4)eq \(AB,\s\up6(→))＋eq \f(3,4)eq \(AC,\s\up6(→))
【答案】A
【解析】
法一：如图所示，eq \(EB,\s\up6(→))＝eq \(ED,\s\up6(→))＋eq \(DB,\s\up6(→))＝eq \f(1,2)eq \(AD,\s\up6(→))＋eq \f(1,2)eq \(CB,\s\up6(→))＝eq \f(1,2)×eq \f(1,2)(eq \(AB,\s\up6(→))＋eq \(AC,\s\up6(→)))＋eq \f(1,2)(eq \(AB,\s\up6(→))－eq \(AC,\s\up6(→)))＝eq \f(3,4)eq \(AB,\s\up6(→))－eq \f(1,4)eq \(AC,\s\up6(→))，故选A.
法二：eq \(EB,\s\up6(→))＝eq \(AB,\s\up6(→))－eq \(AE,\s\up6(→))＝eq \(AB,\s\up6(→))－eq \f(1,2)eq \(AD,\s\up6(→))＝eq \(AB,\s\up6(→))－eq \f(1,2)×eq \f(1,2)(eq \(AB,\s\up6(→))＋eq \(AC,\s\up6(→)))＝eq \f(3,4)eq \(AB,\s\up6(→))－eq \f(1,4)eq \(AC,\s\up6(→))，故选A.
【例2】(2020云南省楚雄州十校联考)如图，在直角梯形ABCD中，eq \(DC,\s\up6(→))＝eq \f(1,4)eq \(AB,\s\up6(→))，eq \(BE,\s\up6(→))＝2eq \(EC,\s\up6(→))，且eq \(AE,\s\up6(→))＝req \(AB,\s\up6(→))＋seq \(AD,\s\up6(→))，则2r＋3s＝( )
A．1 B．2
C．3 D．4
【答案】C
【解析】 法一：由题图可得eq \(AE,\s\up6(→))＝eq \(AB,\s\up6(→))＋eq \(BE,\s\up6(→))＝eq \(AB,\s\up6(→))＋eq \f(2,3)eq \(BC,\s\up6(→))＝eq \(AB,\s\up6(→))＋eq \f(2,3)(eq \(BA,\s\up6(→))＋eq \(AD,\s\up6(→))＋eq \(DC,\s\up6(→)))＝eq \f(1,3)eq \(AB,\s\up6(→))＋eq \f(2,3)(eq \(AD,\s\up6(→))＋eq \(DC,\s\up6(→)))＝eq \f(1,3)eq \(AB,\s\up6(→))＋eq \f(2,3)(eq \(AD,\s\up6(→))＋eq \f(1,4)eq \(AB,\s\up6(→)))＝eq \f(1,2)eq \(AB,\s\up6(→))＋eq \f(2,3)eq \(AD,\s\up6(→)).因为eq \(AE,\s\up6(→))＝req \(AB,\s\up6(→))＋seq \(AD,\s\up6(→))，所以r＝eq \f(1,2)，s＝eq \f(2,3)，则2r＋3s＝1＋2＝3.
法二：因为eq \(BE,\s\up6(→))＝2eq \(EC,\s\up6(→))，所以eq \(AE,\s\up6(→))－eq \(AB,\s\up6(→))＝2(eq \(AC,\s\up6(→))－eq \(AE,\s\up6(→)))，整理，得eq \(AE,\s\up6(→))＝eq \f(1,3)eq \(AB,\s\up6(→))＋eq \f(2,3)eq \(AC,\s\up6(→))＝eq \f(1,3)eq \(AB,\s\up6(→))＋eq \f(2,3)(eq \(AD,\s\up6(→))＋eq \(DC,\s\up6(→)))＝eq \f(1,2)eq \(AB,\s\up6(→))＋eq \f(2,3)eq \(AD,\s\up6(→))，以下同法一．
法三：如图，延长AD，BC交于点P，则由eq \(DC,\s\up6(→))＝eq \f(1,4)eq \(AB,\s\up6(→))得DC∥AB，且AB＝4DC.
又eq \(BE,\s\up6(→))＝2eq \(EC,\s\up6(→))，所以E为PB的中点，且eq \(AP,\s\up6(→))＝eq \f(4,3)eq \(AD,\s\up6(→)).
于是，eq \(AE,\s\up6(→))＝eq \f(1,2)(eq \(AB,\s\up6(→))＋eq \(AP,\s\up6(→)))＝eq \f(1,2)eq \b\lc\(\rc\)(\a\vs4\al\c1(\(AB,\s\up6(→))＋\f(4,3)\(AD,\s\up6(→))))＝eq \f(1,2)eq \(AB,\s\up6(→))＋eq \f(2,3)eq \(AD,\s\up6(→)).以下同法一．
法四：如图，建立平面直角坐标系xAy，依题意可设点B(4m，0)，D(3m，3h)，E(4m，2h)，其中m＞0，h＞0.
由eq \(AE,\s\up6(→))＝req \(AB,\s\up6(→))＋seq \(AD,\s\up6(→))，得(4m，2h)＝r(4m，0)＋s(3m，3h)，
所以eq \b\lc\{(\a\vs4\al\c1(4m＝4mr＋3ms，,2h＝3hs，))解得eq \b\lc\{(\a\vs4\al\c1(r＝\f(1,2)，,s＝\f(2,3)，))
所以2r＋3s＝1＋2＝3.
题型三 平面向量共线定理的应用
【题型要点】求解向量共线问题的注意事项
(1)向量共线的充要条件中，当两向量共线时，通常只有非零向量才能表示与之共线的其他向量，注意待定系数法和方程思想的运用.
(2)证明三点共线问题，可用向量共线来解决，但应注意向量共线与三点共线的区别与联系，当两向量共线且有公共点时，才能得到三点共线．
(3)若a与b不共线且λa＝μb，则λ＝μ＝0.
(4)直线的向量式参数方程，A，P，B三点共线⇔eq \(OP,\s\up6(→))＝(1－t)eq \(OA,\s\up6(→))＋teq \(OB,\s\up6(→))(O为平面内任一点，t∈R)．
eq \(OA,\s\up6(→))＝λeq \(OB,\s\up6(→))＋μeq \(OC,\s\up6(→))(λ，μ为实数)，若A，B，C三点共线，则λ＋μ＝1.
命题角度1 证明向量共线或三点共线
【例1】已知平面内一点P及△ABC，若eq \(PA,\s\up6(→))＋eq \(PB,\s\up6(→))＋eq \(PC,\s\up6(→))＝eq \(AB,\s\up6(→))，则点P与△ABC的位置关系是( )
A．点P在线段AB上 B．点P在线段BC上
C．点P在线段AC上 D．点P在△ABC外部
【答案】C
【解析】因为eq \(PA,\s\up6(→))＋eq \(PB,\s\up6(→))＋eq \(PC,\s\up6(→))＝eq \(AB,\s\up6(→))＝eq \(PB,\s\up6(→))－eq \(PA,\s\up6(→))，所以eq \(PC,\s\up6(→))＝－2eq \(PA,\s\up6(→))，所以A，P，C三点共线，且P是线段AC的三等分点(靠近A)．
【升华】证明向量共线：对于向量a，b，若存在实数λ，使a＝λb(b≠0)，则a与b共线．
命题角度2 由向量共线求参数的值
【例2】(2020·安徽合肥一中高考模拟)如图，在平行四边形ABCD中，M，N分别为AB，AD上的点，且eq \(AM,\s\up6(→))＝eq \f(4,5)eq \(AB,\s\up6(→))，连接AC，MN交于点P，若eq \(AP,\s\up6(→))＝eq \f(4,11)eq \(AC,\s\up6(→))，则点N在AD上的位置为( )
A．AD中点
B．AD上靠近点D的三等分点
C．AD上靠近点D的四等分点
D．AD上靠近点D的五等分点
【答案】B
【解析】设eq \(AD,\s\up6(→))＝λeq \(AN,\s\up6(→))，因为eq \(AP,\s\up6(→))＝eq \f(4,11)eq \(AC,\s\up6(→))＝eq \f(4,11)(eq \(AB,\s\up6(→))＋eq \(AD,\s\up6(→)))＝eq \f(4,11)eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(5,4)\(AM,\s\up6(→))＋λ\(AN,\s\up6(→))))＝eq \f(5,11)eq \(AM,\s\up6(→))＋eq \f(4λ,11)eq \(AN,\s\up6(→))，又M，N，P三点共线，所以eq \f(5,11)＋eq \f(4λ,11)＝1，解得λ＝eq \f(3,2)，所以eq \(AN,\s\up6(→))＝eq \f(2,3)eq \(AD,\s\up6(→))，所以点N在AD上靠近点D的三等分点．
【升华】求参数的值：利用共线向量定理及向量相等的条件列方程(组)求参数的值．
命题角度3 证明三点共线
【例3】(2020·江西吉安一中、新余一中等八所中学联考)设两个非零向量a与b不共线．
(1)若eq \(AB,\s\up6(→))＝a＋b，eq \(BC,\s\up6(→))＝2a＋8b，eq \(CD,\s\up6(→))＝3(a－b)，求证：A，B，D三点共线；
(2)试确定实数k，使ka＋b和a＋kb共线．
【答案】见解析
【解析】 (1)证明：因为eq \(AB,\s\up6(→))＝a＋b，eq \(BC,\s\up6(→))＝2a＋8b，eq \(CD,\s\up6(→))＝3(a－b)，所以eq \(BD,\s\up6(→))＝eq \(BC,\s\up6(→))＋eq \(CD,\s\up6(→))＝2a＋8b＋3(a－b)＝5(a＋b)＝5eq \(AB,\s\up6(→))，
所以eq \(AB,\s\up6(→))，eq \(BD,\s\up6(→))共线，又它们有公共点B，
所以A，B，D三点共线．
(2)因为ka＋b与a＋kb共线，
所以存在实数λ，使ka＋b＝λ(a＋kb)，
即(k－λ)a＝(λk－1)b.
又a，b是两个不共线的非零向量，
所以k－λ＝λk－1＝0.所以k2－1＝0.
所以k＝±1.
【规律】证明三点共线：若存在实数λ，使eq \(AB,\s\up6(→))＝λeq \(AC,\s\up6(→))，则A，B，C三点共线．
题型四 共线定理的推广与应用
【题型要点】
一、共线定理：已知eq \(PA,\s\up6(→))，eq \(PB,\s\up6(→))为平面内两个不共线的向量，设eq \(PC,\s\up6(→))＝xeq \(PA,\s\up6(→))＋yeq \(PB,\s\up6(→))，则A，B，C三点共线的充要条件为x＋y＝1.
二、推广形式：如图所示，直线DE∥AB，C为直线DE上任一点，设eq \(PC,\s\up6(→))＝xeq \(PA,\s\up6(→))＋yeq \(PB,\s\up6(→))(x，y∈R)．
当直线DE不过点P时，直线PC与直线AB的交点记为F，因为点F在直线AB上，所以由三点共线结论可知，若eq \(PF,\s\up6(→))＝λeq \(PA,\s\up6(→))＋μeq \(PB,\s\up6(→))(λ，μ∈R)，则λ＋μ＝1.由△PAB与△PED相似，知必存在一个常数m∈R，使得eq \(PC,\s\up6(→))＝m eq \(PF,\s\up6(→))，则eq \(PC,\s\up6(→))＝meq \(PF,\s\up6(→))＝mλeq \(PA,\s\up6(→))＋mμeq \(PB,\s\up6(→)).
又eq \(PC,\s\up6(→))＝xeq \(PA,\s\up6(→))＋yeq \(PB,\s\up6(→))(x，y∈R)，
所以x＋y＝mλ＋mμ＝m.
以上过程可逆．
因此得到结论：eq \(PC,\s\up6(→))＝xeq \(PA,\s\up6(→))＋yeq \(PB,\s\up6(→))，
则x＋y＝m(定值)，反之亦成立．
【例1】(2020·江西上饶重点中学六校联考)如图所示，A，B，C是圆O上的三点，线段CO的延长线与BA的延长线交于圆O外一点D，若eq \(OC,\s\up6(→))＝meq \(OA,\s\up6(→))＋neq \(OB,\s\up6(→))，则m＋n的取值范围是________．
【答案】 (－1，0)
【解析】 由点D是圆O外的一点，可设eq \(BD,\s\up6(→))＝λeq \(BA,\s\up6(→))(λ＞1)，则eq \(OD,\s\up6(→))＝eq \(OB,\s\up6(→))＋eq \(BD,\s\up6(→))＝eq \(OB,\s\up6(→))＋λeq \(BA,\s\up6(→))＝λeq \(OA,\s\up6(→))＋(1－λ)eq \(OB,\s\up6(→)).因为C，O，D三点共线，令eq \(OD,\s\up6(→))＝－μeq \(OC,\s\up6(→))(μ＞1)，所以eq \(OC,\s\up6(→))＝－eq \f(λ,μ)eq \(OA,\s\up6(→))－eq \f(1－λ,μ)·eq \(OB,\s\up6(→))(λ＞1，μ＞1)．因为eq \(OC,\s\up6(→))＝meq \(OA,\s\up6(→))＋neq \(OB,\s\up6(→))，所以m＝－eq \f(λ,μ)，n＝－eq \f(1－λ,μ)，则m＋n＝－eq \f(λ,μ)－eq \f(1－λ,μ)＝－eq \f(1,μ)∈(－1，0)．
【例2】 如图，在扇形OAB中，∠AOB＝eq \f(π,3)，C为弧AB上的动点，若eq \(OC,\s\up6(→))＝xeq \(OA,\s\up6(→))＋yeq \(OB,\s\up6(→))，则x＋3y的取值范围是________．
【答案】 [1，3]
【解析】 eq \(OC,\s\up6(→))＝xeq \(OA,\s\up6(→))＋3yeq \b\lc\(\rc\)(\a\vs4\al\c1(\f(\(OB,\s\up6(→)),3)))，如图，作eq \(OB′,\s\up6(→))＝eq \f(\(OB,\s\up6(→)),3)，则考虑以向量eq \(OA,\s\up6(→))，eq \(OB′,\s\up6(→))为基底．显然，当C在A点时，经过m＝1的平行线，当C在B点时，经过m＝3的平行线，这两条
线分别是最近与最远的平行线，所以x＋3y的取值范围是[1，3]．
二、高效训练突破
一、选择题
1．设a0为单位向量，①若a为平面内的某个向量，则a＝|a|a0；②若a与a0平行，则a＝|a|a0；③若a与a0平行且|a|＝1，则a＝a0.上述命题中，假命题的个数是( )
A．0 B．1
C．2 D．3
【答案】D.
【解析】：向量是既有大小又有方向的量，a与|a|a0的模相同，但方向不一定相同，故①是假命题；若a与a0平行，则a与a0的方向有两种情况：一是同向，二是反向，反向时a＝－|a|a0，故②③也是假命题．综上所述，假命题的个数是3.
2．设a，b都是非零向量，下列四个条件中，使eq \f(a,|a|)＝eq \f(b,|b|)成立的充分条件是( )
A．a＝－b B．a∥b
C．a＝2b D．a∥b且|a|＝|b|
【答案】C.
【解析】：因为向量eq \f(a,|a|)的方向与向量a相同，向量eq \f(b,|b|)的方向与向量b相同，且eq \f(a,|a|)＝eq \f(b,|b|)，所以向量a与向量b方向相同，故可排除选项A，B，D.当a＝2b时，eq \f(a,|a|)＝eq \f(2b,|2b|)＝eq \f(b,|b|)，故“a＝2b”是“eq \f(a,|a|)＝eq \f(b,|b|)”成立的充分条件．
3.已知向量a，b不共线，且c＝λa＋b，d＝a＋(2λ－1)b，若c与d反向共线，则实数λ的值为( )
A．1 B．－eq \f(1,2)
C．1或－eq \f(1,2) D．－1或－eq \f(1,2)
【答案】B
【解析】由于c与d反向共线，则存在实数k使c＝kd(k<0)，于是λa＋b＝k[a＋(2λ－1)b]．整理得λa＋b＝ka＋(2λk－k)b.由于a，b不共线，所以有eq \b\lc\{\rc\ (\a\vs4\al\c1(λ＝k，,2λk－k＝1，))整理得2λ2－λ－1＝0，解得λ＝1或λ＝－eq \f(1,2).又k<0，所以λ<0，故λ＝－eq \f(1,2).
4．已知点O，A，B不在同一条直线上，点P为该平面上一点，且2eq \(OP,\s\up6(→))＝2eq \(OA,\s\up6(→))＋eq \(BA,\s\up6(→))，则( )
A．点P在线段AB上
B．点P在线段AB的反向延长线上
C．点P在线段AB的延长线上
D．点P不在直线AB上
【答案】B
【解析】因为2eq \(OP,\s\up6(→))＝2eq \(OA,\s\up6(→))＋eq \(BA,\s\up6(→))，所以2eq \(AP,\s\up6(→))＝eq \(BA,\s\up6(→))，所以点P在线段AB的反向延长线上，故选B.
5.如图，已知eq \(AP,\s\up6(→))＝eq \f(4,3)eq \(AB,\s\up6(→))，用eq \(OA,\s\up6(→))，eq \(OB,\s\up6(→))表示eq \(OP,\s\up6(→))，则eq \(OP,\s\up6(→))等于( )
A.eq \f(1,3)eq \(OA,\s\up6(→))－eq \f(4,3)eq \(OB,\s\up6(→)) B.eq \f(1,3)eq \(OA,\s\up6(→))＋eq \f(4,3)eq \(OB,\s\up6(→))
C．－eq \f(1,3)eq \(OA,\s\up6(→))＋eq \f(4,3)eq \(OB,\s\up6(→)) D．－eq \f(1,3)eq \(OA,\s\up6(→))－eq \f(4,3)eq \(OB,\s\up6(→))
【答案】C.
【解析】：eq \(OP,\s\up6(→))＝eq \(OA,\s\up6(→))＋eq \(AP,\s\up6(→))＝eq \(OA,\s\up6(→))＋eq \f(4,3)eq \(AB,\s\up6(→))＝eq \(OA,\s\up6(→))＋eq \f(4,3)(eq \(OB,\s\up6(→))－eq \(OA,\s\up6(→)))＝－eq \f(1,3)eq \(OA,\s\up6(→))＋eq \f(4,3)eq \(OB,\s\up6(→)).故选C.
6．在△ABC中，AB＝2，BC＝3，∠ABC＝60°，AD为BC边上的高，O为AD的中点，若eq \(AO,\s\up6(→))＝λeq \(AB,\s\up6(→))＋μeq \(BC,\s\up6(→))，其中λ，μ∈R，则λ＋μ等于( )
A．1 B．eq \f(1,2)
C.eq \f(1,3) D．eq \f(2,3)
【答案】D.
【解析】：由题意易得eq \(AD,\s\up6(→))＝eq \(AB,\s\up6(→))＋eq \(BD,\s\up6(→))＝eq \(AB,\s\up6(→))＋eq \f(1,3)eq \(BC,\s\up6(→))，所以2eq \(AO,\s\up6(→))＝eq \(AB,\s\up6(→))＋eq \f(1,3)eq \(BC,\s\up6(→))，即eq \(AO,\s\up6(→))＝eq \f(1,2)eq \(AB,\s\up6(→))＋eq \f(1,6)eq \(BC,\s\up6(→)).
故λ＋μ＝eq \f(1,2)＋eq \f(1,6)＝eq \f(2,3).
7．(2020·广东华附、省实、广雅、深中联考)设a，b是非零向量，记a与b所成的角为θ，下列四个条件中，使eq \f(a,|a|)＝eq \f(b,|b|)成立的充要条件是( )
A．a∥b B．θ＝0
C．θ＝eq \f(π,2) D．θ＝π
【答案】B.
【解析】：eq \f(a,|a|)＝eq \f(b,|b|)等价于非零向量a与b同向共线，即θ＝0，故选B.
8．(2020·广东一模)已知A，B，C三点不共线，且点O满足16eq \(OA,\s\up6(→))－12eq \(OB,\s\up6(→))－3eq \(OC,\s\up6(→))＝0，则( )
A.eq \(OA,\s\up6(→))＝12eq \(AB,\s\up6(→))＋3eq \(AC,\s\up6(→)) B．eq \(OA,\s\up6(→))＝12eq \(AB,\s\up6(→))－3eq \(AC,\s\up6(→))
C.eq \(OA,\s\up6(→))＝－12eq \(AB,\s\up6(→))＋3eq \(AC,\s\up6(→)) D．eq \(OA,\s\up6(→))＝－12eq \(AB,\s\up6(→))－3eq \(AC,\s\up6(→))
【答案】A.
【解析】：对于A，eq \(OA,\s\up6(→))＝12eq \(AB,\s\up6(→))＋3eq \(AC,\s\up6(→))＝12(eq \(OB,\s\up6(→))－eq \(OA,\s\up6(→)))＋3(eq \(OC,\s\up6(→))－eq \(OA,\s\up6(→)))＝12eq \(OB,\s\up6(→))＋3eq \(OC,\s\up6(→))－15eq \(OA,\s\up6(→))，整理，可得16eq \(OA,\s\up6(→))－12eq \(OB,\s\up6(→))－3eq \(OC,\s\up6(→))＝0，这与题干中条件相符合，故选A.
9.已知向量a，b不共线，且c＝λa＋b，d＝a＋(2λ－1)b，若c与d反向共线，则实数λ的值为( )
A．1 B．－eq \f(1,2)
C．1或－eq \f(1,2) D．－1或－eq \f(1,2)
【答案】B.
【解析】：由于c与d反向共线，则存在实数k使c＝kd(k＜0)，于是λa＋b＝k[a＋(2λ－1)b]．整理得λa＋b＝ka＋(2λk－k)b.由于a，b不共线，所以有eq \b\lc\{(\a\vs4\al\c1(λ＝k，,2λk－k＝1，))整理得2λ2－λ－1＝0，解得λ＝1或λ＝－eq \f(1,2).又因为k＜0，所以λ＜0，故λ＝－eq \f(1,2).
10.(2020·福州模拟)庄严美丽的国旗和国徽上的五角星是革命和光明的象征．正五角星是一个非常优美的几何图形，且与黄金分割有着密切的联系．在如图所示的正五角星中，以A，B，C，D，E为顶点的多边形为正五边形，且eq \f(PT,AT)＝eq \f(\r(5)－1,2).则下列关系中正确的是( )
A.eq \(BP,\s\up6(→))－eq \(TS,\s\up6(→))＝eq \f(\r(5)＋1,2)eq \(RS,\s\up6(→)) B．eq \(CQ,\s\up6(→))＋eq \(TP,\s\up6(→))＝eq \f(\r(5)＋1,2)eq \(TS,\s\up6(→))
C.eq \(ES,\s\up6(→))－eq \(AP,\s\up6(→))＝eq \f(\r(5)－1,2)eq \(BQ,\s\up6(→)) D．eq \(AT,\s\up6(→))＋eq \(BQ,\s\up6(→))＝eq \f(\r(5)－1,2)eq \(CR,\s\up6(→))
【答案】A.
【解析】：由题意得，eq \(BP,\s\up6(→))－eq \(TS,\s\up6(→))＝eq \(TE,\s\up6(→))－eq \(TS,\s\up6(→))＝eq \(SE,\s\up6(→))＝eq \f(\(RS,\s\up6(→)),\f(\r(5)－1,2))＝eq \f(\r(5)＋1,2)eq \(RS,\s\up6(→))，所以A正确；eq \(CQ,\s\up6(→))＋eq \(TP,\s\up6(→))＝eq \(PA,\s\up6(→))＋eq \(TP,\s\up6(→))＝eq \(TA,\s\up6(→))＝eq \f(\r(5)＋1,2)eq \(ST,\s\up6(→))，所以B错误；eq \(ES,\s\up6(→))－eq \(AP,\s\up6(→))＝eq \(RC,\s\up6(→))－eq \(QC,\s\up6(→))＝eq \(RQ,\s\up6(→))＝eq \f(\r(5)－1,2)eq \(QB,\s\up6(→))，所以C错误；eq \(AT,\s\up6(→))＋eq \(BQ,\s\up6(→))＝eq \(SD,\s\up6(→))＋eq \(RD,\s\up6(→))，eq \f(\r(5)－1,2)eq \(CR,\s\up6(→))＝eq \(RS,\s\up6(→))＝eq \(RD,\s\up6(→))－eq \(SD,\s\up6(→))，若eq \(AT,\s\up6(→))＋eq \(BQ,\s\up6(→))＝eq \f(\r(5)－1,2)eq \(CR,\s\up6(→))，则eq \(SD,\s\up6(→))＝0，不合题意，所以D错误．故选A.
11.如图，在△ABC中，点D在线段BC上，且满足BD＝eq \f(1,2)DC，过点D的直线分别交直线AB，AC于不同的两点M，N若eq \(AM,\s\up6(→))＝meq \(AB,\s\up6(→))，eq \(AN,\s\up6(→))＝neq \(AC,\s\up6(→))，则( )
A．m＋n是定值，定值为2 B．2m＋n是定值，定值为3
C.eq \f(1,m)＋eq \f(1,n)是定值，定值为2 D.eq \f(2,m)＋eq \f(1,n)是定值，定值为3
【答案】D.
【解析】：法一：如图，过点C作CE平行于MN交AB于点E.由eq \(AN,\s\up6(→))＝neq \(AC,\s\up6(→))可得eq \f(AC,AN)＝eq \f(1,n)，所以eq \f(AE,EM)＝eq \f(AC,CN)＝eq \f(1,n－1)，由BD＝eq \f(1,2)DC可得eq \f(BM,ME)＝eq \f(1,2)，所以eq \f(AM,AB)＝eq \f(n,n＋\f(n－1,2))＝eq \f(2n,3n－1)，因为eq \(AM,\s\up6(→))＝meq \(AB,\s\up6(→))，所以m＝eq \f(2n,3n－1)，
整理可得eq \f(2,m)＋eq \f(1,n)＝3.
法二：因为M，D，N三点共线，所以eq \(AD,\s\up6(→))＝λeq \(AM,\s\up6(→))＋(1－λ)·eq \(AN,\s\up6(→)).
又eq \(AM,\s\up6(→))＝meq \(AB,\s\up6(→))，eq \(AN,\s\up6(→))＝neq \(AC,\s\up6(→))，所以eq \(AD,\s\up6(→))＝λmeq \(AB,\s\up6(→))＋(1－λ)·neq \(AC,\s\up6(→)).又eq \(BD,\s\up6(→))＝eq \f(1,2)eq \(DC,\s\up6(→))，所以eq \(AD,\s\up6(→))－eq \(AB,\s\up6(→))＝eq \f(1,2)eq \(AC,\s\up6(→))－eq \f(1,2)eq \(AD,\s\up6(→))，所以eq \(AD,\s\up6(→))＝eq \f(1,3)eq \(AC,\s\up6(→))＋eq \f(2,3)eq \(AB,\s\up6(→)).比较系数知λm＝eq \f(2,3)，(1－λ)n＝eq \f(1,3)，所以eq \f(2,m)＋eq \f(1,n)＝3，故选D.
12.点O是△ABC内一点，满足条件eq \(OA,\s\up6(→))＝2eq \(BO,\s\up6(→))＋3eq \(CO,\s\up6(→))，延长BO交AC于点D，则eq \f(S△COD,S△AOD)的值为( )
A.eq \f(2,3) B.eq \f(1,3)
C.eq \f(1,2) D.eq \f(3,4)
【答案】B
【解析】解法一：如图(1)，分别取BC，AC的中点为E，F，连接EF.∵eq \(OA,\s\up6(→))＝2eq \(BO,\s\up6(→))＋3eq \(CO,\s\up6(→))，∴eq \(OA,\s\up6(→))－eq \(CO,\s\up6(→))＝2(eq \(BO,\s\up6(→))＋eq \(CO,\s\up6(→)))，即eq \(OA,\s\up6(→))＋eq \(OC,\s\up6(→))＝－2(eq \(OB,\s\up6(→))＋eq \(OC,\s\up6(→)))，∴2eq \(OF,\s\up6(→))＝－2·2eq \(OE,\s\up6(→))，∴eq \(OF,\s\up6(→))＝－2eq \(OE,\s\up6(→)).故O在△ABC的中位线EF上，且OF＝2OE.过点E作EH∥CD，交BD于点H，则H为BD的中点，EH＝eq \f(1,2)CD＝eq \f(1,2)DF，因此CD＝DF，CD∶AD＝1∶3，∴eq \f(S△COD,S△AOD)＝eq \f(CD,AD)＝eq \f(1,3).故选B.
解法二：∵eq \(OA,\s\up6(→))＋2eq \(OB,\s\up6(→))＋3eq \(OC,\s\up6(→))＝0，令2eq \(OB,\s\up6(→))＝eq \(OB′,\s\up6(→))，3eq \(OC,\s\up6(→))＝eq \(OC′,\s\up6(→))，∴eq \(OA,\s\up6(→))＋eq \(OB′,\s\up6(→))＋eq \(OC′,\s\up6(→))＝0，∴O是△AB′C′的重心，如图(2)，延长B′O交AC′于点F，则AF＝FC′.过点C作CE∥AC′，交BF于点E，∴eq \f(CD,AD)＝eq \f(CE,AF)＝eq \f(CE,C′F)＝eq \f(OC,OC′)＝eq \f(1,3)，∴eq \f(S△COD,S△AOD)＝eq \f(CD,AD)＝eq \f(1,3).故选B.
二、填空题
1.(2020·河南三市联考)若eq \(AP,\s\up6(→))＝eq \f(1,2)eq \(PB,\s\up6(→))，eq \(AB,\s\up6(→))＝(λ＋1)eq \(BP,\s\up6(→))，则λ＝________.
【答案】－eq \f(5,2)
【解析】∵eq \(AP,\s\up6(→))＝eq \f(1,2)eq \(PB,\s\up6(→))，∴eq \(AP,\s\up6(→))＋eq \(PB,\s\up6(→))＝eq \(AB,\s\up6(→))＝eq \f(3,2)eq \(PB,\s\up6(→))＝－eq \f(3,2)eq \(BP,\s\up6(→)).∴λ＋1＝－eq \f(3,2)，λ＝－eq \f(5,2).
2.在△ABC中，点D在线段BC的延长线上，且eq \(BC,\s\up6(→))＝3eq \(CD,\s\up6(→))，点O在线段CD上(与点C，D不重合)，若eq \(AO,\s\up6(→))＝xeq \(AB,\s\up6(→))＋(1－x)eq \(AC,\s\up6(→))，则x的取值范围是________．
【答案】：
【解析】：设eq \(CO,\s\up6(→))＝yeq \(BC,\s\up6(→))，因为eq \(AO,\s\up6(→))＝eq \(AC,\s\up6(→))＋eq \(CO,\s\up6(→))＝eq \(AC,\s\up6(→))＋yeq \(BC,\s\up6(→))＝eq \(AC,\s\up6(→))＋y(eq \(AC,\s\up6(→))－eq \(AB,\s\up6(→)))＝－yeq \(AB,\s\up6(→))＋(1＋y)eq \(AC,\s\up6(→)).
因为eq \(BC,\s\up6(→))＝3eq \(CD,\s\up6(→))，点O在线段CD上(与点C，D不重合)．
所以y∈，
因为eq \(AO,\s\up6(→))＝xeq \(AB,\s\up6(→))＋(1－x)eq \(AC,\s\up6(→))，
所以x＝－y，所以x∈
2.设两个非零向量a与b不共线，若a与b的起点相同，且a，tb，eq \f(1,3)(a＋b)的终点在同一条直线上，则实数t＝________．
【答案】：eq \f(1,2)
【解析】：因为a，tb，eq \f(1,3)(a＋b)三个向量的终点在同一条直线上，且a与b的起点相同，
所以a－tb与a－eq \f(1,3)(a＋b)共线，即a－tb与eq \f(2,3)a－eq \f(1,3)b共线，
所以存在实数λ，使a－tb＝λeq \b\lc\(\rc\)(\a\vs4\al\c1(\f(2,3)a－\f(1,3)b))，所以eq \b\lc\{(\a\vs4\al\c1(1＝\f(2,3)λ，,t＝\f(1,3)λ，))解得λ＝eq \f(3,2)，t＝eq \f(1,2).
3．如图，一直线EF与平行四边形ABCD的两边AB，AD分别交于E，F两点，且交对角线AC于点K，其中eq \(AE,\s\up6(→))＝eq \f(2,5)eq \(AB,\s\up6(→))，eq \(AF,\s\up6(→))＝eq \f(1,2)eq \(AD,\s\up6(→))，eq \(AK,\s\up6(→))＝λeq \(AC,\s\up6(→))，则λ＝________．
【答案】：eq \f(2,9)
【解析】：因为eq \(AE,\s\up6(→))＝eq \f(2,5)eq \(AB,\s\up6(→))，eq \(AF,\s\up6(→))＝eq \f(1,2)eq \(AD,\s\up6(→))，
所以eq \(AB,\s\up6(→))＝eq \f(5,2)eq \(AE,\s\up6(→))，eq \(AD,\s\up6(→))＝2eq \(AF,\s\up6(→)).
由向量加法的平行四边形法则可知，eq \(AC,\s\up6(→))＝eq \(AB,\s\up6(→))＋eq \(AD,\s\up6(→))，
所以eq \(AK,\s\up6(→))＝λeq \(AC,\s\up6(→))＝λ(eq \(AB,\s\up6(→))＋eq \(AD,\s\up6(→)))＝λeq \b\lc\(\rc\)(\a\vs4\al\c1(\f(5,2)\(AE,\s\up6(→))＋2\(AF,\s\up6(→))))＝eq \f(5,2)λeq \(AE,\s\up6(→))＋2λeq \(AF,\s\up6(→))，由E，F，K三点共线，可得λ＝eq \f(2,9).
4.(2020·青岛质检)已知D，E，F分别为△ABC的边BC，CA，AB的中点，且eq \(BC,\s\up6(→))＝a，eq \(CA,\s\up6(→))＝b，给出下列命题：
①eq \(AD,\s\up6(→))＝eq \f(1,2)a－b；②eq \(BE,\s\up6(→))＝a＋eq \f(1,2)b；③eq \(CF,\s\up6(→))＝－eq \f(1,2)a＋eq \f(1,2)b；④eq \(AD,\s\up6(→))＋eq \(BE,\s\up6(→))＋eq \(CF,\s\up6(→))＝0.
其中正确命题的序号为________．
【答案】 ②③④
【解析】 eq \(AD,\s\up6(→))＝eq \(CD,\s\up6(→))－eq \(CA,\s\up6(→))＝－eq \f(1,2)eq \(BC,\s\up6(→))－eq \(CA,\s\up6(→))＝－eq \f(1,2)a－b，所以①错误；eq \(BE,\s\up6(→))＝eq \(BC,\s\up6(→))＋eq \(CE,\s\up6(→))＝eq \(BC,\s\up6(→))＋eq \f(1,2)eq \(CA,\s\up6(→))＝a＋eq \f(1,2)b，故②正确；eq \(CF,\s\up6(→))＝eq \f(1,2)(eq \(CA,\s\up6(→))＋eq \(CB,\s\up6(→)))＝eq \f(1,2)(b－a)＝－eq \f(1,2)a＋eq \f(1,2)b，故③正确；综上知eq \(AD,\s\up6(→))＋eq \(BE,\s\up6(→))＋eq \(CF,\s\up6(→))＝eq \b\lc\(\rc\)(\a\vs4\al\c1(－\f(1,2)a－b))＋eq \b\lc\(\rc\)(\a\vs4\al\c1(a＋\f(1,2)b))＋eq \b\lc\(\rc\)(\a\vs4\al\c1(－\f(1,2)a＋\f(1,2)b))＝0，故④正确．
5.已知O为△ABC内一点，且2eq \(AO,\s\up6(→))＝eq \(OB,\s\up6(→))＋eq \(OC,\s\up6(→))，eq \(AD,\s\up6(→))＝teq \(AC,\s\up6(→))，若B，O，D三点共线，则t的值为________．
【答案】：eq \f(1,3)
【解析】：设线段BC的中点为M，则eq \(OB,\s\up6(→))＋eq \(OC,\s\up6(→))＝2eq \(OM,\s\up6(→)).
因为2eq \(AO,\s\up6(→))＝eq \(OB,\s\up6(→))＋eq \(OC,\s\up6(→))，所以eq \(AO,\s\up6(→))＝eq \(OM,\s\up6(→))，
则eq \(AO,\s\up6(→))＝eq \f(1,2)eq \(AM,\s\up6(→))＝eq \f(1,4)(eq \(AB,\s\up6(→))＋eq \(AC,\s\up6(→)))＝eq \f(1,4)eq \b\lc\(\rc\)(\a\vs4\al\c1(\(AB,\s\up6(→))＋\f(1,t)\(AD,\s\up6(→))))＝eq \f(1,4)eq \(AB,\s\up6(→))＋eq \f(1,4t)eq \(AD,\s\up6(→)).
由B，O，D三点共线，得eq \f(1,4)＋eq \f(1,4t)＝1，解得t＝eq \f(1,3).
6．在△ABC中，∠A＝60°，∠A的平分线交BC于点D，若AB＝4，且eq \(AD,\s\up6(→))＝eq \f(1,4)eq \(AC,\s\up6(→))＋λeq \(AB,\s\up6(→))(λ∈R)，则AD的长为________．
【答案】：3eq \r(3)
【解析】：因为B，D，C三点共线，所以eq \f(1,4)＋λ＝1，解得λ＝eq \f(3,4)，如图，过点D分别作AC，AB的平行线交AB，AC于点M，N，则eq \(AN,\s\up6(→))＝eq \f(1,4)eq \(AC,\s\up6(→))，eq \(AM,\s\up6(→))＝eq \f(3,4)eq \(AB,\s\up6(→))，因为△ABC中，∠A＝60°，∠A的平分线交BC于点D，所以四边形AMDN是菱形，因为AB＝4，所以AN＝AM＝3，AD＝3eq \r(3).
7．(2020·铜川模拟)在△ABC中，点D是边BC上任意一点，M是线段AD的中点，若存在实数λ和μ，使得eq \(BM,\s\up6(→))＝λeq \(AB,\s\up6(→))＋μeq \(AC,\s\up6(→))，则λ＋μ＝________．
【答案】：－eq \f(1,2).
【解析】：如图，因为点D在边BC上，所以存在t∈R，使得eq \(BD,\s\up6(→))＝teq \(BC,\s\up6(→))＝t(eq \(AC,\s\up6(→))－eq \(AB,\s\up6(→)))．因为M是线段AD的中点，所以eq \(BM,\s\up6(→))＝eq \f(1,2)(eq \(BA,\s\up6(→))＋eq \(BD,\s\up6(→)))＝eq \f(1,2)(－eq \(AB,\s\up6(→))＋teq \(AC,\s\up6(→))－teq \(AB,\s\up6(→)))＝－eq \f(1,2)(t＋1)·eq \(AB,\s\up6(→))＋eq \f(1,2)teq \(AC,\s\up6(→)).
又eq \(BM,\s\up6(→))＝λeq \(AB,\s\up6(→))＋μeq \(AC,\s\up6(→))，所以λ＝－eq \f(1,2)(t＋1)，μ＝eq \f(1,2)t，
所以λ＋μ＝－eq \f(1,2).
8．已知P为△ABC所在平面内一点，eq \(AB,\s\up6(→))＋eq \(PB,\s\up6(→))＋eq \(PC,\s\up6(→))＝0，|eq \(AB,\s\up6(→))|＝|eq \(PB,\s\up6(→))|＝|eq \(PC,\s\up6(→))|＝2，则△ABC的面积为________．
【答案】：2eq \r(3)
【解析】：因为eq \(AB,\s\up6(→))＋eq \(PB,\s\up6(→))＋eq \(PC,\s\up6(→))＝0，所以eq \(AB,\s\up6(→))＝－(eq \(PB,\s\up6(→))＋eq \(PC,\s\up6(→)))．
由平行四边形法则可知，以eq \(PB,\s\up6(→))，eq \(PC,\s\up6(→))为边组成的平行四边形的一条对角线与eq \(AB,\s\up6(→))反向，且长度相等．因为|eq \(AB,\s\up6(→))|＝|eq \(PB,\s\up6(→))|＝|eq \(PC,\s\up6(→))|＝2，所以以eq \(PB,\s\up6(→))，eq \(PC,\s\up6(→))为边的平行四边形为菱形，且除BC外的另一条对角线长为2，所以BC＝2eq \r(3)，∠ABC＝90°，所以S△ABC＝eq \f(1,2)AB·BC＝eq \f(1,2)×2×2eq \r(3)＝2eq \r(3).
9.在平面向量中有如下定理：设点O，P，Q，R为同一平面内的点，则P，Q，R三点共线的充要条件是：存在实数t，使eq \(OP,\s\up6(→))＝(1－t)eq \(OQ,\s\up6(→))＋teq \(OR,\s\up6(→)).试利用该定理解答下列问题：如图，在△ABC中，点E为AB边的中点，点F在AC边上，且CF＝2FA，BF交CE于点M，设eq \(AM,\s\up6(→))＝xeq \(AE,\s\up6(→))＋yeq \(AF,\s\up6(→))，则x＋y＝________.
【答案 eq \f(7,5)
【解析】因为B，M，F三点共线，所以存在实数t，使得eq \(AM,\s\up6(→))＝(1－t)eq \(AB,\s\up6(→))＋teq \(AF,\s\up6(→))，又eq \(AB,\s\up6(→))＝2eq \(AE,\s\up6(→))，eq \(AF,\s\up6(→))＝eq \f(1,3)eq \(AC,\s\up6(→))，所以eq \(AM,\s\up6(→))＝2(1－t)eq \(AE,\s\up6(→))＋eq \f(1,3)teq \(AC,\s\up6(→)).又E，M，C三点共线，所以2(1－t)＋eq \f(1,3)t＝1，得t＝eq \f(3,5).所以eq \(AM,\s\up6(→))＝2(1－t)eq \(AE,\s\up6(→))＋teq \(AF,\s\up6(→))＝eq \f(4,5)eq \(AE,\s\up6(→))＋eq \f(3,5)eq \(AF,\s\up6(→))，所以x＝eq \f(4,5)，y＝eq \f(3,5)，所以x＋y＝eq \f(7,5).
三 解答题
1.经过△OAB重心G的直线与OA，OB分别交于点P，Q，设eq \(OP,\s\up6(→))＝meq \(OA,\s\up6(→))，eq \(OQ,\s\up6(→))＝neq \(OB,\s\up6(→))，m，n∈R，求eq \f(1,n)＋eq \f(1,m)的值．
【答案】见解析
【解析】：设eq \(OA,\s\up6(→))＝a，eq \(OB,\s\up6(→))＝b，则eq \(OG,\s\up6(→))＝eq \f(1,3)(a＋b)，
eq \(PQ,\s\up6(→))＝eq \(OQ,\s\up6(→))－eq \(OP,\s\up6(→))＝nb－ma，
eq \(PG,\s\up6(→))＝eq \(OG,\s\up6(→))－eq \(OP,\s\up6(→))＝eq \f(1,3)(a＋b)－ma＝a＋eq \f(1,3)b.
由P，G，Q共线得，存在实数λ使得eq \(PQ,\s\up6(→))＝λeq \(PG,\s\up6(→))，
即nb－ma＝λa＋eq \f(1,3)λb，
则eq \b\lc\{(\a\vs4\al\c1(－m＝λ\b\lc\(\rc\)(\a\vs4\al\c1(\f(1,3)－m))，,n＝\f(1,3)λ，))消去λ，得eq \f(1,n)＋eq \f(1,m)＝3.
2.已知O，A，B是不共线的三点，且eq \(OP,\s\up6(→))＝meq \(OA,\s\up6(→))＋neq \(OB,\s\up6(→))(m，n∈R)．
(1)若m＋n＝1，求证：A，P，B三点共线；
(2)若A，P，B三点共线，求证：m＋n＝1.
【答案】见解析
【证明】：(1)若m＋n＝1，
则eq \(OP,\s\up6(→))＝meq \(OA,\s\up6(→))＋(1－m)eq \(OB,\s\up6(→))
＝eq \(OB,\s\up6(→))＋m(eq \(OA,\s\up6(→))－eq \(OB,\s\up6(→)))，
所以eq \(OP,\s\up6(→))－eq \(OB,\s\up6(→))＝m(eq \(OA,\s\up6(→))－eq \(OB,\s\up6(→)))，
即eq \(BP,\s\up6(→))＝meq \(BA,\s\up6(→))，
所以eq \(BP,\s\up6(→))与eq \(BA,\s\up6(→))共线．
又因为eq \(BP,\s\up6(→))与eq \(BA,\s\up6(→))有公共点B，
所以A，P，B三点共线．
(2)若A，P，B三点共线，
则存在实数λ，使eq \(BP,\s\up6(→))＝λeq \(BA,\s\up6(→))，
所以eq \(OP,\s\up6(→))－eq \(OB,\s\up6(→))＝λ(eq \(OA,\s\up6(→))－eq \(OB,\s\up6(→)))．
又eq \(OP,\s\up6(→))＝meq \(OA,\s\up6(→))＋neq \(OB,\s\up6(→)).
故有meq \(OA,\s\up6(→))＋(n－1)eq \(OB,\s\up6(→))＝λeq \(OA,\s\up6(→))－λeq \(OB,\s\up6(→))，
即(m－λ)eq \(OA,\s\up6(→))＋(n＋λ－1)eq \(OB,\s\up6(→))＝0.
因为O，A，B不共线，
所以eq \(OA,\s\up6(→))，eq \(OB,\s\up6(→))不共线，
所以eq \b\lc\{(\a\vs4\al\c1(m－λ＝0，,n＋λ－1＝0，))所以m＋n＝1.
向量运算
定义
法则(或几何意义)
运算律
加法
求两个向量和的运算
交换律：a＋b＝b＋a；
结合律：(a＋b)＋c＝a＋(b＋c)
减法
求a与b的相反向量－b的和的运算
a－b＝a＋(－b)
数乘
求实数λ与向量a的积的运算
|λ a|＝|λ||a|，当λ>0时，λa与a的方向相同；
当λ<0时，λa与 a的方向相反；
当λ＝0时，λ a＝0
λ(μ a)＝(λμ)a；
(λ＋μ)a＝λa＋μ_a；
λ(a＋b)＝λa＋λb