（全国通用卷）2022年中考数学第一次模拟考试·

这是一份（全国通用卷）2022年中考数学第一次模拟考试·，文件包含全国通用卷2022年中考数学第一次模拟考试参考答案docx、全国通用卷2022年中考数学第一次模拟考试A4考试版docx、全国通用卷2022年中考数学第一次模拟考试答题卡docx、全国通用卷2022年中考数学第一次模拟考试考试版docx等4份试卷配套教学资源，其中试卷共28页， 欢迎下载使用。
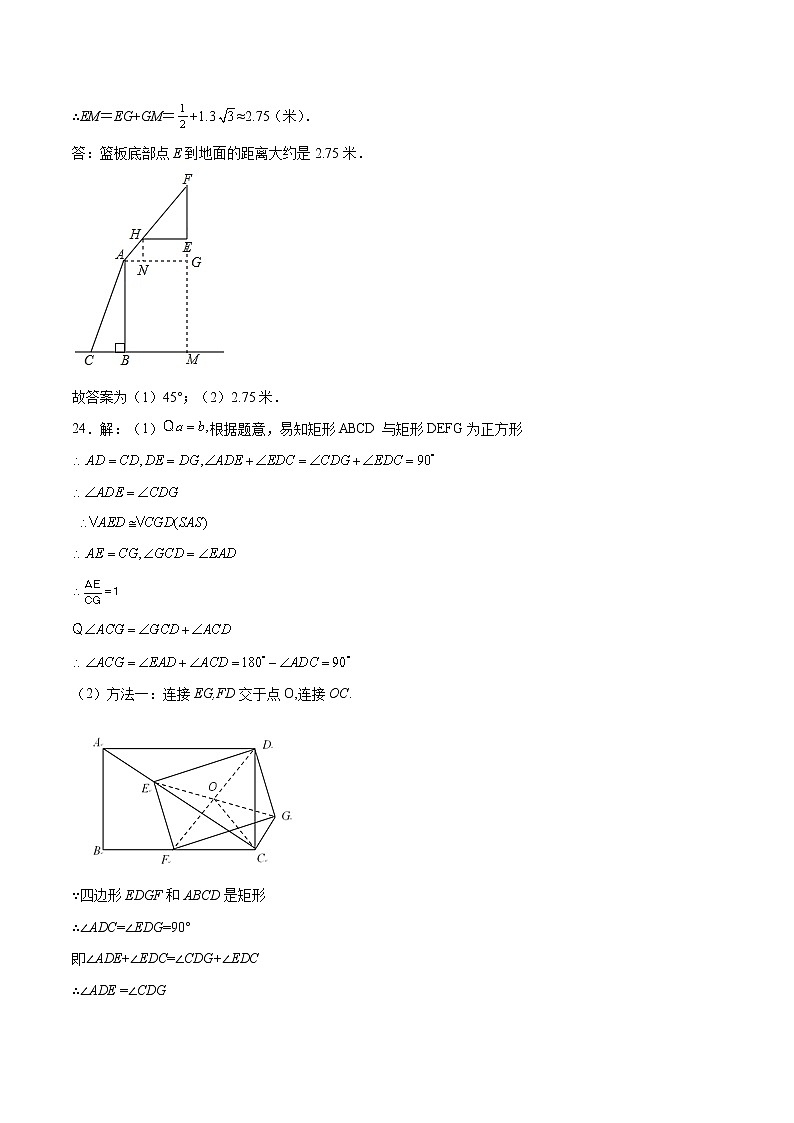
2022年中考数学第一次模拟考试数学·参考答案A卷一、选择题12345678910BDBADDACAC二、填空题11．±          12．        13. 9           14．-2＜a＜115．            16．16              17．9        18．①③三、解答题19．解：原式        20．解：原式= ==＝将代入上式中得： 21．（1）确定甲打第一场∴从其余3位同学中随机选取1位，选中乙同学的概率为故答案为：；（2）树状图如下：共有12种情况，所选2名同学中有甲、乙两位同学的有2种结果∴恰好选中甲、乙两位同学的概率为：．22．（1）设每行驶1千米纯用电的费用为x元，根据题意得：=解得：x=0.26经检验，x=0.26是原分式方程的解，答：每行驶1千米纯用电的费用为0.26元；（2）从A地到B地油电混合行驶，用电行驶y千米，得：0.26y+（﹣y）×（0.26+0.50）≤39解得：y≥74，即至少用电行驶74千米．23．解：（1）在Rt△EFH中，cos∠FHE＝＝＝，∴∠FHE＝45°．答：篮板底部支架HE与支架AF所成的角∠FHE的度数为45°；（2）延长FE交CB的延长线于M，过点A作AG⊥FM于G，过点H作HN⊥AG于N，则四边形ABMG和四边形HNGE是矩形，∴GM＝AB，HN＝EG，在Rt△ABC中，∵tan∠ACB＝，∴AB＝BCtan60°＝1.3×＝1.3（米），∴GM＝AB＝1.3（米），在Rt△ANH中，∠FAN＝∠FHE＝45°，∴HN＝AHsin45°＝×＝（米），∴EM＝EG+GM＝+1.3≈2.75（米）．答：篮板底部点E到地面的距离大约是2.75米．故答案为（1）45°；（2）2.75米．24．解：（1）根据题意，易知矩形ABCD与矩形DEFG为正方形 （2）方法一：连接EG,FD交于点O,连接OC.∵四边形EDGF和ABCD是矩形∴∠ADC=∠EDG=90°即∠ADE+∠EDC=∠CDG+∠EDC∴∠ADE =∠CDG∵∠ BCD=90°OF=OD∴OC=在矩形DEFG中，EG=DF     ∴ OC=∵OE=OG     ∴OE=OC=OG ∴∠OEC=∠OCE   ∠OCF=∠OFC又∵∠OEC+∠ECG+∠EGC=180°∴2∠OCE+2∠OCG =180°∴∠OCE+∠OCG =90°即∠ACG =90°∴∠ECD+∠DCG =90°在Rt△ADC中，∠ECD+∠DAC =90°∴∠DAE=∠DCG∴△DAE∽△DCG       ∴   方法二：过点E作EM⊥BC,EN⊥DC,垂足分别为M和N.∵∠EMC=∠MCN=∠ENC=90°∴四边形EMCN是矩形∴EM=NC,∠MEN=90°.∵∠ ENC =∠ADC=90°∴EN∥AD∴△CEN∽△CAD∴即∵∠MEN=90°∠FED=90°∴∠MEF=∠NED又∵∠END =∠EMF =90°∴△END∽△EMF∴又∵EF=DG∴∵∠ADC=∠EDG=90°∴△ADE∽△CDG∴   ,     ∠DAE=∠DCG       ∵在Rt△ADC中∠DAC+∠ACD=90°∴∠ACG=∠DCG+∠ACD=90°        (3) ∵AD=8,DC=6 ∴AC==10∵DF⊥AC∴，∠CDH +∠ACD=90°∵∠DAC+∠ACD=90°∴∠CDH=∠DAC ∴△ CDH∽△CAD   ∴CD2=CH·CA ,∠CDH=∠CAD ∵CD=6,AC=10∴CH=   ∵ 由（2）知   ∠DEF =∠ADC =90°∴△DEF∽△ADC ∴∠EDH=∠CAD∴∠CDH=∠EDH∵∠DHE=∠DHC=90°DH=DH∴△DHE≌△DHC∴EH=CH=       ∴AE=AC-EH-HC=          ∵∴CG=25．(1)证明：连接OD，如图1所示：∵AD平分∠BAC，∴∠BAD＝∠CAD，∵OA＝OD，∴∠BAD＝∠ODA，∴∠CAD＝∠ODA，∴PD∥AC，∴∠ODB＝∠C＝90°，∴BC⊥OD，又∵OD是圆O的半径，∴BC是圆O的切线；(2)证明：连接DF，如图2所示：∵AE是圆O的直径，∴∠AFE＝90°，∴∠AFE＝∠C＝90°，∴EF∥BC，∴∠AEF＝∠B，∵∠AEF＝∠ADF，∴∠B＝∠ADF，又∵∠BAD＝∠CAD，∴△ABD∽△ADF，∴AB：AD＝AD：AF，∴AD2＝AF•AB；(3)解：在Rt△BOD中，sinB，设圆O的半径为r，则，解得：r＝10，∴AE＝2r＝20，AB＝AE+BE＝36，在Rt△AEF中，∠AFE＝90°，sin∠AEF＝sinB，∴AF，由（2）得：AD2＝AF•AB，∴AD．26．(1)解：由，得点的坐标为，点的坐标为.把，代入抛物线，得，解得，，∴抛物线的解析式为；(2)解：为直角三角形.理由如下：抛物线的对称轴为直线，当时，，∴点的坐标为，当时，，得或5，∴点的坐标为.∵，∴.同理，，，∴，∴为直角三角形；(3)解：存在点M，使AM与直线BC的夹角等于的2倍.分两种情况：①点M在PA左边时，如图，∵，，∴，∴，∵点在直线上，设点的坐标为.根据题意，得，，∴，解得，∴点的坐标为.②点在右边时，如图，此时，∴，∵，∴点是的中点∵，，∴.综上所述，点的坐标为或．