专题2.3 函数的奇偶性、周期性与对称性-2022年高考数学一轮复习核心素养大揭秘学案

这是一份专题2.3 函数的奇偶性、周期性与对称性-2022年高考数学一轮复习核心素养大揭秘学案，文件包含专题23函数的奇偶性周期性与对称性解析版doc、专题23函数的奇偶性周期性与对称性原卷版doc等2份学案配套教学资源，其中学案共27页， 欢迎下载使用。

【考纲要求】
1. 结合具体函数，了解函数奇偶性的含义．
2．能运用函数的图象理解和研究函数的奇偶性．
3．了解函数周期性、最小正周期的含义，会判断、应用简单函数的周期性
【命题趋势】
1. 对函数的奇偶性与周期性的考查主要有两种题型：一是判断函数的奇偶性与周期性，二是已知函数的奇偶性与周期性求值或范围，难度一般．
2．函数的单调性、奇偶性、周期性的综合应用，题型有根据性质判断图象、解不等式、求方程根的个数等，难度较大.
【核心素养】
本讲内容主要考查直观想象、逻辑推理、数学运算的核心素养.
【素养清单•基础知识】
1．函数的奇偶性
函数的定义域关于原点对称是函数具有奇偶性的前提条件．
若f(x)≠0，则奇(偶)函数定义的等价形式如下：
(1)f(－x)＝f(x)⇔f(－x)－f(x)＝0⇔eq \f(f－x,fx)＝1⇔f(x)为偶函数；
(2)f(－x)＝－f(x)⇔f(－x)＋f(x)＝0⇔eq \f(f－x,fx)＝－1⇔f(x)为奇函数．
2．函数的周期性
(1)周期函数
对于函数f(x)，如果存在一个非零常数T，使得当x取定义域内的任何值时，都有f(x＋T)＝f(x)，那么就称函数f(x)为周期函数，称T为这个函数的周期．
周期函数定义的实质：
存在一个非零常数T，使f(x＋T)＝f(x)为恒等式，即自变量x每增加一个T后，函数值就会重复出现一次．
(2)最小正周期
如果在周期函数f(x)的所有周期中存在一个最小的正数，那么这个最小正数就叫做f(x)的最小正周期．
【素养清单•常用结论】
1．函数奇偶性常用结论
(1)如果函数f(x)是奇函数且在x＝0处有定义，则一定有f(0)＝0；如果函数f(x)是偶函数，那么f(x)＝f(|x|)．
(2)奇函数在两个对称的区间上具有相同的单调性；偶函数在两个对称的区间上具有相反的单调性．
(3)在公共定义域内有：奇±奇＝奇，偶±偶＝偶，奇×奇＝偶，偶×偶＝偶，奇×偶＝奇．
2．函数周期性常用结论
对f(x)定义域内任一自变量x：
(1)若f(x＋a)＝－f(x)，则T＝2a(a>0)．
(2)若f(x＋a)＝eq \f(1,fx)，则T＝2a(a>0)．
(3)若f(x＋a)＝－eq \f(1,fx)，则T＝2a(a>0)．
3．函数图象的对称性
(1)若函数y＝f(x＋a)是偶函数，即f(a－x)＝f(a＋x)，则函数y＝f(x)的图象关于直线x＝a对称．
(2)若对于R上的任意x都有f(2a－x)＝f(x)或f(－x)＝f(2a＋x)，则y＝f(x)的图象关于直线x＝a对称．
(3)若函数y＝f(x＋b)是奇函数，即f(－x＋b)＋f(x＋b)＝0，则函数y＝f(x)关于点(b,0)中心对称．
【真题体验】
1.【2019年高考全国Ⅰ卷理数】函数f(x)=在的图像大致为（ ）
A． B．
C． D．
【答案】D
【解析】由，得是奇函数，其图象关于原点对称．
又，可知应为D选项中的图象．
故选D．
【名师点睛】本题考查函数的性质与图象的识别，渗透了逻辑推理、直观想象和数学运算素养．采取性质法和赋值法，利用数形结合思想解题．
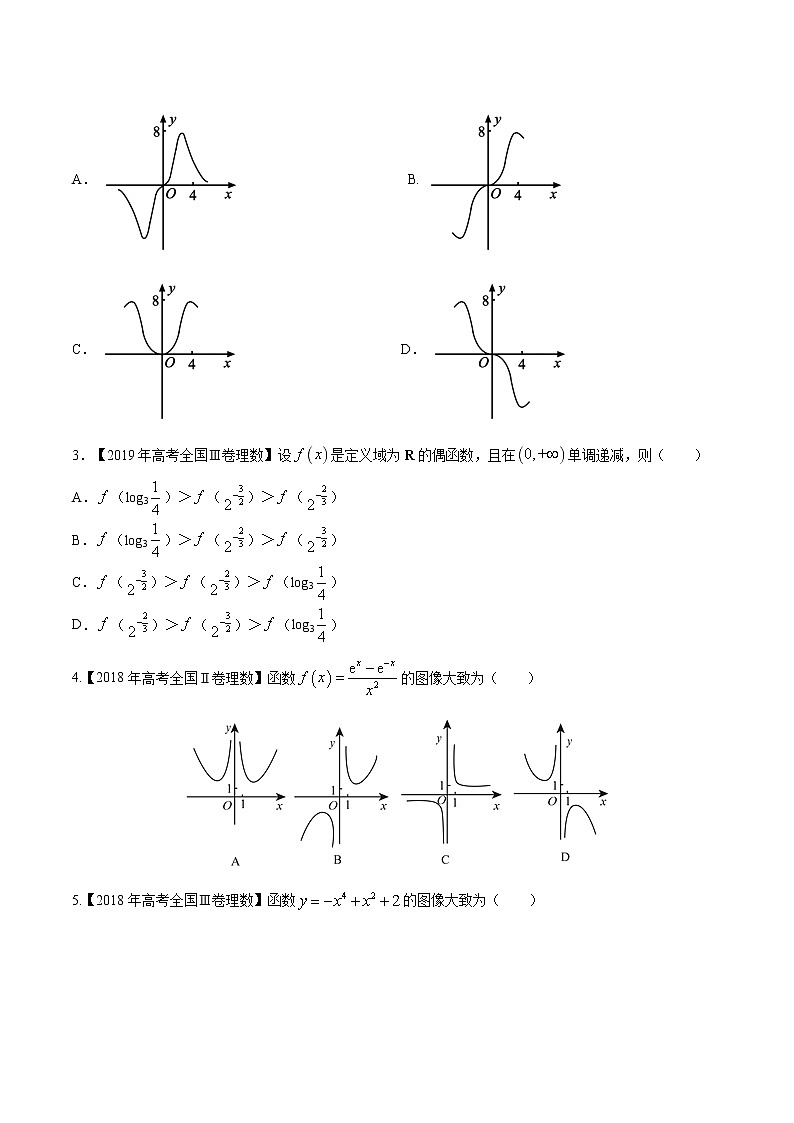
2．【2019年高考全国Ⅲ卷理数】函数在的图像大致为（ ）
A． B.C． D．
【答案】B
【解析】设，则，所以是奇函数，图象关于原点成中心对称，排除选项C．
又排除选项D；
，排除选项A，
故选B．
【名师点睛】本题通过判断函数的奇偶性，排除错误选项，通过计算特殊函数值，作出选择．本题注重基础知识、基本计算能力的考查．
3．【2019年高考全国Ⅲ卷理数】设是定义域为R的偶函数，且在单调递减，则（ ）
A．（lg3）＞（）＞（）
B．（lg3）＞（）＞（）
C．（）＞（）＞（lg3）
D．（）＞（）＞（lg3）
【答案】C
【解析】是定义域为的偶函数，．
，
又在(0，+∞)上单调递减，
∴，
即.
故选C．
【名师点睛】本题主要考查函数的奇偶性、单调性，先利用函数的奇偶性化为同一区间，再利用中间量比较自变量的大小，最后根据单调性得到答案．
4.【2018年高考全国Ⅱ卷理数】函数的图像大致为（ ）

【答案】B
【解析】为奇函数，舍去A；
，∴舍去D；
时，，单调递增，舍去C.
因此选B.
【名师点睛】有关函数图象识别问题的常见题型及解题思路：（1）由函数的定义域，判断图象左右的位置，由函数的值域，判断图象的上下位置；（2）由函数的单调性，判断图象的变化趋势；（3）由函数的奇偶性，判断图象的对称性；（4）由函数的周期性，判断图象的周期性.
5.【2018年高考全国Ⅲ卷理数】函数的图像大致为（ ）

【答案】D
【解析】函数图象过定点，排除A，B；
令，则，
由得，得或，此时函数单调递增，
由得，得或，此时函数单调递减，排除C.
故选D.
【名师点睛】本题主要考查函数的图象的识别和判断，利用函数图象过的定点及由导数判断函数的单调性是解决本题的关键.
6.【2018年高考浙江】函数y=sin2x的图象可能是（ ）
A． B．
C． D．
【答案】D
【解析】令，因为，所以为奇函数，排除选项A,B;
因为时，，所以排除选项C，
故选D．
【名师点睛】先研究函数的奇偶性，再研究函数在上的符号，即可判断选择.有关函数图象的识别问题的常见题型及解题思路：
（1）由函数的定义域，判断图象的左、右位置，由函数的值域，判断图象的上、下位置；
（2）由函数的单调性，判断图象的变化趋势；
（3）由函数的奇偶性，判断图象的对称性；
（4）由函数的周期性，判断图象的周期性．
7.【2018年高考全国Ⅰ卷理数】设函数，若为奇函数，则曲线在点处的切线方程为（ ）
A． B．
C． D．
【答案】D
【解析】因为函数是奇函数，所以，解得，
所以，，
所以，
所以曲线在点处的切线方程为，化简可得，
故选D．
【名师点睛】该题考查的是函数的奇偶性以及有关曲线在某个点处的切线方程的问题，在求解的过程中，首先需要确定函数解析式，此时利用到结论：多项式函数中，奇函数不存在偶次项，偶函数不存在奇次项，从而求得相应的参数值，之后利用求导公式求得，借助于导数的几何意义，结合直线方程的点斜式求得结果.
8．【2018年高考全国Ⅱ卷理数】已知是定义域为的奇函数，满足．若，则（ ）
A． B．0
C．2 D．50
【答案】C
【解析】因为是定义域为的奇函数，且，
所以,
因此，
因为，所以，
因为，从而.
故选C．
【名师点睛】先根据奇函数的性质以及对称性确定函数周期，再根据周期以及对应函数值求结果.函数的奇偶性与周期性相结合的问题多考查求值问题，常利用奇偶性及周期性进行变换，将所求函数值的自变量转化到已知解析式的函数定义域内求解．
【考法拓展•题型解码】
考法一 函数奇偶性的判断
解题技巧：判断函数奇偶性的方法
(1)根据定义判断，首先看函数的定义域是否关于原点对称；在定义域关于原点对称的条件下，再化简解析式，根据f(－x)与f(x)的关系作出判断．
(2)利用函数图象特征判断．
(3)分段函数奇偶性的判断，要分别从x>0或x<0来寻找等式f(－x)＝f(x)或f(－x)＝－f(x)成立，只有当对称的两个区间上满足相同关系时，分段函数才具有确定的奇偶性．
【例1】 (1)设函数f(x)，g(x)的定义域都为R，且f(x)是奇函数，g(x)是偶函数，则下列结论中正确的是( )
A．f(x)g(x)是偶函数 B．|f(x)|g(x)是奇函数
C．f(x)|g(x)|是奇函数 D．|f(x)g(x)|是奇函数
【答案】C
【解析】f(x)为奇函数，g(x)为偶函数，故f(x)g(x)为奇函数，f(x)|g(x)|为奇函数，|f(x)|g(x)为偶函数，|f(x)g(x)|为偶函数．故选C．
(2)判断下列各函数的奇偶性．
①f(x)＝(x＋1)eq \r(\f(1－x,1＋x))； ②f(x)＝eq \f(lg1－x2,|x－2|－2)； ③f(x)＝eq \b\lc\{\rc\ (\a\vs4\al\c1(x2＋x，x<0，,－x2＋x，x>0.))
【答案】见解析
【解析】(2)①由eq \b\lc\{\rc\ (\a\vs4\al\c1(1＋x≠0，,\f(1－x,1＋x)≥0，))得定义域为(－1,1]，关于原点不对称，故f(x)为非奇非偶函数．
②由eq \b\lc\{\rc\ (\a\vs4\al\c1(1－x2>0，,|x－2|≠2，))得定义域为(－1,0)∪(0,1)，关于原点对称．所以x－2<0，所以|x－2|－2＝－x，所以f(x)＝eq \f(lg1－x2,－x).
又因为f(－x)＝eq \f(lg[1－－x2],x)＝－eq \f(lg1－x2,－x)＝－f(x)，所以函数f(x)为奇函数．
③显然函数f(x)的定义域为(－∞，0)∪(0，＋∞)，关于原点对称．
当x<0时，－x>0，则f(－x)＝－(－x)2－x＝－x2－x＝－f(x)；
当x>0时，－x<0，则f(－x)＝(－x)2－x＝x2－x＝－f(x)．
综上可知，对于定义域内的任意x，总有f(－x)＝－f(x)成立，所以函数f(x)为奇函数．
考法二 函数奇偶性的应用
解题技巧：与函数奇偶性有关的问题及解决方法
(1)已知函数的奇偶性求函数值：将待求值利用奇偶性转化为已知区间上的函数值求解．
(2)已知函数的奇偶性求解析式：将待求区间上的自变量转化到已知区间上，再利用奇偶性求出，或充分利用奇偶性构造关于f(x)的方程(组)，从而得到f(x)的解析式．
(3)已知函数的奇偶性求函数解析式中参数的值：常常利用待定系数法，由f(x)±f(－x)＝0得到关于待求参数的恒等式，由系数的对等性得参数的值或对方程求解．
(4)应用奇偶性画图象和判断单调性：利用奇偶性可画出另一对称区间上的图象并判断另一区间上的单调性．
【例2】 (1)已知f(x)，g(x)分别是定义在R上的偶函数和奇函数，且f(x)－g(x)＝x3＋x2＋1，则f(1)＋g(1)＝( )
A．－3 B．－1
C．1 D．3
【答案】C
【解析】用“－x”代替“x”，得f(－x)－g(－x)＝(－x)3＋(－x)2＋1，化简得f(x)＋g(x)＝－x3＋x2＋1，令x＝1，得f(1)＋g(1)＝1.故选C．
(2)函数y＝f(x)是R上的奇函数，当x＜0时，f(x)＝2x，则当x＞0时，f(x)＝( )
A．－2x B．2－x
C．－2－x D．2x
【答案】C
【解析】当x>0时，－x<0，所以f(－x)＝2－x＝－f(x)，所以f(x)＝－2－x.故选C．
(3)若函数f(x)＝xln(x＋eq \r(a＋x2))为偶函数，则a＝__________.
【答案】1
【解析】令g(x)＝ln(x＋eq \r(a＋x2))，则f(x)＝x·g(x)为偶函数，则必有g(x)为奇函数，所以g(0)＝lneq \r(a)＝0，所以a＝1.
考法三 函数的周期性
归纳总结：函数周期性的判断与应用
(1)判断函数的周期性只需证明f(x＋T)＝f(x)(T≠0)便可证明函数是周期函数，且周期为T，函数的周期性常与函数的其他性质综合命题．
(2)根据函数的周期性，可以由函数局部的性质得到函数的整体性质，在解决具体问题时，要注意结论：若T是函数的周期，则kT(k∈Z，且k≠0)也是函数的周期．
【例3】 (1)若f(x)是R上周期为2的函数，且满足f(1)＝1，f(2)＝2，则f(3)－f(4)＝__________.
(2)已知f(x)是定义在R上的函数，并且f(x＋2)＝eq \f(1,fx)，当2≤x≤3时，f(x)＝x，则f(2 022)＝__________.
(3)定义在R上的函数f(x)满足f(x＋6)＝f(x)．当－3≤x<－1时，f(x)＝－(x＋2)2；当－1≤x<3时，f(x)＝x.则f(1)＋f(2)＋f(3)＋…＋f(2 022)＝__________.
【答案】(1)－1 (2)2 (3)337
【解析】 (1)由f(x＋2)＝f(x)可得f(3)－f(4)＝f(1)－f(2)＝1－2＝－1.
(2)由f(x＋2)＝eq \f(1,fx)得f(x＋4)＝eq \f(1,fx＋2)＝f(x)，所以T＝4，f(2 022)＝f(4×505＋2)＝f(2)＝2.
(3)由f(x＋6)＝f(x)可知，函数f(x)的周期为6，由已知条件可得f(1)＝1，f(2)＝2，f(3)＝f(－3)＝－1，f(4)＝f(－2)＝0，f(5)＝f(－1)＝－1，f(6)＝f(0)＝0，所以在一个周期内有f(1)＋f(2)＋f(3)＋…＋f(6)＝1＋2－1＋0－1＋0＝1，所以f(1)＋f(2)＋…＋f(2 022)＝337×1＝337.
考法四 函数性质的综合应用
归纳总结：函数性质综合应用问题的常见类型及解题策略
(1)单调性与奇偶性的综合：注意函数单调性及奇偶性的定义，以及奇、偶函数图象的对称性．
(2)周期性与奇偶性的综合：此类问题多考查求值问题，常用奇偶性及周期性进行变换，将所求函数值的自变量转化到已知解析式的函数定义域内求解．
(3)单调性、奇偶性与周期性的综合：解决此类问题通常先利用周期性转化自变量所在的区间，然后利用奇偶性和单调性求解．
【例4】 (1)已知定义域为(－1,1)的奇函数f(x)是减函数，且f(a－3)＋f(9－a2)<0，则实数a的取值范围是( )
A．(2eq \r(2)，3) B．(3，eq \r(10))
C．(2eq \r(2)，4) D．(－2,3)
【答案】A
【解析】由f(a－3)＋f(9－a2)<0得f(a－3)<－f(9－a2)．又由奇函数性质，得f(a－3)a2－9，))解得2eq \r(2)(2)(2018·全国卷Ⅱ)已知f(x)是定义域为(－∞，＋∞)的奇函数，满足f(1－x)＝f(1＋x)．若f(1)＝2，则f(1)＋f(2)＋f(3)＋…＋f(50)＝( )
A．－50 B．0
C．2 D．50
【答案】C
【解析】因为f(x＋2)＝f[1＋(1＋x)]＝f[1－(1＋x)]＝f(－x)＝－f(x)，所以f(x＋4)＝－f(x＋2)＝f(x)，即f(x)是周期为4的周期函数．又f(x)为奇函数，且x∈R，所以f(0)＝0，f(1)＝2，f(2)＝f(1＋1)＝f(0)＝0，f(3)＝f(1＋2)＝f(1－2)＝f(－1)＝－f(1)＝－2，f(4)＝f(0)＝0，所以f(1)＋f(2)＋f(3)＋f(4)＝0，而50＝4×12＋2，所以f(1)＋f(2)＋f(3)＋…＋f(50)＝f(1)＋f(2)＝2.
(3)(2019·池州联考)已知函数f(x)的定义域为R，且满足下列三个条件：
①∀x1，x2∈[4,8]，当x10；②f(x＋4)＝－f(x)；③y＝f(x＋4)是偶函数．
若a＝f(6)，b＝f(11)，c＝f(2 025)，则a，b，c的大小关系正确的是( )
A．aC．a【答案】B
【解析】由条件①知，当x∈[4,8]时，f(x)为增函数；由条件②知，f(x＋8)＝－f(x＋4)＝f(x)，f(x)是周期为8的周期函数；由条件③知，y＝f(x)关于直线x＝4对称，所以f(11)＝f(3)＝f(5)，f(2 025)＝f(1)＝f(7)，故f(5)＜f(6)＜f(7)，即b＜a＜c.故选B．
【易错警示】
易错点 不会利用函数的奇偶性解抽象不等式
【典例】 (2016·天津卷)已知f(x)是定义在R上的偶函数，且在区间(－∞，0)上单调递增. 若实数a满足f(2|a－1|)＞f(－eq \r(2))，则a的取值范围是__________．
【错解】：由已知f(2|a－1|)＞f(－eq \r(2))可得f(2|a－1|)＞f(eq \r(2))，而f(x)是增函数，所以2|a－1|>eq \r(2)＝2 eq \s\up4(\f(1,2)) ，即|a－1|>eq \f(1,2)，所以a>eq \f(3,2)或a【错因分析】：偶函数f(x)在区间(－∞，0)上是增函数，而偶函数在与原点对称的区间上单调性相反，所以在(0，＋∞)上f(x)是减函数．本解答忽视了奇偶性的基本性质，从而在将抽象不等式转化为具体不等式时出错误．
【正解】：【答案】：eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(1,2)，\f(3,2)))
【解析】因为f(x)是偶函数且在(－∞，0)上单调递增，所以f(x)在(0，＋∞)上单调递减，且f(－eq \r(2))＝f(eq \r(2))，所以原不等式可化为f(2|a－1|)＞f(eq \r(2))，故有2|a－1|＜eq \r(2)，即|a－1|归纳总结：函数不等式的求解方法
解与函数有关的不等式问题，常利用奇函数在对称单调区间上有相同的单调性，偶函数在对称单调区间上有相反的单调性的性质，利用题目已知条件，转化为不等式问题来求解，而解有关抽象函数不等式问题，也是充分利用函数的奇偶性和单调性求解．
【跟踪训练】 已知定义在R上的奇函数f(x)满足：当x>0时，f(x)＝2x－eq \f(2,x)，则eq \f(fx,x)>0的解集为( )
A．(－1,0)∪(0,1)
B．(－1,0)∪(1，＋∞)
C．(－∞，－1)∪(0,1)
D．(－∞，－1)∪(1，＋∞)
【答案】D
【解析】 因为当x>0时，函数f(x)单调递增，又f(1)＝0，所以f(x)＝2x－eq \f(2,x)>0的解集为(1，＋∞)，所以eq \f(fx,x)＞0在(0，＋∞)上的解集为(1，＋∞)．因为f(x)是奇函数，所以eq \f(fx,x)是偶函数，则eq \f(fx,x)>0在R上的解集为(－∞，－1)∪(1，＋∞)．
【递进题组】
1．下列函数中既不是奇函数也不是偶函数的是( )
A．y＝2|x| B．y＝lg(x＋eq \r(x2＋1))
C．y＝2x＋2－x D．y＝lgeq \f(1,x＋1)
【答案】D
【解析】 对于D项，eq \f(1,x＋1)>0，即x>－1，其定义域关于原点不对称，是非奇非偶函数．
2．已知f(x)是定义在R上的奇函数，当x≥0时，f(x)＝3x＋m(m为常数)，则f(－lg35)＝( )
A．－6 B．6
C．4 D．－4
【答案】D
【解析】 因为f(x)是定义在R上的奇函数，且当x≥0时，f(x)＝3x＋m，所以f(0)＝1＋m＝0⇒m＝－1，则f(－lg35)＝－f(lg35)＝－(3lg35－1)＝－4.
3．已知定义在R上的偶函数f(x)，在x≥0时，f(x)＝ex＋ln(x＋1)，若f(a)A．(－∞，1) B．eq \b\lc\(\rc\)(\a\vs4\al\c1(－∞，\f(1,2)))
C．eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(1,2)，1)) D．(1，＋∞)
【答案】B
【解析】 根据题中所给的函数解析式，可知函数在[0，＋∞)上是增函数，根据偶函数图象的对称性，可知函数在(－∞，0)上是减函数，所以f(a)4．(2019·晋中模拟)已知f(x)是R上的奇函数，f(1)＝2，且对任意x∈R都有f(x＋6)＝f(x)＋f(3)成立，则f(2 023)＝__________.
【答案】2
【解析】 因为f(x＋6)＝f(x)＋f(3)，令x＝－3，f(3)＝f(－3)＋f(3)＝－f(3)＋f(3)＝0，所以f(x＋6)＝f(x)＋0＝f(x)，所以T＝6，f(2 023)＝f(337×6＋1)＝f(1)＝2.
【考卷送检】
一、选择题
1．下列函数是奇函数的是( )
A．f(x)＝x|x| B．f(x)＝lg x
C．f(x)＝2x＋2－x D．f(x)＝x3－1
【答案】A
【解析】 对于B项，f(x)＝lg x的定义域是x>0，所以不是奇函数；对于C项，f(－x)＝2－x＋2x＝f(x)，f(x)是偶函数；对于D项，f(x)＝x3－1的定义域为R，但图象不过原点，所以f(x)是非奇非偶函数．只有A项满足定义域关于原点对称，并且f(－x)＝－f(x)，是奇函数．
2．已知f(x)＝3ax2＋bx－5a＋b是偶函数，且其定义域为[6a－1，a]，则a＋b＝( )
A．eq \f(1,7) B．－1
C．1 D．7
【答案】A
【解析】 因为偶函数的定义域关于原点对称，所以6a－1＋a＝0，所以a＝eq \f(1,7).又因为f(x)为偶函数，所以b＝0，即a＋b＝eq \f(1,7).故选A．
3．已知f(x)在R上是奇函数，且满足f(x＋4)＝f(x)，当x∈(0,2)时，f(x)＝2x2，则f(2 019)＝( )
A．－2 B．2
C．－98 D．98
【答案】A
【解析】 因为f(x＋4)＝f(x)，所以f(x)是以4为周期的周期函数，所以f(2 019)＝f(504×4＋3)＝f(3)＝f(－1)．又f(x)为奇函数，所以f(－1)＝－f(1)＝－2×12＝－2，即f(2 019)＝－2.
4．(2019·沈阳测试)设函数f(x)＝ln(1＋x)＋mln(1－x)是偶函数，则( )
A．m＝1，且f(x)在(0,1)上是增函数
B．m＝1，且f(x)在(0,1)上是减函数
C．m＝－1，且f(x)在(0,1)上是增函数
D．m＝－1，且f(x)在(0,1)上是减函数
【答案】B
【解析】 因为函数f(x)＝ln(1＋x)＋mln(1－x)是偶函数，所以f eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(1,2)))＝f eq \b\lc\(\rc\)(\a\vs4\al\c1(－\f(1,2)))，则(m－1)ln 3＝0，即m＝1，则f(x)＝ln(1＋x)＋ln(1－x)＝ln(1－x2)，因为当x∈(0,1)时，y＝1－x2是减函数，故f(x)在(0,1)上是减函数．故选B．
5．(2019·广州模拟)定义在R上的函数f(x)满足f(－x)＝－f(x)，f(x)＝f(x＋4)，且当x∈(－1,0)时，f(x)＝2x＋eq \f(1,5)，则f(lg220)＝( )
A．1 B．eq \f(4,5)
C．－1 D．－eq \f(4,5)
【答案】C
【解析】 因为x∈R，且f(－x)＝－f(x)，所以函数为奇函数．因为f(x)＝f(x＋4)，所以函数的周期为4.故f(lg220)＝f(lg220－4)＝f eq \b\lc\(\rc\)(\a\vs4\al\c1(lg2\f(5,4)))＝－f eq \b\lc\(\rc\)(\a\vs4\al\c1(－lg2\f(5,4)))＝－f eq \b\lc\(\rc\)(\a\vs4\al\c1(lg2\f(4,5)))＝－eq \b\lc\(\rc\)(\a\vs4\al\c1(2lg2 eq \s\up4(\f(4,5)) ＋\f(1,5)))＝－eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(4,5)＋\f(1,5)))＝－1.故选C．
6．(2019·成都八中月考)设函数f(x)＝ln(1＋|x|)－eq \f(1,1＋x2)，则使f(x)＞f(2x－1)成立的x的取值范围是( )
A．eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(1,3)，1)) B．eq \b\lc\(\rc\)(\a\vs4\al\c1(－∞，\f(1,3)))∪(1，＋∞)
C．eq \b\lc\(\rc\)(\a\vs4\al\c1(－\f(1,3)，\f(1,3))) D．eq \b\lc\(\rc\)(\a\vs4\al\c1(－∞，\f(1,3)))∪eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(1,3)，＋∞))
【答案】A
【解析】 由题意知f(－x)＝f(x)，所以函数f(x)是偶函数，当x≥0时，易得函数f(x)＝ln(1＋x)－eq \f(1,1＋x2)是增函数，所以不等式f(x)＞f(2x－1)等价于|2x－1|＜|x|，解得eq \f(1,3)＜x＜1，则x的取值范围是eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(1,3)，1)).
二、填空题
7．已知奇函数f(x)＝eq \b\lc\{\rc\ (\a\vs4\al\c1(2x＋a，x＞0，,4－2－x，x＜0，))则实数a＝________.
【答案】 －4
【解析】 因为函数f(x)为奇函数，则f(－x)＝－f(x)，f(－1)＝－f(1)，所以4－21＝－(21＋a)，解得a＝－4.
8．设定义在[－2,2]上的偶函数f(x)在区间[0,2]上单调递减，若f(1－m)【答案】 eq \b\lc\[\rc\)(\a\vs4\al\c1(－1，\f(1,2)))
【解析】 因为f(x)是偶函数，所以f(－x)＝f(x)＝f(|x|)．所以不等式f(1－m)|m|，,－2≤1－m≤2，,－2≤m≤2，))解得－1≤m9．定义在实数集R上的函数f(x)满足f(x)＋f(x＋2)＝0，且f(4－x)＝f(x)．现有以下三种叙述：
①8是函数f(x)的一个周期；
②f(x)的图象关于直线x＝2对称；
③f(x)是偶函数．
其中正确的序号是________．
【答案】 ①②③
【解析】 由f(x)＋f(x＋2)＝0得f(x＋2)＝－f(x)，即f(x＋4)＝－f(x＋2)＝f(x)，即4是f(x)的一个周期，8也是f(x)的一个周期，由f(4－x)＝f(x)得f(x)的图象关于直线x＝2对称；由f(4－x)＝f(x)与f(x＋4)＝f(x)得f(4－x)＝f(－x)，f(－x)＝f(x)，即函数f(x)为偶函数．
三、解答题
10．(2019·临川一中期中)已知函数f(x)是定义在R上的偶函数，f(0)＝0，当x＞0时，f(x)＝ eq lg\s\d4(\f(1,2)) x.
(1)求函数f(x)的解析式；
(2)解不等式f(x2－1)＞－2.
【答案】 见解析
【解析】 (1)当x＜0时，－x＞0，则f(－x)＝ eq lg\s\d4(\f(1,2)) (－x)．因为函数f(x)是偶函数，所以f(－x)＝f(x)．所以函数f(x)的解析式为f(x)＝eq \b\lc\{\rc\ (\a\vs4\al\c1( eq lg\s\d4(\f(1,2)) x，x＞0，,0，x＝0，, eq lg\s\d4(\f(1,2)) －x，x＜0.))
(2)因为f(4)＝ eq lg\s\d4(\f(1,2)) 4＝－2，f(x)是偶函数，所以不等式f(x2－1)＞－2可化为f(|x2－1|)＞f(4)．又因为函数f(x)在(0，＋∞)上是减函数，所以当x2－1≠0时，0＜|x2－1|＜4，解得－eq \r(5)＜x＜eq \r(5)且x≠±1，当x2－1＝0即x＝±1时，f(x2－1)＝0＞－2.综上，不等式的解集为(－eq \r(5)，eq \r(5))．
11．已知定义在R上的奇函数f(x)有最小正周期2，且当x∈(0,1)时，f(x)＝eq \f(2x,4x＋1).
(1)求f(1)和f(－1)的值；
(2)求f(x)在[－1,1]上的解析式．
【答案】 见解析
【解析】 (1)因为f(x)是周期为2的奇函数，所以f(1)＝f(1－2)＝f(－1)＝－f(1)，所以f(1)＝0，f(－1)＝0.
(2)由题意知f(0)＝0.当x∈(－1,0)时，－x∈(0,1)．由f(x)是奇函数得f(x)＝－f(－x)＝－eq \f(2－x,4－x＋1)＝－eq \f(2x,4x＋1).
综上，在[－1,1]上，f(x)＝eq \b\lc\{\rc\ (\a\vs4\al\c1(\f(2x,4x＋1)，x∈0，1，,－\f(2x,4x＋1)，x∈－1，0，,0，x∈{－1，0，1}.))
12．函数f(x)的定义域为D＝{x|x≠0}，且满足对于任意x1，x2∈D，有f(x1·x2)＝f(x1)＋f(x2)．
(1)求f(1)的值；
(2)判断f(x)的奇偶性并证明你的结论；
(3)如果f(4)＝1，f(x－1)<2，且f(x)在(0，＋∞)上是增函数，求x的取值范围．
【答案】 见解析
【解析】 (1)因为对于任意x1，x2∈D，有f(x1·x2)＝f(x1)＋f(x2)，所以令x1＝x2＝1，得f(1)＝2f(1)，所以f(1)＝0.
(2)f(x)为偶函数，证明如下：f(x)定义域关于原点对称，令x1＝x2＝－1，有f(1)＝f(－1)＋f(－1)，所以f(－1)＝eq \f(1,2)f(1)＝0.令x1＝－1，x2＝x有f(－x)＝f(－1)＋f(x)，所以f(－x)＝f(x)，所以f(x)为偶函数．
(3)依题设有f(4×4)＝f(4)＋f(4)＝2，由(2)知f(x)是偶函数，所以f(x－1)<2等价于f(|x－1|)13．(2019·常德模拟)设f(x)是偶函数，且当x＞0时，f(x)是单调函数，则满足等式f(2x)＝feq \b\lc\(\rc\)(\a\vs4\al\c1(\f(x＋1,x＋4)))的所有x之和为( )
A．8 B．－8
C．4 D．－4
【答案】B
【解析】 因为f(x)是偶函数，f(2x)＝feq \b\lc\(\rc\)(\a\vs4\al\c1(\f(x＋1,x＋4)))，所以f(|2x|)＝feq \b\lc\(\rc\)(\a\vs4\al\c1(\b\lc\|\rc\|(\a\vs4\al\c1(\f(x＋1,x＋4))))).又因为f(x)在(0，＋∞)上为单调函数，所以|2x|＝eq \b\lc\|\rc\|(\a\vs4\al\c1(\f(x＋1,x＋4)))，即2x＝eq \f(x＋1,x＋4)或2x＝－eq \f(x＋1,x＋4)，整理得2x2＋7x－1＝0或2x2＋9x＋1＝0.设方程2x2＋7x－1＝0的两根为x1，x2，方程2x2＋9x＋1＝0的两根为x3，x4，则(x1＋x2)＋(x3＋x4)＝－eq \f(7,2)＋eq \b\lc\(\rc\)(\a\vs4\al\c1(－\f(9,2)))＝－8.
偶函数
奇函数
定义
如果对于函数f(x)的定义域内任意一个x
都有f(－x)＝f(x)，那么函数f(x)是偶函数
都有f(－x)＝－f(x)，那么函数f(x)是奇函数
图象特征
关于y轴对称
关于原点对称