专题13 复合函数的零点问题-2021-2022学年高一数学培优辅导（人教A版必修第一册）

这是一份专题13 复合函数的零点问题-2021-2022学年高一数学培优辅导（人教A版必修第一册），共4页。
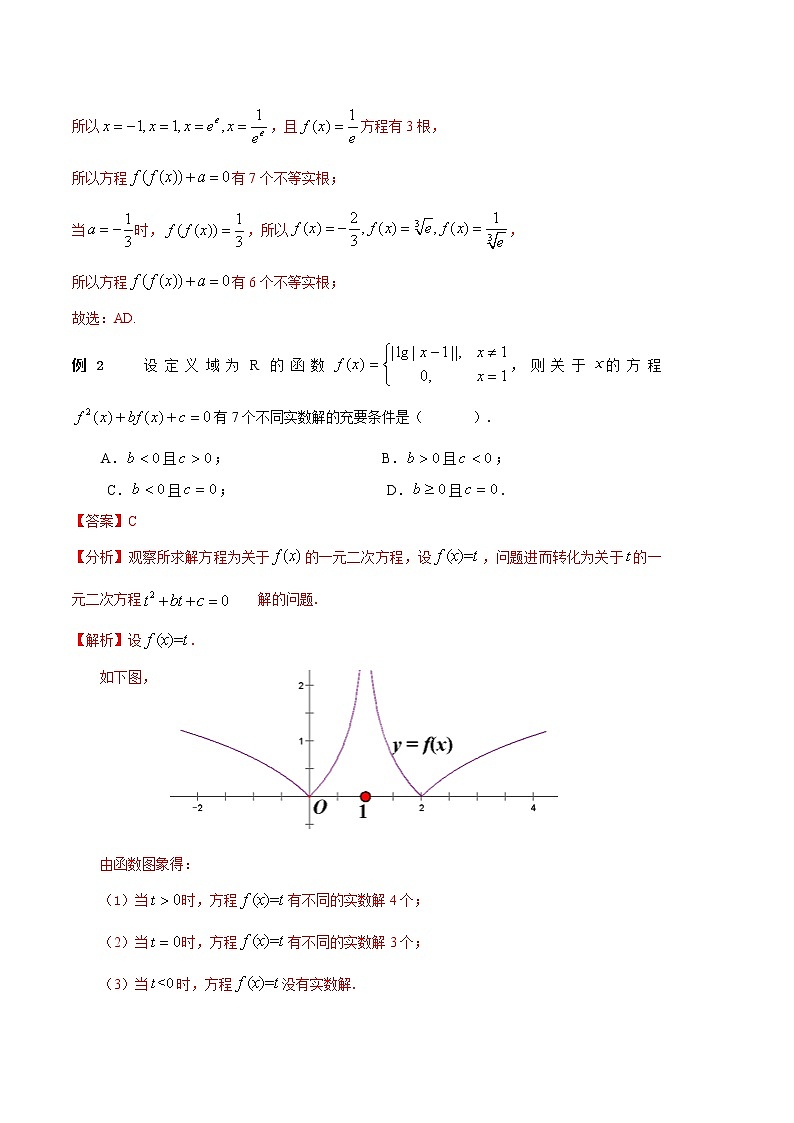
专题13  复合函数的零点问题【方法点拨】复合函数的零点问题一般用换元法,分别探讨内外函数的零点个数或范围即可.【典型例题】例1   已知函数，若方程有6个不等实根，则实数的可能取值是（    ）A． B．0 C． D．【答案】AD【分析】作出函数的图象，结合选项逐一判断即可.【解析】作出函数的图象：    直接验算法：当时，，所以，所以方程有6个不等实根；当时，，所以，所以，所以方程有3个不等实根；当时，，所以，所以，且方程有3根，所以方程有7个不等实根；当时，，所以，所以方程有6个不等实根；故选：AD.例2   设定义域为R的函数，则关于的方程有7个不同实数解的充要条件是（       ）.A．且；                      B．且；C．且；                      D．且.【答案】C【分析】观察所求解方程为关于的一元二次方程，设，问题进而转化为关于的一元二次方程解的问题.【解析】设.如下图，     由函数图象得：（1）当时，方程有不同的实数解4个；（2）当时，方程有不同的实数解3个；（3）当时，方程没有实数解. 所以，关于的方程有7个不同实数解的充要条件是方程有两个根，其中一个根等于0，另一个根大于0.此时应且.【巩固练习】1.已知函数则函数的零点个数是         ．2. 已知函数其中．若函数有3个不同零点，则实数的取值范围是         ．3.已知函数 其中，若函数有3个不同零点，则实数的取值范围是         ．4.设定义在上的函数，若关于的方程有5个不同的实数解，则实数的取值范围是         ．5.若函数（1）函数的零点个数是      ．（2）若函数有3个不同零点，则实数m的取值范围是      ．
【答案与提示】1.【答案】42.【答案】[1，e）3.【答案】(1，e]5.【答案】（1）4；（2）4.【答案】