2021年九年级中考数学考点训练——几何专题：《圆的综合》(2)

这是一份2021年九年级中考数学考点训练——几何专题：《圆的综合》(2)，共20页。试卷主要包含了定义，如图1所示，以点M等内容，欢迎下载使用。
备战2021年九年级中考数学考点训练——几何专题：
《圆的综合》（二）


1．定义：当点P在射线OA上时，把的的值叫做点P在射线OA上的射影值；当点P不在射线OA上时，把射线OA上与点P最近点的射影值，叫做点P在射线OA上的射影值．
例如：如图1，△OAB三个顶点均在格点上，BP是OA边上的高，则点P和点B在射线OA上的射影值均为＝．

（1）在△OAB中，
①点B在射线OA上的射影值小于1时，则△OAB是锐角三角形；
②点B在射线OA上的射影值等于1时，则△OAB是直角三角形；
③点B在射线OA上的射影值大于1时，则△OAB是钝角三角形．
其中真命题有　 　．
A．①②B．①③C．②③D．①②③
（2）已知：点C是射线OA上一点，CA＝OA＝1，以〇为圆心，OA为半径画圆，点B是⊙O上任意点．
①如图2，若点B在射线OA上的射影值为．求证：直线BC是⊙O的切线；
②如图3，已知D为线段BC的中点，设点D在射线OA上的射影值为x，点D在射线OB上的射影值为y，直接写出y与x之间的函数关系式为　 　．




2．在平面直角坐标系xOy中，对于任意两点P1（x1，x2）与P2（x2，y2）的“非常距离”，给出如下定义：若|x1﹣x2|≥|y1﹣y2|，则点P1与点P2的“非常距离”为|x1﹣x2|；若|x1﹣x2|＜|y1﹣y2|，则点P1与点P2的“非常距离”为|y1﹣y2|．
例如：点P1（1，2），点P2（3，5），因为|1﹣3|＜|2﹣5|，所以点P1与点P2的“非常距离”为|2﹣5|＝3，也就是图1中线段P1Q与线段P2Q长度的较大值（点Q为垂直于y轴的直线P1Q与垂直于x轴的直线P2Q的交点）．

（1）已知点A（﹣，0），B为y轴上的一个动点，
①若点A与点B的“非常距离”为2，写出一个满足条件的点B的坐标　 　；
②直接写出点A与点B的“非常距离”的最小值　 　；
（2）已知C是直线y＝x+3上的一个动点，
①如图2，点D的坐标是（0，1），求点C与点D的“非常距离”的最小值及相应的点C的坐标；
②如图3，E是以原点O为圆心，1为半径的圆上的一个动点，求点C与点E的“非常距离”的最小值及相应的点E和点C的坐标．






3．如图，直线l与⊙O相离，OA⊥l于点A，交⊙O于点B，点C是⊙O上一点，连接CB并延长交直线l于点D，使AC＝AD．
（1）求证：AC是⊙O的切线；
（2）若BD＝2，OA＝4，求线段BC的长．





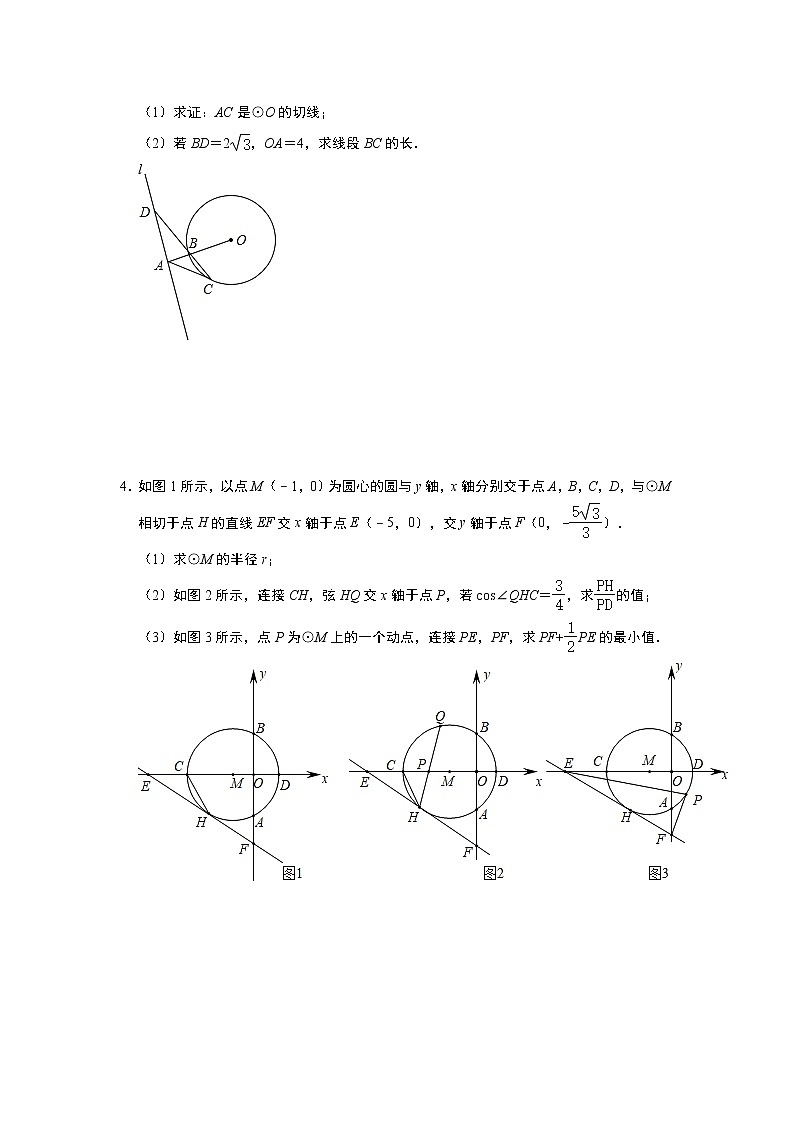
4．如图1所示，以点M（﹣1，0）为圆心的圆与y轴，x轴分别交于点A，B，C，D，与⊙M相切于点H的直线EF交x轴于点E（﹣5，0），交y轴于点F（0，）．
（1）求⊙M的半径r；
（2）如图2所示，连接CH，弦HQ交x轴于点P，若cos∠QHC＝，求的值；
（3）如图3所示，点P为⊙M上的一个动点，连接PE，PF，求PF+PE的最小值．






5．如图，AB＝AC，⊙O为△ABC的外接圆，AF为⊙O的直径，四边形ABCD是平行四边形．
（1）求证：AD是⊙O的切线；
（2）若∠BAC＝45°，AF＝2，求阴影部分的面积．




6．如图，在⊙O中，弦BC垂直于半径OA，垂足为E，D是优弧BC上一点，连接BD，AD，OC，∠ADB＝30°．
（1）求∠AOC的度数；
（2）若弦BC＝8cm，求图中劣弧BC的长．




7．对于平面内的点P和图形M，给出如下定义：以点P为圆心，以r为半径作⊙P，使得图形M上的所有点都在⊙P的内部（或边上），当r最小时，称⊙P为图形M的P点控制圆，此时，⊙P的半径称为图形M的P点控制半径．已知，在平面直角坐标系中，正方形OABC的位置如图所示，其中点B（2，2）．
（1）已知点D（1，0），正方形OABC的D点控制半径为r1，正方形OABC的A点控制半径为r2，请比较大小：r1　 　r2；
（2）连接OB，点F是线段OB上的点，直线l：y＝x+b；若存在正方形OABC的F点控制圆与直线l有两个交点，求b的取值范围．




8．已知⊙O的半径为5，点A、B、C都在⊙O上，∠CAB的平分线交⊙O于点D．
（1）如图1，若BC为⊙O的直径，AB＝6，求AC和BD的长；
（2）如图2，若∠CAB＝60°，过圆心O作OE⊥BD于点E，求OE的长．




9．如图，AB是⊙O的直径，弦CD⊥AB于点H，∠A＝30°，CD＝4，求⊙O的半径的长．





10．矩形ABCD的一边长AB＝4，且BC＞AB，以边AB为直径的⊙O交对角线AC于H，AH＝2，如图，点K为下半圆上一点．
（1）求∠HAB的度数；
（2）求CH的长；
（3）求图中阴影部分的面积；
（4）若圆上到直线AK距离等于3的点有且只有一个，请直接写出线段AK的长．














参考答案
1．解：（1）①错误．点B在射线OA上的射影值小于1时，∠OBA可以是钝角，故△OAB不一定是锐角三角形；
②正确．点B在射线OA上的射影值等于1时，AB⊥OA，∠OAB＝90°，△OAB是直角三角形；
③正确．点B在射线OA上的射影值大于1时，∠OAB是钝角，故△OAB是钝角三角形；
故答案为：C．
（2）①如图2，作BH⊥OC于点H，

∵点B在射线OA上的射影值为，
∴＝，＝，CA＝OA＝OB＝1，
∴＝，
又∵∠BOH＝∠COB，
∴△BOH∽△COB，
∴∠BHO＝∠CBO＝90°，
∴BC⊥OB，
∴直线BC是⊙O的切线；
②图形是上下对称的，只考虑B在直线OC上及OC上方部分的情形．过点D作DM⊥OC，作DN⊥OB，

当∠DOB＜90°时，设DM＝h，
∵D为线段BC的中点，
∴S△OBD＝S△ODC，
∴OB×DN＝OC×DM，
∴DN＝2h，
∵在Rt△DON和Rt△DOM中，
OD2＝DN2+ON2＝DM2+OM2，
∴4h2+y2＝h2+x2，
∴3h2＝x2﹣y2①，
∵BD2＝CD2，
∴4h2+（1﹣y）2＝h2+（2﹣x）2②，
①②消去h得：y＝2x﹣．
如图，当∠BOD＝90°时，过点D作DM⊥OC于点M，

∵D为线段BC的中点，
∴S△OBD＝S△ODC，
∴OB×DO＝OC×DM，
∵CA＝OA＝OB＝1，
∴OD＝2DM，
∴sin∠DOM＝，
∴∠DOM＝30°，
设DM＝h，则OD＝2h，OM＝h，
∴h2+＝1+4h2，
∴h＝，
∴OM＝，
当点B在OC上时，OD＝，
综上所述，当≤x≤时，y＝0；当＜x≤时，y＝2x﹣．
故答案为：y＝0（≤x≤）或y＝2x﹣（＜x≤）．
2．解：（1）①∵B为y轴上的一个动点，
∴设点B的坐标为（0，y）．
∵|﹣﹣0|＝≠2，
∴|0﹣y|＝2，
解得y＝2或y＝﹣2；
∴点B的坐标是（0，2）或（0，﹣2）；
故答案是：（0，2）或（0，﹣2）；
②点A与点B的“非常距离”的最小值为．
故答案是：．

（2）①如图2，取点C与点D的“非常距离”的最小值时，根据运算定义“若|x1﹣x2|≥|y1﹣y2|，则点P1与点P2的“非常距离”为|x1﹣x2|”知：|x1﹣x2|＝|y1﹣y2|．即AC＝AD，
∵C是直线y＝x+3上的一个动点，点D的坐标是（0，1），
∴设点C的坐标为（x0，x0+3），
∴﹣x0＝x0+2，
此时，x0＝﹣，
∴点C与点D的“非常距离”的最小值为：|x0|＝，
此时C（﹣，）；
②当点E在过原点且与直线y＝x+3垂直的直线上时，点C与点E的“非常距离”最小，设E（x，y）（点E位于第二象限）．则，
解得，
故E（﹣，）．
﹣﹣x0＝x0+3﹣，
解得x0＝﹣，
则点C的坐标为（﹣，），最小值为1．

3．（1）证明：连接OC，如图，
∵OB＝OC，AC＝AD
∴∠OBC＝∠OCB，∠ACD＝∠ADC，
∵OA⊥l，
∴∠ADC+∠ABD＝90°，
而∠ABD＝∠OBC，
∴∠OCB+∠ACD＝90°，
∴∠ACO＝90°
∴OC⊥AC，
∴AC是⊙O的切线；
（2）解：如图1，作直径BE，连接CE，
设⊙O半径为r，则AB＝OA﹣OB＝4﹣r，
在Rt△ABD中，∵AD2＝BD2﹣AB2＝12﹣（4﹣r）2，
在Rt△AOC中，∵AC2＝AO2﹣OC2＝16﹣r2，
而AC＝AD，
∴12﹣（4﹣r）2＝16﹣r2，解得r＝，
∵BE为⊙O直径，
∴∠BCE＝90°，
又∵∠ABD＝∠EBC，
∴Rt△ABD∽Rt△CBE，
∴，即，
∴BC＝．


4．解：（1）如图1，连接MH，

∵E（﹣5，0），F（0，﹣），M（﹣1，0），
∴OE＝5，OF＝，EM＝4，
∴在Rt△OEF中，tan∠OEF＝＝，
∴∠OEF＝30°，
∵EF是⊙M的切线，
∴∠EHM＝90°，
∴sin∠MEH＝sin30°＝，
∴MH＝ME＝2，
即r＝2；
（2）如图2，连接DQ、CQ，MH．

∵∠QHC＝∠QDC，∠CPH＝∠QPD，
∴△PCH∽△PQD，
∴，
由（1）可知，∠HEM＝30°，
∴∠EMH＝60°，
∵MC＝MH＝2，
∴△CMH为等边三角形，
∴CH＝2，
∵CD是⊙M的直径，
∴∠CQD＝90°，CD＝4，
∴在Rt△CDQ中，cos∠QHC＝cos∠QDC＝，
∴QD＝CD＝3，
∴；
（3）连MP，取CM的点G，连接PG，则MP＝2，G（﹣2，0），

∴MG＝CM＝1，
∴，
又∵∠PMG＝∠EMP，
∴△MPG∽△MEP，
∴，
∴PG＝PE，
∴PF+PE＝PF+PG，
当F，P，G三点共线时，PF+PG最小，连接FG，即PF+PE有最小值＝FG，
在Rt△OGF中，OG＝2，OF＝，
∴FG＝＝＝．
∴PF+PE的最小值为．
5．解：（1）∵AB＝AC，
∴＝，
∵AF为⊙O的直径，
∴AF⊥BC，
∵四边形ABCD是平行四边形，
∴AD∥BC，
∠AD⊥AF，
∴AD是⊙O的切线；
（2）连接OC，OB，
∵∠BAC＝45°，
∴∠BOC＝90°，
∵AF＝2，
∴OB＝OC＝1，
∴BC＝，
∵四边形ABCD是平行四边形，
∴AD＝BC＝，
连接OE，
∵AB∥BD，
∴∠ACE＝∠BAC＝45°，
∴∠AOE＝2∠ACE＝90°，
∵OA＝OE＝1，
∴阴影部分的面积＝S梯形AOED﹣S扇形AOE＝（1+）×1﹣＝﹣．

6．解：（1）连接OB，
∵OA⊥BC，
∴＝，
∴∠AOC＝∠AOB，
由圆周角定理得，∠AOB＝2∠ADB＝60°，
∴∠AOC＝∠AOB＝60°；
（2）∵OA⊥BC，
∴BE＝BC＝4，
在Rt△BOE中，∠AOB＝60°，
∴OB＝＝，
∴劣弧BC的长＝＝π（cm）．

7．解：（1）由题意得：r1＝BD＝CD＝＝，r2＝AC＝＝2，
∴r1＜r2，
故答案为：＜．
（2）如图所示：⊙O和⊙B的半径均等于OB，

当直线l：y＝x+b与⊙O相切于点M时，连接OM，则OM⊥l，
则直线OM的解析式为：y＝﹣x，
设M（x，﹣x），
∵OM＝OB，
∴OM＝＝，
∴x2+＝8，
解得：x＝﹣或x＝（舍），
∴﹣x＝，
∴M（﹣，），
将M（﹣，）代入y＝x+b得：＝×（﹣）+b，
解得：b＝4．
当直线l：y＝x+b与⊙B相切于点N时，连接BN，则BN⊥l，
同理，设直线BN的解析式为：y＝﹣x+n，将B（2，2）代入得：
2＝﹣×2+n，
∴n＝2+，
∴直线BN的解析式为：y＝﹣x+2+，
设N（m，﹣m+2+），
∵BN＝OB，
∴＝，
∴4﹣4m+m2+﹣+＝8
∴m2﹣4m+2＝0，
∴m＝2﹣（舍）或m＝2+，
∴﹣m+2+＝﹣（2+）+2+＝2﹣，
∴N（2+，2﹣），
∴将N（2+，2﹣）代入y＝x+b得：2﹣＝（2+）+b，
解得：b＝，
∴存在正方形OABC的F点控制圆与直线l有两个交点，此时b的取值范围为：＜b＜．
8．解：（1）如图1，∵BC为⊙O的直径，
∴BC＝10，且∠BAC＝∠BDC＝90°，
则在Rt△ABC中，BC＝10，AB＝6，
∴，
又∵AD是∠CAB的平分线
∴∠CAD＝∠BAD，
∴，
∴CD＝BD，
∴△BDC是等腰直角三角形，
∵BC＝10
∴；
（2）如图2，连接BO，DO，
∵AD是∠CAB的平分线，∠CAB＝60°，
∴∠BAD＝30°，
∴∠BOD＝2∠BAD＝60°，
又∵OB＝OD，
∴△BOD是等边三角形，
又∵OE⊥BD，
∴∠BOE＝30°，BE＝BD，
又∵OB＝5，
∴，
∴．

9．解：连接BC，如图所示：
∵AB是⊙O的直径，弦CD⊥AB于H，
∴∠ACB＝90°，CH＝DH＝CD＝2，∠AHC＝90°，
∵∠A＝30°，
∴AC＝2CH＝4，
在Rt△ABC中，∠A＝30°，
∴AC＝BC＝4，AB＝2BC，
∴BC＝4，AB＝8，
∴OA＝4，
即⊙O的半径长是4．

10．解：（1）连接OH，
∵AB为⊙O的直径，
∴∠AHB＝90°，
∵AB＝4，AH＝2，
∴OA＝OH＝AH，
∴∠HAB＝60°；
（2）∵四边形ABCD是矩形，
∴∠ABC＝90°，
又∠BAH＝60°，
∴∠ACB＝30°，
∴AC＝2AB＝8，
∴CH＝AC﹣AH＝6；
（3）过H作HE⊥AO于E，
∵∠HAB＝60°，AH＝2，
∴HE＝AH＝，
∵AC＝8，CD＝AB＝4，
∴AD＝＝4，
∴图中阴影部分的面积＝S△ABC﹣（S扇形HAO﹣S△AOH）＝×4﹣（﹣）＝9﹣π；
（4）过O作MN⊥AK于N．交⊙O于M，由题意可知MN＝3，
∵OM＝OA＝2，
∴ON＝1，
∴AN＝＝，
∴AK＝2AN＝2．