北师大版数学六年级下 第六讲 正比例与反比例 基础版（教师版+学生版）学案

这是一份北师大版数学六年级下 第六讲 正比例与反比例 基础版（教师版+学生版）学案，文件包含教培专用北师大版数学六年级下第六讲正比例与反比例基础版教师版docx、教培专用北师大版数学六年级下第六讲正比例与反比例基础版学生版docx等2份学案配套教学资源，其中学案共29页， 欢迎下载使用。

第6讲 正比例与反比例
知识点一：变化的量
1.相互关联的变量在一定条件下的变化是有规律的。
2.列表与画图都可以表示变量之间的变化关系。分析表格时，要弄清两个变量及相对应的数据；分析图时，要弄清图中横轴、纵轴表示的量的名称，以及图中每一个点所对应的两个量的多少。
3. 一般用含有字母的式子表示有规律的变量的变化规律，应先根据题中的条件写出等量关系式，再将等量关系式用字母表示出来。[来源:学科网]
知识点二：正比例
1.成正比例的量的特征：一个量随着另一个量的变化而变化，在变化过程中这两个量的比值一定。
2.如果用x和y表示两个相关联的量，用k（一定）表示它们的比值，正比例关系可以表示为yx=k（一定）。
3.判断两个量是否成正比例的方法（1）首先，要确定这两个量是不是相关联的量（其中一个量是否随着另一个量的变化而变化）；（2）其次，要根据两个变量之间的数值对应关系，计算出两个变量每一对数值的比值；（3）最后，根据比值是否一定来判断这两个变量是否成正比例。
知识点三：正比例图像
1.成正比例的两个量表示的各点在同一条直线上，即正比例图象的特征是一条直线。
2.从正比例图象中可以得出任意一点所表示的意义。
3. 观察正比例图象时，要先明确横轴、纵轴表示的意义，从图象中可以直观地看出两个量的变化情况，不需要计算，由一个量的值可以直接找到与它对应的另一个量的值。
知识点四：反比例
1.成反比例的量的特征：一个量随着另一个量的变化而变化，在变化过程中这两个量的积一定。
2.如果用字母x和y表示两个相关联的量，用k（一定）表示它们的乘积，反比例关系可以表示为xy=k（一定）。
3.判断两个量是否成反比例的方法
（1）首先，要确定这两个量是不是相关联的量（其中一个量是否随着另一个量的变化而变化）；
（2）其次，要根据两个变量之间的数值对应关系，计算出两个变量每一对数值的积；
（3）最后，根据积是否一定来判断这两个变量是否成反比例。
4. 正比例和反比例的异同点

考点1：变化的量
【典例1】（磐石市期末）花篮里玫瑰花和百合花枝数的比是4：5，玫瑰花比百合花少()()，百合花比玫瑰花多　25　%．
【分析】花篮里玫瑰花和百合花枝数的比是4：5，即将总数量当作单位“1”，其中玫瑰花有4份，百合花有5份，所以玫瑰花比百合花少5﹣4份，根据求一个数是另一个数的百分之几得出：玫瑰花比百合花少（5﹣4）÷5；百合花比玫瑰花多（5﹣4）÷4．
【解答】解：（5﹣4）÷5；
＝1÷5
=15
（5﹣4）÷4
＝1÷4
＝25%
答：玫瑰花比百合花少15，百合花比玫瑰花多25%．
故答案为：15，25．
【点评】求一个数是另一个数的几分之几，用除法．
【典例2】（简阳市 期中）鸡的数量与鸭的数量比是3：7，鸡的数量是鸭的()()；鸭的数量占鸡和鸭总数量的()()。
【分析】鸡的数量与鸭的数量比是3：7，把鸡的只数看作3，则鸭的只数就是7；总只数是3+7＝10（只），求鸡是鸭的几分之几，用鸡的只数除以鸭的只数；求鸭的数量占鸡和鸭总数量的几分之几，用鸭的数量除以鸡和鸭的总数量即可。
【解答】解：把鸡的只数看作3，则鸭的只数就是7；总只数是3+7＝10（只）
3÷7=37
7÷（3+7）=710
答：鸡的数量与鸭的数量比是3：7，鸡的数量是鸭的37；鸭的数量占鸡和鸭总数量的710。
【点评】此题是考查比的意义和应用，根据求一个数是另一个数的几分之几，用这个数除以另一个数计算。
考点2：正反比例的辨识
【典例1】（怀远县）如图表示一列动车行驶的时间和路程的关系，这列动车每小时行驶　5　千米，路程和时间成　正　比例．

【分析】根据图象是一条过原点的直线，可知这列动车行驶的时间和路程成正比例，也就是它们的比值相等，由此解答即可．
【解答】解：5÷1＝10÷2＝15÷3，所以这列动车每小时行驶5千米，
因为图中是一条直线，所以这列动车行驶的路程和时间成正比例．
【点评】此题更进一步考查辨识成正比例的量，注意平时基础知识的积累
【典例2】（綦江区期末）如果ab﹣8＝17，那么a和b成反比例．　√　（判断对错）
【分析】判断两个相关联的量之间成什么比例，就看这两个量是对应的比值一定，还是对应的乘积一定；如果是比值一定，就成正比例；如果是乘积一定，则成反比例。
【解答】解：如果ab﹣8＝17，即ab＝25（一定），乘积一定，那么a和b成反比例；所以原题说法正确。
故答案为：√。
【点评】此题属于辨识成正、反比例的量，就看这两个量是对应的比值一定，还是对应的乘积一定，再做判断。
考点3：作比例图像
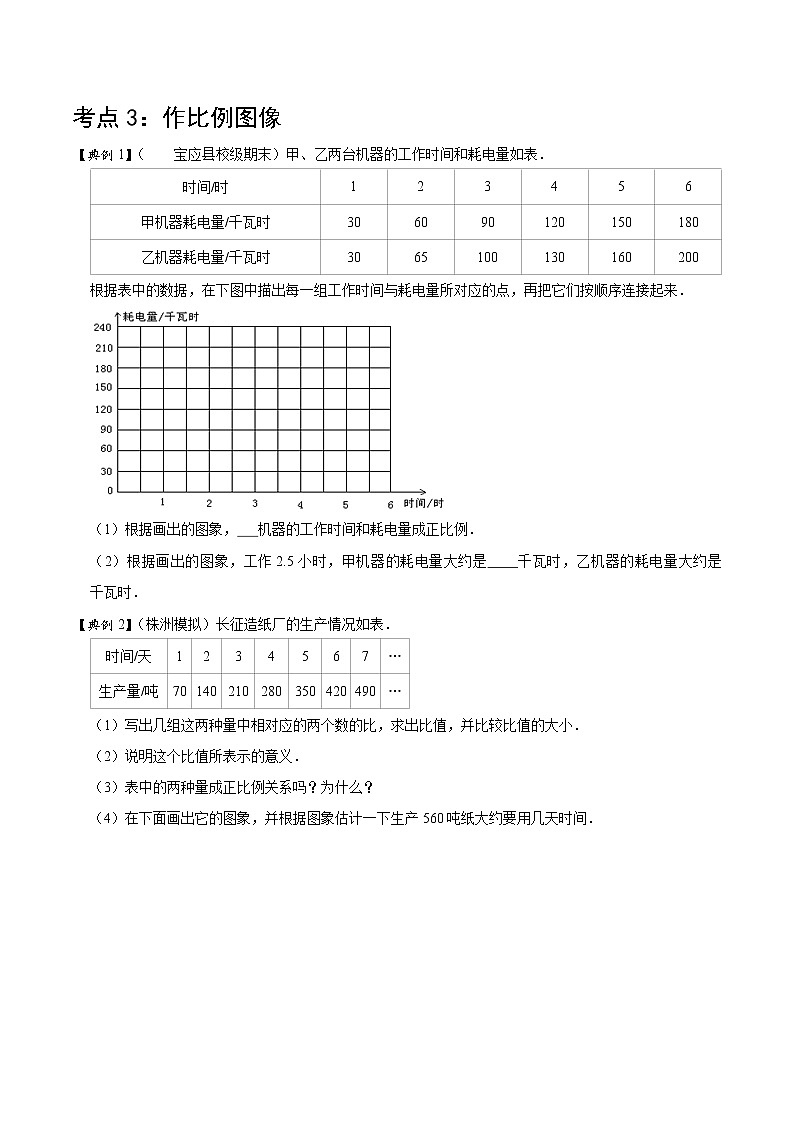
【典例1】（ 宝应县校级期末）甲、乙两台机器的工作时间和耗电量如表．
时间/时
1
2
3
4
5
6
甲机器耗电量/千瓦时
30
60
90
120
150
180
乙机器耗电量/千瓦时
30
65
100
130
160
200
根据表中的数据，在下图中描出每一组工作时间与耗电量所对应的点，再把它们按顺序连接起来．

（1）根据画出的图象，　甲　机器的工作时间和耗电量成正比例．
（2）根据画出的图象，工作2.5小时，甲机器的耗电量大约是　75　千瓦时，乙机器的耗电量大约是　82.5　千瓦时．
【分析】先根据统计表中数据，先分别进行描点，再按图示进行依次连线即可；
（1）根据画出的图象，折线在上升过程中成直线上升的就是机器的工作时间和耗电量成正比例的量．进而判定；
（2）根据画出的图象估计，工作时间在2小时与3小时中间对应的耗电量，就是甲或乙工作2.5小时各自耗电量．
【解答】解：先根据统计表中数据，先分别进行描点，再按图示进行依次连线即可；如图：

（1）根据画出的图象，折线在上升过程中各点的连线成一条直线上升的就是机器的工作时间和耗电量成正比例的量，所以甲机器的工作时间和耗电量成正比例，
（2）根据画出的图象估计，工作时间在2小时与3小时中间对应的耗电量，就是甲或乙工作2.5小时各自耗电量；
所以：甲工作2.5小时耗电量：大约75千瓦时，乙工作2.5小时耗电量：大约82.5千瓦时，
故答案为：甲；75，82.5．
【点评】本题考查的根据统计表中数据画折线统计图的方法的运用．读懂统计图，从统计图中得到必要的信息是解决问题的关键．
【典例2】（株洲模拟）长征造纸厂的生产情况如表．
时间/天
1
2
3
4
5
6
7
…
生产量/吨
70
140
210
280
350
420
490
…
（1）写出几组这两种量中相对应的两个数的比，求出比值，并比较比值的大小．
（2）说明这个比值所表示的意义．
（3）表中的两种量成正比例关系吗？为什么？
（4）在下面画出它的图象，并根据图象估计一下生产560吨纸大约要用几天时间．
【分析】（1）70：1＝70，140：2＝70，210：3＝70，280：4＝70，350：5＝70，它们的比值都是70；
（2）这个比值是用工作量除以工作时间所得，所以这个比值表示工作效率；
（3）因为表中相关联的两种量：工作量：工作时间＝工作效率（一定）符合正比例的意义，所以表中相关联的两种量成正比例关系；
（4）根据统计表，画出图象，然后再估计生产560吨纸大约要的天数即可．
【解答】解：（1）70：1＝70，140：2＝70，210：3＝70，280：4＝70，350：5＝70，它们的比值都是70；
（2）这个比值是用工作量除以工作时间所得，所以这个比值表示工作效率；
（3）因为表中相关联的两种量：工作量：工作时间＝工作效率（一定）符合正比例的意义，
所以表中相关联的两种量成正比例关系；
（4）

估计图象可得，生产560吨纸大约要用8天时间．
【点评】本题考查了正比例的意义的理解和灵活应用．同时考查了学生分析解决问题的能力．





综合练习
一．解答题
1．（蓬溪县期中）若甲乙两数的比是6：5，则甲数是乙数的()()。
【分析】甲乙两数比是6：5，把甲数看成6，乙数就是5，用甲数除以乙数即可求出甲数是乙数的几分之几。
【解答】解：甲乙两数比是6：5，把甲数看成6，乙数就是5
6÷5=65
答：甲数是乙数的65。
故答案为：65。
【点评】本题主要考查了比的意义，然后根据求一个数是另一个数的几分之几，用除法计算。
2．（雁塔区期中）铅笔每支0.5元．把下表填完整．个总价/元
数量/支
1
2
3
4
5
……
总价/元
0.5
1
1.5
2
2.5
……
（1）把铅笔支数与总价所对应的点在图中描述出来，并顺次连接．
（2）总价与支数成　正　比例．
（3）聪聪买铅笔花的钱是明明的3倍，聪聪买铅笔的支数是明明的　3　倍．

【分析】（1）根据表中的数据，在如下图中描出数量和总价所对应的点，再把它们按顺序连起来；
（2）因总价支数=单价（一定），所以总价和支数成正比例；
（3）因为单价一定，所以总价与数量成正比例，由此解答。
【解答】解：（1）

（2）因为总价数量=单价（一定），所以总价和支数成正比例；
（3）因为总价与数量成正比例，聪聪买铅笔花的钱是明明的3倍，
所以聪聪买的铅笔支数是明明的3倍。
故答案为：，正，3。
【点评】解答此题的关键利用图中已知的信息，结合给出的条件，求得各部分数据解决问题。
3．（ 中原区期末）一个长方形的周长为20厘米，若长是9厘米，则宽是1厘米．请先填写如表，然后判断这个长方形在周长不变的情况下，长和宽是否成反比例，并说明理由．
长/cm
9
8
7
6
5
宽/cm
1




【分析】判断两个相关联的量之间成什么比例，就看这两个量是对应的比值一定，还是对应的乘积一定；如果是比值一定，就成正比例；如果是乘积一定，则成反比例．
【解答】解：根据长方形的周长为20厘米，可知长+宽＝10厘米，填下表格如下：
长/cm
9
8
7
6
5
宽/cm
1
2
3
4
5
长+宽＝10（一定），和一定，所以在周长不变的情况下，长和宽不成比例关系．
【点评】本题主要考查辨识成正比例的量和成反比例的量．
4．（ 方城县期中）李叔叔新买了一辆汽车，在试车过程中记录了如表的数据．
所行的路程/km
15
30
45
60
耗油量L
2
4
6
8
（1）根据表中数据，在下图中描出所行路程和耗油量对应的点，再把它们按顺序连起来．
（2）所行路程和耗油量成　正　比例．
（3）根据图象判断，这辆汽车耗油5升行　37.5　km．

【分析】（1）根据统计表中的数据完成统计图．
（2）判断两个相关联的量之间成什么比例，就看这两个量是对应的比值一定，还是对应的乘积一定；如果是比值一定，就成正比例；如果是乘积一定，则成反比例；由此解答即可．
（3）根据图象，观察纵轴5L所对应的横轴的数据，即可得出结论．
【解答】解：（1）画图如下：

（2）15÷2＝30÷4＝45÷6＝60÷8＝7.5（一定），即：汽车行驶的路程÷耗油量＝每升油行驶的路程（一定），
所以这辆汽车行驶的路程和耗油量成正比例．
（3）观察图表，这辆汽车耗油5升行37.5km．
故答案为：正，37.5．
【点评】此题属于辨识成正、反比例的量，就看这两个量是对应的比值一定，还是对应的乘积一定，再做判断．
5．（ 雁塔区期中）一台榨油机的生产情况如表所示．
时间/时
1
2
3
4
5
6
产量/吨
4
8
12
16
20
24
①判断产量与时间成什么比例，并说明理由．
②把表中时间和产量所对应的点描在右面的方格纸上，再顺次连接．
③生产4.5时可以榨油　18　吨．

【分析】①根据所给数据可知，产量和时间之间的关系：1：4＝2：8＝3：12＝……＝6：24=14，即其比值一定，所以产量与时间成正比例．
②根据统计表中的数据，作折线统计图即可．
③利用产量和时间之间的正比例关系做题，4.5÷14=18（吨）．
【解答】解：①产量和时间之间的关系：
1：4＝2：8＝3：12＝……＝6：24=14
即其比值一定
答：产量与时间成正比例．
②如图所示，折线统计图：

③4.5÷14=18（吨）
答：生产4.5时可以榨油18吨．
故答案为：18．
【点评】本题主要考查正比例和反比例的意义，关键根据所给数据，判断出产量和时间之间的比例关系．
6．（郴州模拟）一些长方形的长与宽的长度变化如下表．
长/厘米
5
7.5
10
12.5
15
17.5
…
宽/厘米
2
3
4
5
6
7
…
（1）若长方形的宽是8厘米，长是　20　厘米；若长是8厘米，宽是　3.2　厘米．
（2）这些长方形的宽与长成　正　比例．如果用y表示长，x表示宽，则y＝　2.5x　．
（3）这样的长方形中，当周长是70厘米时，它的长和宽各是多少？（列式解答）
【分析】（1）根据表中的数据可知，5：2＝7.5：3＝10：4＝12.5：6＝15：6…＝2.5，说明这些长方形的长与宽的比值一定，所以这些长方形的宽与长成正比例；再根据题意，用y表示长，x表示宽，则y＝2.5x；
根据y＝2.5x，列式求得若长方形的宽是8厘米，长的厘米数；若长是8厘米，宽的厘米数；
（2）根据表中的数据可知，5：2＝7.5：3＝10：4＝12.5：6＝15：6…＝2.5，说明这些长方形的长与宽的比值一定，所以这些长方形的宽与长成正比例；再根据题意，用y表示长，x表示宽，则y＝2.5x；
（3）因为长方形的周长＝（长+宽）×2，可设宽为x厘米，则长为2.5x厘米，列并解方程求得长和宽即可．
【解答】解：（1）当宽是8厘米，长是：2.5×8＝20（厘米），
当长是8厘米，宽是：8÷2.5＝3.2（厘米）；

（2）因为5：2＝7.5：3＝10：4＝12.5：6＝15：6…＝2.5（一定），
是对应的比值一定，所以这些长方形的宽与长成正比例，
如果用y表示长，x表示宽，则y＝2.5x；

（3）宽为x厘米，则长为2.5x厘米，由题意得，
（x+2.5x）×2＝70
3.5x＝35
x＝10
长是：2.5×10＝25（厘米）；
答：它的长是25厘米，宽是10厘米．
故答案为：20，3.2，正，2.5x．
【点评】解决此题关键是先根据表中的数据辨识这些长方形的长与宽成什么比例，再根据长与宽的关系进一步解决其它的问题．
7．（汉寿县期中）已知x与y成反比例关系，在下表的空格中填写合适的数．
x
2
3


y

4
0.6
12
【分析】两种相关联的量，一种量变化，另一种量也随着变化，如果这两种量中相对应的两个数的积一定，这两种量就叫做成反比例的量，它们的关系叫做反比例关系．用字母表示x×y＝k（一定）．
由x与y成反比例关系，根据已知的x＝3，y＝4求出乘积（定值）12，再利用“积÷一个因数＝另一个因数”计算填表即可．
【解答】解：3×4＝12
12÷2＝6
12÷0.6＝20
12÷12＝1
x
2
3
20
1
y
6
4
0.6
12
故答案为：20，1，6．
【点评】知道成反比例关系的两个量的乘积一定，求出定值12，利用“积÷一个因数＝另一个因数”计算是解题的关键．
二．选择题
8．（兴仁市校级期末）王大伯家养白兔和灰兔共40只，它们的数量比可能是（　　）
A．3：1 B．5：1 C．2：5
【分析】由题意可知：白兔和灰兔的数量比的前项与后项的和，应该能整除40，据此即可进行选择。
【解答】解：选项A，3+1＝4，能整除40，故符合要求；
选项B，5+1＝6，不能整除40，故不符合要求；
选项C，2+5＝7，不能整除40，故不符合要求；
故选：A。
【点评】明白“比的前项与后项的和需整除40”是解答本题的关键。
9．（拜泉县期末）如果科技书和文艺书本数的比是3：4，那么下面的说法正确的是（　　）
A．文艺书比科技书多14
B．科技书比文艺书少13
C．科技书占全部书的47
D．文艺书比科技书多全部书的17
【分析】科技书和文艺书本数的比是3：4，把文艺书的本数看作4份，则科技书本数就为3份，根据各选项的说法分别求得正确答案后选择即可．
【解答】解：A、文艺书比科技书多（4﹣3）÷3=13，原题说法错误；
B、科技书比文艺书少（4﹣3）÷4=14，原题说法错误；
C、科技书占全部书的3÷（3+4）=37，原题说法错误；
D、文艺书比科技书多全部书的43+4−33+4=17，原题说法正确；
故选：D．
【点评】求一个数比另一个数多（或少）几分之几的应用题，用除法计算．
10．（白云区期末）大圆和小圆的半径比是2：1，它们的面积比是（　　）
A．1：1 B．2：1 C．4：1 D．8：1
【分析】据大圆与小圆半径的比是2：1，可把大圆的半径看作2份数，小圆的半径看作1份数；进而根据圆的面积＝πr2，分别求出大圆的面积和小圆的面积，然后根据题意，写出比即可。
【解答】解：（π×22）：（π×12）
＝4π：π
＝4：1
答：它们的面积比也是4：1。
故选：C。
【点评】解答此题应明确：两个圆的半径的比，等于直径的比，等于周长的比，两个圆的面积的比，等于两个圆半径的平方的比。
11．（綦江区期末）如图，阴影部分的面积是圆面积的18，是平行四边形面积的16，那么图中圆与平行四边形的面积的最简整数比是（　　）

A．18：16 B．4：3 C．3：4 D．5：7
【分析】令阴影部分的面积是1，那么圆面积的18=平行四边形面积的16=1，由此求出圆的面积和平行四边形的面积，然后作比化简即可。
【解答】解：令阴影部分的面积是1，则：
圆面积的=×18=平行四边形面积×16=1
圆面积是：1÷18=8
平行四边形的面积是：1÷16=6
圆的面积：平行四边形的面积＝8：6＝4：3。
故选：B。
【点评】本题设出阴影部分的面积，然后根据等量关系分别求出圆的面积和平行四边形的面积，然后作比化简即可。
三．填空题
12．（白山期末）打一篇文章，小明单独完成需要15分钟，小兰单独完成需要12分钟，他们的所用时间比是　5：4　，打字速度比是　4：5　。
【分析】求两人所用时间的比，用小明的工作时间比小兰的工作时间，化简即可；
求速度比，把工作总量看作单位“1”，根据题意，小明的速度为115，小兰的速度为112，二者相比即可。
【解答】解：15：12＝5：4
115：112=4：5
答：打一篇文章，小明单独完成需要15分钟，小兰单独完成需要12分钟，他们的所用时间比是5：4，打字速度比是4：5。
故答案为：5：4，4：5。
【点评】本题考查了比的意义．解答此题用到的知识点：（1）比的意义；（2）工作总量、工作效率和工作时间三者之间的关系。
13．（白山期末）把5克糖溶解到100克水中，糖和糖水的质量比是　1：21　．
【分析】糖的质量是5克，水的质量是100克，所以糖水的质量是5+100＝105（克），糖和糖水的比为5：（5+100），化简即可．
【解答】解：5：（5+100）
＝5：105
＝1：21
答：糖和糖水的比是1：21．
故答案为：1：21．
【点评】解答此题首先应弄清：糖水的质量＝糖的质量+水的质量，这是解决本题的关．
14．（苏州期末）两个圆的半径分别是3cm和5cm，它们的周长比是　3：5　，面积比是　9：25　．
【分析】根据题意分别求出两个圆的周长和面积，然后再求比即可．
【解答】解：两个圆的周长比：（2π×3）：（2π×5）＝3：5；
两个圆的面积比：（π×32）：（π×52）＝9：25；
故答案为：3：5，9：25．
【点评】此题考查了根据半径求圆的周长比和面积比．
15．（广东期末）一种盐水，若含盐率为20%，则盐与水的比是　1：4　，盐与盐水的比是　1：5　．
【分析】把盐水的重量看作单位“1”，则水占盐水的（1﹣20%），根据题意，进行比即可．
【解答】解：20%：（1﹣20%），
＝0.2：0.8，
＝1：4；
20%：1＝1：5；
故答案为：1：4，1：5．
【点评】解答此题的关键：判断出单位“1”，进而根据题意，进行比即可．
16．（陕州区期末）小圆直径等于大圆半径的12，那么小圆面积与大圆面积的最简整数比是　1：16　．
【分析】根据题意，可设小圆的半径为r，则大圆的半径为4r，可根据圆的面积公式计算出大圆、小圆的面积，然后再用小圆的面积与大圆的面积相比，化简即可解答。
【解答】解：设小圆的半径为r，大圆的半径为4r
小圆的面积为：πr2
大圆的面积为：16πr2，
小圆的面积与大圆面积的比为：πr2：16πr2＝1：16
故答案为：1：16。
【点评】根据题意，设出小圆的半径，进而得出大圆的半径，根据圆的面积计算方法分别求出大圆和小圆的面积，是解答此题的关键。
17．（雁塔区期中）用x、y表示长方形相邻两边的长，下表是面积为36cm2的长方形相邻两边长度的变化关系．请把表格填完整，再填空．
x
1
2
3
4
6
y
36
18
12
9
6
（1）x与y成　反　比例
（2）当x＝2.5时，y＝　14.4　时，当x=13时，y＝　108　．
【分析】判断两个相关联的量之间成什么比例，就看这两个量是对应的比值一定，还是对应的乘积一定；如果是比值一定，就成正比例；如果是乘积一定，则成反比例。
【解答】解：（1）因为1×36＝36，2×18＝36，3×12＝36，4×9＝36，6×6＝36；
即x和y的乘积一定，所以x和y成反比例关系。
（2）由题意得xy＝36，
当x＝2.5时，2.5y＝36，y＝14.4
当x=13时，13y＝36，y＝108
故答案为：反，14.4，108。
【点评】此题属于辨识成正、反比例的量，就看这两个量是对应的比值一定，还是对应的乘积一定，再做判断。
．
18．（无锡）小军坐汽车去上海旅游，他每过10分钟看一次里程表上的读数，结果记录如下：
时间
8：10
8：20
8：30
8：40
8：50
……
里程表读数（km）
31220
31235
31250
？
31280
……
（1）如表所示，这辆汽车行驶的路程和时间成　正　比例．
（2）照这样的速度，8：40时里程表上的读数是　31265　．
（3）如果8：50时他们离上海还有60千米，照这样的速度，他们到达上海的时间是　9：30　．
【分析】后面一个里程表读数减相邻的前一个里程表读数就是此时间段所行驶的路程．据此即可分别求出各时间段所行驶的路程．根据时间的推算，用后一个时刻减前一个相邻时刻就是此时间段的时间．通过计算可以发现时间段相同，所行驶的路程也相同．根据“速度＝路程÷时间”，计算出这辆汽车的速度，如果速度相等，即一定，即路程÷时间＝速度（一定），则路程与时间成正比例关系．
【解答】解：（1）8：20﹣8：10＝10分
31235﹣31220＝15（km）
15÷10＝1.5（km/分）；
8：30﹣8：20＝10分
31250﹣31235＝15（km）
15÷10＝1.5（km/分）；
8：40﹣8：30＝10分
31265﹣31250＝15（km）
15÷10＝1.5（km/分）；
8：50﹣8：40＝10分
31280﹣31265＝15（km）
15÷10＝1.5（km/分）；
……
这辆汽车行驶的路程和所用时间的比值（商）一定，它们成正比例关系．

（2）60÷1.5＝40（分）
8时50分+40分＝9时30分
9时30分＝9：30
答：他们到达上海的时间是9：30．
故答案为：正，31265，9：30．
【点评】此题主要是考查了正、反比例的辨析和时间的推算．
19．（滕州市）（1）大白鲨2小时游140千米，照这样的速度，5小时游多少千米？题目中，　大白鲨游的路程　和　时间　成　正　比例关系．
（2）六年级同学做广播操，每行站20人，正好站12行．如果每行站16人，能站多少行？此题中，　站的行数　和　每行站的人数　成　反　比例关系．
【分析】判断两个相关联的量之间成什么比例，就看这两个量是对应的比值一定，还是对应的乘积一定；如果是比值一定，就成正比例；如果是乘积一定，则成反比例．
【解答】解：（1）路程÷时间＝速度（一定），比值一定，大白鲨游的路程和时间成正比例；
（2）站的行数×每行站的人数＝六年级总人数（一定），乘积一定，站的行数和每行站的人数成反比例．
故答案为：大白鲨游的路程，时间，正；站的行数，每行站的人数，反．
【点评】本题主要考查辨识成正比例的量和成反比例的量．
20．（南海区）正方形的周长和它的边长成　正　比例．
【分析】判断正方形的周长和它的边长之间成什么比例，就看这两个量是对应的比值一定，还是对应的乘积一定；如果是比值一定，就成正比例；如果是乘积一定，则成反比例．
【解答】解：因为正方形的周长＝边长×4，
所以正方形的周长÷边长＝4（一定），
即正方形的周长和它的边长的比值一定，
符合正比例的意义，所以正方形的边长和周长成正比例，
故答案为：正．
【点评】此题属于辨识成正、反比例的量，就看这两个量是对应的比值一定，还是对应的乘积一定，再做判断．
21．（沈河区）路程一定，速度与时间成　反　比例．
【分析】根据正反比例的意义，分析数量关系，找出一定的量，然后看那两个变量是比值一定还是乘积一定，从而判定成什么比例关系．
【解答】解：速度和时间是两种相关联的量，它们与路程有下面的关系：
速度×时间＝路程（一定）；
已知路程一定，也就是速度与时间的乘积一定，所以速度与时间成反比例．
故答案为：反
【点评】此题重点考查正比例和反比例的意义．
四．判断题
22．（德江县期末）北京队与江苏队场上比分为2：0，所以比的后项有时可以为0。　×　（判断对错）
【分析】比的意义是：两个数相除，又叫做两个数的比。可见，比是除法的另一种表示形式，是两个数间的关系。除数不能为0，比的后项就不能为0，否则，比无意义。北京队与江苏队场上比分为2：0，这里表示两个队比赛进球的情况，0表示没有进球，它不是数学中的比。
【解答】解：意义不同，
比的意义是：两个数相除，又叫做两个数的比，比的后项不能为零。
北京队与江苏队场上比分为2：0，这里表示两个队比赛进球的情况，0表示没有进球，它不是数学中的比。
故答案为：×．
【点评】本题考查比的意义与进球比的不同点，后者是写成比的形式，但不是数学中的比。
23．（法库县期末）淘气和笑笑比赛做口算题，淘气4分钟做32道，笑笑5分钟做35道，淘气与笑笑做题的速度比是32：35。　×　（判断对错）
【分析】首先根据工作效率＝工作量÷工作时间，分别求出两人每分钟各做多少道题；然后根据题意求比即可判断。
【解答】解：（32÷4）：（35÷5）＝8：7
所以原题说法错误。
故答案为：×。
【点评】本题主要考查了比的意义，关键是先求出俩人做题的速度，然后再进行比即可，注意要化成最简比。
24．（兴仁市校级期末）从甲地到乙地，客车用4小时，货车用6小时，客货两车的速度之比是3：2．　√　．（判断对错）
【分析】设甲乙两地的路程为1，从甲地到乙地客车要行4小时，客车的速度就是14，货车要行5小时，货车的速度就是16，客货两车的速度之比是14÷16，再化简判断即可．
【解答】解：14÷16
＝（14×12）：（16×12）
＝3：2，
故答案为：√．
【点评】本题考查了比的意义．关键是设甲乙两地的路程为1，客车的速度是14，货车的速度是16．
25．（雁塔区期中）一个孩子的身高和他的年龄成正比例．　×　（判断对错）
【分析】判断两个相关联的量之间成什么比例，就看这两个量是对应的比值一定，还是对应的乘积一定；如果是比值一定，就成正比例；如果是乘积一定，则成反比例。
【解答】解：通常在生长期，人的身高是随着年龄的增长而增长，但是生长期过了后，骨膜会闭合，停止长高；
即人的身高与年龄的比值是不一定的，
所以一个孩子的身高和他的年龄不成正比例；所以原题说法错误。
故答案为：×。
【点评】此题属于辨识成正、反比例的量，就看这两个量是对应的比值一定，还是对应的乘积一定，再做判断。
26．（温州）总亩数一定，已经播种的亩数和剩下的亩数成正比例．　×　（判断对错）
【分析】判断两个相关联的量之间成什么比例，就看这两个量是对应的比值一定，还是对应的乘积一定；如果是比值一定，就成正比例；如果是乘积一定，则成反比例．
【解答】解：已经播种的亩数+剩下的亩数＝总亩数（一定），是和一定，不符合正反比例的意义，所以已经播种的亩数和剩下的亩数不成比例；所以原题说法错误．
故答案为：×．
【点评】此题属于辨识成正、反比例的量，就看这两个量是对应的比值一定，还是对应的乘积一定，再做判断．
27.（蕲春县）一架客机从北京飞往上海，飞行速度和所用时间成反比例．　√　（判断对错）
【分析】判断两个相关联的量之间成什么比例，就看这两个量是对应的比值一定，还是对应的乘积一定；如果是比值一定，就成正比例；如果是乘积一定，则成反比例．
【解答】解：因为速度×时间＝路程（一定），是对应的乘积一定；所以速度和时间成反比例，所以原题说法正确；
故答案为：√．
【点评】此题属于辨识成正、反比例的量，就看这两个量是对应的比值一定，还是对应的乘积一定，再做判断．
五．操作题
28．（ 东海县期中）同一时间、同一地点测得的树高和它的影长如下表：
树高/米
2
3
4
6
…
影长/米
1.6
2.4
3.2
4.8
…
（1）在图中，描出表示树高和对应影长的点，然后把它们连起来．
（2）树高和影长成什么比例？为什么？
（3）量得一棵大树的影长是10.4米，这棵大树有多高？

【分析】（1）在图中找出（树高，影长）表示的点，描出表示树高和对应影长的图象即可．
（2）首先求出树高和影长的比各是多少，即可判断出树高和影长成比例，然后根据正、反比例的特征，可得树高和影长成正比例，原因是树高和影长的比值一定，据此解答即可．
（3）根据题意，用这棵树的影长乘以树高和影长的比值，求出这棵树的高度为多少米即可．
【解答】解：（1）

（2）因为2：1.6＝1.25
3：2.4＝1.25
4：3.2＝1.25
6：4.8＝1.25
因为树高和影长的比值一定，
所以树高和影长成比例，而且成正比例．
（3）10.4×1.25＝13（米）
答：这棵树的高度为13米．
【点评】此题主要考查了正、反比例应用题，要熟练掌握，解答此题的关键是要明确正比例、反比例的特征：（1）成正比例关系的这两种量中相对应的两个数的比值（即商）一定．（2）成反比例关系的这两种量中相对应的两个数的积一定