专题38 正切函数的图像和性质-2021-2022学年高一数学培优对点题组专题突破（人教A版2019必修第一册）

这是一份专题38 正切函数的图像和性质-2021-2022学年高一数学培优对点题组专题突破（人教A版2019必修第一册），文件包含专题38正切函数的图像和性质解析版docx、专题38正切函数的图像和性质原卷版docx等2份试卷配套教学资源，其中试卷共27页， 欢迎下载使用。

专题38 正切函数的图像和性质
考点1 正切函数的图像
1.如下图所示，函数y＝cosx|tanx|(0≤x＜3π2且x≠π2)的图象是(　　)
A．B．C．D．
【答案】C
【解析】∵y＝cosx|tanx|＝sinx,0≤x＜π2,-sinx,π2＜x≤πsinx,π＜x＜3π2.，
∴函数y＝cosx|tanx|(0≤x＜3π2且x≠π2)的图象是C.
2.函数y＝tanx＋sinx－|tanx－sinx|在区间π2,3π2内的图象是(　　)
A．B．C．D．
【答案】D
【解析】当π2＜x＜π时，tanx＜sinx，y＝2tanx＜0；
当x＝π时，y＝0；当π＜x＜3π2时，tanx＞sinx，y＝2sinx.故选D.
3.函数f(x)＝tanx＋1tanx，x∈x|-π2 A．B．C．D．
【答案】A
【解析】因为y＝tanx是奇函数，所以f(x)＝tanx＋1tanx，x∈x|-π2 4.函数y＝sinx与y＝tanx的图象在(－π2，π2)上的交点的个数为(　　)

A．0 B．1 C．2 D．3
【答案】B
【解析】∵sinx＜x＜tanx，x∈(0，π2)，
∴在(0，π2)上无交点，
又它们都是奇函数，故在(－π2，0)上无交点，
观察图象知两个函数的图象有1个交点.
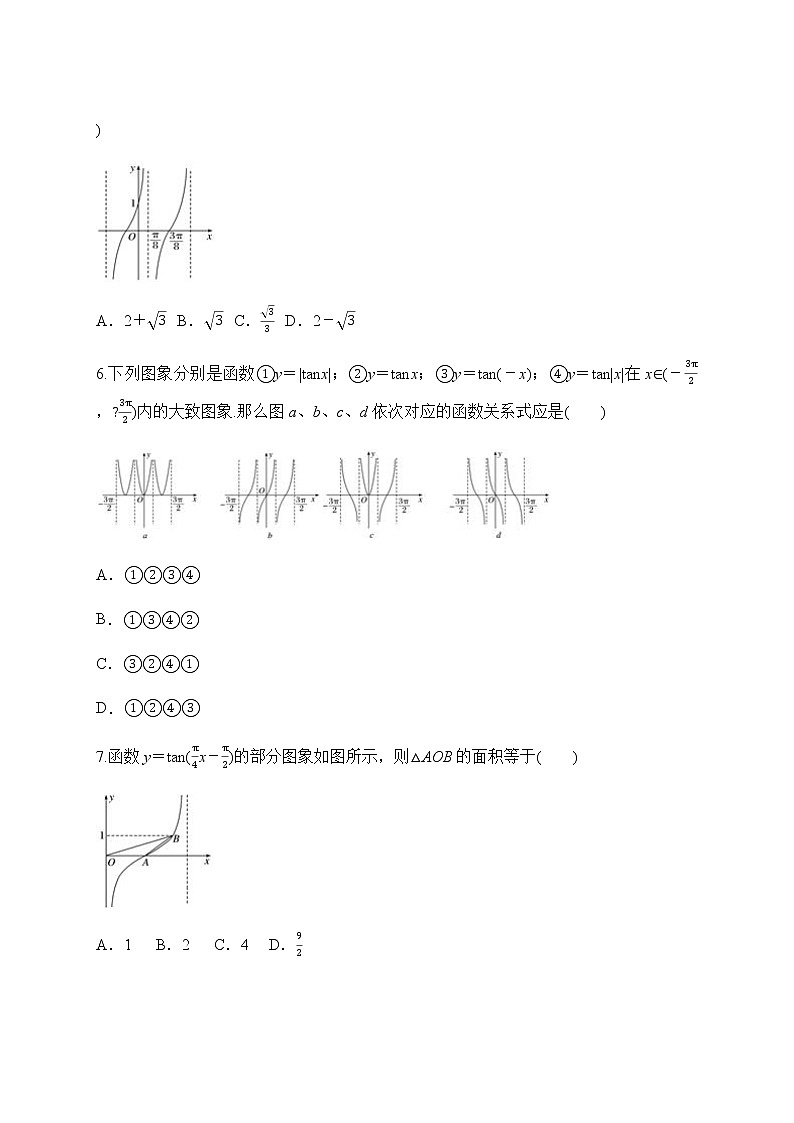
5.已知函数f(x)＝Atan(ωx＋φ)ω＞0，|φ|＜π2，y＝f(x)的部分图象如图，则f(π24)等于(　　)

A．2＋3 B．3 C．33 D．2－3
【答案】B
【解析】由图象知πω＝2×3π8-π8＝π2，ω＝2.又由于2×π8＋φ＝kπ＋π2(k∈Z)，φ＝kπ＋π4(k∈Z)，又|φ|＜π2，所以φ＝π4.这时f(x)＝Atan2x+π4.又图象过(0,1)，代入得A＝1，故f(x)＝tan2x+π4.所以fπ24＝tan2×π24+π4＝3，故选B.
6.下列图象分别是函数①y＝|tanx|；②y＝tanx；③y＝tan(－x)；④y＝tan|x|在x∈(－3π2，?3π2)内的大致图象.那么图a、b、c、d依次对应的函数关系式应是(　　)

A．①②③④
B．①③④②
C．③②④①
D．①②④③
【答案】D
【解析】y＝tan(－x)在(－π2，?π2)内是减函数，故选D.
7.函数y＝tan(π4x－π2)的部分图象如图所示，则△AOB的面积等于(　　)

A．1 B．2 C．4 D．92
【答案】A
【解析】函数的周期T＝ππ4＝4，则A(2,0)，
∴△AOB的面积S＝12×2×1＝1.
8.使不等式tanx≥3成立的x的集合为(　　)
A．(kπ＋π6，kπ＋π2)(k∈Z)
B．[kπ＋π6，kπ＋π2)(k∈Z)
C．[kπ＋π3，kπ＋π2)(k∈Z)
D．(kπ＋π3，kπ＋π2)(k∈Z)
【答案】C
【解析】∵不等式tanx≥3，
由正切函数的性质可得kπ＋π3≤x＜kπ＋π2，k∈Z，
∴使不等式成立的x的集合为{x|kπ＋π3≤x＜kπ＋π2，k∈Z}，
即x∈[kπ＋π3，kπ＋π2)(k∈Z).
考点2 正切函数的定义域、值域
9.函数y＝1tanx的定义域为(　　)
A．x|x≠0
B．x|x≠kπ，k∈Z
C．x|x≠kπ+π2，k∈Z
D．x|x≠kπ2，k∈Z
【答案】D
【解析】函数y＝1tanx有意义，则x≠kπ，k∈Z，x≠kπ+π2，k∈Z，
可得函数的定义域为x|x≠kπ2，k∈Z.
10.函数y＝sinx＋tanx的定义域为(　　)
A．x|2kπ≤x＜2kπ＋π2,k∈Z
B．x|2kπ＜x≤kπ＋π2,k∈Z
C．x|2kπ≤x＜2kπ＋π2,k∈Z∪x|x＝2kπ＋π，k∈Z
D．x|2kπ≤x＜2kπ＋π2且x≠2kπ＋π，k∈Z
【答案】C
【解析】由sinx≥0tanx≥0，即2kπ≤x≤2kπ＋πkπ≤x＜kπ＋π2(k∈Z)，得2kπ≤x＜2kπ＋π2(k∈Z)或x＝2kπ＋π(k∈Z).
所以函数y＝sinx＋tanx的定义域是x|2kπ≤x＜2kπ＋π2,k∈Z∪x|x＝2kπ＋π，k∈Z
11.函数y＝tanx-π4≤x≤π4且x≠0的值域是(　　)
A．[－1,1]
B．[－1,0)∪(0,1]
C．(－∞，1]
D．[－1，＋∞)
【答案】B
【解析】根据正切函数图象，结合函数的单调性可得.
12.函数y＝tan(sinx)的值域为(　　)
A．-π4,π4
B．-22,22
C．[－tan1，tan1]
D．以上都不对
【答案】C
【解析】∵sinx∈[－1,1]，结合函数y＝tanx的图象可知，tan(－1)≤tan(sinx)≤tan1，即
y∈[－tan1，tan1].
13.(1)求函数y＝tanx-3的定义域；
(2)已知f(x)＝tan2x－2tanx(|x|≤π3)，求f(x)的值域.
【答案】(1)要使函数有意义，必须使tanx－3≥0，即tanx≥3，
∴kπ＋π3≤x＜kπ＋π2，k∈Z.
∴函数y＝tanx-3的定义域为kπ＋π3,kπ＋+π2)(k∈Z).
(2)令u＝tanx，∵|x|≤π3，∴u∈[－3，3]，
∴函数化为y＝u2－2u.
对称轴为u＝1∈[－3，3].
∴当u＝1时，ymin＝12－2×1＝－1.
当u＝－3时，ymax＝3＋23，
∴f(x)的值域为[－1,3＋23].

考点3 正切函数的周期性和对称性
14.函数y＝tanωx的最小正周期为π2，则实数ω的值为(　　)
A．12
B．1
C．2
D．4
【答案】C
【解析】因为函数y＝tanωx的最小正周期为π2，所以π|ω|＝π2，考察选项可知，实数ω的值为2.
15.已知函数y＝tanωx(ω＞0)的图象与直线y＝a相交于A，B两点，若AB长度的最小值为π，则ω的值为(　　)
A．4
B．2
C．1
D．3
【答案】C
【解析】根据函数y＝tanωx(ω＞0)的图象特点可知，两点间的距离必是最小正周期的正整数倍，
又由两点间长度的最小值为π，即函数最小正周期为π，所以π|ω|＝π.
又由ω＞0，则ω＝1.
16.函数y＝tan35x是(　　)
A．周期为π的偶函数
B．周期为53π的奇函数
C．周期为53π的偶函数
D．周期为π的奇函数
【答案】B
【解析】正切函数的周期T＝π35＝53π，函数y＝tan35x是奇函数.
17.下列函数中，为偶函数的是(　　)
A．f(x)＝sin(2015π2＋x)
B．f(x)＝cos(2015π2＋x)
C．f(x)＝tan(2015π2＋x)
D．f(x)＝sin(2014π2＋x)
【答案】A
【解析】对于A，f(x)＝sin(2015π2＋x)＝sin(1007π＋π2＋x)＝sin(3π2＋x)＝－cosx，为偶函数，则A正确；
对于B，f(x)＝cos(2015π2＋x)＝cos(1007π＋π2＋x)＝cos(3π2＋x)＝sinx，为奇函数，则B错误；
对于C，f(x)＝tan(2015π2＋x)＝tan(1007π＋π2＋x)＝tan(π2＋x)＝－cotx，为奇函数，则C错误；
对于D，f(x)＝sin(1007π＋x)＝sin(π＋x)＝－sinx，为奇函数，故D错误.
故选A.
18.函数y＝tanx+π3图象的对称中心的坐标是(　　)
A．kπ-π3,0(k∈Z)
B．(k2π－π3，0)(k∈Z)
C．(kπ2，0)(k∈Z)
D．(kπ，0)(k∈Z)
【答案】B
【解析】函数y＝tanx+π3的图象由函数y＝tanx的图象向左平移π3个单位得到，
又由函数y＝tanx的对称中心的坐标是(kπ2，0)(k∈Z)，
∴函数y＝tan(x＋π3)的对称中心的坐标是(k2π－π3，0)(k∈Z).
19.下列坐标所表示的点不是函数y＝tan(x2－π6)的图象的对称中心的是(　　)
A．π3,0 B．-5π3,0 C．7π3,0 D．2π3,0
【答案】D
【解析】将π3，－5π3，7π3代入y＝tan(x2－π6)均为0，而2π3代入y＝tan(x2－π6)不为0，所以选D.
20.下列关于函数y＝tanx+π3的说法正确的是(　　)
A．在区间-π6+5π6上单调递增
B．最小正周期是π
C．图象关于点π4,0成中心对称
D．图象关于直线x＝π6成轴对称
【答案】B
【解析】令kπ－π2＜x＋π3＜kπ＋π2，解得kπ－5π6＜x＜kπ＋π6，k∈Z，显然-π6，5π6不满足上述关系式，故A错误；易知该函数的最小正周期为π，故B正确；令x＋π3＝kπ2，解得x＝kπ2－π3，k∈Z，任取k值不能得到x＝π4，故C错误；正切曲线没有对称轴，因此函数y＝tanx+π3的图象也没有对称轴，故D错误.故选B.
21.若函数f(x)＝2cos(4x＋π7)－1与函数g(x)＝5tan(ax－1)＋2的最小正周期相同，则实数a＝______.
【答案】±2
【解析】函数f(x)＝2cos(4x＋π7)－1的周期是π2，函数g(x)＝5tan(ax－1)＋2的最小正周期是π|a|，
因为周期相同，所以π|a|＝π2，解得a＝±2.
22.给出下列命题：
①正切函数的图象的对称中心是唯一的；
②y＝|sinx|，y＝|tanx|的周期分别为π，π2；
③若x1＞x2，则sinx1＞sinx2；
④若f(x)是R上的奇函数，它的最小正周期为T，则f(－T2)＝0.
其中正确命题的序号是________.
【答案】④
【解析】①正切函数的图象的对称中心是唯一的，由正切函数的性质可知，①是错误的；
②y＝|sinx|，y＝|tanx|的周期分别为π，π2，前者正确，后者错误，②是错误的；
③若x1＞x2，则sinx1＞sinx2，如果x1＝390°，x2＝90°，sinx1＜sinx2，③是错误的；
④若f(x)是R上的奇函数，它的最小正周期为T，则f(－T2)＝0，f(x＋T)＝f(x)，
f(－T2＋π)＝f(－T2)＝－f(T2)，f(－T2)＝0，④是正确的.
故答案为④.
23.试判断下列函数的奇偶性.
(1)f(x)＝1－2cosx＋|tanx|；
(2)f(x)＝x2tanx－sin2x.
【答案】(1)函数的定义域为{x|x≠π2＋kπ，k∈Z}，
f(－x)＝1－2cos(－x)＋|tan(－x)|＝1－2cosx＋|tanx|＝f(x)，
∴函数f(x)是偶函数.
(2)函数的定义域为{x|x≠π2＋kπ，k∈Z}，
f(－x)＝(－x)2tan(－x)－sin2(－x)＝－x2tanx－sin2x，
∴函数f(x)是非奇非偶函数.
考点4 正切函数的单调性
24.下列说法正确的是(　　)
A．y＝tanx是增函数
B．y＝tanx在第一象限是增函数
C．y＝tanx在某一区间上是减函数
D．y＝tanx在区间(kπ－π2，kπ＋π2)(k∈Z)上是增函数
【答案】D
【解析】由正切函数的图象可知D正确.
25.函数y＝tan(x＋π5)的单调递增区间是(　　)
A．-π2＋kπ，π2＋kπ(k∈Z)
B．-7π10＋kπ，3π10＋kπ(k∈Z)
C．-3π10＋kπ，7π10＋kπ(k∈Z)
D．-π5+kπ，π5＋kπ(k∈Z)
【答案】B
【解析】∵y＝tanx的单调递增区间为-π2＋kπ，π2＋kπ(k∈Z)，
令kπ－π2＜x＋π5＜kπ＋π2，解得kπ－7π10＜x＜kπ＋3π10，
∴函数y＝tan(x＋π5)的单调递增区间是-7π10＋kπ，3π10＋kπ(k∈Z).
26.关于函数f(x)＝－tan2x，有下列说法：
①f(x)的定义域是{x∈R|x≠π2＋kπ，k∈Z}；②f(x)是奇函数；③在定义域上是增函数；④在每一个区间(－π4＋kπ2，π4＋kπ2)(k∈Z)上是减函数；⑤最小正周期是π.其中正确的是(　　)
A．①②③
B．②④⑤
C．②④
D．③④⑤
【答案】C
【解析】①由正切函数的定义域可得，2x≠π2＋kπ，k∈Z，故①错误；
③由正切函数的定义域可知，函数y＝－tan2x在(－π4＋kπ2，π4＋kπ2)(k∈Z)上是减函数，故③错误；
⑤根据周期公式可得，T＝π2，故⑤错误.
27.已知函数f(x)＝3tanπxω(ω＞0).
(1)当ω＝4时，求f(x)的最小正周期及单调区间；
(2)若|f(x)|≤3在x∈[－π3，π4]上恒成立，求ω的取值范围.
【答案】(1)当ω＝4时，f(x)＝3tanπ4x，
则f(x)的最小正周期T＝ππ4＝4，由kπ－π2＜π4x＜kπ＋π2，k∈Z.
得4k－2＜x＜4k＋2，k∈Z，
即函数的单调递增区间为(4k－2,4k＋2)，k∈Z.
(2)∵ω＞0，
∴函数f(x)的周期T＝ππω＝ω，
∴若|f(x)|≤3在x∈[－π3，π4]上恒成立，
则f(x)在x∈[－π3，π4]上为单调递增函数，
满足－π3＞－12T＝－ω2，
∴ω＞2π3，∵|f(－π3)|＞f(π4)，
此时满足f(－π3)≥－3，
即f(－π3)＝3tan(－π3×πω)≥－3，
即tan(－π3×πω)≥－3，则－π3×πω≥－π3，
则πω≤1，即ω≥π，
综上，ω≥π.
考点5 正切函数的综合应用
28.对于函数y＝tanx2，下列判断正确的是(　　)
A．周期为2π的奇函数
B．周期为π2的奇函数
C．周期为π的偶函数
D．周期为2π的偶函数
【答案】A
【解析】函数y＝tanx2的周期T＝πω＝2π，再由tan(－x2)＝－tanx2可得，此函数为奇函数.
29.已知函数f(x)＝tan(2x＋π4).
(1)求该函数的定义域，周期及单调区间；
(2)若f(θ)＝17，求2cos2θ2-sinθ-12sin(θ＋π4)的值.
【答案】(1)由题意得，T＝π2.
由2x＋π4≠π2＋kπ(k∈Z)，得x≠kπ2＋π8，
由－π2＋kπ＜2x＋π4＜π2＋kπ(k∈Z)，得kπ2－3π8＜x＜kπ2＋π8，
综上得，函数的周期是π2，定义域是{x|x≠kπ2＋π8，k∈Z}，
单调增区间是(kπ2－3π8，kπ2＋π8)(k∈Z).
(2)2cos2θ2-sinθ-12sin(θ＋π4)＝cosθ－sinθsinθ＋cosθ＝1－tanθtanθ＋1，①
∵f(θ)＝17，∴tan(2θ＋π4)＝17，
则tan2θ＝tan[(2θ＋π4)－π4]＝17-11+17＝－34，
由tan2θ＝2tanθ1－tan2θ＝－34，得tanθ＝3或－13，
把tanθ＝3代入上式①得，2cos2θ2-sinθ-12sin(θ＋π4)＝－12，
把tanθ＝－13代入上式①得，2cos2θ2-sinθ-12sin(θ＋π4)＝2.
30.已知函数y＝tan(12x－π6).
(1)作出此函数在一个周期开区间上的简图；
(2)求出此函数的定义域、周期和单调区间；
(3)写出此函数图象的渐近线方程和所有对称中心的坐标.
【答案】(1)作出此函数在一个周期开区间上的简图：

则对应的图象如图：

(2)由12x－π6≠kπ＋π2，得x≠2kπ＋4π3，
即函数的定义域为{x|x≠2kπ＋4π3，k∈Z}，
函数的周期T＝π12＝2π.
由kπ－π2＜12x－π6＜kπ＋π2，k∈Z，
得2kπ－2π3＜x＜2kπ＋4π3，k∈Z，
即函数的单调递增区间为(2kπ－2π3，2kπ＋4π3)，k∈Z.
(3)由12x－π6＝kπ＋π2，得x＝2kπ＋4π3，k∈Z，
即函数图象的渐近线方程为x＝2kπ＋4π3，k∈Z，
由12x－π6＝kπ2，得x＝kπ＋π3，k∈Z.
即所有对称中心的坐标为(kπ＋π3，0).
31.已知关于实数x的不等式|x-(tanθ＋1)22|≤(tanθ-1)22，x2－3(tanθ＋1)x＋2(3tanθ＋1)≤0的解集分别为M，N，且M∩N＝∅，则这样的θ存在吗？若存在，求出θ的取值范围.
【答案】假设θ存在.由|x-(tanθ＋1)22|≤(tanθ-1)22，得2tanθ≤x≤tan2θ＋1，
∴M＝{x|2tanθ≤x≤tan2θ＋1}.∵x2－3(tanθ＋1)x＋2(3tanθ＋1)≤0，
∴当tanθ≥13时，2≤x≤3tanθ＋1.
当tanθ＜13时，3tanθ＋1≤x≤2.∵M∩N＝∅，
∴当tanθ≥13时，有3tanθ＋1＜2tanθ或tan2θ＋1＜2，
即tanθ＜－1或－1＜tanθ＜1，
∴13≤tanθ＜1.①
当tanθ＜13时，有2＜2tanθ或3tanθ＋1＞tan2θ＋1，即tanθ＞1或0＜tanθ＜3，
∴0＜tanθ＜13.②
由①②得0＜tanθ＜1，∴θ的取值范围是kπ，kπ＋π4，k∈Z.