




专题7.4坐标方法的简单应用(2)-2021-2022学年七年级数学下册同步培优题典【人教版】
展开2021-2022学年七年级数学下册尖子生同步培优题典【人教版】
专题7.4坐标方法的简单应用(2)
姓名:__________________ 班级:______________ 得分:_________________
注意事项:
本试卷满分100分,试题共24题,选择10道、填空8道、解答6道.答卷前,考生务必用0.5毫米黑色签字笔将自己的姓名、班级等信息填写在试卷规定的位置.
一、选择题(本大题共10小题,每小题3分,共30分)在每小题所给出的四个选项中,只有一项是符合题目要求的.
1.(2020春•天河区校级期中)如图,象棋盘上“将”位于点(2,﹣1),“象”位于点(4,﹣1),则“炮”位于点( )
A.(1,2) B.(2,﹣1) C.(﹣1,2) D.(2,1)
【分析】直接利用已知点坐标得出原点位置,进而得出答案.
【解析】如图所示:“炮”位于点(﹣1,2).
故选:C.
2.(2020秋•三元区期中)如图是一轰炸机群的飞行队形示意图,若在图上建立平面直角坐标,使最后两架轰炸机分别位于点M(﹣1,1)和点N(﹣1,﹣3),则第一架轰炸机位于的点P的坐标是( )
A.(﹣1,﹣3) B.(3,﹣1) C.(﹣1,3) D.(3,0)
【分析】根据M(﹣1,1)和点N(﹣1,﹣3)的坐标建立坐标系,根据坐标系解答即可.
【解析】因为M(﹣1,1)和点N(﹣1,﹣3),所以可建立如下图所示平面直角坐标系:
所以可得点P的坐标为(3,﹣1),
故选:B.
3.(2020秋•荥阳市期中)2020年9月16日,云南省瑞丽市共诊断2例新冠肺炎确诊病例,均为缅甸输入.下列表述,能确定瑞丽位置的是( )
A.云南西部
B.云南与缅甸交界处
C.东经97.85°
D.东经97.85°,北纬24.01°
【分析】根据有序数对确定坐标位置,对各选项分析判断后利用排除法求解.
【解析】A、云南西部,位置不确定,故本选项错误;
B、云南与缅甸交界处,位置不确定,故本选项错误;
C、东经97.85°,位置不明确,故本选项错误;
D、东经97.85°,北纬24.01°,有序数对,位置明确,故本选项正确.
故选:D.
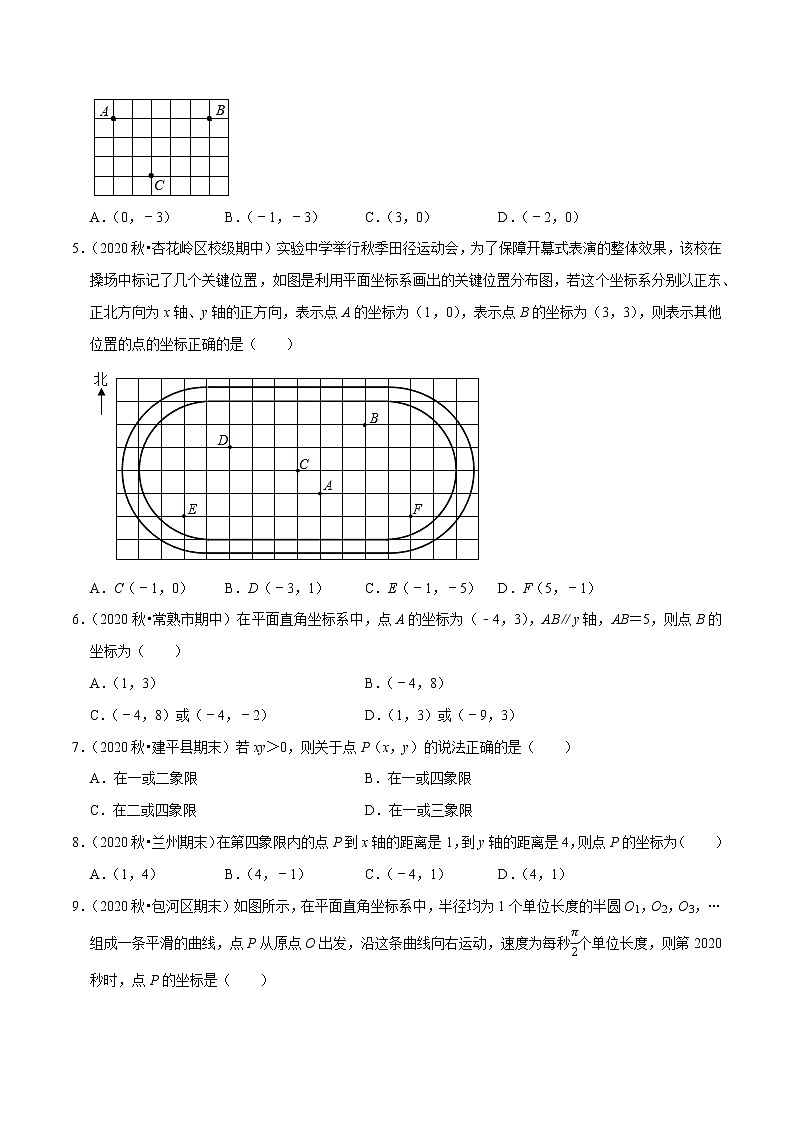
4.(2020秋•未央区期中)如图,这是一所学校的平面示意图,在同一平面直角坐标系中,教学楼A的坐标为(﹣3,0),实验楼B的坐标为(2,0),则图书馆C的坐标为( )
A.(0,﹣3) B.(﹣1,﹣3) C.(3,0) D.(﹣2,0)
【分析】直接利用已知点坐标得出原点位置,进而得出答案.
【解析】如图所示:图书馆C的坐标为(﹣1,﹣3).
故选:B.
5.(2020秋•杏花岭区校级期中)实验中学举行秋季田径运动会,为了保障开幕式表演的整体效果,该校在搡场中标记了几个关键位置,如图是利用平面坐标系画出的关键位置分布图,若这个坐标系分别以正东、正北方向为x轴、y轴的正方向,表示点A的坐标为(1,0),表示点B的坐标为(3,3),则表示其他位置的点的坐标正确的是( )
A.C(﹣1,0) B.D(﹣3,1) C.E(﹣1,﹣5) D.F(5,﹣1)
【分析】直接利用已知点坐标得出原点位置,进而得出答案.
【解析】如图所示:C(0,1),故选项A错误;
D(﹣3,2),故选项B错误;
E(﹣5,﹣1),故选项C错误;
F(5,﹣1),故选项D正确.
故选:D.
6.(2020秋•常熟市期中)在平面直角坐标系中,点A的坐标为(﹣4,3),AB∥y轴,AB=5,则点B的坐标为( )
A.(1,3) B.(﹣4,8)
C.(﹣4,8)或(﹣4,﹣2) D.(1,3)或(﹣9,3)
【分析】线段AB∥y轴,A、B两点横坐标相等,又AB=5,B点在A点上边或者下边,根据距离确定B点坐标.
【解析】∵AB∥y轴,
∴A、B两点的横坐标相同,
又AB=5,
∴B点纵坐标为:3+5=8或3﹣5=﹣2,
∴B点的坐标为:(﹣4,﹣2)或(﹣4,8);
故选:C.
7.(2020秋•建平县期末)若xy>0,则关于点P(x,y)的说法正确的是( )
A.在一或二象限 B.在一或四象限
C.在二或四象限 D.在一或三象限
【分析】根据xy>0,可得x>0,y>0或x<0,y<0,再根据各象限内点的坐标的符号特征判断即可.
【解析】∵xy>0,
∴x>0,y>0或x<0,y<0,
∴点P(x,y)在一或三象限.
故选:D.
8.(2020秋•兰州期末)在第四象限内的点P到x轴的距离是1,到y轴的距离是4,则点P的坐标为( )
A.(1,4) B.(4,﹣1) C.(﹣4,1) D.(4,1)
【分析】根据第四象限内点的横坐标是正数,纵坐标是负数,点到x轴的距离等于纵坐标的长度,到y轴的距离等于横坐标的长度求出点P的横坐标和纵坐标,然后写出答案即可.
【解析】∵点P在第四象限且到x轴的距离是1,到y轴的距离是4,
∴点P的横坐标为4,纵坐标为﹣1,
∴点P的坐标是(4,﹣1).
故选:B.
9.(2020秋•包河区期末)如图所示,在平面直角坐标系中,半径均为1个单位长度的半圆O1,O2,O3,…组成一条平滑的曲线,点P从原点O出发,沿这条曲线向右运动,速度为每秒π2个单位长度,则第2020秒时,点P的坐标是( )
A.(2019,0) B.(2020,0) C.(2019,1) D.(2020,﹣1)
【分析】计算点P走一个半圆的时间,确定第2020秒点P的位置.
【解析】点运动一个半圆用时为ππ2=2秒,
∵2020=1009×2+2,
∴2020秒时,P在第1010个的半圆的最末尾处,
∴点P坐标为(2020,0),
故选:B.
10.(2020春•天河区校级期中)如图,在平面直角坐标系中,从点P1(﹣2,0),P2(﹣2,﹣2),P3(2,﹣2),P4(2,2),P5(﹣4,2),P6(﹣4,﹣4),P7(4,﹣4),P8(4,4),P9(﹣6,4),…,依此扩展下去,则P2019的坐标为( )
A.(1010,﹣1010) B.(﹣1010,﹣1010)
C.(1010,1010) D.(﹣1012,1010)
【分析】根据各个点的位置关系,可得出下标为4的倍数的点在第一象限,被4除余1的点在第二象限,被4除余2的点在第三象限,被4除余3的点在第四象限,点P2019在第四象限,再根据第四象限点的规律即可得出结论.
【解析】由规律可得,2019÷4=504…3,
∴点P2019在第四象限,
∵点P3(2,﹣2),点P7(4,﹣4),点P11(6,﹣6),
∴点P2019(1010,﹣1010),
故选:A.
二、填空题(本大题共8小题,每小题3分,共24分)请把答案直接填写在横线上
11.(2020秋•九龙县期末)在平面直角坐标系中,点(2,3)到x轴的距离是 3 .
【分析】根据点到x轴的距离等于纵坐标的长度解答.
【解析】点(2,3)到x轴的距离是3,
故答案为:3.
12.(2020秋•道外区期末)平面直角坐标系中,点A(5,-7)到x轴的距离是 7 .
【分析】直接利用点的坐标性质得出A到x轴的距离.
【解析】∵点A(5,-7),
∴A点到x轴的距离是:7.
故答案为:7.
13.(2020秋•松北区期末)已知点P的坐标为(2﹣a,6),且点P到两坐标轴的距离相等,则a的值为 ﹣4或8 .
【分析】根据点到坐标轴的距离相等列出方程,然后求解即可.
【解析】∵点P到两坐标轴的距离相等,
∴|2﹣a|=6,
∴2﹣a=6或2﹣a=﹣6,
解得a=﹣4或a=8.
故答案为:﹣4或8.
14.(2020秋•崇明区期末)如图,在直角坐标系中,以点P为圆心的弧与x轴交于A、B两点,已知点P的坐标为(1,y),点A的坐标为(﹣1,0),那么点B的坐标为 (3,0) .
【分析】利用垂径定理,根据P点坐标,求出C点坐标,从而求出B点坐标.
【解析】∵P点坐标为(1,y),
∴C点坐标为(1,0),
∵AC=1﹣(﹣1)=2,
∴BC=AC=2,
∴OB=2+1=3,
∴B(3,0).
故答案为:(3,0).
15.(2020秋•新都区期末)如图,围棋棋盘放在某平面直角坐标系内,已知黑棋(甲)的坐标为(﹣2,2),黑棋(乙)的坐标为(﹣1,﹣2),则白棋(甲)的坐标是 (2,1) .
【分析】先利用黑棋(甲)的坐标为(﹣2,2)画出直角坐标系,然后可写出白棋(甲)的坐标.
【解析】如图,
白棋(甲)的坐标是(2,1).
故答案为(2,1).
16.(2020春•江汉区月考)已知在平面直角坐标系中,线段AB的两个端点坐标分别为A(2,5),B(6,﹣2),点P(m,n)为线段AB上一点,若平移AB使其两个端点都落在坐标轴上,则平移后点P的坐标为 (m﹣2,n+2)或(m﹣6,n﹣5) .
【分析】根据题意求得线段AB需向左平移2个单位,再向上平移两个单位或线段AB向下平移5个单位,向左平移6个单位,进而即可求平移后点P的坐标.
【解析】∵线段AB的两个端点坐标分别为A(2,5),B(6,﹣2),
∴若平移AB使其两个端点都落在坐标轴上,
∴线段AB需向左平移2个单位,再向上平移两个单位或线段AB向下平移5个单位,向左平移6个单位,
∴平移后点P的坐标为(m﹣2,n+2)或(m﹣6,n﹣5),
故答案为(m﹣2,n+2)或(m﹣6,n﹣5).
17.(2020秋•白银期末)如图,点A(0,1),点A1(2,0),点A2(3,2),点A3(5,1)…,按照这样的规律下去,点A2021的坐标为 (3032,1010). .
【分析】观察图形得到奇数点的规律为,A1(2,0),A3(5,1),A5(8,2),…,A2n﹣1(3n﹣1,n﹣1),由2019是奇数,且2021=2n﹣1,则可求A2n﹣1(3043,1012).
【解析】观察图形可得,A1(2,0),A3(5,1),A5(8,2),…,A2n﹣1(3n﹣1,n﹣1),
A2(3,2),A4(6,3),A6(9,4),…,A2n(3n,n+1),
∵2021是奇数,且2021=2n﹣1,
∴n=1011,
∴A2n﹣1(3032,1010),
故答案为(3032,1010).
18.(2020秋•抚顺县期末)如图,在平面直角坐标系中,点A1是以原点O为圆心,半径为2的圆与过点(0,﹣1)且平行于x轴的直线l1的一个交点;点A2是以原点O为圆心,半径为3的圆与过点(0,﹣2)且平行于x轴的直线l2的一个交点;…按照这样的规律进行下去,点An的横坐标为 2n+1 .
【分析】连OA1,OA2,OA3,根据题意得到OM=1,OA1=2,ON=2,OA2=3,OQ=3,OA3=4,根据勾股定理分别计算出A1M,A2N,A3Q,然后分别表示A1,A2,A3的坐标,它们的纵坐标与子母的脚标一致,而横坐标为相邻两整数差的算术平方根,其中较小的整数为此子母得脚标,按照此规律可得点An的横坐标.
【解析】连OA1,OA2,OA3,如图,
在Rt△OMA1中,OM=1,OA1=2,
∴A1M=OA12-OM2=22-12,
∴A1的横坐标为22-12;
在Rt△ONA2中,ON=2,OA2=3,
∴A2N=32-22,
∴A2的横坐标为32-22;
在Rt△ONA3中,OQ=3,OA3=4,
∴A3Q=42-32,
∴A3的横坐标为42-32;
按照此规律可得点An的横坐标为(n+1)2-n2=2n+1.
故答案为:2n+1.
三、解答题(本大题共6小题,共46分.解答时应写出文字说明、证明过程或演算步骤)
19.(2020秋•白银期末)小明和爸爸、妈妈到白银水川湿地公园游玩,回到家后,他利用平面直角坐标系画出了公园的景区地图,如图所示.可是他忘记了在图中标出原点、x轴及y轴.只知道长廊E的坐标为(4,﹣3)和农家乐B的坐标为(﹣5,3),请你帮他画出平面直角坐标系,并写出其他各点的坐标.
【分析】由长廊E的坐标为(4,﹣3)和农家乐B的坐标为(﹣5,3),可以确定平面直角坐标系中原点的位置,以及坐标轴的位置,从而可以确定其它点的坐标.
【解析】由题意可知,本题是以点D为坐标原点(0,0),DA为y轴的正半轴,建立平面直角坐标系.
则A、C、F的坐标分别为:A(0,4);C(﹣3,2);F(5,5).
20.(2020春•江汉区月考)如图,三角形A′B′C′是由三角形ABC经过某种平移得到的,点A与点A′,点B与点B′,点C与点C′分别对应,且这六个点都在格点上,观察各点以及各点坐标之间的关系,解答下列问题:
(1)分别写出点B和点B′的坐标,并说明三角形A′B′C′是由三角形ABC经过怎样的平移得到的;
(2)连接BC′,直接写出∠CBC′与∠B′C′O之间的数量关系 ∠CBC′﹣∠B′C′O=90° ;
(3)若点M(a﹣1,2b﹣5)是三角形ABC内一点,它随三角形ABC按(1)中方式平移后得到的对应点为点N(2a﹣7,4﹣b),求a和b的值.
【分析】(1)由图形可得出点的坐标和平移方向及距离;
(2)根据平移的性质和平角的定义和平行线的性质即可求解;
(3)根据以上所得平移方式,利用“横坐标,右移加,左移减;纵坐标,上移加,下移减”的规律列出关于a、b的方程,解之求得a、b的值.
【解析】(1)由图知,B(2,1),B′(﹣1,﹣2),
三角形A′B′C′是由三角形ABC向左平移3个单位,向下平移3个单位得到的;
(2)∠CBC′与∠B′C′O之间的数量关系∠CBC′﹣∠B′C′O=90°.
故答案为:∠CBC′﹣∠B′C′O=90°;
(3)由(1)中的平移变换得a﹣1﹣3=2a﹣7,2b﹣5﹣3=4﹣b,
解得a=3,b=4.
故a的值是3,b的值是4.
21.(2020秋•龙岗区校级期中)图中标明了小强家附近的一些地方.
(1)写出公园、游艺场和学校的坐标;
(2)早晨,小强从家里出发,沿(﹣3,﹣1),(﹣1,﹣2),(0,﹣1),(2,﹣2),(1,0),(1,3),(﹣1,2)路线转了一下,又回到家里,写出他路上经过的地方.
【分析】(1)直接利用平面直角坐标系得出对应点坐标;
(2)直接利用已知点坐标得出对应位置即可.
【解析】(1)公园(3,﹣1),游艺场(3,2),学校(1,3);
(2)邮局﹣﹣移动通讯﹣﹣幼儿园﹣﹣消防队﹣﹣火车站﹣﹣学校﹣﹣糖果店.
22.(2020秋•拱墅区期中)已知当m,n都是实数.且满足2m=8+n时,称p(m﹣1,n+22)为“开心点”.
(1)判断点A(5,3),B(4,10)是否为“开心点”,并说明理由;
(2)若点M(a,2a﹣1)是“开心点”,请判断点M在第几象限?并说明理由.
【分析】(1)根据A、B点坐标,代入(m﹣1,n+22)中,求出m和n的值,然后代入2m=8+n检验等号是否成立即可;
(2)直接利用“开心点”的定义得出a的值进而得出答案.
【解析】(1)点A(5,3)为“开心点”,理由如下,
当A(5,3)时,m﹣1=5,n+22=3,得m=6,n=4,
则2m=12,8+n=12,
所以2m=8+n,
所以A(5,3)是“开心点”;
点B(4,10)不是“开心点”,理由如下,
当B(4,10)时,m﹣1=4,n+22=10,得m=5,n=18,
则2m=10,8+18=26,
所以2m≠8+n,
所以点B(4,10)不是“开心点”;
(2)点M在第三象限,
理由如下:
∵点M(a,2a﹣1)是“开心点”,
∴m﹣1=a,n+22=2a-1,
∴m=a+1,n=4a﹣4,
代入2m=8+n有2a+2=8+4a﹣4,
∴a=﹣1,2a﹣1=﹣3,
∴M(﹣1,﹣3),
故点M在第三象限.
23.(2020春•船营区期末)在平面直角坐标系中,一只蜗牛从原点O出发,按向上、向右、向下、向右的方向依次不断移动,每次移动1个单位长度,其行走路线如图所示:
(1)填写下列各点的坐标:A5( 2 , 1 ),A9( 4 , 1 ),A13( 6 , 1 );
(2)写出点A4n+1的坐标(n是正整数);
(3)指出蜗牛从点A2020到点A2021的移动方向.
【分析】(1)根据点的坐标变化即可填写各点的坐标;
(2)根据(1)发现规律即可写出点A4n+1的坐标(n为正整数);
(3)根据(2)发现的规律,每四个点一个循环,进而可得蚂蚁从点A2020到点A2021的移动方向.
【解析】(1)根据点的坐标变化可知:
各点的坐标为:A5(2,1),A9(4,1),A13(6,1);
故答案为:2,1,4,1,6,1;
②根据(1)发现:
点A4n+1的坐标(n为正整数)为(2n,1);
③因为每四个点一个循环,
所以2021÷4=505…1.
所以蚂蚁从点A2020到点A2021的移动方向是向上.
24.(2020春•新丰县期中)如图,在平面直角坐标系中,一动点从原点O出发,沿着箭头所示方向,每次移动1个单位,依次得到点P1(0,1),P2(1,1),P3(1,0),P4(1,﹣1),P5(2,﹣1),P6(2,0)…
(1)填写下列各点的坐标:P9( 3 、0 ),P12( 4 、 0 ),P15( 5 、 0 )
(2)写出点P3n的坐标(n是正整数);
(3)点P60的坐标是( 20 、 0 );
(4)指出动点从点P210到点P211的移动方向.
【分析】由题意可以知道,动点运动的速度是每次运动一个单位长度,(0,1)→(1,1)→(1,0)→(1,﹣1)……通过观察找到有规律的特殊点,如P3、P6、P9、P12,发现其中规律是脚标是3的倍数的点,依次排列在x轴上,且相距1个单位,明确这个规律即可解决以上所有问题.
【解析】(1)由动点运动方向与长度可得P3(1,0),P6(2,0),
可以发现脚标是3的倍数的点,依次排列在x轴上,且相距1个单位,
即动点运动三次与横轴相交,
故答案为P9( 3,0),P12(4、0 ),P15(5、0 ).
(2)由(1)可归纳总结点P3n的坐标为P3n(n,0),(n是正整数);
(3)根据(2),∵60=3×20,∴点P60的横坐标是20
故点P60的坐标是(20、0 )
故答案为(20、0 ).
(4)∵210=3×70,符合(2)中的规律
∴点P210在x轴上,
又由图象规律可以发现当动点在x 轴上时,偶数点向上运动,奇数点向下运动,
而点P210是在x轴上的偶数点
所以动点从点P210到点P211的移动方向应该是向上.
人教版七年级下册7.2.2用坐标表示平移课后复习题: 这是一份人教版七年级下册7.2.2用坐标表示平移课后复习题,文件包含7年级数学下册讲义同步培优题典专题74坐标方法的简单应用2教师版docx、7年级数学下册讲义同步培优题典专题74坐标方法的简单应用2学生版docx等2份试卷配套教学资源,其中试卷共23页, 欢迎下载使用。
初中数学人教版七年级下册7.2.1用坐标表示地理位置课时练习: 这是一份初中数学人教版七年级下册7.2.1用坐标表示地理位置课时练习,文件包含7年级数学下册讲义同步培优题典专题73坐标方法的简单应用1教师版docx、7年级数学下册讲义同步培优题典专题73坐标方法的简单应用1学生版docx等2份试卷配套教学资源,其中试卷共20页, 欢迎下载使用。
专题10.2直方图-2021-2022学年七年级数学下册同步培优题典【人教版】: 这是一份专题10.2直方图-2021-2022学年七年级数学下册同步培优题典【人教版】,文件包含专题102直方图-2021-2022学年七年级数学下册尖子生同步培优题典解析版人教版docx、专题102直方图-2021-2022学年七年级数学下册尖子生同步培优题典原卷版人教版docx等2份试卷配套教学资源,其中试卷共25页, 欢迎下载使用。












