





高中数学人教A版 (2019)必修 第二册9.1 随机抽样评课ppt课件
展开普查:对每一个调查对象都进行调查的方法,称为全面调查(verall survey),又称普查.在一个调查中,我们把调查对象的全体称为总体(ppulatin),组成总体的每一个调查对象称为个体(individual).抽样调查:根据一定目的,从总体中抽取一部分个体进行调查,并以此为依据对总体的情况作出估计和推断的调查方法,称为抽样调查(sampling survey).我们把从总体中抽取的那部分个体称为样本(sample),样本中包含的个体数称为样本量.调查样本获得的变量值称为样本的观测数据,简称样本数据.
抽样调查由于只抽取一部分个体进行调查,因此具有花费少、效率高的特点.在总体规模比较大的调查中,如果经费、时间上受限,那么抽样调查是比较合适的调查方法.还有一些调查是毁损性的,也只能用抽样调查.
二、 普查和抽样调查的对比
我们生活在一个数字化时代,时刻都在和数据打交道,例如,产品的合格率,农作物的产量,商品的销售量,电视台的收视率等.
统计的研究对象是数据,核心是通过数据分析研究和解决问题,因此,首先要设法获取与问题有关的数据,从而为解决问题奠定基础.
些数据常常是通过抽样调查或全面调查而获得的,如何从总体中抽取具有代表性的样本,是我们需要研究的课题.
抽样调查的应用范围越来越广泛,下面我们研究两种基本的抽样方法——简单随机抽样和分层随机抽样
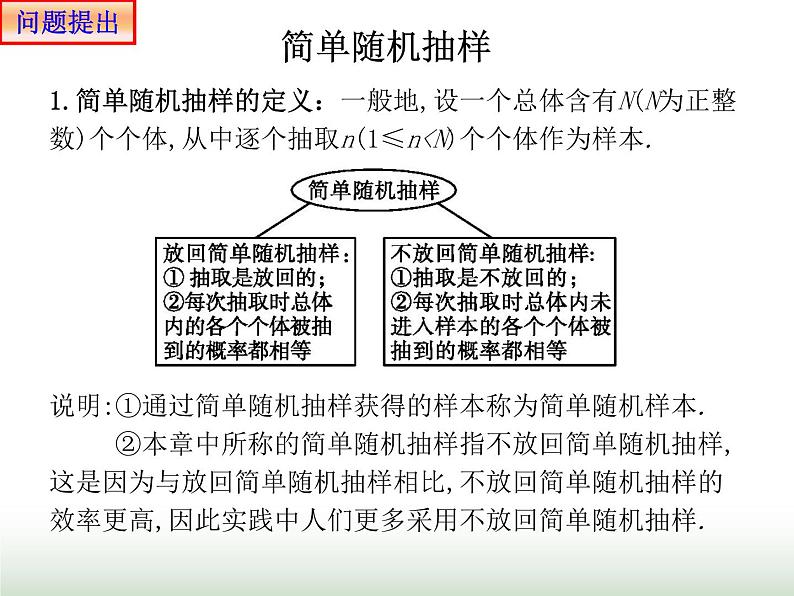
1.简单随机抽样的定义:一般地,设一个总体含有N(N为正整数)个个体,从中逐个抽取n(1≤n
下列5个抽样中,简单随机抽样的个数是( )①从无数个个体中抽取50个个体作为样本;②仓库中有1万支奥运火炬,从中一次性抽取100支火炬进行质量检查;③一彩民选号,从装有36个大小、形状都相同的号签的盒子中无放回地逐个抽出6个号签;④箱子里共有100个零件,从中选出10个零件进行质量检验,在抽样操作中,从中任意取出1个零件进行质量检验后,再把它放回箱子里.A.0B.1C.2D.3
解析:根据简单随机抽样的特点逐个判断.①不是简单随机抽样.因为简单随机抽样要求被抽取的总体的个数是有限的.②不是简单随机抽样.虽然“一次性抽取”和“逐个抽取”不影响个体被抽到的可能性,但简单随机抽样要求的是“逐个抽取”.③是简单随机抽样.因为总体中的个体数是有限的,并且是从总体中逐个进行抽取的,是等可能的抽样.④是简单随机抽样,因为它是放回简单随机抽样.综上,只有③④是简单随机抽样.
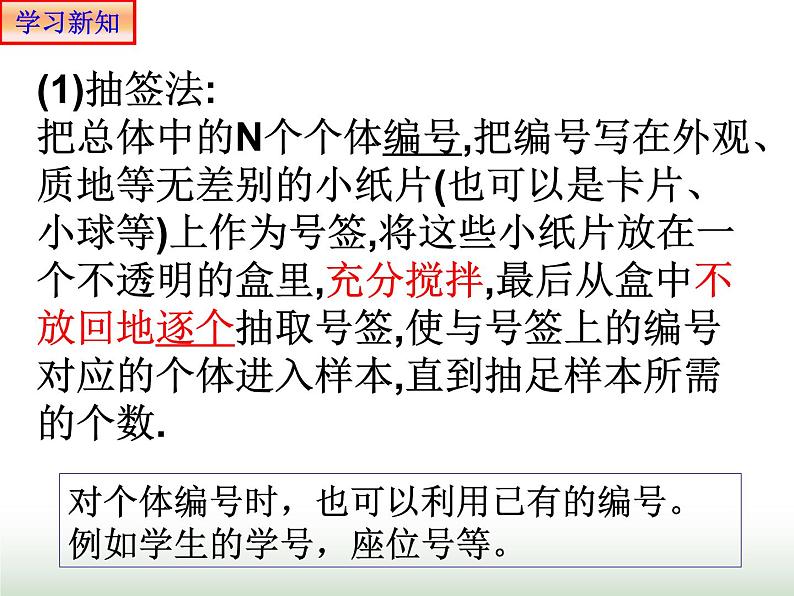
(1)抽签法:把总体中的N个个体编号,把编号写在外观、质地等无差别的小纸片(也可以是卡片、小球等)上作为号签,将这些小纸片放在一个不透明的盒里,充分搅拌,最后从盒中不放回地逐个抽取号签,使与号签上的编号对应的个体进入样本,直到抽足样本所需的个数.
对个体编号时,也可以利用已有的编号。例如学生的学号,座位号等。
提示: (1)给个体编号时可利用已有编号,如学号、考号、标签号等;(2)制作号签时,所使用的工具(如纸条、小球等)形状、大小应当都一样,以确保每个号签被抽到的可能性相等;(3)在抽签法中,搅拌均匀的目的是让每个号签被抽到的机会均等.
1.抽签法的操作步骤:第一步,编号:将N个个体编号(号码可以从1到N,也可以使用已有的号码).第二步,写签:将N个号码写到大小、形状相同的号签上.第三步,抽签:将号签搅拌均匀,每次从中抽取一个号签,连续不放回地抽取n次,并记录其编号.第四步,定样:从总体中找出与号签上的号码对应的个体,组成样本.
2.思考:抽签法有什么优点和缺点?
(1)优点:简单易行,当总体的个体数不多时,使总体处于“搅拌”均匀的状态比较容易,这时,每个个体都有均等的机会被抽中,从而能够保证样本的代表性.(2)缺点:仅适用于个体数较少的总体,当总体容量较大时,费时费力又不方便,况且,如果号签搅拌的不均匀,可能导致抽样不公平.
例1.某大学为了支援西部教育事业,现从报名的18名志愿者中选取6人组成志愿小组,请用抽签法确定志愿小组成员,并写出抽样步骤.
分析编号→制签→搅匀→抽签→成样解:抽样步骤是:第一步,将18名志愿者编号,号码是01,02,…,18.第二步,将号码分别写在同样的小纸片上,揉成团,制成号签.第三步,将得到的号签放入一个不透明的袋子中,并充分搅匀.第四步,从袋子中依次抽取6个号签,并记录上面的编号.第五步,与所得号码对应的志愿者就是志愿小组的成员.
利用抽签法抽取样本时应注意的问题(1)编号时,如果已有编号(如学号,标号等),那么可不必重新编号.(2)号签要求大小、形状完全相同.(3)号签要搅拌均匀.(4)要逐一不放回地抽取.
2.随机数法(1)定义:先把总体中的个体编号,用随机数工具产生与总体中个体数量相等的整数随机数,把产生的随机数作为抽中的编号,并剔除重复的编号,直到抽足样本所需要的个体数.(2)产生随机数的方法:①用随机试验生成随机数,②用信息技术生成随机数:计算器、电子表格、R软件等
随机数法的步骤(1)先给N个个数编号,例如按1~N进行编号;(2)用随机数工具产生1~N范围内的整数随机数;(3)把产生的随机数作为抽中的编号,使与编号对应的个体进入样本;(4)重复上述过程,直到抽足样本所需要的个体数.
2、用随机数表法进行抽取
(1)随机数表是统计工作者用计算机生成的随机数,并保证表中的每个位置上的数字是等可能出现的。
(3)用随机数表抽取样本,可以任选一个数作为开始,读数的方向可以向左,也可以向右、向上、向下等等。因此并不是唯一的.
(2)用随机数表进行抽样的步骤:将总体中个体编号;选定开始的数字;获取样本号码。
(4)由于随机数表是等机会的,因此利用随机数表抽取样本保证了被抽取个体的机会是相等的。
例 为了检验某种产品的质量,决定从40件产品中抽取10件进行检查,试用随机数表法抽取一组样本.
第一步,先将40件产品编号,可以编为00,01,02,……,38,39.
第二步,在随机数表课本103页中任选一个数作为开始.
第三步,从选定的数(如第8行第17列的数67)开始向右读下去,得到一个两位数字号码19,由于19<39,将它取出;继续向右读,得到98,将它去掉;继续读下去,又得到10,12,07,39,38,33,21,随后的两位数字号码是12,由于它在前面已经取出,将它去掉,再继续下去,得到34,29
至此,10个样本号码已经取满,于是,所要抽取的样本号码是 19 10 12 07 39 38 33 21 34,29
例: 现有120台机器,请用随机数法抽取10台机器,写出抽样过程.
【分析】 已知N=120,n=10,用随机数法抽样时编号000,001,002,…,119,抽取10个编号(都是三位数),对应的机器组成样本.
【解】第一步,先将120台机器编号,可以编为000,001,002,…,119;第二步,利用工具(转盘、科学计算器或计算机等)产生000,001,002,…,119中的随机数,产生的数是几,就选第几号个体;第三步,重复第二步,若生成的随机数重复,则剔除重复的编号并重新产生随机数,凡不在000~119中的数跳过去不取,直至选到预先设定的样本容量.
(1)总体均值:一般地,总体中有N个个体,它们的变量值分别为Y1,Y2,…,YN,则 为总体均值,又称总体平均数.
(2)总体均值加权平均数的形式:如果总体的N个变量值中,不同的值共有k(k≤N)个,不妨记为Y1,Y2,…,Yk,其中Yi出现的频数fi(i=1,2,…,k),则总体均值还可以写成加权平均数的形式__________.
【例】 某市质监局要检查某公司某个时间段生产的500克袋装牛奶的质量是否达标,现从500袋牛奶中抽取10袋进行检验,(1)利用随机数法抽取样本时,应如何操作?(2)如果用随机试验生成部分随机数如下所示,从第一个数开始抽取,据此写出应抽取的袋装牛奶的编号.
解:(1)第一步,将500袋牛奶编号为001,002.….500.第二步,用随机数工具产生1~500范围内的随机数.第三步,把产生的随机数作为抽中的编号,使编号对应的袋装牛奶进入样本.第四步,重复上述过程,直到产生不同的编号等于样本所需要的数量.
(2)应抽取的袋装牛奶的编号为:162,277,354,384,263,491,175,331,455,068.
(3)质监局对该公司生产的袋装牛奶检验的质量指标有两个:一是每袋牛奶的质量满足500±5g,二是10袋质量的平均数≥500g,同时满足这两个指标,才认为公司生产的牛奶为合格,否则为不合格.经过检测得到10袋袋装牛奶的质量(单位:g)为:502,500,499,497,503,499,501,500,498,499.计算这个样本的平均数,并按照以上标准判断牛奶质量是否合格.
变式1.该公司对质监部门的这种检验方法并不认可,公司自己质检部门抽取了100袋牛奶按照本例(3)检验标准,统计得到这100袋袋装牛奶的质量都满足500±5g,平均数为500.4g,你认为质监局和公司的检验结果哪一个更可靠?为什么?
[解] 该公司的质检部门的检验结果更可靠.因为质监局抽取的样本较少,不能很好地反映总体,该公司的质检部门抽取的样本量较大,一般来说,样本量大的会好于样本量小的.尤其是样本量不大时,增加样本量可以较好地提高估计的效果.
4.某大学要去贫困地区参加支教活动,需要从每班选10名男生,8名女生参加,某班有男生32名,女生28名,试用抽签法确定该班参加支教活动的同学.
3.在总体为N的一批零件中抽取一个容量为30的样本,若每个零件被抽取的可能性为25%,则N的值为 .
6.在简单随机抽样中,某一个体被抽到的可能性( )A.与第几次抽样有关,第一次抽到的可能性大一些B.与第几次抽样无关,每次抽到的可能性都相等C.与第几次抽样有关,最后一次抽到的可能性要大一些D.与第几次抽样无关,每次都是等可能的抽取,且各次抽取的可能性不同
5.使用简单随机抽样从1000件产品中抽出50件进行某项检查,合适的抽样方法是( )A.抽签法 B.随机数法 C.随机抽样法 D.以上都不对
7.下面抽样方法是简单随机抽样的是( )A.从平面直角坐标系中抽取5个点作为样本B.可口可乐公司从仓库中的1 000箱可乐中一次性抽取20箱进行质量检查C.某连队从200名战士中,挑选出50名最优秀的战士去参加抢险救灾活动D.从10个手机中逐个不放回地随机抽取2个进行质量检验(假设10个手机已编好号,对编号随机抽取)
8.用抽签法抽取的一个容量为5的样本,它们的变量值分别为2,4,5,7,9,则该样本的平均数为( )A.4.5 B.4.8 C.5.4 D.6
9.为迎接2022年北京冬奥会,奥委会现从报名的某高校30名志愿者中选取6人组成奥运志愿小组,请用抽签法设计抽样方案.
[解] (1)将30名志愿者编号,号码分别是01,02,…,30;(2)将号码分别写在外观、质地等无差别的小纸片上作为号签.(3)将小纸片放入一个不透明的盒里,充分搅匀.(4)从盒中不放回地逐个抽取6个号签,使与号签上编号相同的志愿者进入样本.
10.某工厂的质检人员采用随机数法对生产的100件产品进行检查,若抽取10件进行检查,应如何对100件产品编号?
可对这100件产品编号为:00,02,03,…,99.
1.要判断所给的抽样方法是不是简单随机抽样,关键是看它们是否符合简单随机抽样的定义,即简单随机抽样的四个特点:总体有限、逐个抽取、无放回抽取、等可能抽取.2.一个抽样试验能否用抽签法,关键看总体和样本的容量是否较少.
随机数法的注意点(1)当总体容量较大,样本容量不大时,可用随机数法抽取样本.(2)用随机数法抽取样本,为了方便,在编号时需统一编号的位数.(3) 掌握利用信息技术产生随机数的方法和规则.
人教A版 (2019)必修 第二册9.1 随机抽样精品ppt课件: 这是一份人教A版 (2019)必修 第二册9.1 随机抽样精品ppt课件,共1页。
人教A版 (2019)必修 第二册9.1 随机抽样示范课课件ppt: 这是一份人教A版 (2019)必修 第二册9.1 随机抽样示范课课件ppt,文件包含第1课时简单随机抽样的概念及常用方法pptx、第2课时总体均值和样本均值pptx、第1课时分层演练综合提升docx、第2课时分层演练综合提升docx等4份课件配套教学资源,其中PPT共52页, 欢迎下载使用。
高中数学人教A版 (2019)必修 第二册第九章 统计9.1 随机抽样课堂教学课件ppt: 这是一份高中数学人教A版 (2019)必修 第二册第九章 统计9.1 随机抽样课堂教学课件ppt,共30页。













