

























中考数学总复习 08第八章 专题拓展 PPT课件(福建专用)
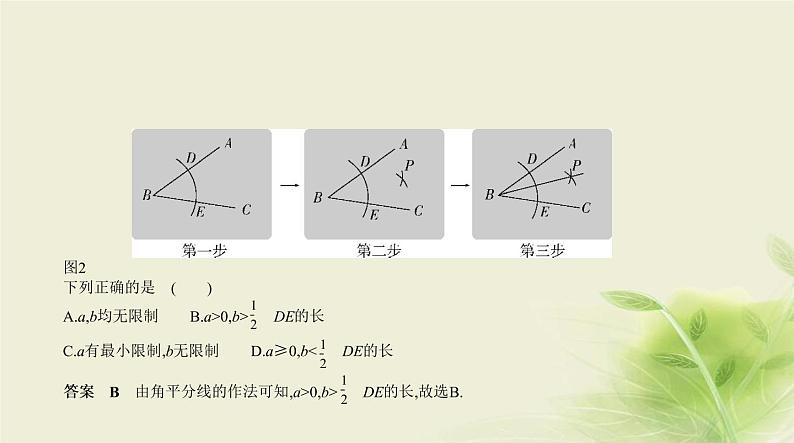
展开1.(2020河北,6,3分)如图1,已知∠ABC,用尺规作它的角平分线.如图2,步骤如下,第一步:以B为圆心,以a为半径画弧,分别交射线BA,BC于点D,E;第二步:分别以D,E为圆心,以b为半径画弧,两弧在∠ABC内部交于点P;第三步:画射线BP.射线BP即为所求. 图1
图2下列正确的是 ( )A.a,b均无限制 B.a>0,b> DE的长C.a有最小限制,b无限制 D.a≥0,b< DE的长
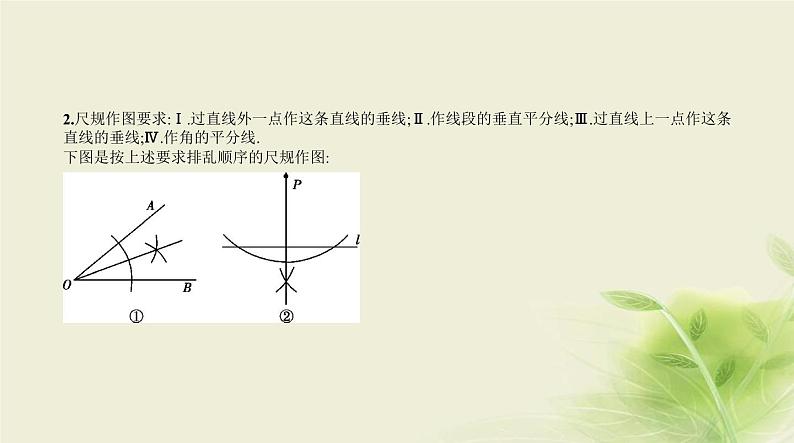
2.尺规作图要求:Ⅰ.过直线外一点作这条直线的垂线;Ⅱ.作线段的垂直平分线;Ⅲ.过直线上一点作这条 直线的垂线;Ⅳ.作角的平分线.下图是按上述要求排乱顺序的尺规作图:
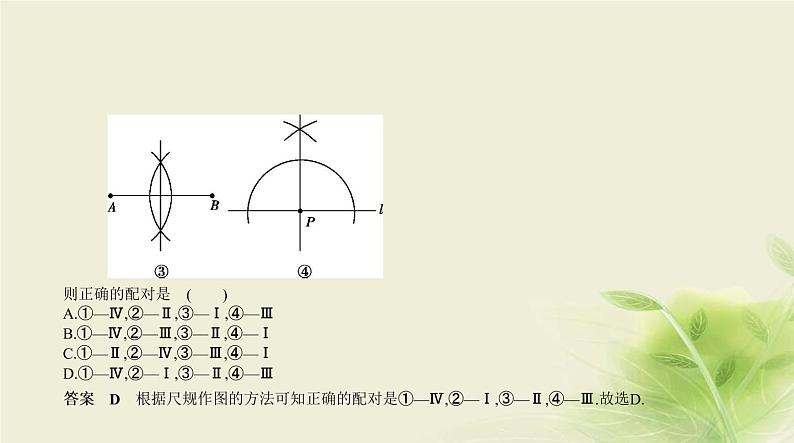
则正确的配对是 ( )A.①—Ⅳ,②—Ⅱ,③—Ⅰ,④—ⅢB.①—Ⅳ,②—Ⅲ,③—Ⅱ,④—ⅠC.①—Ⅱ,②—Ⅳ,③—Ⅲ,④—ⅠD.①—Ⅳ,②—Ⅰ,③—Ⅱ,④—Ⅲ
答案 D 根据尺规作图的方法可知正确的配对是①—Ⅳ,②—Ⅰ,③—Ⅱ,④—Ⅲ.故选D.
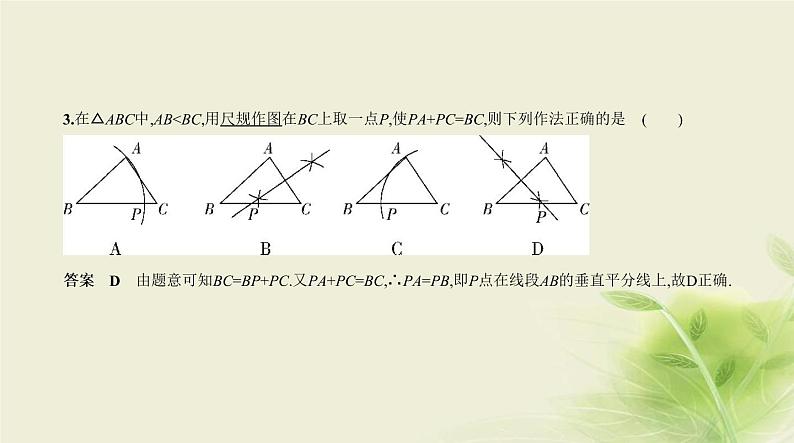
3.在△ABC中,AB
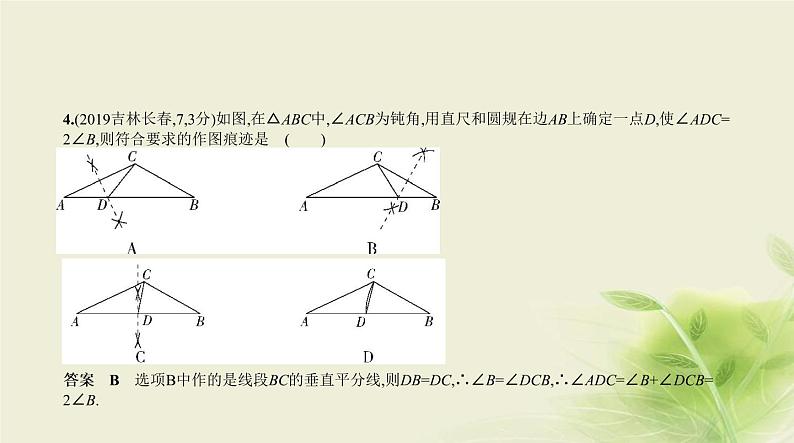
4.(2019吉林长春,7,3分)如图,在△ABC中,∠ACB为钝角,用直尺和圆规在边AB上确定一点D,使∠ADC=2∠B,则符合要求的作图痕迹是 ( )
答案 B 选项B中作的是线段BC的垂直平分线,则DB=DC,∴∠B=∠DCB,∴∠ADC=∠B+∠DCB=2∠B.
思路分析 利用线段垂直平分线上的点到线段两个端点的距离相等,找出与∠B相等的角,利用三角形 外角与内角的关系分析.
5.(2018山西,14,3分)如图,直线MN∥PQ,直线AB分别与MN,PQ相交于点A,B.小宇同学利用尺规按以下步 骤作图:①以点A为圆心,以任意长为半径作弧交AN于点C,交AB于点D;②分别以C,D为圆心,大于 CD长为半径作弧,两弧在∠NAB内交于点E;③作射线AE交PQ于点F.若AB=2,∠ABP=60°,则线段AF的长为 .
解析 过点B作BG⊥AF交AF于点G, 由尺规作图可知,AF平分∠NAB,∴∠NAF=∠BAF.∵MN∥PQ,∴∠NAF=∠BFA,∴∠BAF=∠BFA,∴BA=BF=2.∵BG⊥AF,∴AG=FG,∵∠ABP=60°,∴∠BAF=∠BFA=30°.在Rt△BFG中,FG=BFcs∠BFG=2× = ,∴AF=2FG=2 .
6.(2020北京,20,5分)已知:如图,△ABC为锐角三角形,AB=AC,CD∥AB.
求作:线段BP,使得点P在直线CD上,且∠ABP= ∠BAC.作法:①以点A为圆心,AC长为半径画圆,交直线CD于C,P两点;②连接BP.线段BP就是所求作的线段.(1)使用直尺和圆规,依作法补全图形(保留作图痕迹);(2)完成下面的证明.
证明:∵CD∥AB,∴∠ABP= .∵AB=AC,∴点B在☉A上.又∵点C,P都在☉A上,∴∠BPC= ∠BAC( )(填推理的依据).∴∠ABP= ∠BAC.
解析 (1)补全的图形如图所示. (2分)(2)∠BPC; (3分)一条弧所对的圆周角等于它所对的圆心角的一半. (5分)
7.(2018北京,17,5分)下面是小东设计的“过直线外一点作这条直线的平行线”的尺规作图过程.已知:直线l及直线l外一点P. 求作:直线PQ,使得PQ∥l.作法:如图,
①在直线l上取一点A,作射线PA,以点A为圆心,AP长为半径画弧,交PA的延长线于点B;②在直线l上取一点C(不与点A重合),作射线BC,以点C为圆心,CB长为半径画弧,交BC的延长线于点Q;③作直线PQ.所以直线PQ就是所求作的直线.根据小东设计的尺规作图过程,(1)使用直尺和圆规,补全图形;(保留作图痕迹)(2)完成下面的证明.证明:∵AB= ,CB= ,∴PQ∥l( )(填推理的依据).
解析 (1)补全图形,如图所示: (2)AP;CQ;三角形的中位线平行于三角形的第三边.
8.(2018泉州质检,19)如图,在锐角△ABC中,AB=2 cm,AC=3 cm.(1)尺规作图:作BC边的垂直平分线分别交AC,BC于点D、E(保留作图痕迹,不要求写作法);(2)在(1)的条件下,连接BD,求△ABD的周长.
解析 (1)如图所示,直线DE为所求作的直线. (2)∵DE垂直平分BC,∴BD=CD.∴△ABD的周长=AB+AD+BD=AB+AD+CD=AB+AC=5 cm.
9.如图,已知∠MAN,点B在射线AM上.(1)尺规作图(保留作图痕迹,不写作法):①在AN上取一点C,使BC=BA;②作∠MBC的平分线BD;(2)在(1)的条件下,求证:BD∥AN.
解析 (1)①②如图. (2)证明:∵AB=BC,∴∠A=∠BCA,∵BD平分∠MBC,∴∠MBD=∠CBD,∵∠MBC=∠A+∠BCA,即∠MBD+∠CBD=∠A+∠BCA,∴∠MBD=∠A,∴BD∥AN.
10.(2018江西,15,6分)如图,在四边形ABCD中,AB∥CD,AB=2CD,E为AB的中点.请仅用 分别按下列要求画图(保留画图痕迹).(1)在图1中,画出△ABD的BD边上的中线;(2)在图2中,若BA=BD,画出△ABD的AD边上的高.
解析 画法如图.(1)AF即为所求. (2)BH即为所求.
解题关键 本题考查复杂作图,解题的关键是灵活运用平行四边形的性质和三角形的重心及等腰三角 形三线合一等知识解决问题.
11.如图,已知△ABC,点D在边AC上. (1)作∠ADE,使∠ADE=∠ACB,DE交AB于点E;(尺规作图,保留作图痕迹,不写作法)(2)若BC=5,点D是AC的中点,求DE的长.
解析 (1)如图,∠ADE即为所求. (2)∵∠ADE=∠ACB,∴DE∥BC,∵点D是AC的中点,∴DE为△ABC的中位线,∴DE= BC= .
12.在△ABC中,∠ACB=90°,CD为△ABC的角平分线.(1)求作:线段CD的垂直平分线EF,分别交AC、BC于点E、F,垂足为O(要求尺规作图,保留作图痕迹,不写 作法);(2)求证:△COE≌△COF;(3)连接DE、DF,判断四边形CEDF是什么特殊四边形,并说明理由.
解析 (1)如图. (2分)(2)证明:∵EF垂直平分CD,∴∠COE=∠COF=90°,∵CD平分∠ACB,∴∠ECO=∠FCO, (3分)
在△COE和△COF中, ∴△COE≌△COF(ASA). (5分)(3)四边形CEDF是正方形. (6分)理由如下:由(1)得CE=DE,CF=DF,由(2)得CE=CF,∴CE=ED=DF=CF,∴四边形CEDF是菱形,又∵∠ACB=90°,∴四边形CEDF是正方形. (8分)
13.(2020漳州一检,22)如图,在Rt△ABC中,∠ACB=90°,CD平分∠ACB交AB于点D.(1)在AC边上求作一点E,使得△ADE∽△ABC;(要求:尺规作图,不写作法,保留作图痕迹)(2)在(1)的条件下,若AC=15,BC=10,求DE的长.
解析 (1)作法一:如图1. 点E就是所求作的点. (4分)作法二:如图2. 点E就是所求作的点. (4分)
中考数学总复习 01第一章 数与式 PPT课件(福建专用): 这是一份中考数学总复习 01第一章 数与式 PPT课件(福建专用),文件包含§11实数ppt、§12代数式ppt、§13分式ppt等3份课件配套教学资源,其中PPT共180页, 欢迎下载使用。
中考数学总复习08第八章热点题型探究PPT课件(安徽专用): 这是一份中考数学总复习08第八章热点题型探究PPT课件(安徽专用),文件包含§83几何探究型ppt、§86开放探究型ppt、§85阅读理解型ppt、§84二次函数综合应用型ppt、§81选择填空压轴题的题型探究ppt、§82观察归纳型ppt等6份课件配套教学资源,其中PPT共255页, 欢迎下载使用。
中考数学总复习 06第六章 空间与图形 PPT课件(福建专用): 这是一份中考数学总复习 06第六章 空间与图形 PPT课件(福建专用),文件包含§61图形的轴对称平移与旋转ppt、§62图形的相似ppt、§63解直角三角形ppt、§64视图与投影ppt等4份课件配套教学资源,其中PPT共240页, 欢迎下载使用。












