中考数学总复习08第八章热点题型探究PPT课件（安徽专用）

这是一份中考数学总复习08第八章热点题型探究PPT课件（安徽专用），文件包含§83几何探究型ppt、§86开放探究型ppt、§85阅读理解型ppt、§84二次函数综合应用型ppt、§81选择填空压轴题的题型探究ppt、§82观察归纳型ppt等6份课件配套教学资源，其中PPT共255页， 欢迎下载使用。

1.(2020新疆,8,5分)二次函数y=ax2+bx+c的图象如图所示,则一次函数y=ax+b和反比例函数y= 在同一平面直角坐标系中的图象可能是 (　　 )  
答案    D　由抛物线开口向上可得a>0.∵抛物线的对称轴x=- 在y轴右侧,∴- >0,而a>0,∴b<0.由抛物线与y轴的交点在y轴正半轴上可得c>0.当a>0,b<0时,一次函数y=ax+b的图象经过第一、三、四象限;当c>0时,反比例函数y= 的图象经过第一、三象限,故选D.
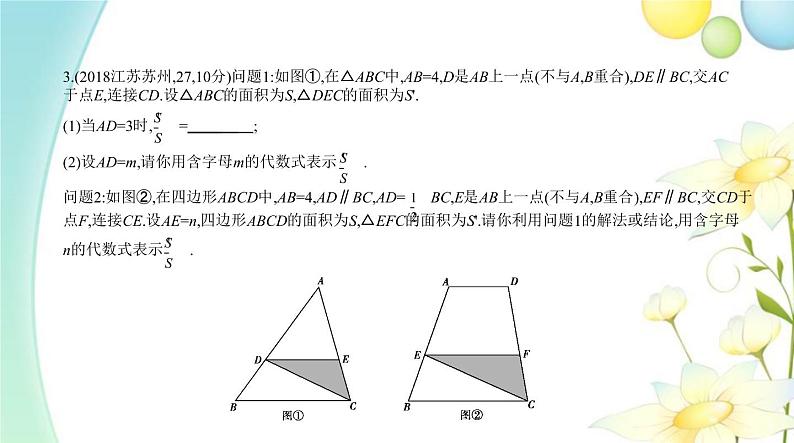
2.(2018安徽合肥瑶海一模,9)在同一直角坐标系中,函数y=mx+m和函数y=-mx2+2x+2(m是常数,且m≠0)的 图象可能是 (　 　) 
答案    D　当m>0时,函数y=mx+m单调递增,且在y轴上的截距为正,函数y=-mx2+2x+2的图象开口向下,其 对称轴在y轴右侧.当m<0时,函数y=mx+m单调递减,且在y轴上的截距为负,函数y=-mx2+2x+2的图象开口 向上,其对称轴在y轴左侧.满足上述条件的只有D选项.
3.(2018安徽合肥庐阳一模,10)反比例函数y1= 的图象与以y轴为对称轴的二次函数y2=ax2+bx+c的图象如图所示,则函数y=ax2+(b-k)x+c的图象可能是 (　 　)  
答案    A　∵反比例函数y1= 的图象在第二、四象限,∴k<0,由以y轴为对称轴的二次函数y2=ax2+bx+c的图象得a>0,b=0,c<0,∴b-k>0,∴函数y=ax2+(b-k)x+c的图象开口向上,且对称轴在y轴的左侧,并与y轴的 负半轴相交,故选A.
4.(2020安徽志诚教育十校联盟二模,10)如图,已知△ABC和△DEF均为等腰直角三角形,AB=2,DE=1,E、 B、F、C在同一条直线上,开始时点B与点F重合,让△DEF沿直线BC向右移动,最后点C与点E重合,设两 三角形重合部分的面积为y,点F移动的距离为x,则y关于x的大致图象是 (　 　) 
答案    A　当05.(2018安徽蚌埠六中联考,10)如图,正方形ABCD中,AB=4 cm,点E、F同时从C点出发,以1 cm/s的速度分 别沿C→B→A、C→D→A运动,到点A时停止运动.设运动时间为t(s),△AEF的面积为S(cm2),则S(cm2)与t (s)的函数关系可用图象表示为 (　 　) 
答案    D　当0≤t≤4时,S=S正方形ABCD-S△ADF-S△ABE-S△CEF=4×4- ×4×(4-t)- ×4·(4-t)- ·t·t=- t2+4t=- (t-4)2+8;当4题型二　线段的最值问题
1. (2020安徽合肥五十中二模,10)如图,等边△ABC的边长为4,点D是边AC上的一动点,连接BD,以BD为斜 边向上作等腰Rt△BDE,连接AE,则AE的最小值为 (　 　) A.1　    B. 　    C.2　    D.2 -1
答案    B　如图,过点B作BH⊥AC于H点,作射线HE, ∵△ABC是等边三角形,BH⊥AC,∴AH=2=CH,∵∠BED=∠BHD=90°,∴B、D、H、E四点共圆,∴∠BHE=∠BDE=45°,∴点E在∠AHB的角平分线上运动,∴当AE⊥EH时,AE最小,∵∠AHE=45°,∴AH= AE=2,∴AE的最小值为 .故选B.
思路分析　过点B作BH⊥AC于H点,作射线HE,可证B、D、H、E四点共圆,可得∠BHE=∠BDE=45°,则 点E在∠AHB的角平分线上运动,故当AE⊥EH时,AE最小,由此求解.
2.(2020新疆,15,5分)如图,在△ABC中,∠A=90°,∠B=60°,AB=2,若D是BC边上的动点,则2AD+DC的最小 值为　　 　    . 
解析　作△ABC关于BC对称的△EBC,则∠ACB=∠ECB=30°,过A作AF⊥CE于F,交BC于D,则 DC=DF. 此时AD+ DC最小,即为AF的长度.易求得AC=2 ,因此AF=3,∴2AD+DC的最小值为2×3=6.
解后反思　此题主要考查了利用特殊角的三角函数求线段长以及线段和的最值问题,难度较大.如何将  DC转化为DF的长是难点,充分利用含30°角的直角三角形的性质,将AD+ DC转化为AD+DF,然后利用“垂线段最短”的性质巧妙解决.
一题多解　如图所示,作点A关于BC的对称点A',连接AA'交BC于点H,连接A'D,过D作DE⊥AC于E.在Rt△ABH中,∠B=60°,AB=2,∴AH= ,∴AA'=2 ,在Rt△CDE中,DE= CD,即2DE=DC,∴2AD+DC=2(AD+DE).∵A与A'关于BC对称,∴AD=A'D,∴AD+DE=A'D+DE,∴当A',D,E在同一直线上时,AD+DE的最小值等于A'E的长,在Rt△AA'E中,A'E=sin 60°·AA'= ×2 =3,∴AD+DE的最小值为3,即2AD+DC的最小值为6,故答案为6.
3.(2019湖北黄冈,16,3分)如图,AC,BD在AB的同侧,AC=2,BD=8,AB=8.点M为AB的中点.若∠CMD=120°, 则CD的最大值为　　 　    . 
解析　如图,设点A关于CM的对称点为A',点B关于DM的对称点为B',当A',B'都在CD上时,CD有最大值.连 接MA',MB',则△MAC≌△MA'C,△MBD≌△MB'D,∴CA=CA'=2,BD=B'D=8,∠AMC=∠A'MC,∠BMD=∠B'MD,∵M为AB的中点,∴MA'=MA=MB=MB'=4,∵∠CMD=120°,∴∠AMC+∠BMD=60°,∴∠ A'MC +∠B'MD=60°,∴∠A'MB'=60°,∴A'B'=4,∴CD的最大值=CA'+A'B'+B'D=14. 
4.(2018江苏苏州,18,3分)如图,已知AB=8,P为线段AB上的一个动点,分别以AP,PB为边在AB的同侧作菱 形APCD和菱形PBFE,点P,C,E在一条直线上,∠DAP=60°.M,N分别是对角线AC,BE的中点.当点P在线段 AB上移动时,点M,N之间的距离最短为　 　    (结果保留根号). 
解析　连接PD、DF、PF,∵在菱形APCD和菱形PBFE中,M,N分别是对角线AC,BE的中点,∴PD经过点M,PF经过点N,且M,N分别是PD,PF的中点,∴MN是△PDF的中位线,∴MN= FD,∴当FD最短时,MN最短,∵AD∥BF,∠DAP=60°,AB=8,∴FD的最小值为AB·sin 60°=8× =4 ,∴MN的最小值为 FD=2 .
5.(2018贵州贵阳,15,4分)如图,在△ABC中,BC=6,BC边上的高为4,在△ABC的内部作一个矩形EFGH,使 EF在BC边上,另外两个顶点分别在AB,AC边上,则对角线EG长的最小值为　　 　    . 
解析　如图,作AM⊥BC于点M,交HG于点N,设HE=x.由题意知,AM=4,BC=6. ∵四边形EFGH是矩形,∴HG∥EF,∴△AHG∽△ABC,∴ = ,即 = ,∴HG= ,∴EG2=HG2+HE2= +x2
= =  + (0题型三　几何图形多解问题
1. (2020安徽二模,14)定义:对于平面直角坐标系xOy中的线段PQ和点M,在△MPQ中,当PQ边上的高为2  时,称点M为PQ的等高点”,称此时MP+MQ的值为PQ的“等高距离”.已知P(1,2),Q(3,4),当PQ的“等高距离”最小时,点M的坐标为　　　     .
答案　(4,1)或(0,5)
解析　如图,由题意可知点M在直线EF或直线E'F'上运动. 作点P关于直线EF的对称点P',连接QP'交直线EF于点M(4,1),此时PM+MQ的值最小;作点P关于直线E'F' 的对称点P″,连接QP″交直线E'F'于点M'(0,5),此时PM'+M'Q的值最小.综上,满足条件的点M的坐标为(4,1)或(0,5).
2.(2020安徽志诚教育十校联盟二模,14)若反比例函数y=- 的图象上有两个不同的点,它们关于y轴的对称点都在一次函数y=-x+m的图象上,则m的取值范围是　 　　    .
答案    m>2 或m<-2 
解析　∵反比例函数y=- 的图象上有两个不同的点,它们关于y轴的对称点在一次函数y=-x+m的图象上,∴y= 与一次函数y=-x+m的图象有两个不同的交点,即方程x2-mx+2=0有两个不同的实数根,∴Δ=m2-8>0,∴m>2 或m<-2 .
3.(2019安徽铜陵一模,14)小南利用几何画板画图,探索结论,他先画∠MAN=90°,在射线AM上取一点B,在 射线AN上取一点C,连接BC,再作点A关于直线BC的对称点D,连接AD、BD,得到如图所示的图形,移动点 C,小南发现:当AD=BC时,∠ABD=90°.请你继续探索,当2AD=BC时,∠ABD的度数是　 　　    . 
答案　30°或150°
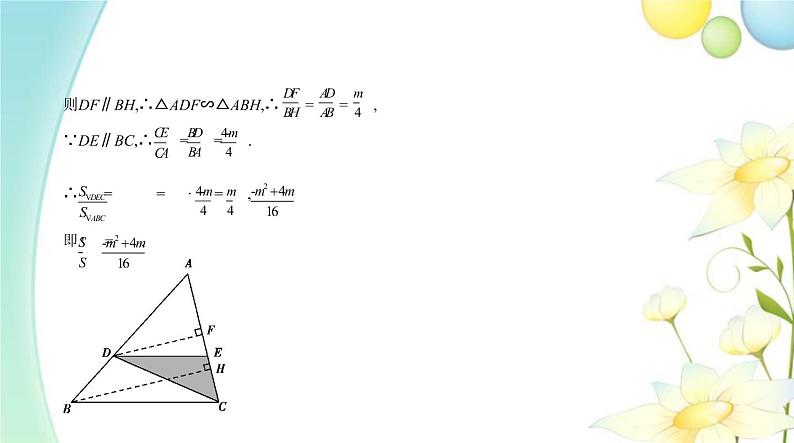
解析　分两种情况:当AB>AC时,如图, 取BC的中点E,连接AE,DE,则AE=DE= BC,即BC=2AE=2DE,又∵BC=2AD,∴AD=AE=DE,∴△ADE是等边三角形,∴∠AED=60°,又∵BC垂直平分AD,∴∠AEC=30°,又∵BE=AE,∴∠ABC= ∠AEC=15°,
∴∠ABD=2∠ABC=30°.当AB思路分析　分两种情况,取BC的中点E,连接AE,DE,依据直角三角形斜边上中线的性质,即可得到△ADE 是等边三角形,进而得出∠ABD的度数.
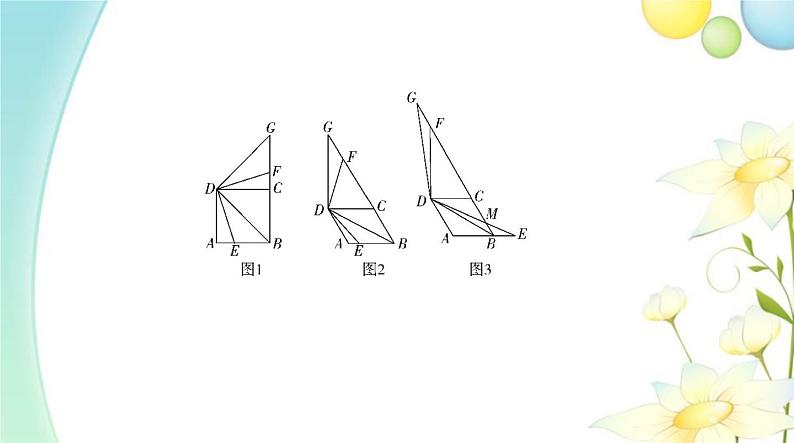
4.(2018安徽巢湖三中二模,14)如图,△ABC中,∠C=90°,AC=20,BC=15,点D在AC上(D与点A,C不重合),点E 在BC上(E与点B,C不重合),且DE∥AB.在AB上找一点P,使得△PDE为等腰直角三角形,则△PDE的斜边 长为　　 　    . 
答案      或 
解析　当∠EDP=90°时,如图1,设PD=DE=x,∵DE∥AB,∴△CDE∽△CAB,在Rt△ACB中,∵AC=20,BC=15,∴AB=25,则△ABC的AB边上的高为12,∴ = ,解得x= ,即DE= ,∴△PDE的斜边长为  ;当∠DEP=90°时,如图2,设EP=DE=x,同理可得,△PDE的斜边长为  ;当∠DPE=90°时,如图3,由等腰直角三角形的性质得P到DE的距离为 DE,设DE=x,∵DE∥AB,∴△CDE∽△CAB,∴ = ,解得x= ,即△PDE的斜边长为 .
综上,△PDE的斜边长为  或 .  
思路分析　分∠EDP=90°、∠DEP=90°、∠DPE=90°三种情况进行讨论,求解即可.
(2020浙江丽水,16)图1是一个闭合时的夹子,图2是该夹子的主视示意图,夹子两边为AC,BD(点A与点B重 合),点O是夹子转轴位置,OE⊥AC于点E,OF⊥BD于点F,OE=OF=1 cm,AC=BD=6 cm,CE=DF,CE∶AE= 2∶3.按图示方式用手指按夹子,夹子两边绕点O转动.(1)当E,F两点的距离最大时,以点A,B,C,D为顶点的四边形的周长是　　　     cm.(2)当夹子的开口最大(即点C与点D重合)时,A,B两点的距离为　　 　     cm. 
答案　(1)16　(2) 
解析　(1)当E,F两点的距离最大时,E,O,F三点共线,四边形ACDB是矩形,∵OE=OF=1 cm,∴EF=2 cm,∴AB=CD=2 cm,∴四边形ABCD的周长为2+2+6+6=16 cm.(2)如图,连接EF交OC于H.由题意CE=CF= ×6=  cm, 又∵OE=OF=1 cm,∴CO垂直平分线段EF,