

2021-2022学年广东省东莞市十校联考七年级(上)期末数学试卷 解析版
展开
这是一份2021-2022学年广东省东莞市十校联考七年级(上)期末数学试卷 解析版,共17页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
2021-2022学年广东省东莞市十校联考七年级(上)期末数学试卷
一、选择题(每小题3分共30分)
1.(3分)﹣7的绝对值是( )
A.7 B.﹣7 C. D.﹣
2.(3分)2021年党中央首次颁发“光荣在党50年”纪念章,约7100000名党员获此纪念章.数7100000用科学记数法表示为( )
A.71×105 B.7.1×105 C.7.1×106 D.0.71×107
3.(3分)单项式2a2b的系数和次数分别是( )
A.2,2 B.2,3 C.3,2 D.4,2
4.(3分)下列各数中,最小的数是( )
A.﹣2 B.0 C.﹣6 D.3
5.(3分)下列各对数中,相等的一对数是( )
A.(﹣2)3与﹣23 B.﹣22与(﹣2)2
C.﹣(﹣3)与﹣|﹣3| D.与
6.(3分)下面计算正确的是( )
A.2x2﹣x2=1 B.4a2+2a3=6a5
C.5+m=5m D.﹣0.25ab+ab=0
7.(3分)根据等式的性质,下列变形错误的是( )
A.若a=b,则a﹣1=b﹣1 B.若,则a=b
C.若a=b,则﹣3a=﹣3b D.若ac=bc,则a=b
8.(3分)如图是一个小正方体的展开图,把展开图折叠成小正方体后,有“害”字一面的相对面上的字是( )
A.了 B.我 C.的 D.国
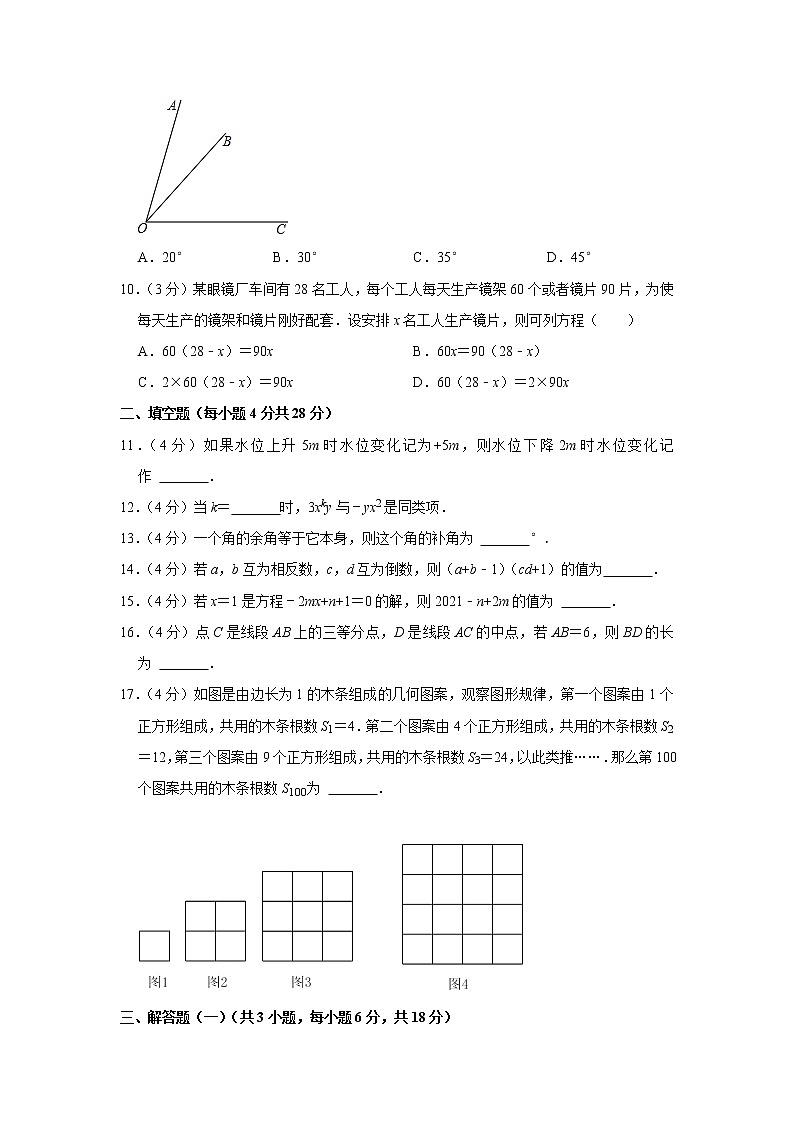
9.(3分)如图,已知∠AOB:∠BOC=2:3,∠AOC=75°,那么∠AOB=( )
A.20° B.30° C.35° D.45°
10.(3分)某眼镜厂车间有28名工人,每个工人每天生产镜架60个或者镜片90片,为使每天生产的镜架和镜片刚好配套.设安排x名工人生产镜片,则可列方程( )
A.60(28﹣x)=90x B.60x=90(28﹣x)
C.2×60(28﹣x)=90x D.60(28﹣x)=2×90x
二、填空题(每小题4分共28分)
11.(4分)如果水位上升5m时水位变化记为+5m,则水位下降2m时水位变化记作 .
12.(4分)当k= 时,3xky与﹣yx2是同类项.
13.(4分)一个角的余角等于它本身,则这个角的补角为 °.
14.(4分)若a,b互为相反数,c,d互为倒数,则(a+b﹣1)(cd+1)的值为 .
15.(4分)若x=1是方程﹣2mx+n+1=0的解,则2021﹣n+2m的值为 .
16.(4分)点C是线段AB上的三等分点,D是线段AC的中点,若AB=6,则BD的长为 .
17.(4分)如图是由边长为1的木条组成的几何图案,观察图形规律,第一个图案由1个正方形组成,共用的木条根数S1=4.第二个图案由4个正方形组成,共用的木条根数S2=12,第三个图案由9个正方形组成,共用的木条根数S3=24,以此类推…….那么第100个图案共用的木条根数S100为 .
三、解答题(一)(共3小题,每小题6分,共18分)
18.(6分)计算:﹣12×(﹣9)+16÷(﹣2)3﹣|﹣4×5|.
19.(6分)先化简,再求值:﹣3(x2y﹣xy2)﹣(﹣3x2y+2xy2)+xy,其中x=2,y=﹣.
20.(6分)解方程:.
四、解答题(二)(共3小题,每小题8分,共24分)
21.(8分)北大登山队以二号营地为基准,开始向距二号营地500米的顶峰冲击,他们记向上为正,行进过程记录如下:(单位:米):+150,﹣35,﹣40,+210,﹣32,+20,﹣18,﹣5,+20,+85,﹣25.
(1)他们最终有没有登上顶峰?若没有,距顶峰还有多少米?
(2)登山时,若5名队员在记录的行进路线上都使用了氧气,且每人每米要消耗氧气0.05升,则他们共耗氧多少升?
22.(8分)如图,铁片正面是直角三角形,中间有一个半径为r的圆孔,厚度为h.
(1)用式子表示这块铁片的体积V;
(2)若a=8cm,r=1cm,h=0.5cm,求V的值.(结果精确到0.1cm3)
23.(8分)如图,点C、D是线段AB上两点,AC:BC=3:2,点D为AB的中点.
(1)如图1所示,若AB=40,求线段CD的长.
(2)如图2所示,若E为AC的中点,ED=7,求线段AB的长.
五、解答题(三)(共2小题,每小题10分,共20分)
24.(10分)某小区建完之后,需要做内墙粉刷装饰,现有甲、乙两个工程队都想承包这项工程,已知甲工程队每天能粉刷160个房间,乙工程队每天能粉刷240个房间.且单独粉刷这些墙面甲工程队比乙工程队要多用20天,在粉刷的过程中,该开发商要付甲工程队每天费用1600元,付乙工程队每天费用2600元.
(1)求这个小区共有多少间房间?
(2)为了尽快完成这项工程,若先由甲、乙两个工程队按原粉刷速度合作一段时间后,甲工程队停工了,而乙工程队每天的粉刷速度提高25%,乙工程队单独完成剩余部分,且乙工程队的全部工作时间是甲工程队的工作时间的2倍还多4天,求乙工程队共粉刷多少天?
(3)经开发商研究制定如下方案:
方案一:由甲工程队单独完成;
方案二:由乙工程队单独完成;
方案三:按(2)问方式完成:
请你通过计算帮开发商选择一种既省时又省钱的粉刷方案.
25.(10分)一副三角板按如图1方式拼接在一起,其中边OA、OC与直线EF重合,∠AOB=45°,∠COD=60°.
(1)求图1中∠BOD的度数.
(2)如图2,三角板COD固定不动,将三角板AOB绕点O按顺时针方向旋转一个角度α(即∠AOE=α),在转动过程中两个三角板一直处于直线EF的上方.
①当OB平分OA、OC、OD其中的两边组成的角时,求满足要求的所有旋转角度α的值;
②在转动过程中是否存在∠BOC=2∠AOD?若存在,求此时α的值;若不存在,请说明理由.
2021-2022学年广东省东莞市十校联考七年级(上)期末数学试卷
参考答案与试题解析
一、选择题(每小题3分共30分)
1.(3分)﹣7的绝对值是( )
A.7 B.﹣7 C. D.﹣
【分析】根据绝对值的性质解答,当a是负有理数时,a的绝对值是它的相反数﹣a.
【解答】解:|﹣7|=7.
故选:A.
2.(3分)2021年党中央首次颁发“光荣在党50年”纪念章,约7100000名党员获此纪念章.数7100000用科学记数法表示为( )
A.71×105 B.7.1×105 C.7.1×106 D.0.71×107
【分析】根据科学记数法的定义即可判断,将一个较大或较小的数字写成a×10n的形式,其中1≤a<10且n为整数.
【解答】解:根据科学记数法的定义,将一个较大或较小的数字写成a×10n的形式,其中1≤a<10且n为整数.
∴7100000=7.1×106.
故选:C.
3.(3分)单项式2a2b的系数和次数分别是( )
A.2,2 B.2,3 C.3,2 D.4,2
【分析】根据单项式的次数是字母指数和,单项式的系数是数字因数,可得答案.
【解答】解:2a2b的系数和次数分别是2,3.
故选:B.
4.(3分)下列各数中,最小的数是( )
A.﹣2 B.0 C.﹣6 D.3
【分析】根据负数都小于0,负数都小于正数,得出﹣2和﹣6小,根据两个负数比较大小,其绝对值大的反而小,即可得出答案.
【解答】解:∵﹣6<﹣2<0<3,
∴最小的数是﹣6,
故选:C.
5.(3分)下列各对数中,相等的一对数是( )
A.(﹣2)3与﹣23 B.﹣22与(﹣2)2
C.﹣(﹣3)与﹣|﹣3| D.与
【分析】利用有理数的乘方运算法则及绝对值和相反数的概念进行计算或化简,从而作出判断.
【解答】解:A、(﹣2)3=﹣8,﹣23=﹣8,(﹣2)3与﹣23相等,故此选项符合题意;
B、﹣22=﹣4,(﹣2)2=4,﹣22与(﹣2)2不相等,故此选项不符合题意;
C、﹣(﹣3)=3,﹣|﹣3|=﹣3,﹣(﹣3)与﹣|﹣3|不相等,故此选项不符合题意;
D、,()2=,与()2不相等,故此选项不符合题意;
故选:A.
6.(3分)下面计算正确的是( )
A.2x2﹣x2=1 B.4a2+2a3=6a5
C.5+m=5m D.﹣0.25ab+ab=0
【分析】合并同类项的法则:把同类项的系数相加,所得结果作为系数,字母和字母的指数不变.据此逐一判断即可.
【解答】解:A.2x2﹣x2=x2,故本选项不合题意;
B.4a2与2a3不是同类项,所以不能合并,故本选项不合题意;
C.5与m不是同类项,所以不能合并,故本选项不合题意;
D.﹣0.25ab+ab=0,故本选项符合题意.
故选:D.
7.(3分)根据等式的性质,下列变形错误的是( )
A.若a=b,则a﹣1=b﹣1 B.若,则a=b
C.若a=b,则﹣3a=﹣3b D.若ac=bc,则a=b
【分析】根据等式的基本性质解决此题.
【解答】解:A.根据等式的基本性质,若a=b,则a﹣1=b﹣1,故A正确,那么A不符合题意.
B.根据等式的基本性质,若,得,则a=b,故B正确,那么B不符合题意.
C.根据等式的基本性质,若a=b,则﹣3a=﹣3b,故C正确,那么C不符合题意.
D.根据等式的基本性质,由ac=bc,当c≠0,得a=b,故D错误,那么D符合题意.
故选:D.
8.(3分)如图是一个小正方体的展开图,把展开图折叠成小正方体后,有“害”字一面的相对面上的字是( )
A.了 B.我 C.的 D.国
【分析】根据正方体表面展开图的特征进行判断即可.
【解答】解:根据正方体表面展开图的“相间、Z端是对面”可得,
“厉”与“了”相对,
“我”与“国”相对,
“害”与“的”相对,
故选:C.
9.(3分)如图,已知∠AOB:∠BOC=2:3,∠AOC=75°,那么∠AOB=( )
A.20° B.30° C.35° D.45°
【分析】由∠AOB:∠BOC=2:3,可得∠AOB=∠AOC进而求出答案,做出选择.
【解答】解:∵∠AOB:∠BOC=2:3,∠AOC=75°,
∴∠AOB=∠AOC=×75°=30°,
故选:B.
10.(3分)某眼镜厂车间有28名工人,每个工人每天生产镜架60个或者镜片90片,为使每天生产的镜架和镜片刚好配套.设安排x名工人生产镜片,则可列方程( )
A.60(28﹣x)=90x B.60x=90(28﹣x)
C.2×60(28﹣x)=90x D.60(28﹣x)=2×90x
【分析】设安排x名工人生产镜片,则(28﹣x)人生产镜架,根据2个镜片和1个镜架恰好配一套,列方程即可.
【解答】解:设安排x名工人生产镜片,
由题意得,90x=2×60(28﹣x).
故选:C.
二、填空题(每小题4分共28分)
11.(4分)如果水位上升5m时水位变化记为+5m,则水位下降2m时水位变化记作 ﹣2m .
【分析】根据正负数的意义,直接写出答案即可.
【解答】解:水位上升5m时水位变化记为+5m,则水位下降2m时水位变化记作﹣2m,
故答案为:﹣2m.
12.(4分)当k= 2 时,3xky与﹣yx2是同类项.
【分析】根据同类项的定义求解即可,所含字母相同,并且相同字母的指数也相同,这样的项叫做同类项.
【解答】解:∵3xky与﹣yx2是同类项,
∴k=2.
故答案为:2.
13.(4分)一个角的余角等于它本身,则这个角的补角为 135 °.
【分析】设这个角为x°,则2x=90,据此求出x,再根据补角的定义解答即可.
【解答】解:设这个角为x°,则
2x=90,
解得x=45,
∴这个角为45°,
∴这个角的补角为:180°﹣45°=135°.
故答案为:135.
14.(4分)若a,b互为相反数,c,d互为倒数,则(a+b﹣1)(cd+1)的值为 ﹣2 .
【分析】先根据相反数的性质和倒数的定义得出a+b=0,cd=1,再代入计算可得.
【解答】解:根据题意知a+b=0,cd=1,
则原式=(0﹣1)×(1+1)
=﹣1×2
=﹣2,
故答案为:﹣2.
15.(4分)若x=1是方程﹣2mx+n+1=0的解,则2021﹣n+2m的值为 2022 .
【分析】把x=1代入方程﹣2mx+n+1=0得长﹣2m+n+1=0,求出2m﹣n=1,再代入2021﹣n+2m求出答案即可.
【解答】解:把x=1代入方程﹣2mx+n+1=0得:﹣2m+n+1=0,
解得:2m﹣n=1,
所以2021﹣n+2m
=2021+(2m﹣n)
=2021+1
=2022,
故答案为:2022.
16.(4分)点C是线段AB上的三等分点,D是线段AC的中点,若AB=6,则BD的长为 5或4 .
【分析】根据点C是线段AB上的三等分点,分两种情况画图进行计算即可.
【解答】解:如图,
∵点C是线段AB上的三等分点,
∴AB=3AC,即AC=2,
∵D是线段AC的中点,
∴AD=AC=1,
∴BD=AB﹣AD=6﹣1=5;
如图,
∵点C是线段AB上的三等分点,
∴AB=3BC,即BC=2,AC=4,
∵D是线段AC的中点,
∴AD=AC=2,
∴BD=AB﹣AD=6﹣2=4;
则BD的长为5或4.
故答案为:5或4.
17.(4分)如图是由边长为1的木条组成的几何图案,观察图形规律,第一个图案由1个正方形组成,共用的木条根数S1=4.第二个图案由4个正方形组成,共用的木条根数S2=12,第三个图案由9个正方形组成,共用的木条根数S3=24,以此类推…….那么第100个图案共用的木条根数S100为 20200 .
【分析】通过第1、2、3和4个图案找出普遍规律,进而得出第n个图案的规律为Sn=4n+2n×(n﹣1),得出结论即可.
【解答】解:观察图形可知:
第1个图案由1个小正方形组成,共用的木条根数S1=4×1,即S1=4×1+2×1×(1﹣1);
第2个图案由4个小正方形组成,共用的木条根数S2=4×2+2×2;即S2=4×2+2×2×(2﹣1);
第3个图案由9个小正方形组成,共用的木条根数S3=4×3+2×3;即S3=4×3+2×3×(3﹣1);
第4个图案由16个小正方形组成,共用的木条根数S4=4×4+2×4;即S4=4×4+2×4×(4﹣1);
…,
由此发现规律是:
第n个图案由n2个小正方形组成,共用的木条根数Sn=4n+2n×(n﹣1),
当n=100时,S100=4×100+200×(100﹣1)=20200,
故答案为:20200.
三、解答题(一)(共3小题,每小题6分,共18分)
18.(6分)计算:﹣12×(﹣9)+16÷(﹣2)3﹣|﹣4×5|.
【分析】先算乘方和去绝对值,然后再算乘除法,最后算加减法即可.
【解答】解:﹣12×(﹣9)+16÷(﹣2)3﹣|﹣4×5|
=﹣1×(﹣9)+16÷(﹣8)﹣20
=9+(﹣2)+(﹣20)
=﹣13.
19.(6分)先化简,再求值:﹣3(x2y﹣xy2)﹣(﹣3x2y+2xy2)+xy,其中x=2,y=﹣.
【分析】原式去括号合并得到最简结果,把x与y的值代入计算即可求出值.
【解答】解:原式=﹣3x2y+xy2+3x2y﹣2xy2+xy,
=﹣xy2+xy,
当x=2,y=﹣时,
原式=﹣2×+2×=﹣﹣1=﹣.
20.(6分)解方程:.
【分析】方程去分母,去括号,移项,合并同类项,系数化为1即可.
【解答】解:,
去分母,得2(3x﹣1)﹣(4x﹣1)=6,
去括号,得6x﹣2﹣4x+1=6,
移项,得6x﹣4x=6+2﹣1,
合并同类项,得2x=7,
系数化为1,x=.
四、解答题(二)(共3小题,每小题8分,共24分)
21.(8分)北大登山队以二号营地为基准,开始向距二号营地500米的顶峰冲击,他们记向上为正,行进过程记录如下:(单位:米):+150,﹣35,﹣40,+210,﹣32,+20,﹣18,﹣5,+20,+85,﹣25.
(1)他们最终有没有登上顶峰?若没有,距顶峰还有多少米?
(2)登山时,若5名队员在记录的行进路线上都使用了氧气,且每人每米要消耗氧气0.05升,则他们共耗氧多少升?
【分析】(1)根据有理数的加法,可得到达的地点,再根据有理数的减法,可得他们距顶峰的距离;
(2)根据路程乘以5个人的单位耗氧量,可得答案.
【解答】解:(1)+150﹣35﹣40+210﹣32+20﹣18﹣5+20+85﹣25=330(米),
500﹣330=170(米).
答:他们最终没有登顶,距顶峰还有170米;
(2)(+150+|﹣35|+|﹣40|+210+|﹣32|+20+|﹣18|+|﹣5|+20+85+|﹣25|)×(5×0.05)
=640×0.25
=160(升).
答:他们共耗氧气160升.
22.(8分)如图,铁片正面是直角三角形,中间有一个半径为r的圆孔,厚度为h.
(1)用式子表示这块铁片的体积V;
(2)若a=8cm,r=1cm,h=0.5cm,求V的值.(结果精确到0.1cm3)
【分析】(1)解题的关键是看成一个三棱柱的体积减去一个圆柱的体积,即可求得该铁片的体积.
(2)解题的关键是能正确表示相应图形的体积公式,代入题目中 已知的具体数值即可求得体积的具体数值.
【解答】解:(1)V铁片=V棱柱﹣V圆柱,
∴,
∴.
(2)
=×82×0.5﹣3.14×12×0.5
=16﹣1.57
=14.43
≈14.4(cm3).
∴V=14.4(cm3).
23.(8分)如图,点C、D是线段AB上两点,AC:BC=3:2,点D为AB的中点.
(1)如图1所示,若AB=40,求线段CD的长.
(2)如图2所示,若E为AC的中点,ED=7,求线段AB的长.
【分析】(1)根据题意易得到AD=BD=AB=20,BC=AB=16,再根据线段之间的和差关系求解即可;
(2)根据题意可推出AC=AB,AD=AB,AE=AC=×AB,再根据线段之间的和差关系求解即可.
【解答】解:(1)∵AB=40,点D是AB的中点,
∴AD=BD=AB=20,
又AC:BC=3:2,
∴BC=AB=16,
∴CD=BD﹣BC=20﹣16=4;
(2)∵AC:BC=3:2,点D为AB的中点,
∴AC=AB,AD=AB,
∵E为AC的中点,
∴AE=AC=×AB,
∴ED=AD﹣AE=AB﹣×AB=7,
解得AB=35.
五、解答题(三)(共2小题,每小题10分,共20分)
24.(10分)某小区建完之后,需要做内墙粉刷装饰,现有甲、乙两个工程队都想承包这项工程,已知甲工程队每天能粉刷160个房间,乙工程队每天能粉刷240个房间.且单独粉刷这些墙面甲工程队比乙工程队要多用20天,在粉刷的过程中,该开发商要付甲工程队每天费用1600元,付乙工程队每天费用2600元.
(1)求这个小区共有多少间房间?
(2)为了尽快完成这项工程,若先由甲、乙两个工程队按原粉刷速度合作一段时间后,甲工程队停工了,而乙工程队每天的粉刷速度提高25%,乙工程队单独完成剩余部分,且乙工程队的全部工作时间是甲工程队的工作时间的2倍还多4天,求乙工程队共粉刷多少天?
(3)经开发商研究制定如下方案:
方案一:由甲工程队单独完成;
方案二:由乙工程队单独完成;
方案三:按(2)问方式完成:
请你通过计算帮开发商选择一种既省时又省钱的粉刷方案.
【分析】(1)设乙工程队要刷x天,根据题意房间数量列出方程,再解即可;
(2)设甲工程队的工作时间为y天,则乙工程队的工作时间(2y+4)天,根据两队共粉刷9600间房间列出方程,再解即可;
(3)分别计算出三种方案的花费和时间,然后进行比较即可.
【解答】解:(1)设乙工程队要刷x天,由题意得:
240x=160(x+20),
解得:x=40,
240×40=9600(间),
答:这个小区共有9600间房间;
(2)设甲工程队的工作时间为y天,则乙工程队的工作时间(2y+4)天,由题意得:
160y+240y+240(1+25%)×(2y+4﹣y)=9600,
解得:y=12,
2y+4=2×12+4=28(天),
答:乙工程队共粉刷28天;
(3)方案一:由甲工程队单独完成,
时间:40+20=60(天),
60×1600=96000(元);
方案二:由乙工程队单独完成需要40天,
费用:40×2600=104000(元);
方案三:按(2)问方式完成,
时间:28天,
费用:12×(1600+2600)+(28﹣12)×2600=92000(元),
∵28<40<60,且92000<96000<104000,
∴方案三最合适,
答:选择方案三既省时又省钱的粉刷方案.
25.(10分)一副三角板按如图1方式拼接在一起,其中边OA、OC与直线EF重合,∠AOB=45°,∠COD=60°.
(1)求图1中∠BOD的度数.
(2)如图2,三角板COD固定不动,将三角板AOB绕点O按顺时针方向旋转一个角度α(即∠AOE=α),在转动过程中两个三角板一直处于直线EF的上方.
①当OB平分OA、OC、OD其中的两边组成的角时,求满足要求的所有旋转角度α的值;
②在转动过程中是否存在∠BOC=2∠AOD?若存在,求此时α的值;若不存在,请说明理由.
【分析】(1)根据平角的定义即可得到结论;
(2)①根据已知条件和角平分线的定义即可得到结论;
②当OA在OD的左侧时,当OA在OD的右侧时,列方程即可得到结论.
【解答】解:(1)∵∠AOB=45°,∠COD=60°,
∴∠BOD=180°﹣∠AOB﹣∠COD=75°;
(2)①当OB平分∠AOD时,
∵∠AOE=α,∠COD=60°,
∴∠AOD=180°﹣∠AOE﹣∠COD=120°﹣α,
∴∠AOB=∠AOD=60°﹣α=45°,
∴α=30°;
当OB平分∠AOC时,
∵∠AOC=180°﹣α,
∴∠AOB=90°﹣α=45°,
∴α=90°;
当OB平分∠DOC时,
∵∠DOC=60°,
∴∠BOC=30°,
∴α=180°﹣45°﹣30°=105°,
综上所述,旋转角度α的值为30°,90°,105°;
②当OA在OD的左侧时,则∠AOD=120°﹣α,∠BOC=135°﹣α,
∵∠BOC=2∠AOD,
∴135°﹣α=2(120°﹣α),
∴α=105°;
当OA在OD的右侧时,则∠AOD=α﹣120°,∠BOC=135°﹣α,
∵∠BOC=2∠AOD,
∴135°﹣α=2(α﹣120),
∴α=125°,
综上所述,当α=105°或125°时,存在∠BOC=2∠AOD.
相关试卷
这是一份2023-2024学年广东省东莞市五校联考七年级(上)期末数学试卷(含详细答案解析),共14页。试卷主要包含了选择题,填空题,计算题,解答题等内容,欢迎下载使用。
这是一份2023-2024学年广东省东莞市五校联考七年级(上)期末数学试卷(含解析),共14页。试卷主要包含了选择题,填空题,计算题,解答题等内容,欢迎下载使用。
这是一份2022-2023学年广东省东莞市八校联考九年级(上)期末数学试卷(含解析),共20页。试卷主要包含了选择题,填空题,计算题,解答题等内容,欢迎下载使用。









