数学第十七章 勾股定理综合与测试同步达标检测题

这是一份数学第十七章 勾股定理综合与测试同步达标检测题，共13页。试卷主要包含了单选题，填空题，解答题等内容，欢迎下载使用。
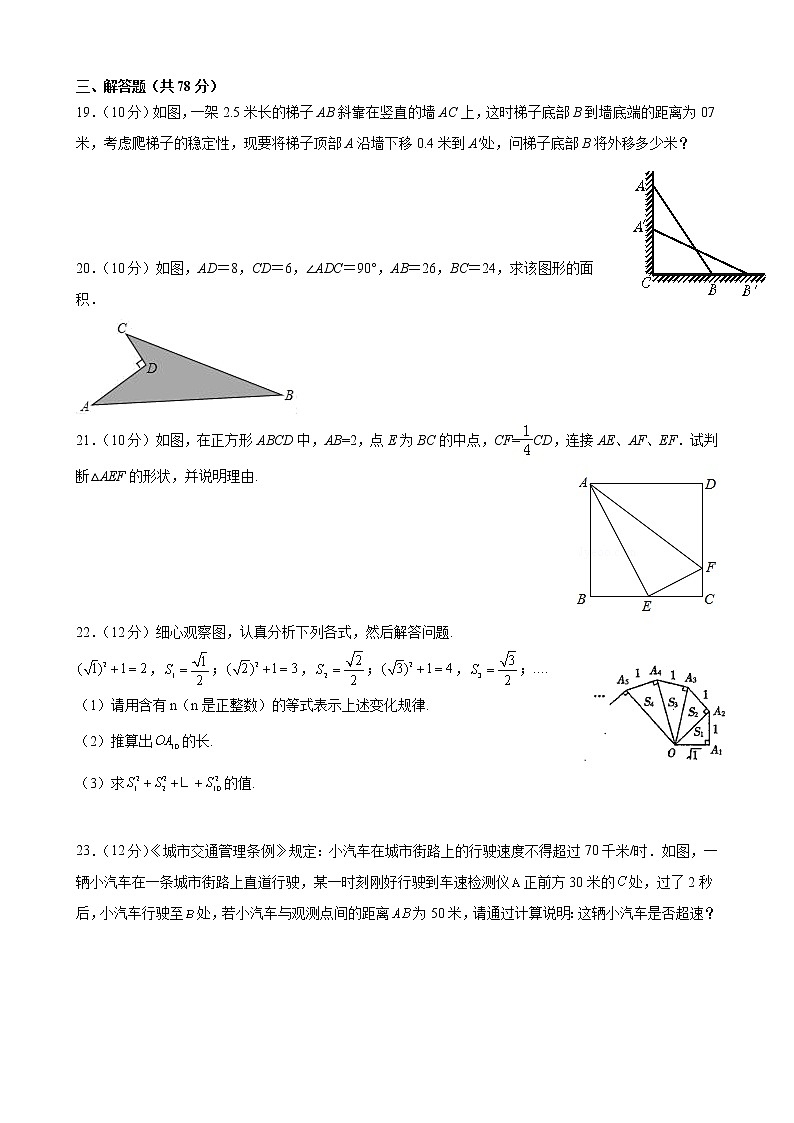
第十七章《勾股定理》测试卷全卷满分：150分；考试时间：100分钟；一、单选题（每小题4分，共40分）1．下列四组线段中，能组成直角三角形的是（    ）A．1，2，3 B．2，3，4 C．3，4，5 D．4，5，62．如图是一个直角三角形，它的未知边的长x等于　　 A．13 B． C．5 D．3．如图，字母B所代表的正方形的面积是　　A．12 B．144 C．13 D．1944．下列说法正确的是（    ）A．若a、b、c是△ABC的三边，则a2b2c2；B．若a、b、c是Rt△ABC的三边，则a2b2c2；C．若a、b、c是Rt△ABC的三边，∠A=90°，则a2b2c2；D．若a、b、c是Rt△ABC的三边，∠C=90°，则a2b2c2；5．满足下列条件的中，不是直角三角形的是　　A． B．C． D．6．如图，有一个水池，其底面是边长为16尺的正方形，一根芦苇AB生长在它的正中央，高出水面部分BC的长为2尺，如果把该芦苇沿与水池边垂直的方向拉向岸边，那么芦苇的顶部B恰好碰到岸边的B′，则这根芦苇AB的长是（　　）A．15尺 B．16尺 C．17尺 D．18尺7．如图图中，不能用来证明勾股定理的是（　　）A． B． C． D．8．已知一个直角三角形的两边长分别3和4，则第三边长是(   )A．5 B． C．25 D．5或9．如图，已知圆柱底面的周长为，圆柱的高为，在圆柱的侧面上，过点和点嵌有一圈金属丝，则这圈金属丝的周长最小为（    ）A． B． C． D．10．如图，将矩形纸片沿直线折叠，使点落在边的中点处，点落在点处，其中，则的长为（    ）A．3 B．4 C．4．5 D．5二、填空题（每小题4分，共32分）11．在△ABC中，AB＝c，AC＝b，BC＝a，当a、b、c满足_______时，∠B=90°．12．如图，一棵大树在一次强台风中于离地面处折断倒下，树干顶部在距离根部处，这棵大树在折断前的高度为__________．13．如图，学校有一块长方形草坪，有极少数人为了避开拐角走“捷径”，在草坪内走出了一条“路”，他们仅仅少走了________步路（假设步为米），却踩伤了花草．14．如图，要为一段高5m，长13m的楼梯铺上红地毯，至少需要红地毯______m．15．如图所示，在数轴上点所表示的数为，则的值为____________________．16．在△中，若三边长分别为9、12、15，则以两个这样的三角形拼成的长方形的面积为______.17．在直线l上依次摆放着七个正方形(如图所示)．已知斜放置的三个正方形的面积分别是a，b，c，正放置的四个正方形的面积依次是S1，S2，S3，S4，则S1＋S2＋S3＋S4＝_____．18．毕达哥拉斯学派提出了一个构造勾股数组的公式,根据该公式可以构造出如下勾股数组:(3,4,5),(5,12,13),(7,24,25),….分析上面勾股数组可以发现,4=1×(3+1),12=2×(5+1),24=3×(7+1),…,分析上面规律,第5个勾股数组为　    　.   三、解答题（共78分）19．（10分）如图，一架2.5米长的梯子AB斜靠在竖直的墙AC上，这时梯子底部B到墙底端的距离为0.7米，考虑爬梯子的稳定性，现要将梯子顶部A沿墙下移0.4米到A′处，问梯子底部B将外移多少米？  20．（10分）如图，AD＝8，CD＝6，∠ADC＝90°，AB＝26，BC＝24，求该图形的面积．21．（10分）如图，在正方形ABCD中，AB=2，点E为BC的中点，CF=CD，连接AE、AF、EF．试判断△AEF的形状，并说明理由.    22．（12分）细心观察图，认真分析下列各式，然后解答问题.，；，；，；....（1）请用含有n（n是正整数）的等式表示上述变化规律.（2）推算出的长.（3）求的值. 23．（12分）《城市交通管理条例》规定：小汽车在城市街路上的行驶速度不得超过70千米/时．如图，一辆小汽车在一条城市街路上直道行驶，某一时刻刚好行驶到车速检测仪正前方30米的处，过了2秒后，小汽车行驶至处，若小汽车与观测点间的距离为50米，请通过计算说明：这辆小汽车是否超速？24．（12分）如图(1),在△ABC中,BC=a,AC=b,AB=c，若∠C=90°，则有a2+b2=c2；如图(2)，△ABC为锐角三角形时，小明猜想a2+b2>c2，理由如下：设CD=x，在Rt△ADC中，AD2=b2-x2，在Rt△ADB中,AD2=c2-(a-x)2，则b2-x2=c2-(a-x)2，所以a2+b2=c2+2ax，因为a>0，x>0，所以2ax>0，所以a2+b2>c2，所以当△ABC为锐角三角形时a2+b2>c2.所以小明的猜想是正确的.(1)请你猜想,当△ABC为钝角三角形时，a2+b2与c2的大小关系；(2)证明你猜想的结论是否正确.        25．（12分）一块长方体木块的各棱长如图所示，一只蜘蛛在木块的一个顶点A处，一只苍蝇在这个长方体上和蜘蛛相对的顶点B处，蜘蛛急于捉住苍蝇，沿着长方体的表面向上爬．(1)如果D是棱的中点，蜘蛛沿“AD→DB”路线爬行，它从A点爬到B点所走的路程为多少？(2)若蜘蛛还走前面和右面这两个面，你认为“AD-DB"是最短路线吗？如果不是，请求出最短路程，如果是，请说明理由
参考答案一、选择题1．C解：A、12+22≠32，不能构成直角三角形，故不符合题意；
B、22+32≠42，不能构成直角三角形，故不符合题意；
C、32+42=52，能构成直角三角形，故符合题意；
D、42+52≠62，不能构成直角三角形，故不符合题意．
故选：C．2．B解：由勾股定理得：22+32=x2.所以，x= 故选B3．B解：如图，根据勾股定理我们可以得出：a2+b2＝c2a2＝25，c2＝169，b2＝169﹣25＝144，因此B的面积是144．故选B．4．D解：A、勾股定理只限于在直角三角形里应用，故错误； B、虽然给出的是直角三角形，但没有给出哪一个是直角，故B错误； C、在Rt△ABC中，直角所对的边是斜边，C中的斜边应为a，得出的表达式应为b2+c2=a2，故C也错误； D、符合勾股定理，正确．故答案为：D．5．D解：A、∵，∴，∴∠C=90°，所以△ABC是直角三角形，本选项不符合题意；B、由可设，∵，∴∠C=90°，所以△ABC是直角三角形，本选项不符合题意；C、∵，∴，∵∠A+∠B+∠C=180°，∴2∠A=180°，∴∠A=90°，所以△ABC是直角三角形，本选项不符合题意；D、由可设，∵∠A+∠B+∠C=180°，∴=180°，解得：，∴，所以△ABC不是直角三角形，本选项符合题意．故选：D．6．C解：依题意画出图形，设芦苇长AB=AB′=x尺，则水深AC=（x-2）尺，
因为B'E=16尺，所以B'C=8尺
在Rt△AB'C中，82+（x-2）2=x2，
解之得：x=17，
即芦苇长17尺．
故选C．7．D解：A，B，C都可以利用图形面积得出a，b，c的关系，即可证明勾股定理；故A，B，C选项不符合题意；D、不能利用图形面积证明勾股定理，故此选项正确．故选D．8．D解：∵，∴第三边长是5或．　故选D．9．A解：如图，把圆柱的侧面展开，得到矩形，则这圈金属丝的周长最小为的长度，圆柱底面的周长为，圆柱高为，，，，，这圈金属丝的周长最小为．故选：．10．D解：设，则．∵，四边形为矩形，点为的中点．∴，在中，由勾股定理得，即，解得．故选D．二、填空题11．a2+c2= b2解：∵a2+c2=b2时，△ABC是以AC为斜边的直角三角形，
∴当a、b、c满足a2+c2=b2时，∠B=90°．
故答案为：a2+c2=b2．12．8解：由勾股定理知，折断部分为5m,3+5=8m,所以大树高为8m.13．解：如图，∵在中，，∴ ，则少走的距离为：，∵步为米，∴少走了步．故答案为：．14．17解：根据勾股定理，楼梯水平长度为=12米，
则红地毯至少要12+5=17米长，故答案为：17．15．解：∵圆的半径为，∴A点表示的数为故答案为．16．108解：∵在△ABC中，三条边的长度分别为9、12、15，∵92+122=152，∴△ABC是直角三角形，∴用两个这样的三角形所拼成的长方形的面积是2××9×12=10817．a+c解：

∵∠ACB+∠DCE=90°，∠BAC+∠ACB=90°，
∴∠DCE=∠BAC，
∵AC=CE，∠ABC=∠CDE
∴△ABC≌△CDE，
∴BC=DE，
在直角△ABC中，AB2+BC2=AC2，
即，AB2+DE2=AC2，
∵S3=AB2，S4=DE2
∴S3+S4=c
同理S1+S2=a
故可得S1+S2+S3+S4=a+c，
故答案是： a+c．18．(11,60,61)解：由勾股数组：（3，4，5），（5，12，13），（7，24，25）…中，4=1×（3+1），12=2×（5+1），24=3×（7+1），…可得第4组勾股数中间的数为4×（9+1）=40，即勾股数为（9，40，41）；第5组勾股数中间的数为：5×（11+1）=60，即（11，60，61），故答案为（11，60，61）．三、解答题19．0.8米．解：在Rt△ABC中，∵AB=2.5米，BC=0.7米，
∴米，
又∵AA′=0.4米，
∴A′C=2.4-0.4=2米，
在Rt△A′B′C中，米，
则BB′=CB′-CB=1.5-0.7=0.8米．
故：梯子底部B外移0.8米．20．96解：连接AC，在Rt△ACD中，AD＝8，CD＝6，∴AC＝ ＝10，在△ABC中，∵AC2+BC2＝102+242＝262＝AB2，∴△ABC为直角三角形；∴图形面积为： 21．△AEF是直角三角形，理由见解析.解：△AEF是直角三角形，理由如下：在正方形ABCD中，∵AB=2，点E为BC的中点，CF=CD，∴AD=AB=2，BE=CE=1，CF =，DF=，∴由勾股定理得AE=AF=，EF=；∵AE2+EF2=，AF2= ，∴AE2+EF2=AF2，∴△AEF为直角三角形.22．（1），.（n是正整数）；（2）；（3）解：（1），.（n是正整数）（2）由（1）得，，即OAn2=n，∴.（3）.23．这辆小汽车超速解：根据题意，得AC=30m，AB=50m，∠C=90°，在Rt△ACB中， ，∴小汽车的速度；∴这辆小汽车超速．24．(1)a2+b2<c2；(2)证明见解析.解：（1）当△ABC为钝角三角形时，a2+b2与c2的大小关系为：a2+b2＜c2；（2）如图3，过点A作AD⊥BC于点D，设CD=x．在Rt△ADC中，AD2=b2﹣x2．在Rt△ADB中，AD2=c2﹣（a+x）2，∴b2﹣x2=c2﹣（a+x）2，∴a2+b2=c2﹣2ax．∵a＞0，x＞0，∴2ax＞0，∴a2+b2＜c2，∴当△ABC为钝角三角形时，a2+b2＜c2．25．（1）5+；（2）不是，6cm解：(1)从点A爬到点B所走的路程为AD+BD=+=5+．(2)不是，分三种情况讨论：①将下面和右面展到一个平面内，AB===2(cm)；②将前面与右面展到一个平面内，AB===6(cm)；③将前面与上面展到一个平面内，AB==4(cm)，∴蜘蛛从A点爬到B点所走的最短路程为6cm.