初中数学冀教版八年级下册第二十章 函数综合与测试一课一练

这是一份初中数学冀教版八年级下册第二十章 函数综合与测试一课一练，共24页。
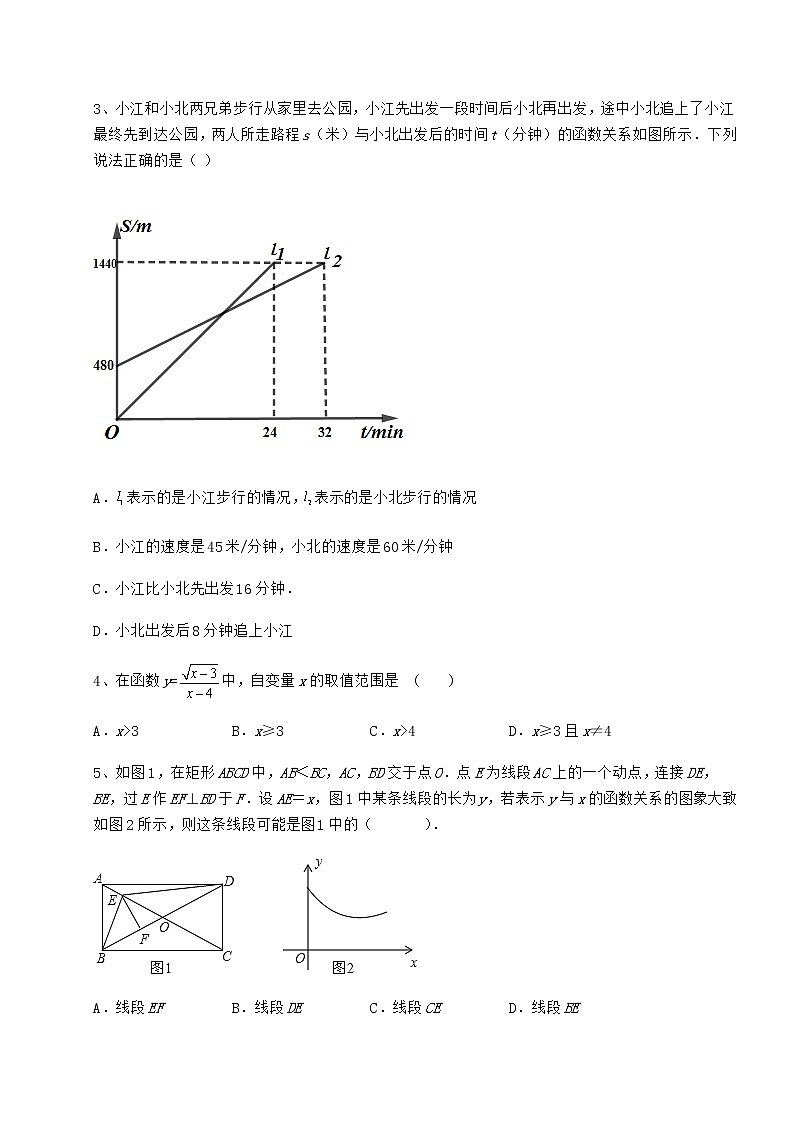
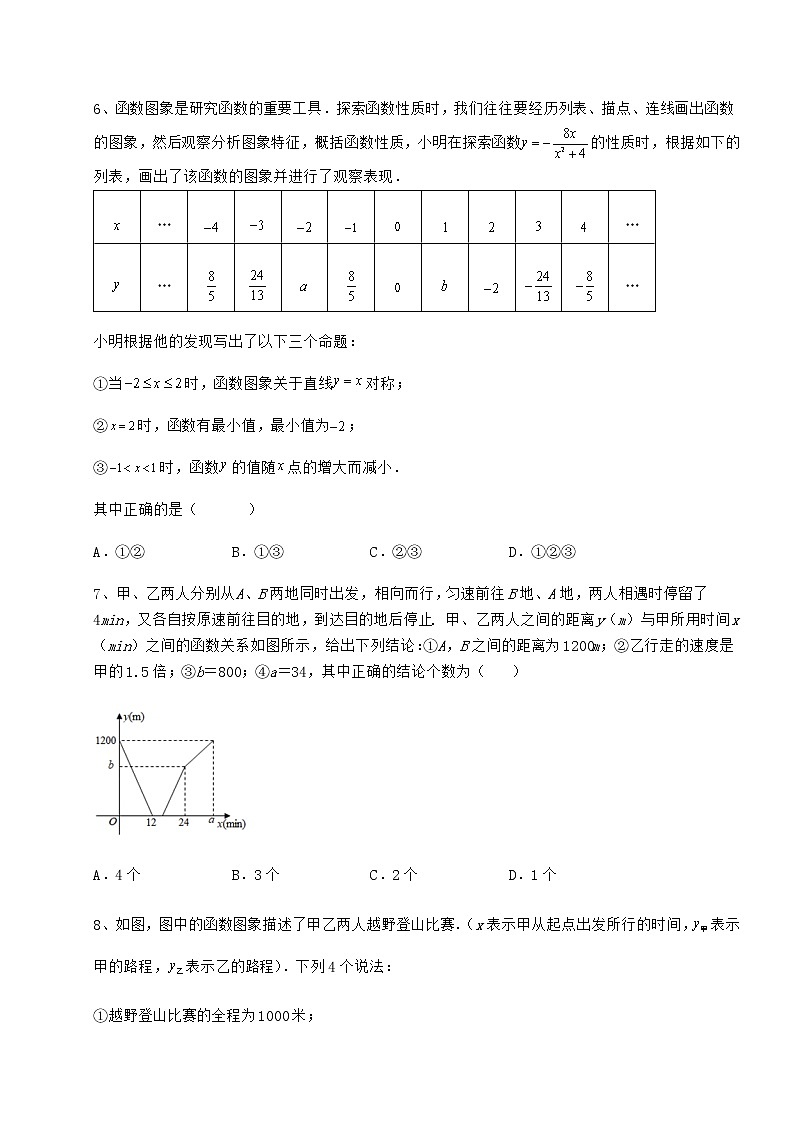
冀教版八年级数学下册第二十章函数专题测试 考试时间：90分钟；命题人：数学教研组考生注意：1、本卷分第I卷（选择题）和第Ⅱ卷（非选择题）两部分，满分100分，考试时间90分钟2、答卷前，考生务必用0.5毫米黑色签字笔将自己的姓名、班级填写在试卷规定位置上3、答案必须写在试卷各个题目指定区域内相应的位置，如需改动，先划掉原来的答案，然后再写上新的答案；不准使用涂改液、胶带纸、修正带，不按以上要求作答的答案无效。第I卷（选择题  30分）一、单选题（10小题，每小题3分，共计30分）1、在平面直角坐标系xOy中, 下列函数的图像过点（-1，1）的是（     ）A． B． C． D．2、今年暑假期间，小东外出爬山．他从山脚爬到山顶的过程中，中途休息了一段时间．设他从山脚出发后所用时间为（分钟），所走的路程为s（米），s与t 之间的函数关系如图所示．下列说法错误的是（       ）A．小明中途休息用了20分钟B．小明休息前爬山的平均速度为每分钟 70米C．小明在上述过程中所走的路程为3800米D．小明休息前爬山的平均速度小于休息后爬山的平均速度3、小江和小北两兄弟步行从家里去公园，小江先出发一段时间后小北再出发，途中小北追上了小江最终先到达公园，两人所走路程s（米）与小北出发后的时间t（分钟）的函数关系如图所示．下列说法正确的是（ ）A．表示的是小江步行的情况，表示的是小北步行的情况B．小江的速度是45米/分钟，小北的速度是60米/分钟C．小江比小北先出发16分钟．D．小北出发后8分钟追上小江4、在函数y=中，自变量x的取值范围是　(　　)A．x>3 B．x≥3 C．x>4 D．x≥3且x≠45、如图1，在矩形ABCD中，AB＜BC，AC，BD交于点O．点E为线段AC上的一个动点，连接DE，BE，过E作EF⊥BD于F．设AE＝x，图1中某条线段的长为y，若表示y与x的函数关系的图象大致如图2所示，则这条线段可能是图1中的（       ）．A．线段EF B．线段DE C．线段CE D．线段BE6、函数图象是研究函数的重要工具．探索函数性质时，我们往往要经历列表、描点、连线画出函数的图象，然后观察分析图象特征，概括函数性质，小明在探索函数的性质时，根据如下的列表，画出了该函数的图象并进行了观察表现．…………小明根据他的发现写出了以下三个命题：①当时，函数图象关于直线对称；②时，函数有最小值，最小值为；③时，函数的值随点的增大而减小．其中正确的是（       ）A．①② B．①③ C．②③ D．①②③7、甲、乙两人分别从A、B两地同时出发，相向而行，匀速前往B地、A地，两人相遇时停留了4min，又各自按原速前往目的地，到达目的地后停止. 甲、乙两人之间的距离y（m）与甲所用时间x（min）之间的函数关系如图所示，给出下列结论：①A，B之间的距离为1200m；②乙行走的速度是甲的1.5倍；③b＝800；④a＝34，其中正确的结论个数为（　　）A．4个 B．3个 C．2个 D．1个8、如图，图中的函数图象描述了甲乙两人越野登山比赛．（x表示甲从起点出发所行的时间，表示甲的路程，表示乙的路程）．下列4个说法：①越野登山比赛的全程为1000米；②甲比乙晚出发40分钟；③甲在途中休息了10分钟；④乙追上甲时，乙跑了750米．其中正确的说法有（       ）个A．1 B．2 C．3 D．49、下列各曲线中，不表示y是x的函数的是（　　）A．  B．C．  D．10、如图，点A的坐标为（0，1），点B是x轴正半轴上的一动点，以AB为边作等腰直角ABC，使∠BAC＝90°，如果点B的横坐标为x，点C的纵坐标为y，那么表示y与x的函数关系的图像大致是（       ）A． B．C． D．第Ⅱ卷（非选择题  70分）二、填空题（5小题，每小题4分，共计20分）1、函数y＝中自变量x的取值范围是______．2、如图1，正方形的边上有一定点，连接．动点从正方形的顶点出发，沿着的方向以2cm/s的速度匀速运动到终点．图2是点运动时，的面积随时间变化的全过程图象，则的长度为______cm．3、已知y＝2x2﹣3x＋1，当x＝1时，函数值为____．4、定义：用_______来表示函数关系的方法叫做解析式法．特点：解析式法简单明了，能够准确的反映整个变化过程中自变量与函数之间的对应关系，但有些实际问题中的函数关系，不能用解析式表示，如气温与时间的函数关系．5、在数学综合实践课中，小明和同学对类似八下教科书25页例2的问题进行拓展探索：如图1，一根长为5米的木棍斜靠在一竖直的墙上，为4米，如果木棍的顶端沿墙下滑米，底端向外移动米，下滑后的木棍记为，则与满足的等式，即关于的函数解析式为，小明利用画图软件画出了该函数图象如图2，（1）请写出图象上点的坐标（1，______）（2）根据图象，当的取值范围为______时，的周长大于的周长．三、解答题（5小题，每小题10分，共计50分）1、长方形的一边长是，其邻边长为，周长是，面积为．（1）写出和之间的关系式（2）写出和之间的关系式（3）当时，等于多少等于多少（4）当增加时，增加多少增加多少2、如图反映的过程是：小明从家出发去菜地浇水，又去玉米地锄草，然后回家．其中x表示时间，y表示小明离他家的距离，小明家，菜地，玉米地在同一直线上．根据图象回答下列问题：（1）菜地离小明家多远？小明走到菜地用了多长时间？小明给菜地浇水用了多长时间？（2）菜地离玉米地多远？小明从菜地到玉米地用了多长时间？（3）小明给玉米地锄草用了多长时间？（4）玉米地离小明家多远？小明从玉米地走回家的平均速度是多少？3、下列各题中分别有几个变量？你能将其中某个变量看成另一个变量的函数吗？若能，请指出自变量的取值范围．（1）（2）在平整的路面上，某型号汽车紧急刹车后仍将滑行，一般地有经验公式，其中表示刹车前汽车的速度（单位：）．（3）在国内投寄到外埠质量为以内的普通信函应付邮资如下表：信件质量邮资/元1.202.403.604.806.00 4、下列各曲线中哪些表示y是x的函数？5、在下列式子中，对于x的每一个确定的值，y有唯一的对应值，即y是x的函数．画出这些函数的图象：（1）；（2）． -参考答案-一、单选题1、D【解析】【分析】利用x=-1时，求函数值进行一一检验是否为1即可【详解】解： 当x=-1时，，图象不过点，选项A不合题意；当x=-1时，，图象不过点，选项B不合题意；当x=-1时，，图象不过点，选项C不合题意；当x=-1时，，图象过点，选项D合题意；故选择：D．【点睛】本题考查求函数值，识别函数经过点，掌握求函数值的方法，点在函数图像上点的坐标满足函数解析式是解题关键．2、D【解析】【分析】根据函数图象可知，小明40分钟爬山2800米，40～60分钟休息，60～100分钟爬山（3800−2800）米，爬山的总路程为3800米，根据路程、速度、时间之间的关系进行解答即可．【详解】解：A、小明中途休息用了60−40＝20分钟，正确，不符合题意；B、小明休息前爬山的速度为2800÷40＝70（米/分钟），正确，不符合题意；C、小明在上述过程中所走的路程为3800米，正确，不符合题意；D、小明休息前爬山的速度为2800÷40＝70（米/分钟），小明休息后爬山的速度是（3800−2800）÷（100−60）＝25（米/分钟），小明休息前爬山的平均速度大于休息后爬山的平均速度，错误，符合题意；故选：D．【点睛】本题考查了函数图象，读懂函数图象，从图象中获取必要的信息是解决本题的关键．3、C【解析】【分析】观察图象，可得：表示的是小北步行的情况，表示的是小江步行的情况，可得A错误；小江32分钟步行（1440-480）米，小北24分钟步行1440米，再根据该时间段内的速度等于路程除以时间，可得B错误；因为小江比小北先走480米，所以用480除以小江的速度30，可得C正确；设小北出发后 分钟追上小江，则 ，解出可得D错误，即可求解．【详解】解：根据题意得：A、因为小江先出发一段时间后小北再出发，所以表示的是小北步行的情况，表示的是小江步行的情况，故本选项不符合题意；B、小江的速度是米/分钟，小北的速度是米/分钟，故本选项不符合题意；C、观察图象，得：小江比小北先出发 分钟，故本选项符合题意；D、设小北出发后 分钟追上小江，则 ，解得： ，即小北出发后16分钟追上小江，故本选项不符合题意；故选：C【点睛】本题主要考查了函数图象的应用，准确从函数图象获取信息是解题的关键．4、D【解析】【分析】根据二次根式的性质和分式的意义，被开方数大于或等于0，分母不等于0，可以求出x的范围．【详解】解：∵x-3≥0，∴x≥3，∵x-4≠0，∴x≠4，综上，x≥3且x≠4，故选：D．【点睛】主要考查了函数自变量的取值范围的确定和分式的意义．函数自变量的范围一般从三个方面考虑：（1）当函数表达式是整式时，自变量可取全体实数；（2）当函数表达式是分式时，考虑分式的分母不能为0；（3）当函数表达式是二次根式时，被开方数为非负数．5、B【解析】【分析】根据各个选项中假设的线段，可以分别由图象得到相应的y随x的变化的趋势，从而可以判断哪个选项是正确的．【详解】解：A、由图1可知，若线段EF是y，则y随x的增大先减小后增大，而由大变小的距离等于由小变大的距离，故此选项不符合题意；B、由图1可知，若线段DE是y，则y随x的增大先减小再增大，而由大变小的距离大于由小变大的距离，在点A的距离是DA，在点C时的距离是DC，DA＞DC，故此选项符合题意；C、由图1可知，若线段CE是y，则y随x的增大越来越小，故此选项不符合题意；D、由图1可知，若线段BE是y，则y随x的增大先减小再增大，而由由大变小的距离小于由小变大的距离，在点A的距离是BA，在点C时的距离是BC，BA＜BC，故此选项不符合题意；故选B．【点睛】本题考查动点问题的函数图象，解题的关键是明确题意，找出所求问题需要的条件，利用数形结合的思想解答问题．6、C【解析】【分析】（1）把，代入 求出、，画出函数图像，函数图象关于直线对称，则横纵坐标交换位置，即可判断①；根据图像可判断②③．【详解】把，代入 得：，画出函数图像如图所示：当时，；当时，，故①错误；由图像可得出：②③正确．故选：C．【点睛】函数的图像与性质，根据表格画函数图像，掌握对称的性质是解题的关键．7、A【解析】【分析】由图象所给信息对结论判断即可．【详解】由图象可知当x=0时，甲、乙两人在A、B两地还未出发故A，B之间的距离为1200m故①正确前12min为甲、乙的速度和行走了1200m故由图象可知乙用了24-4=20min走完了1200m则则故②正确又∵两人相遇时停留了4min∴两人相遇后从16min开始继续行走，由图象x=24时的拐点可知，到24min乙到达目的地则两人相遇后行走了24-16=8min，两人之间的距离为8×100=800米则b=800故③正确从24min开始为甲独自行走1200-800=400m则t=min故a=24+10=34故④正确综上所述①②③④均正确，共有四个结论正确．故选：A．【点睛】本题考查了从函数图象获取信息，运用数形结合的思想是解题的关键．8、C【解析】【分析】根据终点距离起点1000米即可判断①；根据甲、乙图像的起点可以判断②；根据AB段为甲休息的时间即可判断③；设乙需要t分钟追上甲，，求出t即可判断④．【详解】解：由图像可知，从起点到终点的距离为1000米，故①正确；根据图像可知甲出发40分钟之后，乙才出发，故乙比甲晚出发40分钟，故②错误；在AB段时，甲的路程没有增加，即此时甲在休息，休息的时间为40-30=10分钟，故③正确；∵乙从起点到终点的时间为10分钟，∴乙的速度为1000÷10=100米/分钟，设乙需要t分钟追上甲，，解得t=7.5，∴乙追上甲时，乙跑了7.5×100=750米，故④正确；故选C．【点睛】本题主要考查了从函数图像获取信息，解题的关键在于能够准确读懂函数图像．9、D【解析】【分析】根据函数的意义进行判断即可．【详解】解：A、图中，对于的每一个取值，都有唯一确定的值与之对应，选项不符合题意；B、图中，对于的每一个取值，都有唯一确定的值与之对应，选项不符合题意；C、图中，对于的每一个取值，都有唯一确定的值与之对应，选项不符合题意；D、图中，对于的每一个取值，可能有两个值与之对应，选项符合题意．故选：D．【点睛】本题主要考查了函数的定义，解题的关键是掌握函数的定义，在定义中特别要注意，对于的每一个值，都有唯一的值与其对应．10、A【解析】【分析】先作出合适的辅助线，再证明△ADC和△AOB的关系，即可建立y与x的函数关系，从而确定函数图像．【详解】解：由题意可得：OB＝x，OA＝1，∠AOB＝90°，∠BAC＝90°，AB＝AC，点C的纵坐标是y，作AD∥x轴，作CD⊥AD于点D，如图所示：∴∠DAO＋∠AOD＝180°，∴∠DAO＝90°，∴∠OAB＋∠BAD＝∠BAD＋∠DAC＝90°，∴∠OAB＝∠DAC，在△OAB和△DAC中， ∴△OAB≌△DAC（AAS），∴OB＝CD，∴CD＝x，∵点C到x轴的距离为y，点D到x轴的距离等于点A到x的距离1，∴y＝x＋1（x＞0）．故选：A．【点睛】本题考查动点问题的函数图象，明确题意、建立相应的函数关系式是解答本题的关键．二、填空题1、x1且x-3【解析】【分析】根据分母不为0，被开方数大于等于0，进行计算即可．【详解】解：由题意得：1-x0，且x+30，∴x1且x-3，2、2【解析】【分析】点P在点D时，设正方形的边长为a，a×a＝18，解得a＝6；当点P在点C时，×EP×6＝12，解得EP＝4，即EC＝4，进而即可求解．【详解】解：当点P在点D时，由图象可知三角形APE的面积为18，设正方形的边长为a，y＝AB×AD＝a×a＝18，解得a＝6；当点P在点C时，由图象可知三角形APE的面积为12，y＝EP×AB=×EP×6＝12，解得EP＝4，即EC＝4，∴BE＝6-4=2，故答案是：2．【点睛】本题考查的是动点函数图象问题，此类问题关键是弄清楚不同时间段，图象和图形的对应关系．3、0【解析】【分析】根据函数值的求法，直接将x=1代入函数关系式得出即可．【详解】解：y=2x2-3x+1，当x=1时，y=2×12-3×1+1=0．故答案为：0．【点睛】此题主要考查了二次函数图象上点的坐标特征，图象上点的坐标适合解析式是解题关键．4、解析式【解析】略5、          【解析】【分析】（1）把的横坐标代入，求解点的纵坐标即可；（2）先分别求解的周长，的周长，可得：当的周长的周长时，即，再画出直线的图象，直线过点、，观察函数图象可得答案.【详解】解：（1）当时，，故点的坐标为，故答案为1；（2）由，得：，由题意得：，，则的周长，而的周长，则当的周长的周长时，即，由（1）知，当时，，当时，，则在原图象的基础上，画出直线的图象如下，直线过点、，从图象看，当时，，即的周长大于的周长，故答案为：．【点睛】本题考查的是动态问题的函数图象，二次根式的化简，理解图象上点的横坐标与纵坐标的含义，利用两个函数图象的交点坐标解决有关不等关系问题是解题的关键.三、解答题1、（1）；（2）；（3），；（4）当增加时，增加，增加【解析】【分析】（1）根据长方形周长公式进行求解即可；（2）根据长方形面积公式进行求解即可；（3）根据（2）求得的结果把代入先求出x的值，即可求值y的值；（4）把代入（1）（2）中求得的y以及S关于x的表达式中求出变化后的周长和面积，由此求解即可．【详解】解：（1）由长方形的周长公式，得．（2）由长方形的面积公式，得．（3）∵，时，∴，∴．（4）当增加时，，，∵，∴增加，增加．【点睛】本题主要考查了列代数式，整式的加减计算，代数式求值，解一元一次方程，解题的关键在于能够根据题意列出关于周长和面积的代数式．2、（1）菜地离小明家1.1千米，小明从家到菜地用了15分钟，小明给菜地浇水用了10分钟；（2）0.9千米，12分钟；（3）18分钟；（4）2千米，4.8千米/小时【解析】【分析】观察函数图象得到小明用15分钟从家去菜地，浇水用了10分钟，又去离家2千米的玉米地，锄草用了18分钟，然后用了25分钟回家．【详解】解：由图象得：（1）菜地离小明家1.1千米，小明从家到菜地用了15分钟，小明给菜地浇水用了25﹣15＝10（分钟）；（2）菜地离玉米地 2﹣1.1＝0.9（千米），小明从菜地到地用了37﹣25＝12（分钟）；（3）小明给玉米地锄草用了55﹣37＝18（分钟）；（4）玉米地离小明家2千米，小明从玉米地走回家的平均速度＝2÷＝4.8（千米/小时）．【点睛】本题考查函数图象，解答本题的关键是明确题意，利用数形结合的思想解答．3、（1）（2）（3）都含有两个变量；（1）可将温度看成时间（可用字母表示）的函数，时间的取值范围是：；（2）可将看成的函数，的取值范围是：；（3）可将看成的函数，的取值范围是：【解析】【分析】根据函数的定义可知，满足对于x的每一个取值，y都有唯一确定的值与之对应关系，据此即可得出答案，结合图像分析出自变量的取值范围即可；【详解】（1）（2）（3）都含有两个变量；（1）可将温度看成时间（可用字母表示）的函数，时间的取值范围是：；（2）可将看成的函数，的取值范围是：；（3）可将看成的函数，的取值范围是：【点睛】本题主要考查了函数的定义．函数的定义：在一个变化过程中，有两个变量x，y，对于x的每一个取值，y都有唯一确定的值与之对应，则y是x的函数，x叫自变量．4、图（1）（2）（3）中y是x的函数【解析】【分析】设在一个变化过程中有两个变量x与y，对于x的每一个确定的值，y都有唯一的值与其对应，那么就说y是x的函数，x是自变量．由此即可得出结论．【详解】解：图（1）对于自变量x的任何值，y都有唯一的值与之相对应，y是x的函数； 图（2）对于自变量x的任何值，y都有唯一的值与之相对应，y是x的函数； 图（3）对于自变量x的任何值，y都有唯一的值与之相对应，y是x的函数；图（4）对于一部分自变量x的值，y有两个值与之相对应， y不是x的函数；故图（1）（2）（3）中y是x的函数【点睛】本题主要考查了函数概念，关键是掌握注意对函数概念的理解：①有两个变量；②一个变量的数值随着另一个变量的数值的变化而发生变化；③对于自变量的每一个确定的值，函数值有且只有一个值与之对应，即单对应．5、（1）见解析；（2）见解析【解析】【分析】直接利用描点法画出函数图象，即可求解．【详解】解：（1）从式子可以看出，x取任意实数时这个式子都有意义，所以x的取值范围是全体实数．从x的取值范围中选取一些数值，算出y的对应值，列表（计算并填写表中空格）．x…012…y…0.51.52.5… 根据表中数值描点，并用平滑曲线连接这些点（如图）．（2）．列表x…1234…y…6321.5… 根据表中数值描点，并用平滑曲线连接这些点（如图）．【点睛】本题主要考查了描点法画函数图象，熟练掌握描点法画函数图象的基本步骤——列表、描点、连线是解题的关键．