初中数学冀教版八年级下册第二十章 函数综合与测试一课一练

这是一份初中数学冀教版八年级下册第二十章 函数综合与测试一课一练，共23页。试卷主要包含了如图，某汽车离开某城市的距离y等内容，欢迎下载使用。
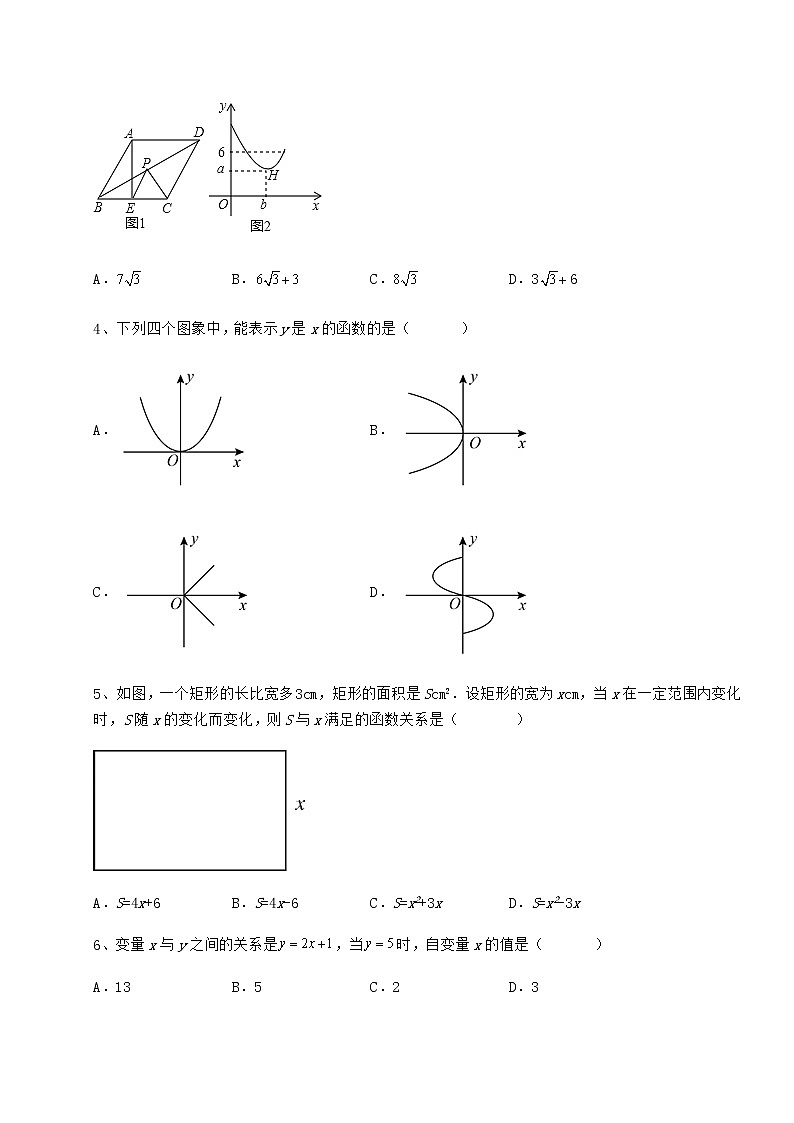
冀教版八年级数学下册第二十章函数专题测试 考试时间：90分钟；命题人：数学教研组考生注意：1、本卷分第I卷（选择题）和第Ⅱ卷（非选择题）两部分，满分100分，考试时间90分钟2、答卷前，考生务必用0.5毫米黑色签字笔将自己的姓名、班级填写在试卷规定位置上3、答案必须写在试卷各个题目指定区域内相应的位置，如需改动，先划掉原来的答案，然后再写上新的答案；不准使用涂改液、胶带纸、修正带，不按以上要求作答的答案无效。第I卷（选择题  30分）一、单选题（10小题，每小题3分，共计30分）1、在函数中，自变量x的取值范围是（　　）A．x≥﹣1 B．x≠3 C．x＞﹣1 D．x≥﹣1且x≠32、下列各曲线中，不表示y是x的函数的是（　　）A．  B．C．  D．3、如图1，在菱形ABCD中，AB＝6，∠BAD＝120°，点E是BC边上的一动点，点P是对角线BD上一动点，设PD的长度为x，PE与PC的长度和为y，图2是y关于x的函数图象，其中H（a，b）是图象上的最低点，则a+b的值为（　　）A． B． C． D．364、下列四个图象中，能表示y是x的函数的是（       ）A． B．C． D．5、如图，一个矩形的长比宽多3cm，矩形的面积是Scm2．设矩形的宽为xcm，当x在一定范围内变化时，S随x的变化而变化，则S与x满足的函数关系是（        ）A．S=4x+6 B．S=4x-6 C．S=x2+3x D．S=x2-3x6、变量x与y之间的关系是，当时，自变量x的值是（       ）A．13 B．5 C．2 D．37、甲、乙两人骑车分别从A、B两地同时出发，沿同一路线匀速骑行，两人先相向而行，甲到达B地后停留20min 再以原速返回A地，当两人到达A地后停止骑行．设甲出发x min后距离A地的路程为y km．图中的折线表示甲在整个骑行过程中y与x的函数关系．在整个骑行过程中，两人只相遇了1次，乙的骑行速度（单位：km/min）可能是（   ）A．0.1 B．0.15 C．0.2 D．0.258、甲、乙二人约好同时出发，沿同一路线去某博物馆参加科普活动，如图，x表示的是行走时间（单位：分），y表示的是甲到出发地的距离（单位：米），最后两人都到达了目的地．根据图中提供的信息，下面有四个结论：①甲、乙二人第一次相遇后，停留了10分钟；②甲先到达目的地；③甲停留10分钟之后提高了行走速度；④甲行走的平均速度要比乙行走的平均速度快．其中正确的是（       ）A．①②④ B．①②③ C．①③④ D．②③④9、如图，某汽车离开某城市的距离y（km）与行驶时间t（h）之间的关系如图所示，根据图形可知，该汽车行驶的速度为（       ）A．30km/h B．60km/h C．70km/h D．90km/h10、小强和爷爷去爬山，爷爷先出发一段时间后小强再出发，途中小强追上了爷爷并最终先爬到山顶，两人所爬的高度h（米）与小强出发后的时间t（分钟）的函数关系如图所示，下列结论正确的是：（       ）A．爷爷比小强先出发20分钟B．小强爬山的速度是爷爷的2倍C．表示的是爷爷爬山的情况，表示的是小强爬山的情况D．山的高度是480米第Ⅱ卷（非选择题  70分）二、填空题（5小题，每小题4分，共计20分）1、已知y＝2x2﹣3x＋1，当x＝1时，函数值为____．2、函数 的定义域是________．3、已知抛物线y=x2﹣x﹣3与x轴的一个交点为（m，0），则代数式2m2﹣2m+2019的值为_____．4、如图，在△ABC中，∠C=90°，BC=8cm，AC=6cm，点E是BC的中点，动点P从A点出发，先以每秒2cm的速度沿A→C运动，然后以1cm/s的速度沿C→B运动．若设点P运动的时间是t秒，那么当t=___________________，△APE的面积等于6．5、一个长方体的底面是一个边长为10cm的正方形，如果高为h(cm)时，体积为V(cm3)，则V与h的关系为_______；三、解答题（5小题，每小题10分，共计50分）1、汽车在发动后的前10秒内以匀加速a=0.8m/s2行驶，这10s内，经过t(s)汽车行驶的路程为s=at2．（1）求t=2.5s和3.5s时，汽车所行驶的路程．（2）汽车在发动后行驶10m，15m所需的时间各为多少? (精确到0.1)2、指出下列问题中的变量和常量：（1）某市的自来水价为4元/t．现要抽取若干户居民调查水费支出情况，记某户月用水量为吨，月应交水费为y元．（2）某地手机通话费为0.2元/．李明在手机话费卡中存入30元，记此后他的手机通话时间为，话费卡中的余额为w元．（3）水中涟漪（圆形水波）不断扩大，记它的半径为r，周长为C，圆周率（圆周长与直径之比）为．（4）把10本书随意放入两个抽昼（每个抽屉内都放），第一个抽屉放入x本，第二个抽屉放入y本．3、下图是某物体的抛射曲线图，其中表示物体与抛射点之间的水平距离，表示物体的高度．（1）这个图象反映了哪两个变量之间的关系？（2）根据图象填表：0123456       （3）当距离取之间的一个确定的值时，相应的高度确定吗？（4）高度可以看成距离的函数吗？4、周六王华骑电动车从家出发去张明家，当他骑了一段路时，想起要帮张明买一本书，于是原路返回到刚经过的新华书店，买到书后继续前往张明家，如图是他离家的路程与时间的关系示意图，请根据图中提供的信息回答下列问题：（1）王华家到张明家的路程是多少米？（2）王华在新华书店停留了多长时间？（3）买到书后，王华从新华书店到张明家骑车的平均速度是多少？（4）本次去张明家途中，王华一共行驶了多少米？5、在初中阶段的函数学习中，我们经历了列表、描点、连线画函数图象，并结合图象研究函数性质的过程．我们对函数图像与性质进行探究，下表是该函数y与自变量x的几组对应值，请解答下列问题：x…0…y…m0n…(1)求该函数的解析式，并写出自变量x的取值范围．(2)表中m的值为         ，n的值为         ．(3)在如图所示的平面直角坐标系中，画出该函数的图像；(4)结合上述研究：①写出方程的解         ．②直接写出关于x的不等式的解集是         ． -参考答案-一、单选题1、D【解析】【分析】根据分式的分母不为零，二次根式被开方数非负即可得到不等式组，解不等式组即可．【详解】由题意得： 解得：且 故选：D【点睛】本题考查了函数有意义的自变量的取值范围，一般地：若解析式中有分式，则分母不为零，若有二次根式，则被开方数非负，其余情况下自变量取值无限制，实际问题要具体情况具体分析．2、D【解析】【分析】根据函数的意义进行判断即可．【详解】解：A、图中，对于的每一个取值，都有唯一确定的值与之对应，选项不符合题意；B、图中，对于的每一个取值，都有唯一确定的值与之对应，选项不符合题意；C、图中，对于的每一个取值，都有唯一确定的值与之对应，选项不符合题意；D、图中，对于的每一个取值，可能有两个值与之对应，选项符合题意．故选：D．【点睛】本题主要考查了函数的定义，解题的关键是掌握函数的定义，在定义中特别要注意，对于的每一个值，都有唯一的值与其对应．3、A【解析】【分析】从图2知，是的最小值，从图1作辅助线知；接下来求出，设与交于点，则求出，，最后得，所以，选．【详解】解：如下图，在边上取点，使得和关于对称，连接，得，连接，作，垂足为，由三角形三边关系和垂线段最短知，，即有最小值，菱形中，，，在△中，，解得，是图象上的最低点，此时令与交于点，由于，在△中，，又，，又的长度为，图2中是图象上的最低点，，又，，故选：A．【点睛】本题考查动点及最小值问题，解题的关键是在于通过翻折点轴对称），然后利用三角形三边关系及垂线段最短原理，判断出最小值为．4、A【解析】【分析】根据“在一个变化过程中，如果有两个变量x、y，并且对于x的每一个确定的值，y都有唯一确定的值与其对应，我们就说x是自变量，y是x的函数”，由此可排除选项．【详解】解：选项A符合函数的概念，而B、C、D都不符合“对于x的每一个确定的值，y都有唯一确定的值与其对应”，故选A．【点睛】本题主要考查函数的定义，熟练掌握函数的定义是解题的关键．5、C【解析】【分析】先用x表示出矩形的长，然后根据矩形的面积公式即可解答.【详解】解：设矩形的宽为xcm，则长为（x+3）cm由题意得：S=x（x+3）=x2+3x.故选C.【点睛】本题主要考查了列函数解析式，用x表示出矩形的长以及掌握矩形的面积公式成为解答本题的关键.6、C【解析】【分析】直接把y=5代入y=2x+1，解方程即可．【详解】解：当y=5时，5=2x+1，解得：x=2，故选：C．【点睛】本题考查了函数值，解题的关键是掌握已知函数解析式，给出函数值时，求相应的自变量的值就是解方程．7、D【解析】【分析】由函数图象可求出甲、乙骑行的时间，根据题意和路程÷时间=速度可求出乙的最小速度即可求解．【详解】解：由函数图象知，A、B两地的距离为25km，甲往返的时间为50+50+20=120（min），∵两人到达A地后停止骑行，且在整个骑行过程中，两人只相遇了1次，∴乙的骑行的速度至少为25÷120= （km/min），∵＞0.2，＜0.25，∴乙的骑行速度可能是0.25km/min，故选：D．【点睛】本题考查一次函数的应用，理解题意，准确从图象中获取有效信息是解答的关键．8、A【解析】【分析】由图象可得：10分钟到20分钟之间，路程没有变化，可判断①，由甲35分钟时到达目的地，乙40分钟到达，可判断②，分别求解前后两段时间内甲的速度可判断③，由前后两段时间内甲的速度都比乙快，可判断④，从而可得答案.【详解】解：①由图象可得：甲、乙二人第一次相遇后，停留了20﹣10＝10（分钟），故①符合题意；②甲在35分时到达，乙在40分时到达，所以甲先到达的目的地，故②符合题意；③甲前面10分钟的速度为：每分钟米，甲在停留10分钟之后的速度为：每分钟米，所以减慢了行走速度，故③不符合题意；④由图象可得：两段路程甲的速度都比乙快，所以甲行走的平均速度要比乙行走的平均速度快，故④符合题意；所以正确的是①②④．故选：A．【点睛】本题考查的是从函数图象中获取信息，理解题意，弄懂图象上点的坐标含义是解本题的关键.9、B【解析】【分析】直接观察图象可得出结果．【详解】解：根据函数图象可知：t=1时，y=90；∵汽车是从距离某城市30km开始行驶的，∴该汽车行驶的速度为90-30=60km/h，故选：B．【点睛】本题主要考查了一次函数的图象，正确的识别图象是解题的关键．10、B【解析】【分析】由爷爷先出发，可以判断C，再根据图象上点的坐标含义分别计算出爷爷与小强的爬山速度，从而可判断A，B，根据图象上点的坐标含义同时可判断D，从而可得答案.【详解】解： 爷爷先出发一段时间后小强再出发，分别表示小强与爷爷的爬山信息，故C不符合题意；由的图象可得：小强爬山的速度为：米/分，由的图象可得：爷爷爬山的速度为：米/分，所以分钟，故A不符合题意；小强爬山的速度是爷爷的2倍，故B符合题意；由图象可得：山的高度是720米，故D不符合题意；故选B【点睛】本题考查的是从函数图象中获取信息，掌握“函数图象上点的坐标含义”是解本题的关键.二、填空题1、0【解析】【分析】根据函数值的求法，直接将x=1代入函数关系式得出即可．【详解】解：y=2x2-3x+1，当x=1时，y=2×12-3×1+1=0．故答案为：0．【点睛】此题主要考查了二次函数图象上点的坐标特征，图象上点的坐标适合解析式是解题关键．2、x≠－1【解析】【分析】根据分母不为零，即可求得定义域．【详解】解：由题意， 即 故答案为：【点睛】本题考查了使函数有意义的自变量的取值范围，即函数的定义域，对于分母中含有未知数的函数解析式，必须考虑其分母不为零．3、2025【解析】【分析】首先把（m，0）代入y=x2-x-3可得m2-m=3，进而可得2m2﹣2m+2019的值．【详解】解：∵抛物线y=x2﹣x﹣3，与x轴的一个交点为（m，0），∴m2-m-3=0，随意m2-m=3，2m2﹣2m+2019=2(m2﹣m)+2019=6+2019=2025．故答案为2025．【点睛】本题考查了二次函数图象上点的坐标特征，根据点在抛物线上得出m2-m-3=0是解题的关键．4、1.5或5或9【解析】【分析】分为两种情况讨论：当点P在AC上时：当点P在BC上时，根据三角形的面积公式建立方程求出其解即可．【详解】如图1，当点P在AC上．∵中，∠C=90°，BC=8cm，AC=6cm，点E是BC的中点，∴CE=4，AP=2t．∵的面积等于6，∴=AP•CE=AP×4=6．∵AP=3，∴t=1.5．如图2，当点P在BC上．则t＞3∵E是DC的中点，∴BE=CE=4．∴=EP•AC=EP×6=6， ∴PE=2，∴t=5或t=9．总上所述，当t=1.5或5或9时，的面积会等于6．故答案为：1.5或5或9．【点睛】本题考查了直角三角形的性质的运用，三角形的面积公式的运用，解答时灵活运用三角形的面积公式求解是关键．5、V=100h【解析】【分析】根据体积公式：体积=底面积×高进行填空即可．【详解】解：V与h的关系为V=100h；故答案为：V=100h．【点睛】本题主要考查了列函数关系式，题目比较简单．三、解答题1、（1）2.5，4.9；（2）5，6.1【解析】【分析】(1)根据公式，得函数解析式，根据自变量的值，得函数值．(2)根据函数值，得相应的自变量的值．【详解】(1)∵s=at2，∴s=×0.8t2=t2．当t=2.5时，s=×2.52=2.5(m)，当t=3.5时，s=×3.52=4.9(m)．(2)当s=10时， t2=10，解得t=5(s)，当s=15时， t2=15，解得t≈6.1(s)．【点睛】本题考查了函数值，利用了函数的自变量与函数值的对应关系．2、（1）变量x，y；常量4．（2）变量t，w；常量0.2，30．（3）变量r，C；常量．（4）变量x，y；常量10．【解析】【分析】根据常量与变量的定义求解即可．【详解】解：(1)由题意可知，变量为x，y，常量为4；(2)由题意可知，变量为t，w，常量为0.2，30；(3)由题意可知，变量为r，C，常量为；(4)由题意可知，变量为x，y，常量为10．【点睛】本题考查常量与变量的定义，常量是指在变化过程中不随时间变化的量；变量是指在变化过程中随着时间变化的量．3、（1）反映了拋射距离与高度之间的关系；（2）2.0，2.5，2.65，2.5，2.0，1.2，0；（3）确定；（4）可以【解析】【分析】（1）根据变量的定义，即可求解；（2）根据图象填表即可；（3）根据这一范围内对于任一个距离，对应的函数值高度是唯一的，即可得到相应的高度是确定的；（4）根据函数的定义，即可求解．【详解】解：（1）根据题意得：这个图象反映了高度与拋射水平距离之间的关系；（2）根据图象填表如下：01234562.02.52.652.52.01.20 （3）当距离取之间的一个确定的值时，相应的高度是确定的，理由如下：因为这一范围内对于任一个距离，对应的函数值高度是唯一的，所以相应的高度是确定的；（4）∵高度随距离的变化而变化，并且对于任一个距离，对应的函数值高度是唯一的，∴高度可以看成距离的函数．【点睛】本题主要考查了函数与变量，熟练掌握设在一个变化过程中有两个变量x与y，对于x的每一个确定的值，y都有唯一的值与其对应，那么就说y是x的函数，x是自变量是解题的关键．4、（1）4800米；（2）8分钟；（3）450米/分；（4）6800米【解析】【分析】（1）根据函数图象，直接可得王华家到张明家的路程；（2）根据函数图像平行于横轴的部分即为停留的时间，据此可得王华在新华书店停留了多长时间；（3）根据函数图象求得路程和时间，概念速度等于路程除以时间即可求得；（4）根据函数图象可得路程为3段，将其相加即可．【详解】解：（1）根据函数图象，可知王华家到张明家的路程是4800米；（2）24﹣16＝8（分钟）．所以王华在新华书店停留了8分钟；（3）王华从新华书店到张明家的路程为4800﹣3000＝1800米，所用时间为28﹣24＝4分钟，小王华从新华书店到张明家骑车的平均速度是：1800÷4＝450（米/分）；（4）根据函数图象，王华一共行驶了4800＋2×（4000﹣3000）＝6800（米）．【点睛】本题考查了函数图象，要理解横纵坐标表示的含义以及王华的运动过程，从函数图象中获取信息是解题的关键．5、 (1)，自变量取任意实数(2)，(3)见解析(4)①；②或【解析】【分析】（1）选择两组数据代入函数得到一个二元一次方程，解出a，b即可求出解析式；（2）根据（1）得到的解析式代入m，n对应的x即可；（3）描点法标记好每个点，再用光滑的曲线连接各点即可得到函数图像．【详解】解：（1）由表格得，，在函数上，将，代入，得：，解得：，该函数解析式为：，自变量取任意实数；（2）当时，，即，当时，，即，故答案为：，；（3）图象如图(4)由图象可知，方程的解为不等式的解集为：，故答案是：，．【点睛】本题考查新函数解析式的求法、根据自变量求因变量、函数图像的绘制，掌握这些是本题关键．