中考数学一轮全程复习课时练第45课时《实验操作型问题》(教师版)

这是一份中考数学一轮全程复习课时练第45课时《实验操作型问题》(教师版)，共7页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。


一、选择题
1．如图，小明家的住房平面图呈长方形，被分割成3个正方形和2个长方形后仍是中心对称图形．若只知道原住房平面图长方形的周长，则分割后不用测量就能知道周长的图形的标号为 (A)
A．①② B．②③
C．①③ D．①②③
二、填空题
2．把标准纸一次又一次对开，可以得到均相似的“开纸”．现在我们在长为2eq \r(2)，宽为1的矩形纸片中，画两个小矩形，使这两个小矩形的每条边都与原矩形的边平行，或小矩形的边在原矩形纸的边上，且每个小矩形均与原矩形纸相似，然后将它们剪下，则所剪得的两个小矩形纸片周长之和的最大值是__eq \f(15,4)＋4eq \r(2)__.
【解析】∵在长为2eq \r(2)，宽为1的矩形纸片中，画两个小矩形，使这两个小矩形的每条边都与原矩形纸的边平行，或小矩形的边在原矩形的边上，且每个小矩形均与原矩形纸相似，
∴要使所剪得的两个小矩形纸片周长之和最大，则这两个小矩形纸片长与宽的和最大．∵矩形的长与宽之比为2eq \r(2)∶1，
∴剪得的两个小矩形中，一个矩形的长为1，宽为eq \f(1×1,2\r(2))＝eq \f(\r(2),4)，
∴另外一个矩形的长为2eq \r(2)－eq \f(\r(2),4)＝eq \f(7\r(2),4)，宽为eq \f(\f(7\r(2),4)×1,2\r(2))＝eq \f(7,8)，
∴所剪得的两个小矩形纸片周长之和的最大值是2eq \b\lc\(\rc\)(\a\vs4\al\c1(1＋\f(\r(2),4)＋\f(7\r(2),4)＋\f(7,8)))＝4eq \r(2)＋eq \f(15,4).
三、解答题
3．如图，矩形纸片ABCD，将△AMP和△BPQ分别沿PM和PQ折叠(AP＞AM)，点A和点B都与点E重合；再将△CQD沿DQ折叠，点C落在线段EQ上点F处．
(1)判断△AMP，△BPQ，△CQD和△FDM中有哪几对相似三角形？(不需说明理由)
(2)如果AM＝1，sin∠DMF＝eq \f(3,5)，求AB的长．
解：(1)△AMP∽△BPQ∽△CQD，
∵四边形ABCD是矩形，
∴∠A＝∠B＝∠C＝90°，
根据折叠的性质可知：
∠APM＝∠EPM，∠EPQ＝∠BPQ，
∴∠APM＋∠BPQ＝∠EPM＋∠EPQ＝90°，
∵∠APM＋∠AMP＝90°，
∴∠BPQ＝∠AMP，
∴△AMP∽△BPQ，
同理：△BPQ∽△CQD，
根据相似的传递性，△AMP∽△CQD；
(2)∵AD∥BC，
∴∠DQC＝∠MDQ，
根据折叠的性质可知：∠DQC＝∠DQM，
∴∠MDQ＝∠DQM，∴MD＝MQ，
∵AM＝ME，BQ＝EQ，
∴BQ＝MQ－ME＝MD－AM，
∵sin∠DMF＝eq \f(DF,MD)＝eq \f(3,5)，
∴设DF＝3x，MD＝5x，
∴BP＝PA＝PE＝eq \f(3x,2)，BQ＝5x－1，
∵△AMP∽△BPQ，
∴eq \f(AM,BP)＝eq \f(AP,BQ)，∴eq \f(1,\f(3x,2))＝eq \f(\f(3x,2),5x－1)，解得x＝eq \f(2,9)或x＝2，
又∵AP>AM，∴x＝eq \f(2,9)时，AP＝eq \f(1,3)∴AB＝6.
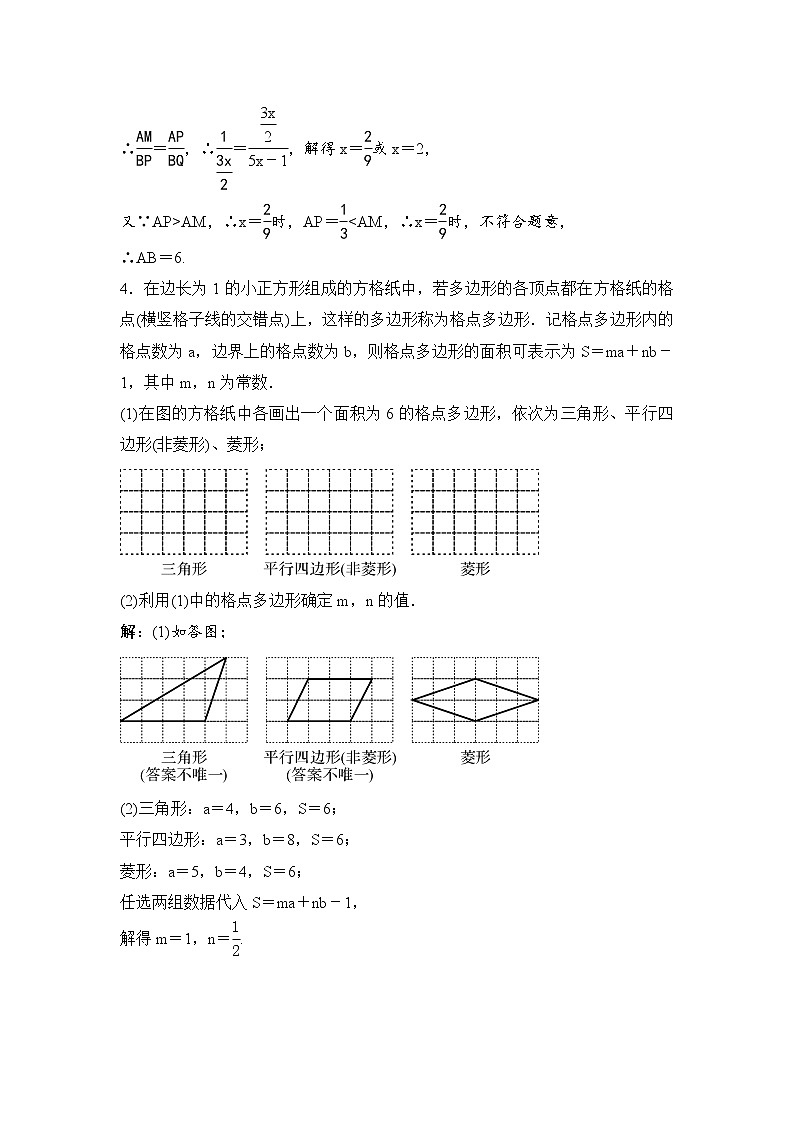
4．在边长为1的小正方形组成的方格纸中，若多边形的各顶点都在方格纸的格点(横竖格子线的交错点)上，这样的多边形称为格点多边形．记格点多边形内的格点数为a，边界上的格点数为b，则格点多边形的面积可表示为S＝ma＋nb－1，其中m，n为常数．
(1)在图的方格纸中各画出一个面积为6的格点多边形，依次为三角形、平行四边形(非菱形)、菱形；
(2)利用(1)中的格点多边形确定m，n的值．
解：(1)如答图；
(2)三角形：a＝4，b＝6，S＝6；
平行四边形：a＝3，b＝8，S＝6；
菱形：a＝5，b＝4，S＝6；
任选两组数据代入S＝ma＋nb－1，
解得m＝1，n＝eq \f(1,2).
5．提出问题：
(1)如图①，在等边△ABC中，点M是BC上的任意一点(不含端点B，C)，连结AM，以AM为边作等边△AMN，连结CN.求证：∠ABC＝∠ACN；
类比探究
(2)如图②，在等边△ABC中，点M是BC延长线上的任意一点(不含端点C)，其他条件不变，(1)中结论∠ABC＝∠ACN还成立吗？请说明理由；
拓展延伸
(3)如图③，在等腰△ABC中，BA＝BC，点M是BC上的任意一点(不含端点B，C)，连结AM，以AM为边作等腰△AMN，使顶角∠AMN＝∠ABC.连结CN.试探究∠ABC与∠ACN的数量关系，并说明理由．
解：(1)证明：∵△ABC，△AMN是等边三角形，
∴AB＝AC，AM＝AN，∠BAC＝∠MAN＝60°，
∴∠BAM＝∠CAN，∴△BAM≌△CAN(SAS)，
∴∠ABC＝∠ACN；
(2)结论∠ABC＝∠ACN仍成立．
理由：∵△ABC，△AMN是等边三角形，
∴AB＝AC，AM＝AN，∠BAC＝∠MAN＝60°.
∴∠BAM＝∠CAN.∴△BAM≌△CAN；
∴∠ABC＝∠ACN；
(3)∠ABC＝∠ACN.
理由：∵BA＝BC，MA＝MN，∠ABC＝∠AMN，
∴∠BAC＝∠MAN，∴△ABC∽△AMN，
∴eq \f(AB,AM)＝eq \f(AC,AN).∵∠BAM＝∠BAC－∠MAC，∠CAN＝∠MAN－∠MAC，
∴∠BAM＝∠CAN，
∴△BAM∽△CAN，∴∠ABC＝∠ACN.
6．如图，点P是正方形ABCD内一点，点P到点A，B和D的距离分别为1，2eq \r(2)，eq \r(10).△ADP沿点A旋转至△ABP′，连结PP′，并延长AP与BC相交于点Q.
(1)求证：△APP′是等腰直角三角形；
(2)求∠BPQ的大小；
(3)求CQ的长．

解：(1)证明：因为△ABP′是由△ABP顺时针旋转90°得到，
则AP＝AP′，∠PAP′＝90°，
∴△APP′是等腰直角三角形；
(2)∵△APP′是等腰直角三角形，
∴∠APP′＝45°，PP′＝eq \r(2)，
又∵BP′＝eq \r(10)，BP＝2eq \r(2)，
∴PP′2＋BP2＝BP′2，
∴∠BPP′＝90°，
∵∠APP′＝45°，
∴∠BPQ＝180°－∠APP′－∠BPP′＝45°；
(3)过点B作BE⊥AQ于点E，则△PBE为等腰直角三角形，
∴BE＝PE，BE2＋PE2＝PB2，
∴BE＝PE＝2，∴AE＝3，
∴AB＝eq \r(AE2＋BE2)＝eq \r(13)，则BC＝eq \r(13)，
∵∠BAQ＝∠EAB，∠AEB＝∠ABQ＝90°，
∴△ABE∽△AQB，
∴eq \f(AE,AB)＝eq \f(AB,AQ)，即eq \f(3,\r(13))＝eq \f(\r(13),AQ)，∴AQ＝eq \f(13,3)，
∴BQ＝eq \r(AQ2－AB2)＝eq \f(2,3)eq \r(13)，
∴CQ＝BC－BQ＝eq \f(\r(13),3).
7．如图①，在△ABC中，∠ACB＝90°，AC＝4 cm，BC＝3 cm，如果点P由点B出发沿BA的方向向点A匀速运动，同时点Q由点A出发沿AC方向向点C匀速运动，它们速度均是1 cm/s，连结PQ，设运动时间为t(s)(0(1)设△APQ的面积为S，当t为何值时，S取得最大值？S的最大值是多少？
(2)如图②，连结PC，将△PQC沿QC翻折，得到四边形PQP′C，当四边形PQP′C为菱形时，求t的值；
(3)当t为何值时，△APQ是等腰三角形？
解：(1)由勾股定理，得AB＝5；
由题意得BP＝AQ＝t，AP＝5－t.
如答图①过点P作PD⊥AC于点D，则△APD∽△ABC，
∴eq \f(PD,3)＝eq \f(5－t,5)，解得PD＝3－eq \f(3,5)t，∴S＝eq \f(1,2)teq \b\lc\(\rc\)(\a\vs4\al\c1(3－\f(3,5)t))＝－eq \f(3,10)eq \b\lc\(\rc\)(\a\vs4\al\c1(t－\f(5,2)))eq \s\up12(2)＋eq \f(15,8)，
∴当t＝eq \f(5,2)时，S取得最大值是eq \f(15,8)；

(2)连结PP′交AC于点D，
∵PQP′C是菱形，∴PP′与QC互相垂直平分，
∴AD＝t＋eq \f(4－t,2)＝eq \f(t,2)＋2，PD＝3－eq \f(3,5)t，AP＝5－t.
由勾股定理得eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(t,2)＋2))eq \s\up12(2)＋eq \b\lc\(\rc\)(\a\vs4\al\c1(3－\f(3,5)t))eq \s\up12(2)＝(5－t)2，解得t1＝eq \f(20,13)，t2＝20(舍去)；

(3)△APQ是等腰三角形，
①当AP＝AQ时，t＝5－t，则t＝eq \f(5,2)；
②当PA＝PQ时，如答图③，作PE⊥AC于E，
∵cs∠A＝eq \f(4,5)，则AE＝eq \f(4,5)(5－t)，
又∵AP＝PQ，∴AE＝eq \f(1,2)AQ＝eq \f(t,2)，∴eq \f(4,5)(5－t)＝eq \f(t,2)，∴t＝eq \f(40,13)；
③当QA＝QP时，如答图④，作QF⊥AB于点F，
∴AF＝eq \f(4,5)t；∴eq \f(8,5)t＝5－t，∴t＝eq \f(25,13).
综上所述，当t＝eq \f(5,2)或t＝eq \f(25,13)或t＝eq \f(40,13)时，△APQ是等腰三角形．