2022届高考数学理一轮复习新人教版课件：第八章平面解析几何第九节第1课时最值范围证明问题

这是一份2022届高考数学理一轮复习新人教版课件：第八章平面解析几何第九节第1课时最值范围证明问题，共60页。PPT课件主要包含了无公共点，一个交点，不相等，两个交点，无交点，答案6等内容，欢迎下载使用。

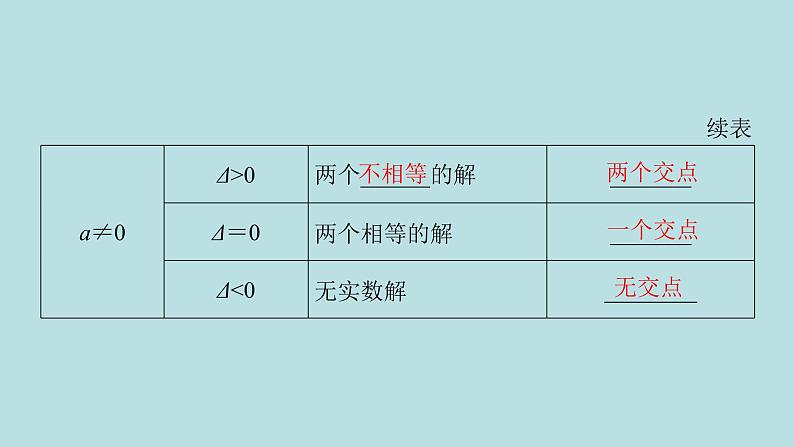
1．直线与圆锥曲线的位置关系的判定代数法：把圆锥曲线方程C与直线方程l联立消去y，整理得到关于x的方程ax2＋bx＋c＝0.
直线与圆锥曲线相交与相切的区别与联系(1)直线与椭圆相交⇔有两个交点；相切⇔有一个公共点．(2)直线与双曲线相交时，可以为一个公共点，即直线与渐近线平行；可以为两个公共点，直线与渐近线不平行．直线与双曲线相切时，只有一个公共点．(3)直线与抛物线相交，当直线平行对称轴时，只有一个公共点；当直线与对称轴不平行，有两个公共点．直线与抛物线相切时，只有一个公共点．
3．(基本应用：椭圆的焦点三角形)已知F1，F2是椭圆16x2＋25y2＝1 600的两个焦点，P是椭圆上一点，且PF1⊥PF2，则△F1PF2的面积为________________．答案：64
5．(基本能力：抛物线的性质与圆的切线)已知抛物线C的方程为y2＝2px(p＞0)，⊙M的方程为x2＋y2＋8x＋12＝0，如果抛物线C的准线与⊙M相切，那么p的值为____________________．答案：12或4
第一课时　最值、范围、证明问题
(2)(2020·辽宁沈阳检测)已知抛物线y2＝4x的一条弦AB恰好以P(1，1)为中点，则弦AB所在直线的方程是________________．
答案：2x－y－1＝0
[典例剖析][典例]　如图所示，已知点F为抛物线E：y2＝2px(p>0)的焦点，点A(2，m)在抛物线E上，且|AF|＝3.(1)求抛物线E的方程；(2)已知点G(－1，0)，延长AF交抛物线E于点B，证明：以点F为圆心且与直线GA相切的圆，必与直线GB相切．
方法总结圆锥曲线中证明问题的类型及解题策略(1)圆锥曲线中的证明问题，主要有两类：一是证明点、直线、曲线等几何元素中的位置关系，如：某点在某直线上、某直线经过某个点、某两条直线平行或垂直等；二是证明直线与圆锥曲线中的一些数量关系(相等或不等).
(2)解决证明问题时，主要根据直线、圆锥曲线的性质、直线与圆锥曲线的位置关系等，通过相关的性质应用、代数式的恒等变形以及必要的数值计算等进行证明．
方法总结1．解决圆锥曲线中的取值范围问题的5种常用解法(1)利用圆锥曲线的几何性质或判别式构造不等关系，从而确定参数的取值范围．(2)利用已知参数的范围，求新参数的范围，解这类问题的核心是建立两个参数之间的等量关系．
(3)利用隐含的不等关系建立不等式，从而求出参数的取值范围．(4)利用已知的不等关系构造不等式，从而求出参数的取值范围．(5)利用求函数的值域的方法将待求量表示为其他变量的函数，求其值域，从而确定参数的取值范围．
2．处理圆锥曲线最值问题的求解方法圆锥曲线中的最值问题类型较多，解法灵活多变，但总体上主要有两种方法：一是利用几何法，即通过利用曲线的定义、几何性质以及平面几何中的定理、性质等进行求解；二是利用代数法，即把要求最值的几何量或代数解析式表示为某个(些)参数的函数(解析式)，然后利用函数方法、不等式方法等进行求解．　　
(2020·南昌模拟)已知抛物线C：x2＝2py(p＞0)和定点M(0，1)，设过点M的动直线交抛物线C于A，B两点，抛物线C在A，B处的切线的交点为N.(1)若N在以AB为直径的圆上，求p的值；(2)若△ABN的面积的最小值为4，求抛物线C的方程．