河南省信阳市2021届高三第二次教学质量检测理科数学试卷含答案

这是一份河南省信阳市2021届高三第二次教学质量检测理科数学试卷含答案，共10页。试卷主要包含了保持卡面清洁，不折叠，不破损，如图是函数f的解析式可能是，“lnx＞lny”是“＜”的等内容，欢迎下载使用。
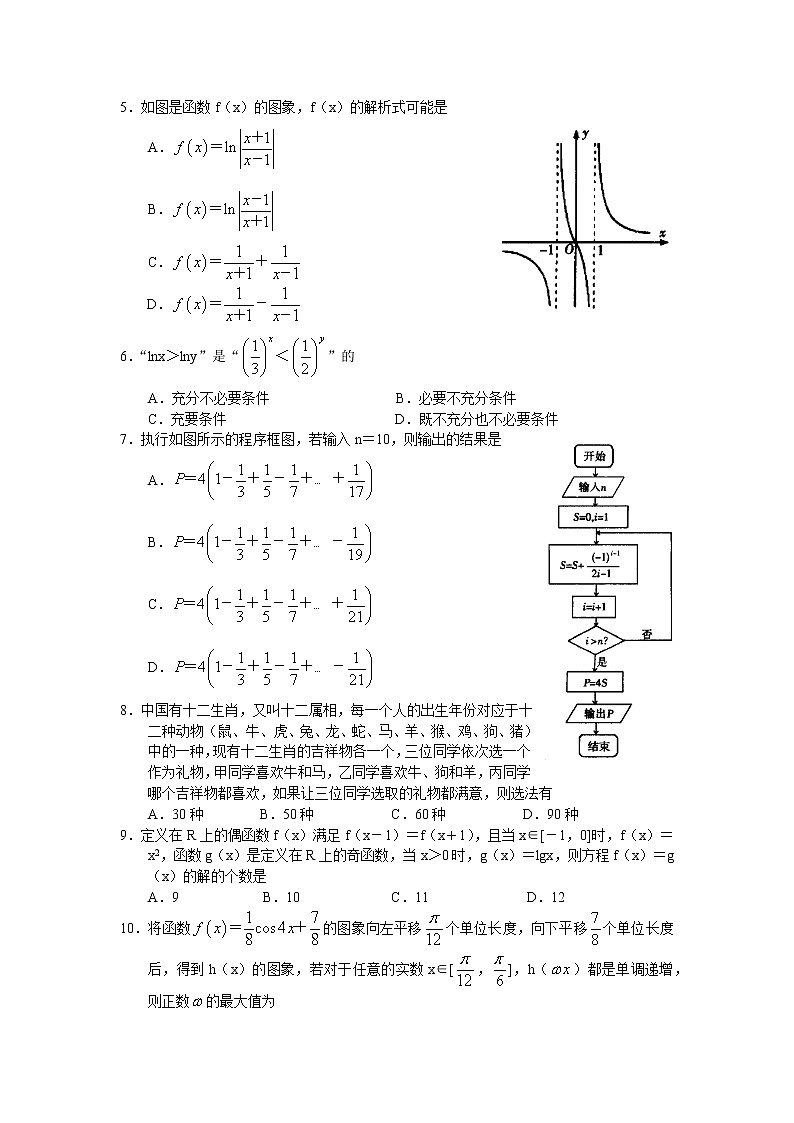
 信阳市2020—2021学年普通高中高三第二次教学质量检测数学（理科）    本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分。考生作答时，将答案答在答题卡上，在本试卷上答题无效。考试结束后，将本试卷和答题卡一并交回。注意事项：    1．答题前，考生务必将本人的姓名、准考证号等考生信息填写在答题卡上，并用2B铅笔将准考证号填涂在相应位置。    2．选择题答案使用2B铅笔填涂，如需改动，用橡皮擦干净后，再选涂其他答案标号；非选择题答案使用0．5毫米的黑色墨水签字笔书写，字体工整、笔迹清楚。    3．请按照题号在各题的答题区域（黑色线框）内作答，超出答题区域书写的答案无效。    4．保持卡面清洁，不折叠，不破损。第Ⅰ卷一、选择题：本大题共12个小题，每小题5分，共60分，在每小题给出的四个选项中，只有一项是符合题目要求的．1．已知集合A＝{x｜x2－6x＋5≤0}，B＝{｜}，A∩B等于    A．[1，＋∞）   B．[1，3]          C．（3，5]          D．[3，5]2．已知复数z＝i＋i2020．则｜z｜等于    A．         B．1               C．0              D．23．已知某地区中小学生人数和近视情况分别如图甲和图乙所示．为了了解该地区中小学生的近视形成原因用分层抽样的方法抽取2％的学生进行调查，则样本容量和抽取的高中生近视人数分别为    A．100，40      B．100，20        C．200，40         D．200，204．已知正项数列{}满足，{}的前项和为，则等于A．          B．            C．            D．    5．如图是函数f（x）的图象，f（x）的解析式可能是    A．    B．    C．D．6．“lnx＞lny”是“＜”的    A．充分不必要条件                  B．必要不充分条件    C．充要条件                        D．既不充分也不必要条件7．执行如图所示的程序框图，若输入n＝10，则输出的结果是    A．    B．    C．    D．8．中国有十二生肖，又叫十二属相，每一个人的出生年份对应于十二种动物（鼠、牛、虎、兔、龙、蛇、马、羊、猴、鸡、狗、猪）中的一种，现有十二生肖的吉祥物各一个，三位同学依次选一个作为礼物，甲同学喜欢牛和马，乙同学喜欢牛、狗和羊，丙同学哪个吉祥物都喜欢，如果让三位同学选取的礼物都满意，则选法有    A．30种        B．50种           C．60种           D．90种9．定义在R上的偶函数f（x）满足f（x－1）＝f（x＋1），且当x∈[－1，0]时，f（x）＝x2，函数g（x）是定义在R上的奇函数，当x＞0时，g（x）＝lgx，则方程f（x）＝g（x）的解的个数是    A．9            B．10             C．11              D．1210．将函数的图象向左平移个单位长度，向下平移个单位长度后，得到h（x）的图象，若对于任意的实数x∈[，]，h（）都是单调递增，则正数的最大值为    A．2            B．             C．              D．11．如图，F1、F2是双曲线C：（a＞0，b＞0）的左、右焦点，过F2的直线与双曲线C交于A、B两点．若｜AB｜：｜BF1｜：｜AF1｜＝3：4：5，则该双曲线的渐近线方程为    A．    B．    C．D．12．已知函数，k∈[1，＋∞），曲线y＝f（x）上总存在两点M（x1，y1），N（x2，y2）使曲线y＝f（x）在M、N两点处的切线互相平行，则x1＋x2的取值范围为A．[4，＋∞）   B．（4，＋∞）      C．[，＋∞）    D．（，＋∞） 第Ⅱ卷二、填空题：本大题共4个小题，每小题5分，共20分，把答案填在答题卡的相应位置．13．已知x，y满足约束条件，则的最大值为___________．14．在（x2－2x－3）3的展开式中，含x2的项的系数是___________．15．已知抛物线y2＝4x的焦点为F，过点F的直线交抛物线于A、B两点，且｜FA｜·｜FB｜＝6，则｜AB｜＝___________． 16．在△ABC中，向量＝（，cosx），＝（cos，sinx），则△ABC面积的最大值是___________．三、解答题：本大题共6小题，共70分，解答应写出文字说明、证明过程或演算步骤．17．（本小题12分）在△ABC中，a、b、c分别是角A、B、C的对边，且（a＋b＋c）（a＋b－c）＝3ab．   （Ⅰ）求角C的值；   （Ⅱ）若c＝2，且△ABC为锐角三角形，求a＋b的取值范围． 18．（本小题12分）已知等比数列{}的前项和为（≠），满足，，－成等差数列，且＝．   （Ⅰ）求数列{}的通项公式；   （Ⅱ）设，求数列{}的前项和． 19．（本小题12分）2020年信阳市为了进一步深化“平安校园”创建活动，加强校园安全教育宣传，某高中对该校学生进行了安全教育知识测试（满分100分），并从中随机抽取了200名学生的成绩，经过数据分析得到如图1所示的频数分布表，并绘制了得分在[30，40）以及[90，100]的茎叶图，分别如图2、3所示．   （Ⅰ）求这200名同学得分的平均数；（同组数据用区间中点值作代表）   （Ⅱ）如果变量X满足P（－＜X＜＋）＞0．9544且P（－＜X＜＋）＞0．9974，则称变量X“近似满足正态分布N（，）的概率分布”．经计算知样本方差为210，现在取和分别为样本平均数和方差，以样本估计总体，将频率视为概率，如果该校学生的得分“近似满足正态分布N（，）的概率分布”，则认为该校的校园安全教育是成功的，否则视为不成功．试判断该校的安全教育是否成功，并说明理由．   （Ⅲ）学校决定对90分及以上的同学进行奖励，为了体现趣味性，采用抽奖的方式进行，其中得分不低于94的同学有两次抽奖机会，低于94的同学只有一次抽奖机会，每次抽奖的奖金及对应的概率分别为：现在从不低于90分的同学中随机选一名同学，记其获奖金额为ξ，以样本估计总体，将频率视为概率，求ξ的分布列和数学期望．   （参考数据：≈14．5） 20．（本小题12分）已知椭圆N：（a＞b＞0）经过点C（0，1）且离心率为．   （Ⅰ）求椭圆N的标准方程与焦距；   （Ⅱ）直线l：与椭圆N的交点为A，B两点，线段AB的中点为M．是否存在常数，使∠AMC＝恒成立，并说明理由． 21．（本小题12分）已知函数f（x）＝ex－2ax－a，g（x）＝lnx   （Ⅰ）讨论f（x）的单调性；   （Ⅱ）用max{m，n}表示m，n中的最大值，若函数h（x）＝max{f（x），g（x）}（x＞0）只有一个零点，求a的取值范围． 请考生在22，23题中任选一题作答，如果多做，则按所做第一题计分。22．（本小题10分）已知直线l的参数方程为（t为参数），以坐标原点为极点，x正半轴为极轴，建立极坐标系，曲线C的极坐标方程是．   （Ⅰ）写出直线l的极坐标方程与曲线C的直角坐标方程；   （Ⅱ）若点P是曲线C上的动点，求点P到直线l距离的最小值，并求出此时P点坐标．  23．（本小题10分）设函数f（x）＝｜x＋2｜－｜x－2｜   （Ⅰ）解不等式f（x）≥2；   （Ⅱ）当x∈R，0＜t＜1时，证明：｜x＋2｜－｜x－2｜≤．