沪教版 (五四制)第十三章 相交线 平行线综合与测试同步达标检测题

这是一份沪教版 (五四制)第十三章 相交线 平行线综合与测试同步达标检测题，共29页。试卷主要包含了如图，下列四个结论，如图，能与构成同位角的有，如图，不能推出a∥b的条件是等内容，欢迎下载使用。
七年级数学第二学期第十三章相交线 平行线章节测评
考试时间：90分钟；命题人：数学教研组
考生注意：
1、本卷分第I卷（选择题）和第Ⅱ卷（非选择题）两部分，满分100分，考试时间90分钟
2、答卷前，考生务必用0.5毫米黑色签字笔将自己的姓名、班级填写在试卷规定位置上
3、答案必须写在试卷各个题目指定区域内相应的位置，如需改动，先划掉原来的答案，然后再写上新的答案；不准使用涂改液、胶带纸、修正带，不按以上要求作答的答案无效。
第I卷（选择题 30分）
一、单选题（10小题，每小题3分，共计30分）
1、一把直尺与一块直角三角板按如图方式摆放，若∠1＝28°，则∠2＝（　　）

A．62° B．58° C．52° D．48°
2、直线、、、如图所示．若∠1=∠2，则下列结论错误的是（ ）

A．ABCD B．∠EFB=∠3 C．∠4=∠5 D．∠3=∠5
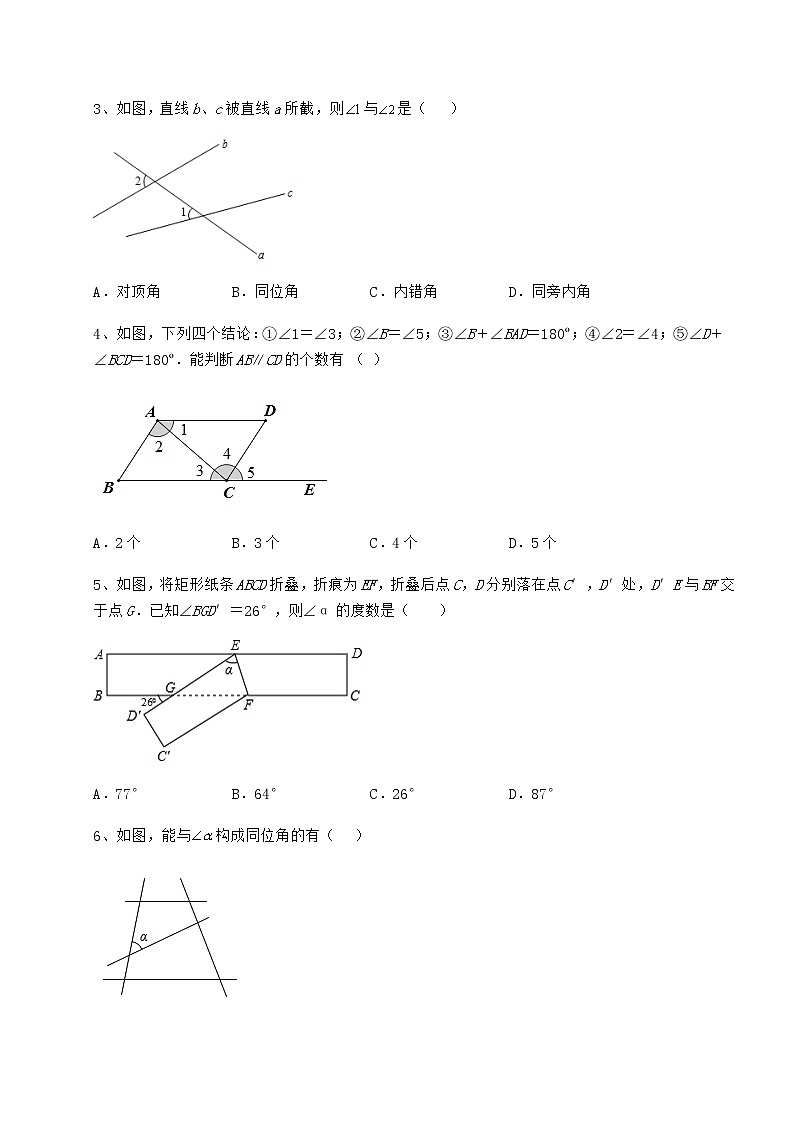
3、如图，直线b、c被直线a所截，则与是（ ）

A．对顶角 B．同位角 C．内错角 D．同旁内角
4、如图，下列四个结论：①∠1＝∠3；②∠B＝∠5；③∠B＋∠BAD＝180º；④∠2＝∠4；⑤∠D＋∠BCD＝180º．能判断AB∥CD的个数有 （ ）

A．2个 B．3个 C．4个 D．5个
5、如图，将矩形纸条ABCD折叠，折痕为EF，折叠后点C，D分别落在点C′，D′处，D′E与BF交于点G．已知∠BGD′＝26°，则∠α的度数是（ ）

A．77° B．64° C．26° D．87°
6、如图，能与构成同位角的有（ ）

A．4个 B．3个 C．2个 D．1个
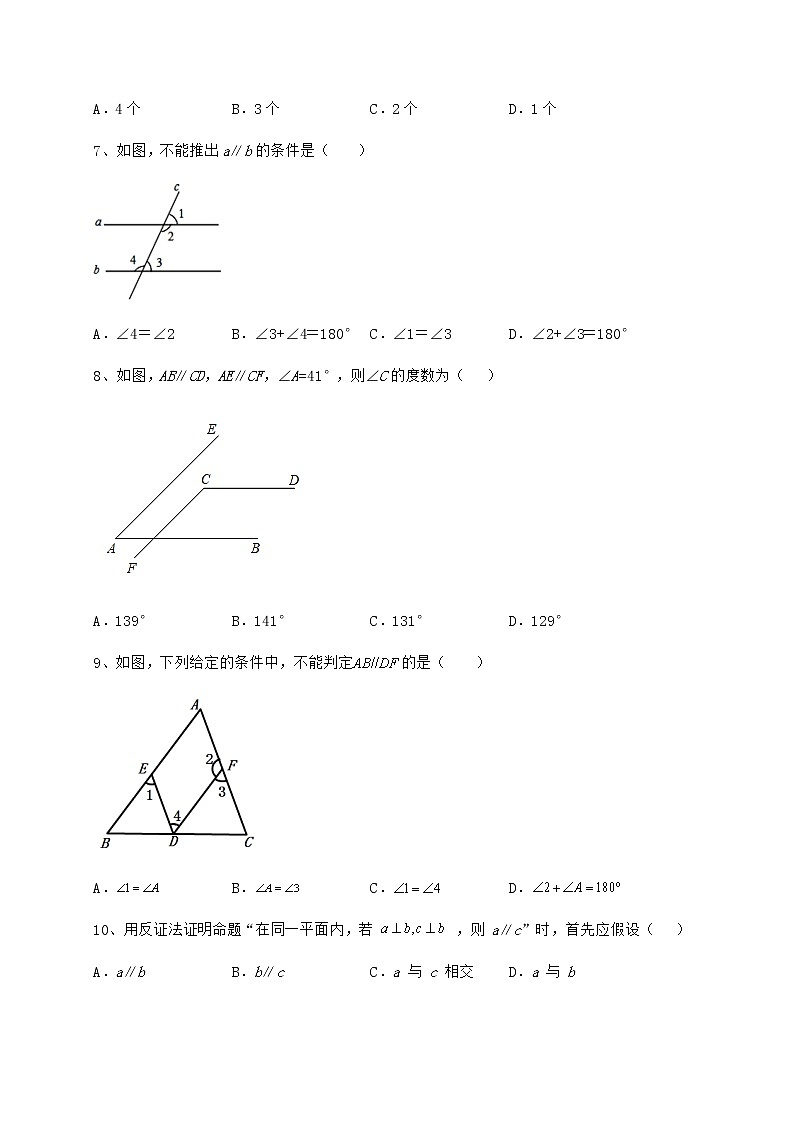
7、如图，不能推出a∥b的条件是（　　）

A．∠4＝∠2 B．∠3+∠4＝180° C．∠1＝∠3 D．∠2+∠3＝180°
8、如图，AB∥CD，AE∥CF，∠A=41°，则∠C的度数为（ ）

A．139° B．141° C．131° D．129°
9、如图，下列给定的条件中，不能判定的是（　　）

A． B． C． D．
10、用反证法证明命题“在同一平面内，若 ，则 a∥c”时，首先应假设（  ）
A．a∥b B．b∥c C．a 与 c 相交 D．a 与 b
第Ⅱ卷（非选择题 70分）
二、填空题（5小题，每小题4分，共计20分）
1、如图，已知ABCD，BE平分∠ABC，DE平分∠ADC，若∠ABC =m°，∠ADC =n°，则∠E=_________°．

2、如图，将一块直角三角板与一张两边平行的纸条按照如图所示的方式放置，下列结论：①∠1=∠2；②∠3=∠4；③∠2=∠3；④∠4+∠5=180°．其中正确的是________．（填序号）

3、如图，直线mn．若，，则的大小为_____度．

4、如图，已知，CE平分，，则______°．

5、如图，

（1）∠1和∠ABC是直线AB、CE被直线________所截得的________角；
（2）∠2和∠BAC是直线CE、AB被直线________所截得的________角；
（3）∠3和∠ABC是直线________、________被直线________所截得的________角；
（4）∠ABC和∠ACD是直线________、________被直线_________所截得的________角；
（5）∠ABC和∠BCE是直线________、________被直线________所截得的________角．
三、解答题（10小题，每小题5分，共计50分）
1、如图，运动会上，小明自踏板M处跳到沙坑P处，甲、乙、丙三名同学分别测得PM＝3.25米，PN＝3.15米，PF＝3.21米，则小明的成绩为 _____米．（填具体数值）

2、如图直线，直线与分别和交于点交直线b于点C．

（1）若，直接写出 ；
（2）若，则点B到直线的距离是 ；
（3）在图中直接画出并求出点A到直线的距离．
3、如图，，P为，之间的一点，已知，，求∠1的度数．

4、感知与填空：如图①，直线AB∥CD．求证：∠B+∠D=∠BED．
证明：过点E作直线EF∥CD，
∠2=______，（ ）
AB∥CD(已知），EF∥CD
_____∥EF，（ ）
∠B=∠1，（ ）
∠1+∠2=∠BED，
∠B+∠D=∠BED，（ ）
方法与实践：如图②，直线AB∥CD．若∠D=53°，∠B=22°，则∠E=______度．

5、已知AB∥CD，点E在AB上，点F在DC上，点G为射线EF上一点．
（基础问题）如图1，试说明：∠AGD＝∠A＋∠D．（完成图中的填空部分）．
证明：过点G作直线MN∥AB，
又∵AB∥CD，
∴MN∥CD（ 　 　）
∵MN∥AB，
∴∠A＝（ 　 　）（ 　 　）
∵MN∥CD，
∴∠D＝ 　 　（ 　 　）
∴∠AGD＝∠AGM＋∠DGM＝∠A＋∠D．
（类比探究）如图2，当点G在线段EF延长线上时，直接写出∠AGD、∠A、∠D三者之间的数量关系．
（应用拓展）如图3，AH平分∠GAB，DH交AH于点H，且∠GDH＝2∠HDC，∠HDC＝22°，∠H＝32°，直接写出∠DGA的度数．

6、如图，在ABC中，DEAC，DFAB．
（1）判断∠A与∠EDF之间的大小关系，并说明理由．
（2）求∠A+∠B+∠C的度数．

7、补全下列推理过程：已知：如图，CE平分∠BCD，∠1＝∠2＝70°，∠3＝40°，求证：AB∥CD．

证明：∵CE平分∠BCD（______）
∴∠1＝_____（_______）
∵∠1＝∠2＝70°（已知）
∴∠1＝∠2＝∠4＝70°（________）
∴AD∥BC（________）
∴∠D＝180°－_______＝180°－∠1－∠4＝40°
∵∠3＝40°（已知）
∴______＝∠3
∴AB∥CD（_______）
8、已知直线AB和CD交于点O，∠AOC＝α，∠BOE＝90°，OF平分∠AOD．

（1）当α＝30°时，则∠EOC＝_________°；∠FOD＝_________°．
（2）当α＝60°时，射线OE′从OE开始以12°/秒的速度绕点O逆时针转动，同时射线OF′从OF开始以8°/秒的速度绕点O顺时针转动，当射线OE′转动一周时射线OF′也停止转动，求经过多少秒射线OE′与射线OF′第一次重合？
（3）在（2）的条件下，射线OE′在转动一周的过程中，当∠E′OF′＝90°时，请直接写出射线OE′转动的时间为_________秒．
9、如图所示，点、分别在、上，、均与相交，，，求证：．

10、任意画两条相交的直线，在形成的四个角中，两两相配共能组成几对角？各对角存在怎样的位置关系？根据这种位置关系将它们分类．

-参考答案-
一、单选题
1、A
【分析】
过三角板的直角顶点作直尺两边的平行线，根据平行线的性质（两直线平行，同位角相等）即可求解．
【详解】
解：如图，过三角板的直角顶点作直尺两边的平行线，

∵直尺的两边互相平行，
∴，
∴，
∴，
故选：A．
【点睛】
本题考查平行线的性质，掌握平行线的性质是解题的关键．
2、D
【分析】
根据平行线的判定与性质、对顶角相等逐项判断即可．
【详解】
解：∵∠1=∠2，
∴AB∥CD，故A正确，不符合题意；
∴∠4=∠5，故C正确，不符合题意；
∵∠EFB与∠3是对顶角，
∴∠EFB=∠3，故B正确，
无法判断∠3=∠5，故D错误，符合题意，
故选：D．
【点睛】
本题考查平行线的判定与性质、对顶角相等，熟练掌握平行线的判定与性质是解答的关键．
3、B
【分析】
根据对顶角、同位角、内错角、同旁内角的特征去判断即可．
【详解】
∠1与∠2是同位角
故选：B
【点睛】
本题考查了同位角的含义，理解同位角的含义并正确判断同位角是关键．
4、A
【分析】
根据同位角相等、内错角相等、同旁内角互补的两直线平行分别判断即可．
【详解】
解：①∵，∴，无法推出；
②∵，∴；
③∵，∴，无法推出；
④∵，∴；
⑤∵∴，无法推出，
综上所述，能判断的是：②④，有2个，
故选：A．
【点睛】
题考查了平行线的判定，正确识别“三线八角”中的同位角、内错角、同旁内角是正确答题的关键，只有同位角相等、内错角相等、同旁内角互补，才能推出两被截直线平行．
5、A
【分析】
本题首先根据∠BGD′＝26°，可以得出∠AEG=∠BGD′＝26°,由折叠可知∠α=∠FED，由此即可求出∠α=77°．
【详解】
解：由图可知： AD∥BC
∴∠AEG=∠BGD′＝26°,
即：∠GED=154°，
由折叠可知: ∠α=∠FED，
∴∠α==77°
故选：A．
【点睛】
本题主要考察的是根据平行得性质进行角度的转化．
6、B
【分析】
根据同位角的定义判断即可；
【详解】
如图，与能构成同位角的有：∠1，∠2，∠3．

故选B．
【点睛】
本题主要考查了同位角的判断，准确分析判断是解题的关键．
7、B
【分析】
根据平行线的判定方法，逐项判断即可．
【详解】
解：、和是一对内错角，当时，可判断，故不符合题意；
、和是邻补角，当时，不能判定，故符合题意；
、和是一对同位角，当时，可判断，故不合题意；
、和是一对同旁内角，当时，可判断，故不合题意；
故选B．
【点睛】
本题考查了平行线的判定．解题的关键是：正确识别“三线八角”中的同位角、内错角、同旁内角是正确答题的关键．
8、A
【分析】
如图，根据AECF，得到∠CGB=41°，根据ABCD，即可得到∠C=139°．．
【详解】
解：如图，∵AECF，
∴∠A=∠CGB=41°，
∵ABCD，
∴∠C=180°-∠CGB=139°．

故选：A
【点睛】
本题考查了平行线的性质，熟知平行线的性质是解题关键．
9、A
【分析】
根据平行线的判定条件：同位角相等，两直线平行，同旁内角互补，两直线平行，内错角相等，两直线平行，进行逐一判断即可．
【详解】
解：A选项：当∠1=∠A时，可知是DE和AC被AB所截得到的同位角，可得到DE∥AC，而不是AB∥DF，故符合题意；
B选项：当∠A=∠3时，可知是AB、DF被AC所截得到的同位角，可得AB∥DF，故不符合题意；
C选项：当∠1=∠4时，可知是AB、DF被DE所截得到的内错角，可得AB∥DF，故不符合题意；
D选项：当∠2+∠A=180°时，是一对同旁内角，可得AB∥DF；故不符合题意；
故选A．
【点睛】
本题主要考查了平行线的判定，熟知平行线的判定条件是解题的关键．
10、C
【分析】
用反证法解题时，要假设结论不成立，即假设a与c不平行（或a与c相交）．
【详解】
解：原命题“在同一平面内，若a⊥b，c⊥b，则a∥c”，
用反证法时应假设结论不成立，
即假设a与c不平行（或a与c相交）．
故答案为：C．
【点睛】
此题考查了反证法证明的步骤：（1）假设原命题结论不成立；（2）根据假设进行推理，得出矛盾，说明假设不成立；（3）原命题正确．
二、填空题
1、
【分析】
作EF∥AB，证明AB∥ EF∥CD，进而得到∠BED=∠ABE+∠CDE，根据角平分线定义得到，即可求出．
【详解】
解：如图，作EF∥AB，
∵AB∥CD，
∴AB∥ EF∥CD，
∴∠ABE=∠BEF，∠CDE=∠DEF，
∴∠BED=∠BEF+∠DEF=∠ABE+∠CDE，
∵BE平分∠ABC，DE平分∠ADC，
∴，
∴ ．

故答案为：
【点睛】
本题考查了平行线性质，角平分线的定义，熟知角平分线的性质和平行公理的推论，根据题意添加辅助线是解题关键．
2、①②④
【分析】
根据平行线的性质，直角三角板的性质对各小题进行验证即可得解．
【详解】
解：∵纸条的两边互相平行，
∴∠1=∠2，∠3=∠4，∠4+∠5=180°，故①，②，④正确；
∵三角板是直角三角板，
∴∠2+∠4=180°-90°=90°，
∵∠3=∠4，
∴∠2+∠3=90°，故③不正确．
综上所述，正确的是①②④．
故答案为：①②④．
【点睛】
本题考查了平行线的性质，直角三角板的性质，熟记性质与概念并准确识图是解题的关键．
3、70
【分析】
如图（见解析），过点作，再根据平行线的性质可得，然后根据角的和差即可得．
【详解】
解：如图，过点作，
，
，
，
，
，
故答案为：70．

【点睛】
本题考查了平行线的性质与推论，熟练掌握平行线的性质是解题关键．
4、65
【分析】
由平行线的性质先求解再利用角平分线的定义可得答案.
【详解】
解： ， ，

CE平分，

故答案为：
【点睛】
本题考查的是角平分线的定义，平行线的性质，掌握“两直线平行，同旁内角互补”是解本题的关键.
5、BD（BC） 同位 AC 内错 AB AC BC 同旁内 AB AC BC 同位 AB CE BC 同旁内
【分析】
根据同位角、内错角、同旁内角的性质判断即可；
【详解】
（1）∠1和∠ABC是直线AB、CE被直线BD（BC）所截得的同位角；
（2）∠2和∠BAC是直线CE、AB被直线AC所截得的内错角；
（3）∠3和∠ABC是直线AB、AC被直线BC所截得的同旁内角；
（4）∠ABC和∠ACD是直线AB、AC被直线BC所截得的同位角；
（5）∠ABC和∠BCE是直线AB、CE被直线BC所截得的同旁内角．
故答案是：BD（BC）；同位；AC；内错；AB；AC；BC；同旁内；AB；AC；BC；同位；AB；CE；BC；同旁内．
【点睛】
本题主要考查了同位角、内错角、同旁内角的判断，准确分析判断是解题的关键．
三、解答题
1、3.15
【分析】
根据跳远的距离应该是起跳板到P点的垂线段的长度进行求解即可
【详解】
解：由图形可知，小明的跳远成绩应该为PN的长度，即3.15米，
故答案为：3.15．
【点睛】
本题主要考查了点到直线的距离，熟练掌握点到直线的距离的定义是解题的关键．
2、（1）；（2）4；（3）作图见详解；点A到直线BC的距离为．
【分析】
（1）根据平行线的性质：两直线平行，同旁内角互补及垂直的性质即可得；
（2）根据点到直线的距离可得点B到直线AC的距离为线段，由此即可得出结果；
（3）过点A作，点A到直线BC的距离为线段AD的长度，利用三角形等面积法即可得出．
【详解】
解：（1）∵，
∴，
∵，，
∴，
故答案为：；
（2）∵，
∴点B到直线AC的距离为线段，
故答案为：4；
（3）如图所示：过点A作，点A到直线BC的距离为线段AD的长度，

∵，
∴为直角三角形，
∴SΔABC=12×AC×AB=12×BC×AD，
即，
解得：，
∴点A到直线BC的距离为．
【点睛】
题目主要考查平行线的性质及点到直线的距离，熟练掌握等面积法求距离是解题关键．
3、30°
【分析】
首先过点P作射线，根据两直线平行，内错角相等，即可求得答案．
【详解】
过点P作射线，如图①．
∵，，
∴．
∴．
∵，∴．
又∵．
∴．

【点睛】
此题考查了平行线的判定与性质．平行线的判定是由角的数量关系判断两直线的位置关系，平行线的性质是由平行关系来寻找角的数量关系．
4、∠D；两直线平行，内错角相等；AB；两直线都和第三条直线平行，那么这两条直线也互相平行；两直线平行，内错角相等；等量代换；31．
【分析】
过点E作直线EF//CD，由两直线平行，内错角相等得出∠2=∠D；由两直线都和第三条直线平行，那么这两条直线也互相平行得出AB//EF；由两直线平行，内错角相等得出∠B=∠1；由∠1+∠2=∠BED，等量代换得出∠B+∠D=∠BED；方法与实践：如图②，由平行的性质可得∠BOD=∠D=53°，然后再根据三角形外角的性质解答即可
【详解】
解：过点E作直线EF∥CD，
∠2=∠D，（两直线平行，内错角相等）
AB∥CD(已知），EF∥CD
AB//EF，（两直线都和第三条直线平行，那么这两条直线也互相平行）
∠B=∠1，（两直线平行，内错角相等）
∠1+∠2=∠BED，
∠B+∠D=∠BED，（等量代换 ）
方法与实践：如图②，
∵直线AB∥CD
∴∠BOD=∠D=53°
∵∠BOD=∠E+∠B
∴∠E=∠BOD-∠B=53°- 22°=31°．
故答案依次为：∠D；两直线平行，内错角相等；AB；两直线都和第三条直线平行，那么这两条直线也互相平行；两直线平行，内错角相等；等量代换；31．

【点睛】
本题主要考查了平行线的判定与性质、三角形内角和定理等知识点；熟练掌握平行线的性质是解答本题的关键．
5、基础问题：平行于同一条直线的两条直线平行；∠AGM；两直线平行，内错角相等；∠DGM，两直线平行，内错角相等；类比探究：∠AGD＝∠A-∠D；应用拓展：42°．
【分析】
基础问题：由MN∥AB，可得∠A＝∠AGM，由MN∥CD，可得∠D＝∠DGM，则∠AGD＝∠AGM＋∠DGM＝∠A＋∠D；
类比探究：如图所示，过点G作直线MN∥AB，同理可得∠A＝∠AGM，∠D＝∠DGM，则∠AGD＝∠AGM-∠DGM＝∠A-∠D．
应用拓展：如图所示，过点G作直线MN∥AB，过点H作直线PQ∥AB，由MN∥AB，PQ∥AB，得到∠BAG＝∠AGM，∠BAH=∠AHP，由MN∥CD，PQ∥CD，得到∠CDG＝∠DGM，∠CDH=∠DHP，再由∠GDH＝2∠HDC，∠HDC＝22°，∠AHD＝32°，可得∠GDH=44°，∠DHP=22°，则∠CDG=66°，∠AHP=54°，∠DGM=66°，∠BAH=54°，再由AH平分∠BAG，即可得到∠AGM=108°，则∠AGD=∠AGM-∠DGM=42°．
【详解】
解：基础问题：过点G作直线MN∥AB，
又∵AB∥CD，
∴MN∥CD（平行于同一条直线的两条直线平行），
∵MN∥AB，
∴∠A＝∠AGM（两直线平行，内错角相等），
∵MN∥CD，
∴∠D＝∠DGM（两直线平行，内错角相等），
∴∠AGD＝∠AGM＋∠DGM＝∠A＋∠D．
故答案为：平行于同一条直线的两条直线平行；∠AGM；两直线平行，内错角相等；∠DGM，两直线平行，内错角相等；
类比探究：如图所示，过点G作直线MN∥AB，
又∵AB∥CD，
∴MN∥CD，
∵MN∥AB，
∴∠A＝∠AGM，
∵MN∥CD，
∴∠D＝∠DGM，
∴∠AGD＝∠AGM-∠DGM＝∠A-∠D．

应用拓展：如图所示，过点G作直线MN∥AB，过点H作直线PQ∥AB，
又∵AB∥CD，
∴MN∥CD，PQ∥CD
∵MN∥AB，PQ∥AB，
∴∠BAG＝∠AGM，∠BAH=∠AHP，
∵MN∥CD，PQ∥CD，
∴∠CDG＝∠DGM，∠CDH=∠DHP，
∵∠GDH＝2∠HDC，∠HDC＝22°，∠AHD＝32°，
∴∠GDH=44°，∠DHP=22°，
∴∠CDG=66°，∠AHP=54°，
∴∠DGM=66°，∠BAH=54°，
∵AH平分∠BAG，
∴∠BAG=2∠BAH=108°，
∴∠AGM=108°，
∴∠AGD=∠AGM-∠DGM=42°．

【点睛】
本题主要考查了平行线的性质，平行公理，解题的关键在于能够熟练掌握平行线的性质．
6、（1）两角相等，见解析；（2）180°
【分析】
（1）根据平行线的性质得到∠A=∠BED，∠EDF=∠BED，即可得到结论；
（2）根据平行线的性质得到∠C=∠EDB，∠B=∠FDC，利用平角的定义即可求解；
【详解】
（1）两角相等，理由如下：
∵DE∥AC，
∴∠A=∠BED(两直线平行，同位角相等).
∵DF∥AB，
∴∠EDF=∠BED(两直线平行，内错角相等)，
∴∠A=∠EDF(等量代换).
（2）∵DE∥AC，
∴∠C=∠EDB(两直线平行，同位角相等).
∵DF∥AB，
∴∠B=∠FDC(两直线平行，同位角相等).
∵∠EDB+∠EDF+∠FDC=180°，
∴∠A+∠B+∠C=180°(等量代换).
【点睛】
本题考查了平行线的性质，熟练掌握平行线的性质是解题的关键．
7、见解析
【分析】
由已知CE平分∠BCD可得∠1＝ ∠4，利用等式的性质得出∠1＝∠2＝∠4＝70°，根据直线判定定理得出AD∥BC，利用平角定义求出∠D＝180°－∠BCD即可．
【详解】
证明：∵CE平分∠BCD（ 已知 ），
∴∠1＝ ∠4 （ 角平分线定义 ），
∵∠1＝∠2＝70°已知，
∴∠1＝∠2＝∠4＝70°（等量代换），
∴AD∥BC（内错角相等，两直线平行），
∴∠D＝180°－∠BCD＝180°－∠1－∠4＝40°，
∵∠3＝40°已知，
∴ ∠D ＝∠3，
∴AB∥CD（内错角相等，两直线平行）．

故答案为：已知；∠4 ，角平分线定义 ；等量代换；内错角相等，两直线平行；∠BCD；∠D；内错角相等，两直线平行．
【点睛】
本题考查平行线判定，角平分线定义，平角，掌握平行线判定方法，角平分线定义，平角是解题关键．
8、（1）60，75；（2）秒；（3）3或12或21或30
【分析】
（1）根据题意利用互余和互补的定义可得：∠EOC与∠FOD的度数．
（2）由题意先根据，得出∠EOF=150°，则射线OE'、OF'第一次重合时，其OE'运动的度数+OF'运动的度数=150，列式解出即可；
（3）根据题意分两种情况在直线OE的左边和右边，进而根据其夹角列4个方程可得时间．
【详解】
解：（1）∵∠BOE=90°，
∴∠AOE=90°，
∵∠AOC=α＝30°，
∴∠EOC=90°-30°=60°，
∠AOD=180°-30°=150°，
∵OF平分∠AOD，
∴∠FOD=∠AOD=×150°=75°；
故答案为：60，75；
（2）当，．
设当射线与射线重合时至少需要t秒，
可得，解得：；
答：当射线与射线重合时至少需要秒；
（3）设射线转动的时间为t秒，
由题意得：或或或，
解得：或12或21或30．
答：射线转动的时间为3或12或21或30秒．
【点睛】
本题考查对顶角相等，邻补角互补的定义，角平分线的定义，角的计算，第三问有难度，熟记相关性质是解题的关键，注意要分情况讨论．
9、证明见解析
【分析】
由，证明，再证，最后根据对顶角相等，可得答案．
【详解】
证明：∵，
∴，
∴∠ABD=∠D，
又∵，
∴∠ABD=∠C，
∴，
∴，
∵，
∴．
【点睛】
本题主要考查了平行线的性质与判定，对顶角的性质，解题的关键在于能够熟练掌握相关知识进行求解．
10、共组成6对角，位置关系有两种：①有公共顶点，一边重合，另一边互为反向延长线；②有公共顶点，角的两边互为反向延长线，具体分类见解析
【分析】
根据题意画出图形，然后结合题意可进行求解．
【详解】
解：如图，

由图可知两条相交的直线，两两相配共组成6对角，
位置关系有两种：①有公共顶点，一边重合，另一边互为反向延长线；②有公共顶点，角的两边互为反向延长线，
这6对角中有：4对邻补角（即为∠AOD与∠AOC，∠AOD与∠BOD，∠BOD与∠BOC，∠BOC与∠AOC），
2对对顶角（即为∠AOD与∠BOC，∠BOD与∠AOC）．
【点睛】
本题主要考查对顶角及邻补角的概念，熟练掌握对顶角及邻补角的概念是解题的关键．