鲁教版 (五四制)六年级下册第七章 相交线与平行线综合与测试习题ppt课件

这是一份鲁教版 (五四制)六年级下册第七章 相交线与平行线综合与测试习题ppt课件，共18页。PPT课件主要包含了答案呈现，习题链接等内容，欢迎下载使用。

下面几种说法中，正确的是(　　)A．同一平面内不相交的两条线段平行B．同一平面内不相交的两条射线平行C．同一平面内不相交的两条直线平行D．以上三种说法都不正确
【点拨】根据平行线的定义判定两直线平行，一定要注意前提是“在同一平面内”，同时要注意在同一平面内，不相交的两条线段或两条射线不一定平行．
用一副三角尺拼图，并标点描线如图所示，然后过点C作CF平分∠DCE，交DE于点F.试说明：CF∥AB.
如图，在四边形ABCD中，∠ABC＝70°，∠C＝90°，∠ADC＝120°，DF平分∠ADC交BC于点F，点E在AD上，连接BE，且∠ABE：∠EBC＝4：3，试说明：BE∥DF.
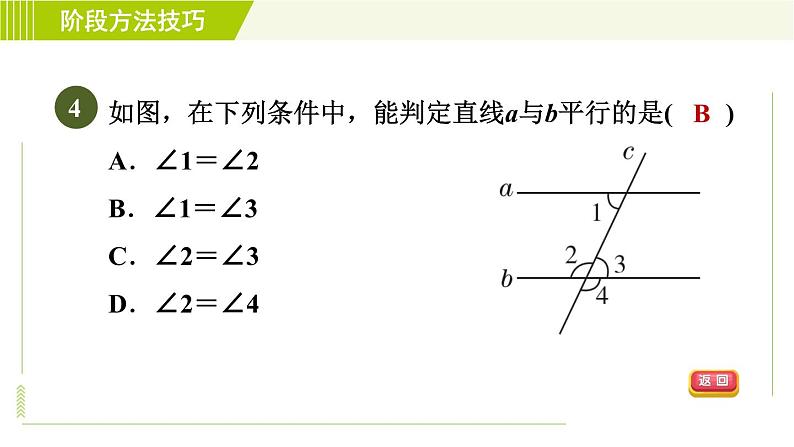
如图，在下列条件中，能判定直线a与b平行的是(　　)A．∠1＝∠2　 B．∠1＝∠3　C．∠2＝∠3　 D．∠2＝∠4
如图，要得到AD∥BC的结论，需要角相等的条件是__________________________(写出一个即可)．
∠EDC＝∠BCD(答案不唯一)
如图，已知∠ABC＝∠BCD，∠1＝∠2.试说明：BE∥CF.
解：因为∠ABC＝∠BCD，∠1＝∠2，所以∠ABC－∠1＝∠BCD－∠2，即∠EBC＝∠FCB.所以BE∥CF(内错角相等，两直线平行)．
如图，已知点E在BD上，AE⊥CE且EC平分∠DEF.(1)试说明：EA平分∠BEF；
解：因为AE⊥CE，所以∠AEC＝90°.所以∠2＋∠3＝90°且∠1＋∠4＝90°.又因为EC平分∠DEF，所以∠3＝∠4. 所以∠1＝∠2.所以EA平分∠BEF.
(2)若∠1＝∠A，∠4＝∠C，试说明：AB∥CD.
解：因为∠1＝∠A，∠4＝∠C，所以∠B＝180°－2∠1，∠D＝180°－2∠4.所以∠B＋∠D＝(180°－2∠1)＋(180°－2∠4)＝360°－2(∠1＋∠4)．又因为∠1＋∠4＝90°，所以∠B＋∠D＝360°－2×90°＝180°.所以AB∥CD.
如图，∠BEC＝95°，∠ABE＝120°，∠DCE＝35°，则AB与CD平行吗？请说明理由．
解：AB∥CD.理由：如图，延长BE交CD于点F，则直线CD，AB被直线BF所截．因为∠BEC＝95°，所以∠CEF＝180°－95°＝85°.因为∠DCE＝35°，
所以∠BFC＝180°－∠DCE－∠CEF＝180°－35°－85°＝60°.又因为∠ABE＝120°，所以∠ABE＋∠BFC＝180°.所以AB∥CD(同旁内角互补，两直线平行)．
【点拨】本题利用现有条件无法直接判断AB与CD是否平行，我们可考虑作一条辅助线，架起沟通AB与CD之间的桥梁．
解：AD∥EF.理由：因为∠2＝∠D，所以BC∥AD(同位角相等，两直线平行)．因为∠1＋∠B＝180°，所以EF∥BC(同旁内角互补，两直线平行)．所以AD∥EF(平行于同一条直线的两条直线平行)．
如图，∠1＋∠B＝180°，∠2＝∠D，则AD与EF平行吗？为什么？
【2020·金华】如图，工人师傅用角尺画出工件边缘AB的垂线a和b，得到a∥b.理由是(　　)A．连接直线外一点与直线上各点的所有线段中，垂线段最短B．在同一平面内，垂直于同一条直线的两条直线互相平行