2020-2021学年第2章 有理数2.11 有理数的乘方背景图ppt课件

这是一份2020-2021学年第2章 有理数2.11 有理数的乘方背景图ppt课件，共26页。PPT课件主要包含了我们把它记作，乘方的结果叫做幂，的10次方，-3的16次方，-a的17次方，的1次方，例1计算，跟踪训练，例2计算等内容，欢迎下载使用。

1.理解乘方的意义，能进行有理数的乘方运算.2.在观察、归纳、类比中养成分析问题、解决问题的能力.3.通过对大数的合理表示，认识、了解世界，在解决问题中获得成功的体验.
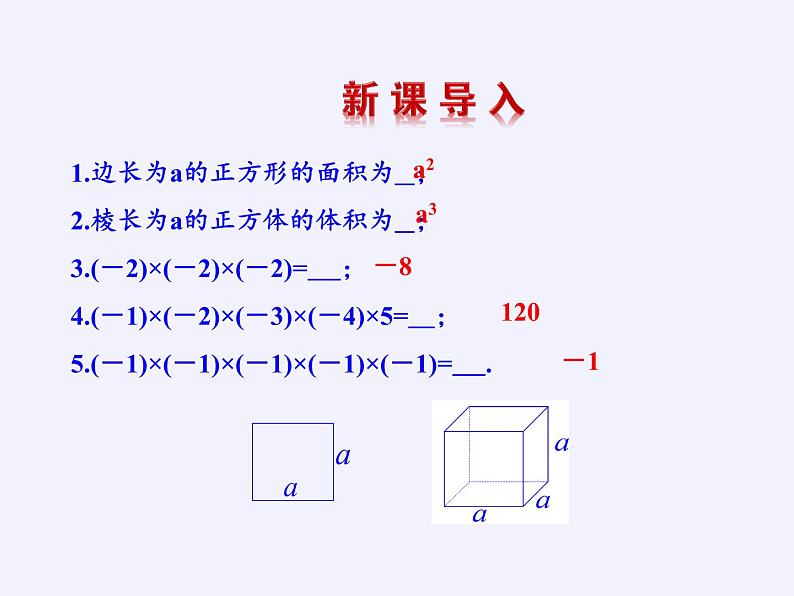
1.边长为a的正方形的面积为 ；2.棱长为a的正方体的体积为 ；3.(－2)×(－2)×(－2)= ；4.(－1)×(－2)×(－3)×(－4)×5= ；5.(－1)×(－1)×(－1)×(－1)×(－1)= .

将一张纸按下列要求对折: 对折2次可裁成4张，即2×2张；对折3次可裁成8张，即2×2×2张；若对折10次可裁成几张？请用一个算式表示（不用算出结果）若对折100次，算式中有几个2相乘？
对折10次裁成的张数用以下算式计算2×2×2×2×2×2×2×2×2×2是一个由10个2相乘的乘积式；
对折100次裁成的张数，可用算式 计算，在这个积中有100个2相乘.这么长的算式有简单的记法吗？
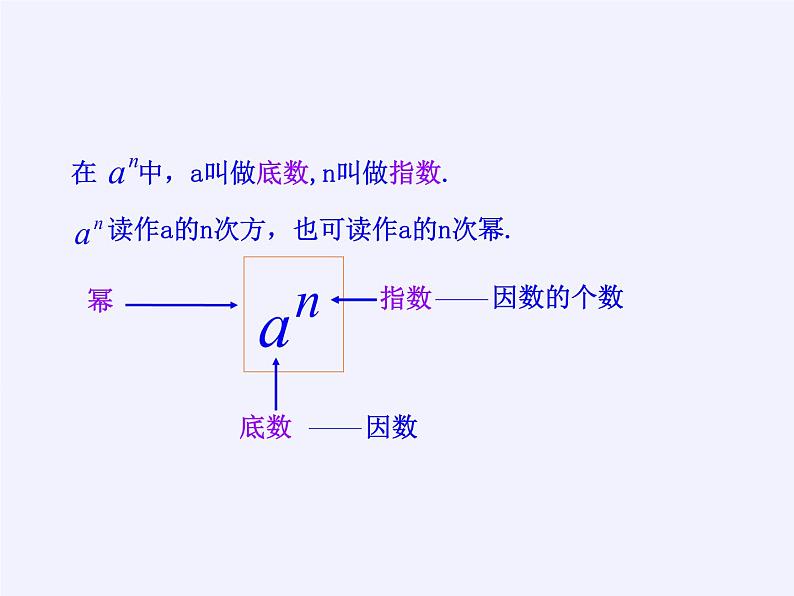
n个相同的因数a相乘，即
这种求几个相同因数的积的运算，叫做乘方.
（1）在1210中，12是 数，10是 数，读作 ；（2） 的底数是 ，指数是 ，读作 ；
（3）在 中，-3是 数，16是 数，读作 ； （4)在 中，底数是 ；指数是 ；读作 ；
（5）5看成幂的话，底数是 ，指数是 ，可读作 ； （6）a看成幂的话，底数是 ，指数是 ，可读作 .
1.把下列乘法式子写成乘方的形式：(1)1×1×1×1×1×1×1= ；(2)3×3×3×3×3= ；(3)（－3）×（－3）×（－3）×（－3）= ；(4) = .
二、把下列乘方写成乘法的形式：(1) = ；(2) = ；(3) = ；
思考：用乘方式子怎么表示 的相反数？
3.判断下列各式是否正确：（ ）(1)（ ）(2)（ ）(3）（ ）(4）
例1的两个幂，底数都是负数，为什么这两个幂一个是负数而另一个是正数呢？是由什么数来确定它们的正负呢？
当底数是负数时，幂的正负由指数确定，指数是偶数时，幂是正数；指数是奇数时，幂是负数.
如果幂的底数是正数，那么这个幂有可能是负数吗？
不可能！正数的任何次幂都是正数.
1.口答（1） 是 （填“正”或“负”）数；（2） 是 （填“正”或“负”）数；（3） = ；（4） = .
2.计算：(1) = ； (2) = ；(3) = ； (4) = ；(5) = ； (6) = ；(7) = ； (8) = .
先算乘方，再算乘除，最后算加减
1.填空（1）在46中，底数是 ，指数是 ，（2） 读作 ；（3） 的结果是 数（填“正”或“负”）（4）计算： = ；（5）计算： = ；（6）计算: .
-4的7次方或-4的7次幂
2.计算-1-2×（-3）2的结果等于（ ）A.-19 B.19 C.7 D.-7【解析】选A.-1-2×（-3）2=(-1)+(-18)=-19.
3.计算127(32)16(4)2的值为（ ）A． 36 B．164 C．216 D．237 【解析】选D.127(32)16(4)2=12+224+1=236+1=237
4.（江西·中考）按照下图所示的操作步骤，若输入x的值为－2，则给出的值为 ．【解析】如图所示的式子为(-2)2×3-5=4×3-5 =12-5=7.答案: 7
1.乘方是特殊的乘法运算，所谓特殊就是所乘的因数是相同的；2.幂是乘方的结果；正数的任何次幂都是正数，负数的奇次幂是负数，负数的偶次幂是正数；3.进行乘方运算应先定符号后计算.
人的生命当如流水一般，自己快乐着又润泽一方.