2020-2021学年14.1 全等三角形复习课件ppt

这是一份2020-2021学年14.1 全等三角形复习课件ppt，共17页。PPT课件主要包含了定义重合法，SSS，SAS，ASA，AAS，包括直角三角形，知识小结等内容，欢迎下载使用。

一般三角形 全等的条件：
直角三角形 全等特有的条件：
不包括其它形状的三角形
三角形全等的证题思路：
1.证明两个三角形全等，要结合题目的条件和结论，选择恰当的判定方法2.全等三角形，是证明两条线段或两个角相等的重要方法之一，证明时 　①要观察待证的线段或角，在哪两个可能全等的三角形中。 　②分析要证两个三角形全等，已有什么条件，还缺什么条件。 　③有公共边的，公共边一定是对应边， 有公共角的，公共角一定是对应角，有对顶角，对顶角也是对应角总之，证明过程中能用简单方法的就不要绕弯路。
例1：如图，D在AB上，E在AC上，且∠B =∠C，那么补充下列一具条件后，仍无法判定△ABE≌△ACD的是( )A．AD=AEB． ∠AEB=∠ADCC．BE=CD D．AB=AC
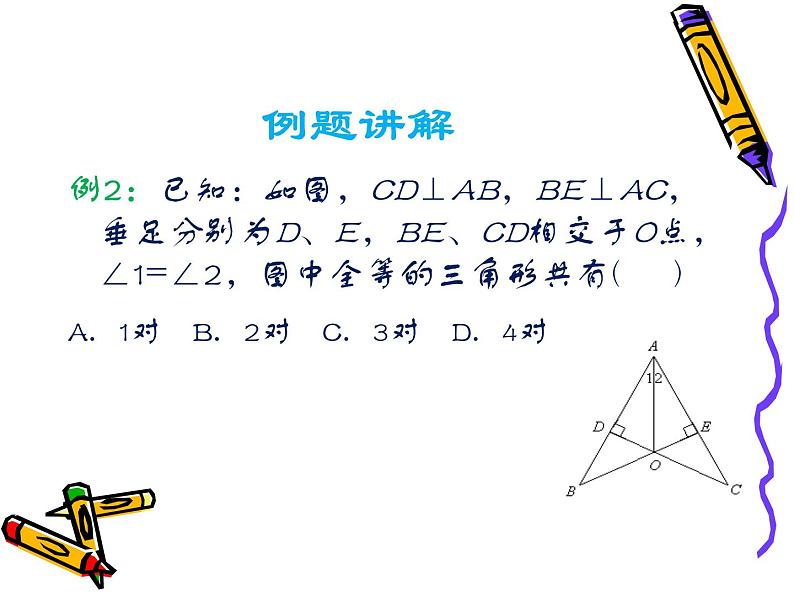
例2：已知：如图，CD⊥AB，BE⊥AC，垂足分别为D、E，BE、CD相交于O点，∠1=∠2，图中全等的三角形共有( )A．1对 B．2对 C．3对 D．4对
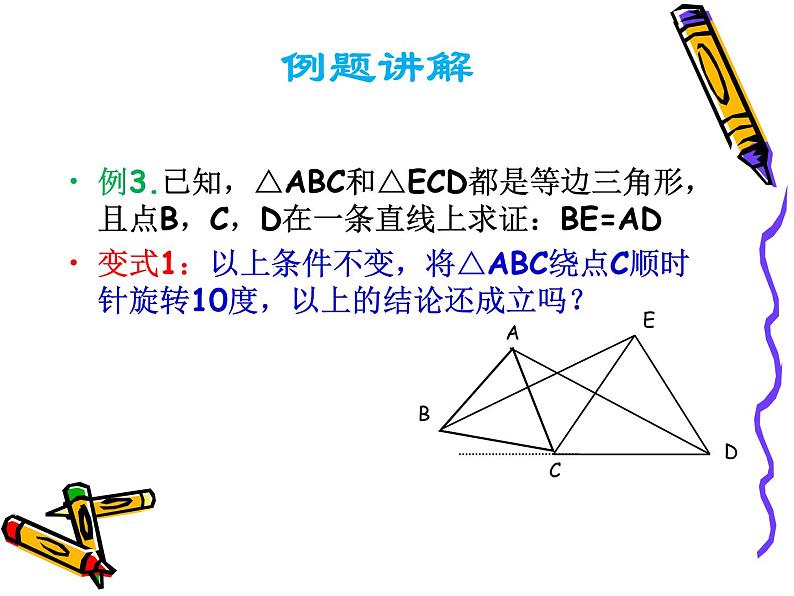
例3.已知，△ABC和△ECD都是等边三角形，且点B，C，D在一条直线上求证：BE=AD变式1：以上条件不变，将△ABC绕点C顺时针旋转10度，以上的结论还成立吗？
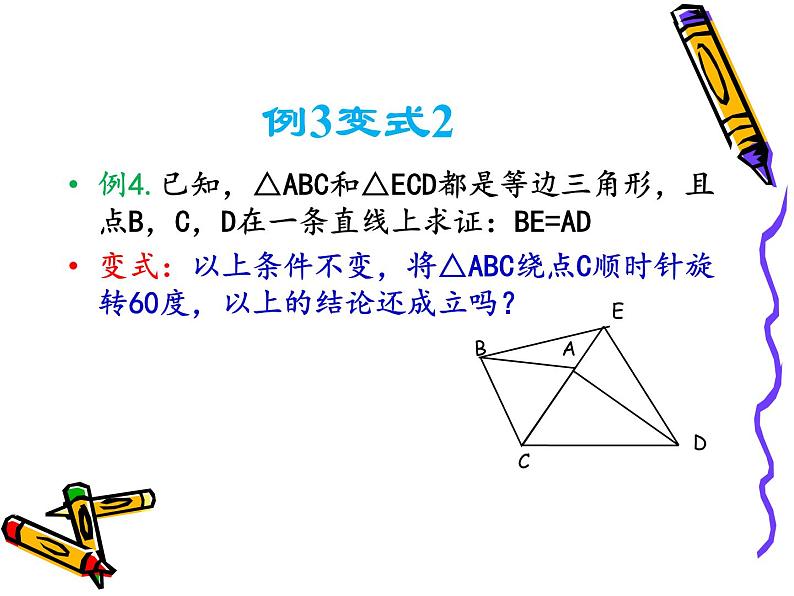
例4.已知，△ABC和△ECD都是等边三角形，且点B，C，D在一条直线上求证：BE=AD变式：以上条件不变，将△ABC绕点C顺时针旋转60度，以上的结论还成立吗？
例5.已知，△ABC和△ECD都是等边三角形，当△ABC绕点C顺时针旋转ɑ时，连接BE，DA；结论BE=AD还成立吗？若成立请加以证明。
例3变式4引申：例6.已知，△ABC和△ECD都是等边三角形，且点B，C，D在一条直线上，AC与BE相交于M，CE与AD相交于N，试判定△ＣＭＮ的形状
解：△ＣＭＮ是等边三角形
（１）先证∠ACE＝６０°
（２）证明△BCE≌△ACD→∠BEC＝∠ADC
（３）在证△MCE≌△NCD→CM=CN
1.已知BD＝CD，∠ABD＝∠ACD，DE、DF分别垂直于AB及AC交延长线于E、F，求证：DE＝DF
2.点A、F、E、C在同一直线上，AF＝CE，BE = DF，BE∥DF，求证：AB∥CD。
3.已知点A，E，F，C在同一条直线上，且AE＝CF，过E　F两点分别作DE⊥AC，BF⊥AC，且AB＝CD，（１）求证：BD平分 EF（2）若将△DEC的边EC沿AC方向移动，变化为2时，其余条件不变，上述结论是否成立，说明理由
4.如图在三角形ABC中，BC上的高为AD，且∠B=2∠C求证：CD=AB＋BD
5.如图：在四边形ABCD中，点E在边CD上，连接AE、BE并延长AE交BC的延长线于点F，给出下列5个关系式：：①AD∥BC，②，DE=EC③∠1=∠2，④∠3=∠4，⑤AD+BC=AB。将其中三个关系式作为已知，另外两个作为结论，构成正确的命题。请用序号写出两个正确的命题：（书写形式：如果……那么……）（1） ；（2） ；
1、全等三角形的概念——2、全等三角形的性质——3、全等三角形的判定方法
对应边相等、对应角相等