初中数学沪科版九年级下册第24章 圆综合与测试达标测试

这是一份初中数学沪科版九年级下册第24章 圆综合与测试达标测试，共34页。试卷主要包含了下列说法正确的个数有等内容，欢迎下载使用。
沪科版九年级数学下册第24章圆综合测评
考试时间：90分钟；命题人：数学教研组
考生注意：
1、本卷分第I卷（选择题）和第Ⅱ卷（非选择题）两部分，满分100分，考试时间90分钟
2、答卷前，考生务必用0.5毫米黑色签字笔将自己的姓名、班级填写在试卷规定位置上
3、答案必须写在试卷各个题目指定区域内相应的位置，如需改动，先划掉原来的答案，然后再写上新的答案；不准使用涂改液、胶带纸、修正带，不按以上要求作答的答案无效。
第I卷（选择题 30分）
一、单选题（10小题，每小题3分，共计30分）
1、如图，在△ABC中，∠BAC＝130°，将△ABC绕点C逆时针旋转得到△DEC，点A，B的对应点分别为D，E，连接AD．当点A，D，E在同一条直线上时，则∠BAD的大小是（　　）

A．80° B．70° C．60° D．50°
2、在下列图形中，既是中心对称图形又是轴对称图形的是（ ）
A． B．
C． D．
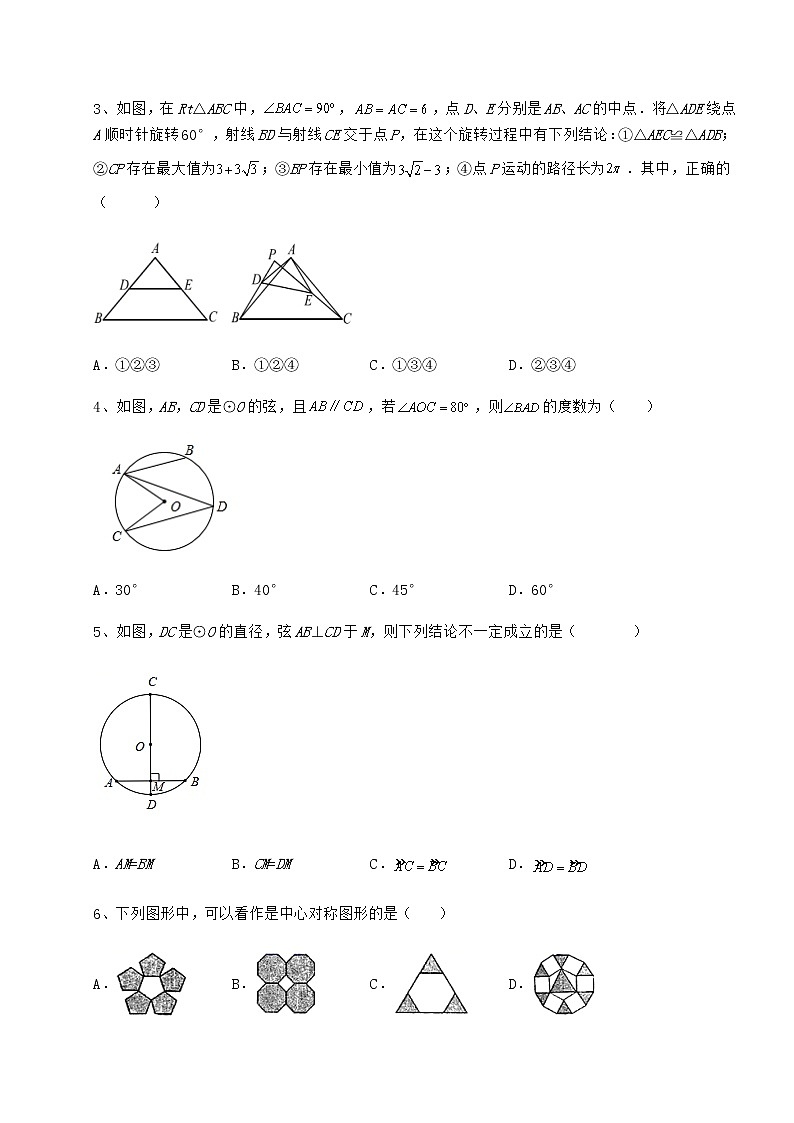
3、如图，在Rt△ABC中，，，点D、E分别是AB、AC的中点．将△ADE绕点A顺时针旋转60°，射线BD与射线CE交于点P，在这个旋转过程中有下列结论：①△AEC≌△ADB；②CP存在最大值为；③BP存在最小值为；④点P运动的路径长为．其中，正确的（ ）

A．①②③ B．①②④ C．①③④ D．②③④
4、如图，AB，CD是⊙O的弦，且，若，则的度数为（ ）

A．30° B．40° C．45° D．60°
5、如图，DC是⊙O的直径，弦AB⊥CD于M，则下列结论不一定成立的是（　　　　）

A．AM=BM B．CM=DM C． D．
6、下列图形中，可以看作是中心对称图形的是（ ）
A． B． C． D．
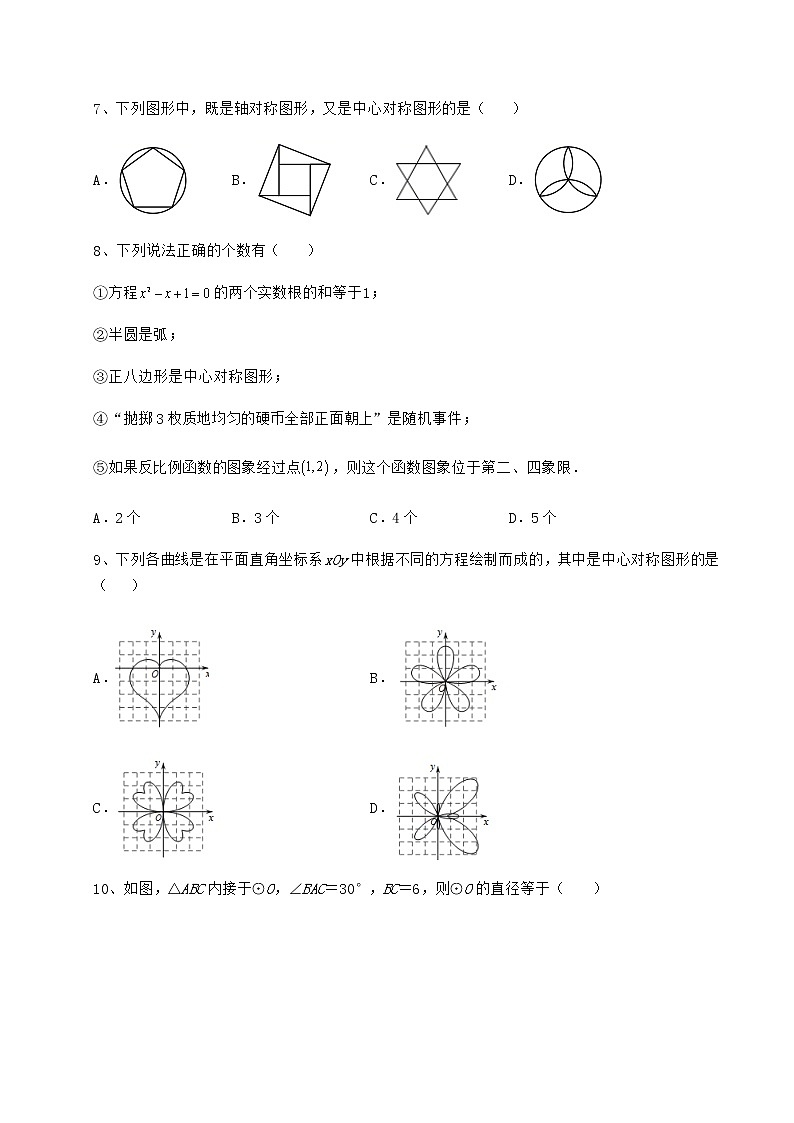
7、下列图形中，既是轴对称图形，又是中心对称图形的是（　　）
A． B． C． D．
8、下列说法正确的个数有（ ）
①方程的两个实数根的和等于1；
②半圆是弧；
③正八边形是中心对称图形；
④“抛掷3枚质地均匀的硬币全部正面朝上”是随机事件；
⑤如果反比例函数的图象经过点，则这个函数图象位于第二、四象限．
A．2个 B．3个 C．4个 D．5个
9、下列各曲线是在平面直角坐标系xOy中根据不同的方程绘制而成的，其中是中心对称图形的是（ ）
A． B．
C． D．
10、如图，△ABC内接于⊙O，∠BAC＝30°，BC＝6，则⊙O的直径等于（　　）

A．10 B．6 C．6 D．12
第Ⅱ卷（非选择题 70分）
二、填空题（5小题，每小题4分，共计20分）
1、如图，正方形ABCD的边长为1，⊙O经过点C，CM为⊙O的直径，且CM＝1．过点M作⊙O的切线分别交边AB，AD于点G，H．BD与CG，CH分别交于点E，F，⊙O绕点C在平面内旋转（始终保持圆心O在正方形ABCD内部）．给出下列四个结论：
①HD＝2BG；②∠GCH＝45°；③H，F，E，G四点在同一个圆上；④四边形CGAH面积的最大值为2．其中正确的结论有 _____（填写所有正确结论的序号）．

2、如图，将半径为的圆形纸片沿一条弦折叠，折叠后弧的中点与圆心重叠，则弦的长度为________．

3、如图，已知扇形的圆心角为60°，半径为2，则图中弓形（阴影部分）的面积为______．

4、如图，将矩形绕点A顺时针旋转到矩形的位置，旋转角为．若，则的大小为________（度）．

5、如图，PM，PN分别与⊙O相切于A，B两点，C为⊙O上异于A，B的一点，连接AC，BC．若∠P＝58°，则∠ACB的大小是___________．

三、解答题（5小题，每小题10分，共计50分）
1、定理：一条弧所对的圆周角等于这条弧所对的圆心角的一半．如图1，∠A＝∠O．
已知：如图2，AC是⊙O的一条弦，点D在⊙O上（与A、C不重合），联结DE交射线AO于点E，联结OD，⊙O的半径为5，tan∠OAC＝．

（1）求弦AC的长．
（2）当点E在线段OA上时，若△DOE与△AEC相似，求∠DCA的正切值．
（3）当OE＝1时，求点A与点D之间的距离（直接写出答案）．
2、如图，在方格纸中，已知顶点在格点处的△ABC，请画出将△ABC绕点C旋转180°得到的△A'B'C'．（需写出△A'B'C'各顶点的坐标）．

3、正方形绿化场地拟种植两种不同颜色（用阴影部分和非阴影部分表示）的花卉，要求种植的花卉能组成轴对称或中心对称图案，下面是三种不同设计方案中的一部分．

（1）请把图①、图②补成既是轴对称图形，又是中心对称图形，并画出一条对称轴；
（2）把图③补成只是中心对称图形，并把中心标上字母P．
4、问题：如图，是的直径，点在内，请仅用无刻度的直尺，作出中边上的高.
小芸解决这个问题时，结合圆以及三角形高线的相关知识，设计了如下作图过程．
作法：如图，
①延长交于点，延长交于点；
②分别连接，并延长相交于点；
③连接并延长交于点．

所以线段即为中边上的高．
（1）根据小芸的作法，补全图形；
（2）完成下面的证明．
证明：∵是的直径，点，在上，
∴________°．（______）（填推理的依据）
∴，．
∴，________是的两条高线．
∵，所在直线交于点，
∴直线也是的高所在直线．
∴是中边上的高．
5、如图①，在Rt△ABC中，∠BAC = 90°，AB = k·AC，△ADE是由△ABC绕点A逆时针旋转某个角度得到的，BC与DE交于点F，直线BD与EC交于点G
（1）求证：BD = k·EC；
（2）求∠CGD的度数；
（3）若k = 1（如图②），求证：A，F，G三点在同一直线上．


-参考答案-
一、单选题
1、A
【分析】
根据三角形旋转得出，，根据点A，D，E在同一条直线上利用邻补角关系求出，根据等腰三角形的性质即可得到∠DAC=50°，由此即可求解．
【详解】
证明：∵绕点C逆时针旋转得到，
∴，，
∴∠ADC=∠DAC，
∵点A，D，E在同一条直线上，
∴，
∴∠DAC=50°，
∴∠BAD=∠BAC-∠DAC=80°
故选A．
【点睛】
本题考查三角形旋转性质，邻补角的性质，等腰三角形的性质与判定，解题的关键在于熟练掌握旋转的性质．
2、B
【分析】
根据中心对称图形与轴对称图形的定义解答即可.
【详解】
解：A.是轴对称图形，不是中心对称图形，不符合题意；
B既是中心对称图形又是轴对称图形，符合题意；
C. 是轴对称图形，不是中心对称图形，不符合题意；
D. 既不是中心对称图形，也不是轴对称图形，不符合题意.
故选B.
【点睛】
本题主要考查的是中心对称图形与轴对称图形的定义.一个图形沿一条直线折叠，直线两旁的部分能够完全重合的图形叫作轴对称图形；把一个图形绕着某个点旋转180°，如果旋转后的图形与另一个图形重合叫作中心对称图形.
3、B
【分析】
根据，，点D、E分别是AB、AC的中点．得出∠DAE=90°，AD=AE=，可证∠DAB=∠EAC，再证△DAB≌△EAC（SAS），可判断①△AEC≌△ADB正确；作以点A为圆心，AE为半径的圆，当CP为⊙A的切线时，CP最大，根据△AEC≌△ADB，得出∠DBA=∠ECA，可证∠P=∠BAC=90°，CP为⊙A的切线，证明四边形DAEP为正方形，得出PE=AE=3，在Rt△AEC中，CE=，可判断②CP存在最大值为正确；△AEC≌△ADB，得出BD=CE=，在Rt△BPC中，BP最小=可判断③BP存在最小值为不正确；取BC中点为O，连结AO，OP，AB=AC=6，∠BAC=90°，BP=CO=AO=，当AE⊥CP时,CP与以点A为圆心，AE为半径的圆相切，此时sin∠ACE=，可求∠ACE=30°，根据圆周角定理得出∠AOP=2∠ACE=60°，当AD⊥BP′时，BP′与以点A为圆心，AE为半径的圆相切，此时sin∠ABD=，可得∠ABD=30°根据圆周角定理得出∠AOP′=2∠ABD=60°，点P在以点O为圆心，OA长为半径，的圆上运动轨迹为，L可判断④点P运动的路径长为正确即可．
【详解】
解：∵，，点D、E分别是AB、AC的中点．
∴∠DAE=90°，AD=AE=，
∴∠DAB+∠BAE=90°，∠BAE+∠EAC=90°，
∴∠DAB=∠EAC，
在△DAB和△EAC中，
，
∴△DAB≌△EAC（SAS），
故①△AEC≌△ADB正确；

作以点A为圆心，AE为半径的圆，当CP为⊙A的切线时，CP最大，
∵△AEC≌△ADB，
∴∠DBA=∠ECA，
∴∠PBA+∠P=∠ECP+∠BAC，
∴∠P=∠BAC=90°，
∵CP为⊙A的切线，
∴AE⊥CP，
∴∠DPE=∠PEA=∠DAE=90°，
∴四边形DAEP为矩形，
∵AD=AE，
∴四边形DAEP为正方形，
∴PE=AE=3，
在Rt△AEC中，CE=，
∴CP最大=PE+EC=3+，
故②CP存在最大值为正确；

∵△AEC≌△ADB，
∴BD=CE=，
在Rt△BPC中，BP最小=，
BP最短=BD-PD=-3，
故③BP存在最小值为不正确；
取BC中点为O，连结AO，OP，
∵AB=AC=6，∠BAC=90°，
∴BP=CO=AO=，
当AE⊥CP时,CP与以点A为圆心，AE为半径的圆相切，此时sin∠ACE=，
∴∠ACE=30°，
∴∠AOP=2∠ACE=60°，
当AD⊥BP′时，BP′与以点A为圆心，AE为半径的圆相切，此时sin∠ABD=，
∴∠ABD=30°，
∴∠AOP′=2∠ABD=60°，
∴点P在以点O为圆心，OA长为半径，的圆上运动轨迹为，
∵∠POP=∠POA+∠AOP′=60°+60°=120°，
∴L．
故④点P运动的路径长为正确；
正确的是①②④．
故选B．

【点睛】
本题考查图形旋转性质，线段中点定义，三角形全等判定与性质，圆的切线，正方形判定与性质，勾股定理，锐角三角函数，弧长公式，本题难度大，利用辅助线最长准确图形是解题关键．
4、B
【分析】
由同弧所对的圆周角是圆心角的一半可得，利用平行线的性质：两直线平行，内错角相等即可得．
【详解】
解：∵，
∴，
∵，
∴，
故选：B．
【点睛】
题目主要考查圆周角定理，平行线的性质等，理解题意，找出相关的角度是解题关键．
5、B
【分析】
根据垂径定理“垂直于弦的直径平分这条弦，并且平分弦所对的两条弧”进行判断即可得．
【详解】
解：∵弦AB⊥CD，CD过圆心O，
∴AM=BM，，，
即选项A、C、D选项说法正确，不符合题意，
当根据已知条件得CM和DM不一定相等，
故选B．
【点睛】
本题考查了垂径定理，解题的关键是掌握垂径定理．
6、B
【分析】
把一个图形绕某一点旋转180°，如果旋转后的图形能够与原来的图形重合，那么这个图形就叫做中心对称图形，根据中心对称图形的概念求解．
【详解】
A．不是中心对称图形，故本选项不符合题意；
B．是中心对称图形，故本选项符合题意；
C．不是中心对称图形，故本选项不符合题意；
D．不是中心对称图形，故本选项不符合题意．
故选：B．
【点睛】
本题考查了中心对称图形的概念，中心对称图形是要寻找对称中心，旋转180度后与原图重合．
7、C
【详解】
解：选项A是轴对称图形，不是中心对称图形，故A不符合题意；
选项B不是轴对称图形，是中心对称图形，故B不符合题意；
选项C既是轴对称图形，也是中心对称图形，故C符合题意；
选项D是轴对称图形，不是中心对称图形，故D不符合题意；
故选C
【点睛】
本题考查的是轴对称图形的识别，中心对称图形的识别，掌握“轴对称图形与中心对称图形的定义”是解本题的关键，轴对称图形：把一个图形沿某条直线对折，直线两旁的部分能够完全重合；中心对称图形：把一个图形绕某点旋转后能与自身重合.
8、B
【分析】
根据所学知识对五个命题进行判断即可．
【详解】
1、Δ=12-4×1=-3