初中数学沪科版九年级下册第24章 圆综合与测试一课一练

这是一份初中数学沪科版九年级下册第24章 圆综合与测试一课一练，共27页。试卷主要包含了下列图形中，是中心对称图形的是，下列语句判断正确的是等内容，欢迎下载使用。
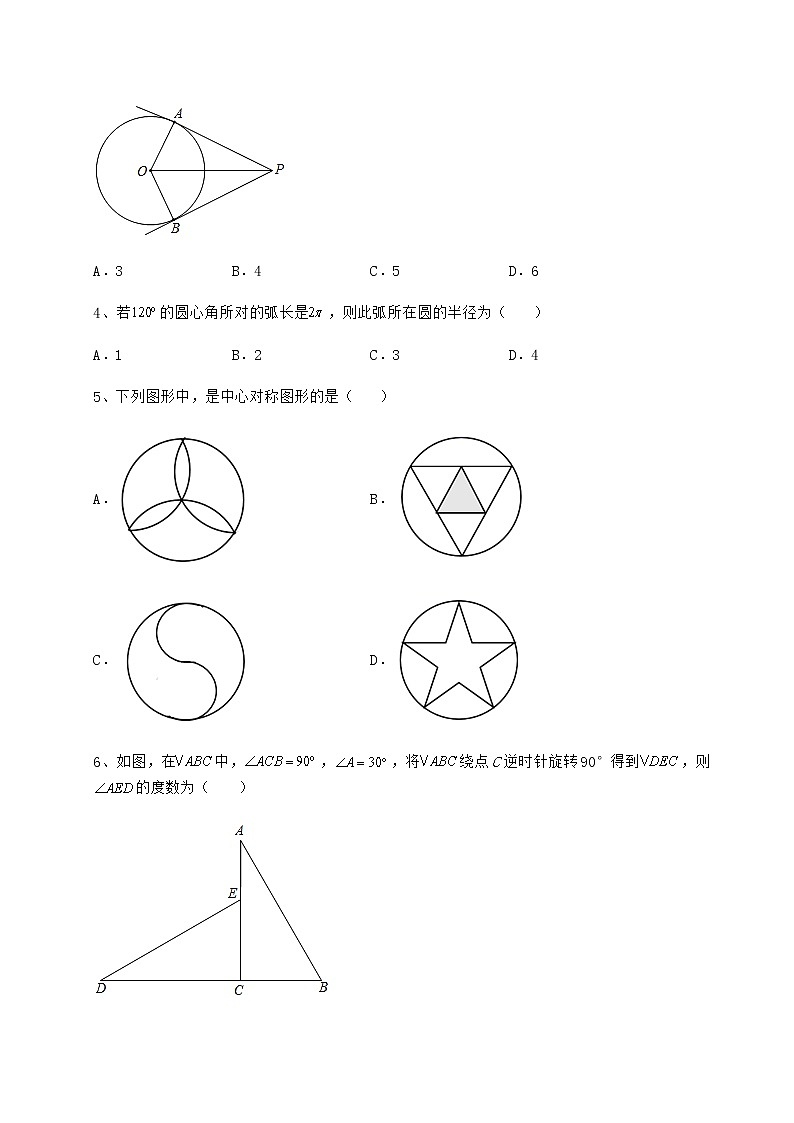
沪科版九年级数学下册第24章圆定向测评 考试时间：90分钟；命题人：数学教研组考生注意：1、本卷分第I卷（选择题）和第Ⅱ卷（非选择题）两部分，满分100分，考试时间90分钟2、答卷前，考生务必用0.5毫米黑色签字笔将自己的姓名、班级填写在试卷规定位置上3、答案必须写在试卷各个题目指定区域内相应的位置，如需改动，先划掉原来的答案，然后再写上新的答案；不准使用涂改液、胶带纸、修正带，不按以上要求作答的答案无效。第I卷（选择题  30分）一、单选题（10小题，每小题3分，共计30分）1、如图，是△ABC的外接圆，已知，则的大小为（      ）A．55° B．60° C．65° D．75°2、如图，AB是的直径，的弦DC的延长线与AB的延长线相交于点P，于点E，，，则阴影部分的面积为（    ）A． B． C． D．3、如图，PA，PB是⊙O的切线，A，B为切点，PA＝4，则PB的长度为（    ）A．3 B．4 C．5 D．64、若的圆心角所对的弧长是，则此弧所在圆的半径为（    ）A．1 B．2 C．3 D．45、下列图形中，是中心对称图形的是（    ）A． B．C． D．6、如图，在中，，，将绕点C逆时针旋转90°得到，则的度数为（    ）A．105° B．120° C．135° D．150°7、如图，与的两边分别相切，其中OA边与相切于点P．若，，则OC的长为（    ）A．8 B． C． D．8、如图，圆形螺帽的内接正六边形的面积为24cm2，则圆形螺帽的半径是（　　）A．1cm B．2cm C．2cm D．4cm9、下列语句判断正确的是（　　）A．等边三角形是轴对称图形，但不是中心对称图形B．等边三角形既是轴对称图形，又是中心对称图形C．等边三角形是中心对称图形，但不是轴对称图形D．等边三角形既不是轴对称图形，也不是中心对称图形10、如图，在△ABC中，∠CAB=64°，将△ABC在平面内绕点A旋转到△AB′C′的位置，使CC′AB，则旋转角的度数为（    ）A．64° B．52° C．42° D．36°第Ⅱ卷（非选择题  70分）二、填空题（5小题，每小题4分，共计20分）1、如图，将矩形绕点A顺时针旋转到矩形的位置，旋转角为．若，则的大小为________（度）．2、如图，AB为⊙O的弦，∠AOB=90°，AB=a，则OA=______，O点到AB的距离=______．3、如图，在⊙O中，∠BOC=80°，则∠A=___________°．4、圆锥的母线长为，底面圆半径为r，则全面积为______．5、如图，在⊙O中，＝，AB＝10，BC＝12，D是上一点，CD＝5，则AD的长为______．三、解答题（5小题，每小题10分，共计50分）1、问题：如图，是的直径，点在内，请仅用无刻度的直尺，作出中边上的高.小芸解决这个问题时，结合圆以及三角形高线的相关知识，设计了如下作图过程．作法：如图，①延长交于点，延长交于点；②分别连接，并延长相交于点；③连接并延长交于点．所以线段即为中边上的高．（1）根据小芸的作法，补全图形；（2）完成下面的证明．证明：∵是的直径，点，在上，∴________°．（______）（填推理的依据）∴，．∴，________是的两条高线．∵，所在直线交于点，∴直线也是的高所在直线．∴是中边上的高．2、如图，A，P，B，C是⊙O上的四点，∠APC＝∠CPB＝60°．（1）判断△ABC的形状，并证明你的结论；（2）求证：PA＋PB＝PC．3、如图，在等边中，D为BC边上一点，连接AD，将沿AD翻折得到，连接BE并延长交AD的延长线于点F，连接CF．（1）若，求的度数；（2）若，求的大小；（3）猜想CF，BF，AF之间的数量关系，并证明．4、新定义：如图①，已知，在内部画射线OC，得到三个角，分别为、、．若这三个角中有一个角是另外一个角的2倍，则称射线OC为的“幸运线”．（本题中所研究的角都是大于0°而小于180°的角．）（阅读理解）（1）角的平分线______这个角的“幸运线”；（填“是”或“不是”）（初步应用）（2）如图①，，射线OC为的“幸运线”，则的度数为______；（直接写出答案）（解决问题）（3）如图②，已知，射线OM从OA出发，以每秒10°的速度绕O点顺时针旋转，同时，射线ON从OB出发，以每秒15°的速度绕O点顺时针旋转，设运动的时间为t秒．若OM、ON、OB三条射线中，一条射线恰好是以另外两条射线为边的角的“幸运线”，求运动的时间t的值．（实际运用）（4）周末，小丽帮妈妈到附近的“中通快递”网点取包裹，出家门时小丽看了看时钟，恰好是下午3点整，取好包裹回到家时，小丽再看了看时钟，还没有到下午3点半，但此时分针与时针恰好重合．问小丽帮妈妈取包裹用了多少分钟？5、如图，AB是⊙O的直径，点D，E在⊙O上，四边形BDEO是平行四边形，过点D作交AE的延长线于点C．（1）求证：CD是⊙O的切线．（2）若，求阴影部分的面积． -参考答案-一、单选题1、C【分析】由OA=OB，，求出∠AOB=130°，根据圆周角定理求出的度数．【详解】解：∵OA=OB，，∴∠BAO=．∴∠AOB=130°．∴=∠AOB=65°．故选：C．【点睛】此题考查了同圆中半径相等的性质，圆周角定理：同弧所对的圆周角等于圆心角的一半．2、B【分析】由垂径定理可知，AE=CE，则阴影部分的面积等于扇形AOD的面积，求出，然后利用扇形面积公式，即可求出答案．【详解】解：根据题意，如图：∵AB是的直径，OD是半径，，∴AE=CE，∴阴影CED的面积等于AED的面积，∴，∵，，∴，∴；故选：B【点睛】本题考查了求扇形的面积，垂径定理，解题的关键是掌握所学的知识，正确利用扇形的面积公式进行计算．3、B【分析】由切线的性质可推出，．再根据直角三角形全等的判定条件“HL”，即可证明，即得出．【详解】∵PA，PB是⊙O的切线，A，B为切点，∴，，∴在和中，，∴，∴．故选：B【点睛】本题考查切线的性质，三角形全等的判定和性质．熟练掌握切线的性质是解答本题的关键．4、C【分析】先设半径为r，再根据弧长公式建立方程，解出r即可【详解】设半径为r，则周长为2πr，120°所对应的弧长为解得r=3故选C【点睛】本题考查弧长计算，牢记弧长公式是本题关键．5、C【分析】根据中心对称图形的概念：一个平面图形绕某一点旋转180,如果旋转后的图形能够和原图形重合,那么这个图形叫做中心对称图形,这个点就是对称中心. 根据中心对称图形的概念对各选项进行一一分析判定即可求解．【详解】A、不是中心对称图形，不符合题意；B、不是中心对称图形，不符合题意；C、是中心对称图形，符合题意；D、不是中心对称图形，不符合题意．故选：C．【点睛】本题考查了中心对称图形，掌握好中心对称图形，中心对称图形是要寻找对称中心，旋转180度后能够与原来的图形重合．6、B【分析】由题意易得，然后根据三角形外角的性质可求解．【详解】解：由旋转的性质可得：，∴；故选B．【点睛】本题主要考查旋转的性质及三角形外角的性质，熟练掌握旋转的性质及三角形外角的性质是解题的关键．7、C【分析】如图所示，连接CP，由切线的性质和切线长定理得到∠CPO=90°，∠COP=45°，由此推出CP=OP=4，再根据勾股定理求解即可．【详解】解：如图所示，连接CP，∵OA，OB都是圆C的切线，∠AOB=90°，P为切点，∴∠CPO=90°，∠COP=45°，∴∠PCO=∠COP=45°，∴CP=OP=4，∴，故选C．【点睛】本题主要考查了切线的性质，切线长定理，等腰直角三角形的性质与判定，勾股定理，熟知切线长定理是解题的关键．8、D【分析】根据圆内接正六边形的性质可得△AOB是正三角形，由面积公式可求出半径．【详解】解：如图，由圆内接正六边形的性质可得△AOB是正三角形，过作于 设半径为r，即OA=OB=AB=r， OM=OA•sin∠OAB=， ∵圆O的内接正六边形的面积为（cm2）， ∴△AOB的面积为（cm2）， 即， ， 解得r=4， 故选：D．【点睛】本题考查正多边形和圆，作边心距转化为直角三角形的问题是解决问题的关键．9、A【分析】根据等边三角形的对称性判断即可．【详解】∵等边三角形是轴对称图形，但不是中心对称图形，∴B，C，D都不符合题意；故选：A．【点睛】本题考查了等边三角形的对称性，熟练掌握等边三角形的对称性是解题的关键．10、B【分析】先根据平行线的性质得∠ACC′=∠CAB=64°，再根据旋转的性质得∠CAC′等于旋转角，AC=AC′，则利用等腰三角形的性质得∠ACC′=∠AC′C=64°，然后根据三角形内角和定理可计算出∠CAC′的度数，从而得到旋转角的度数．【详解】解：∵CC′∥AB，∴∠ACC′=∠CAB=64°∵△ABC在平面内绕点A旋转到△AB′C′的位置，∴∠CAC′等于旋转角，AC=AC′，∴∠ACC′=∠AC′C=64°，∴∠CAC′=180°-∠ACC′-∠AC′C=180°-2×64°=52°，∴旋转角为52°．故选：B．【点睛】本题考查了旋转的性质：对应点到旋转中心的距离相等；对应点与旋转中心所连线段的夹角等于旋转角；旋转前、后的图形全等．二、填空题1、20【分析】先利用旋转的性质得到∠ADC=∠D=90°，∠DAD′=α，再利用四边形内角和计算出∠BAD‘=70°，然后利用互余计算出∠DAD′，从而得到α的值．【详解】∵矩形ABCD绕点A顺时针旋转到矩形A′B′C′D′的位置，∴∠ADC=∠D=90°，∠DAD′=α，∵∠ABC=90°，∴∠BAD’=180°-∠1=180°-110°=70°，∴∠DAD′=90°-70°=20°，即α=20°．故答案为20．【点睛】本题考查了旋转的性质：对应点到旋转中心的距离相等；对应点与旋转中心所连线段的夹角等于旋转角；旋转前、后的图形全等．2、        【分析】过O作OC垂直于弦AB，利用垂径定理得到C为AB的中点，然后由OA=OB，且∠AOB为直角，得到三角形OAB为等腰直角三角形，由斜边AB的长，利用勾股定理求出直角边OA的长即可；再由C为AB的中点，由AB的长求出AC的长，在直角三角形OAC中，由OA及AC的长，利用勾股定理即可求出OC的长，即为O点到AB的距离．【详解】解：过O作OC⊥AB，则有C为AB的中点，∵OA=OB，∠AOB=90°，AB=a，∴根据勾股定理得： OA2+OB2=AB，∴OA=，在Rt△AOC中，OA=，AC=AB=，根据勾股定理得：OC==．故答案为：；【点睛】此题考查了垂径定理，等腰直角三角形的性质，以及勾股定理，在圆中遇到弦，常常过圆心作弦的垂线，根据近垂径定理由垂直得中点，进而由弦长的一半，圆的半径及弦心距构造直角三角形，利用勾股定理来解决问题．3、40°度【分析】直接根据圆周角定理即可得出结论．【详解】解：与是同弧所对的圆心角与圆周角，，．故答案为：．【点睛】本题考查的是圆周角定理，解题的关键是熟知在同圆或等圆中，同弧或等弧所对的圆周角相等，都等于这条弧所对的圆心角的一半．4、【分析】根据圆锥的展开图为扇形，结合弧长公式、圆周长的求解公式、面积的求解公式，圆锥侧面积的求解公式可得出答案．【详解】解：圆锥的侧面展开图是一个扇形，扇形的半径等于圆锥的母线长，扇形的弧长等于圆锥的底面圆周长，故可得，这个扇形的半径为，扇形的弧长为，圆锥的侧面积为；圆锥的全面积为圆锥的底面积侧面积：．故答案为：．【点睛】本题考查了圆锥的计算，解题的关键是掌握圆锥侧面展开图是个扇形，要熟练掌握扇形与圆锥之间的联系，难度一般．5、3【分析】过A作AE⊥BC于E，过C作CF⊥AD于F，根据圆周角定理可得∠ACB=∠B=∠D，AB=AC=10，再由等腰三角形的性质可知BE=CE=6，根据相似三角形的判定证明△ABE∽△CDF，由相似三角形的性质和勾股定理分别求得AE、DF、CF， AF即可求解．【详解】解：过A作AE⊥BC于E，过C作CF⊥AD于F，则∠AEB=∠CFD=90°，∵＝， AB＝10，∴∠ACB=∠B=∠D，AB=AC=10，∵AE⊥BC，BC=12，∴BE=CE=6，  ∴，∵∠B=∠D，∠AEB=∠CFD=90°，∴△ABE∽△CDF，∴，∵AB=10，CD=5，BE=6，AE=8，∴，解得：DF=3，CF=4，在Rt△AFC中，∠AFC=90°，AC=10，CF=4，则，∴AD=DF+AF=3＋2，故答案为：3＋2．【点睛】本题考查圆周角定理、等腰三角形的性质、相似三角形的判定与性质、勾股定理，熟练掌握圆周角定理和相似三角形的判定与性质是解答的关键．三、解答题1、（1）见详解；（2）90，直径所对的圆周角是直角，BD．【分析】（1）根据作图步骤作出图形即可；（2）根据题意填空，即可求解．【详解】解：（1）如图，CH为△ABC中AB边上的高；（2）证明：∵是的直径，点，在上，∴___90_°．（__直径所对的圆周角是直角_）（填推理的依据）∴，．∴，_BD__是的两条高线．∵，所在直线交于点，∴直线也是的高所在直线．∴是中边上的高．故答案为：90，直径所对的圆周角是直角，BD．【点睛】本题考查了圆周角定理的推理，三角形的三条高线相交于一点等知识，熟知两个定理，并根据题意灵活应用是解题关键．2、（1）△ABC是等边三角形，证明见解析；（2）见解析【分析】（1）利用圆周角定理可得∠BAC=∠CPB，∠ABC=∠APC，而∠APC=∠CPB=60°，所以∠BAC=∠ABC=60°，从而可判断△ABC的形状；（2）如图所示，在PC取一点E使得AE=AP，先证明△APE是等边三角形，得到AP=PE，∠AEP=60°，可以推出∠AEC=∠APB，然后证明△APB≌△AEC得到BP=CE，即可证明PC=PE+CE=AP+BP．【详解】解：（1）△ABC是等边三角形．证明如下：由圆周角定理：∠BAC=∠CPB，∠ABC=∠APC∵∠APC＝∠CPB＝60°，∴∠BAC＝∠ABC＝60°，∴∠ACB＝180°－∠BAC－∠ABC＝180°－60°－60°＝60°．∴△ABC是等边三角形．（2）如图所示，在PC取一点E使得AE=AP，∵∠APE=60°，AP=AE，∴△APE是等边三角形，∴AP=PE，∠AEP=60°，∴∠AEC=120°，又∵∠APC＝∠CPB＝60°，∴∠APB=120°，∴∠AEC=∠APB，∵△ABC是等边三角形，∴AB=AC，又∵∠ABP=∠ACE，∴△APB≌△AEC（AAS），∴BP=CE，∴PC=PE+CE=AP+BP．【点睛】本题考查了圆周角定理、等边三角形的性质与判定，全等三角形的性质与判定，解题的关键是掌握圆周角定理，正确求出∠ABC=∠BAC=60°．3、（1）20°；（2）；（3）AF= CF+BF，理由见解析【分析】（1）由△ABC是等边三角形，得到AB=AC，∠BAC=∠ABC=60°，由折叠的性质可知，∠EAD=∠CAD=20°，AC=AE，则∠BAE=∠BAC-∠EAD-∠CAD=20°，AB=AE，，∠CBF=∠ABE-∠ABC=20°；（2）同（1）求解即可；（3）如图所示，将△ABF绕点A逆时针旋转60°得到△ACG，先证明△AEF≌△ACF得到∠AFE=∠AFC，然后证明∠AFE=∠AFC=60°，得到∠BFC=120°，即可证明F、C、G三点共线，得到△AFG是等边三角形，则AF=GF=CF+CG=CF+BF．【详解】解：（1）∵△ABC是等边三角形，∴AB=AC，∠BAC=∠ABC=60°，由折叠的性质可知，∠EAD=∠CAD=20°，AC=AE，∴∠BAE=∠BAC-∠EAD-∠CAD=20°，AB=AE，∴，∴∠CBF=∠ABE-∠ABC=20°；（2）∵△ABC是等边三角形，∴AB=AC,∠BAC=∠ABC=60°，由折叠的性质可知，，AC=AE，∴ ，AB=AE，∴，∴；（3）AF= CF+BF，理由如下：如图所示，将△ABF绕点A逆时针旋转60°得到△ACG，∴AF=AG，∠FAG=60°，∠ACG=∠ABF，BF=CG在△AEF和△ACF中，，∴△AEF≌△ACF（SAS），∴∠AFE=∠AFC，∵∠CBF+∠BCF+∠BFD+∠CFD=180°，∠CAF+∠CFA+∠ACD+∠CFD=180°，∴∠BFD=∠ACD=60°，∴∠AFE=∠AFC=60°，∴∠BFC=120°，∴∠BAC+∠BFC=180°，∴∠ABF+∠ACF=180°，∴∠ACG+∠ACF=180°，∴F、C、G三点共线，∴△AFG是等边三角形，∴AF=GF=CF+CG=CF+BF．【点睛】本题主要考查了等边三角形的性质与判定，旋转的性质，折叠的性质，全等三角形的性质与判定，三角形内角和定理，熟知相关知识是解题的关键．4、（1）是；（2）16°或24°或32°；（3）2或或；（4）．【分析】（1）根据幸运线定义即可求解；（2）分3种情况，根据幸运线定义得到方程求解即可；（3）根据幸运线定义得到方程求解即可；（4）利用时针1分钟走，分针1分钟走，可解答问题．【详解】解：（1）一个角的平分线是这个角的“幸运线”；故答案为：是；（2）①设∠AOC=x，则∠BOC=2x，由题意得，x+2x=48°，解得x=16°，②设∠AOC=x，则∠BOC=x，由题意得，x+x=48°，解得x=24°，③设∠AOC=x，则∠BOC=x，由题意得，x+x=48°，解得x=32°，故答案为：16°或24°或32°；（3）OB是射线OM与ON的幸运线，则∠BOM=∠MON，即50-10t=（50-10t+15t），解得t=2；∠BOM=∠MON，即50-10t=（50-10t+15t），解得t=；∠BOM=∠MON，即50-10t=（50-10t+15t），解得t=；故t的值是2或或；（4）时针1分钟走，分针1分钟走，设小丽帮妈妈取包裹用了x分钟，则有0.5x+3×30=6x，解得：x=．【点睛】本题考查了旋转的性质，幸运线定义，学生的阅读理解能力及知识的迁移能力．理解“幸运线”的定义是解题的关键．5、（1）见详解；（2）【分析】（1）连接OD，由题意易得，则有△ODB是等边三角形，然后可得△AEO也为等边三角形，进而可得OD∥AC，最后问题可求证；（2）由（1）易得AE=ED，∠CED=∠OBD=60°，然后可得圆O的半径，进而可得扇形OED和△OED的面积，则有弓形ED的面积，最后问题可求解．【详解】（1）证明：连接OD，如图所示：∵四边形BDEO是平行四边形，∴，∴△ODB是等边三角形，∴∠OBD=∠BOD=60°，∴∠AOE=∠OBD=60°，∵OE=OA，∴△AEO也为等边三角形，∴∠EAO=∠DOB=60°，∴AE∥OD，∴∠ODC+∠C=180°，∵CD⊥AE，∴∠C=90°，∴∠ODC=90°，∵OD是圆O的半径，∴CD是⊙O的切线．（2）解：由（1）得∠EAO=∠AOE=∠OBD=∠BOD=60°，ED∥AB，∴∠EAO=∠CED=60°，∵∠AOE+∠EOD+∠BOD=180°，∴∠EOD=60°，∴△DEO为等边三角形，  ∴ED=OE=AE，∵CD⊥AE，∠CED=60°，∴∠CDE=30°，∴，∵，∴，∴，设△OED的高为h，∴，∴，∴．【点睛】本题主要考查扇形面积公式、切线的判定定理及解直角三角形，熟练掌握扇形面积公式、切线的判定定理及解直角三角形是解题的关键．