辽宁省锦州市2021-2022学年八年级上学期期末数学试卷（word版 含答案）

这是一份辽宁省锦州市2021-2022学年八年级上学期期末数学试卷（word版 含答案），共29页。试卷主要包含了选择题，填空题，计算题，解答题等内容，欢迎下载使用。

1．（2分）在，，，中，最简二次根式是
A．B．C．D．
2．（2分）下列各组数中不能作为直角三角形三边长的是
A．1，2，3B．3，4，5C．5，12，13D．8，15，17
3．（2分）下列四个命题中，真命题是
A．如果，，那么
B．平面内点与点关于轴对称
C．三角形的一个外角大于这个三角形中的任何一个内角
D．三角形的任意两边之和一定大于第三边
4．（2分）在一次数学测验中，甲、乙、丙、丁四位同学的成绩（单位：分）分别是80，，80，70，若这四位同学成绩的众数与平均数恰好相等，则他们成绩的中位数是
A．90分B．85分C．80分D．75分
5．（2分）如图，将直角三角板的锐角顶点，分别放置在两条平行直线，上，若，则的度数是
A．B．C．D．
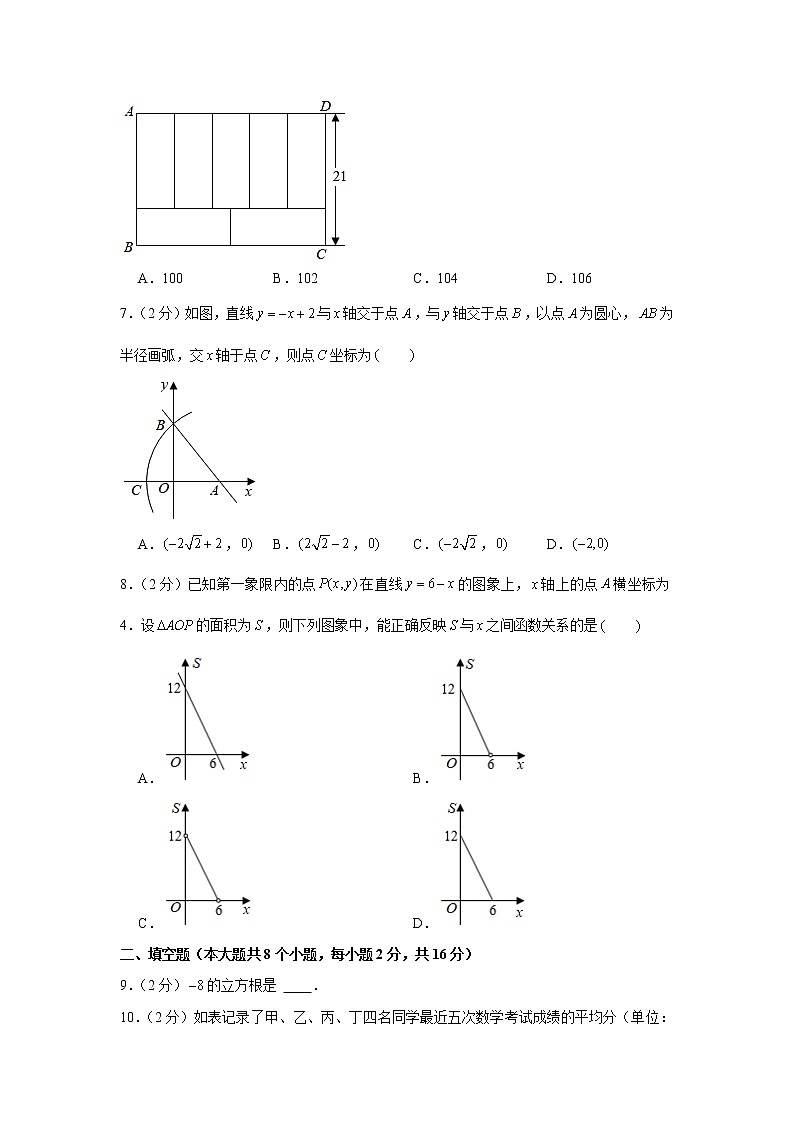
6．（2分）如图，七个相同的小长方形组成一个大长方形，若，则长方形的周长为
A．100B．102C．104D．106
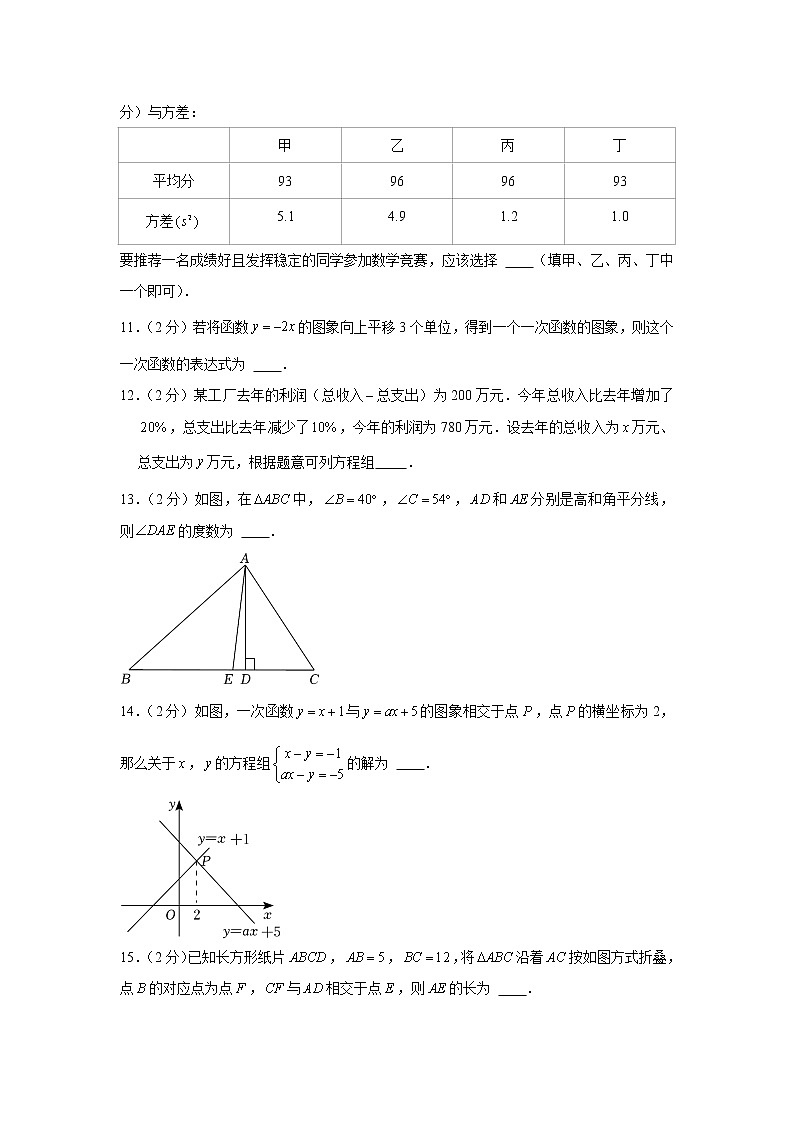
7．（2分）如图，直线与轴交于点，与轴交于点，以点为圆心，为半径画弧，交轴于点，则点坐标为
A．，B．，C．，D．
8．（2分）已知第一象限内的点在直线的图象上，轴上的点横坐标为4．设的面积为，则下列图象中，能正确反映与之间函数关系的是
A．B．
C．D．
二、填空题（本大题共8个小题，每小题2分，共16分）
9．（2分）的立方根是 ．
10．（2分）如表记录了甲、乙、丙、丁四名同学最近五次数学考试成绩的平均分（单位：分）与方差：
要推荐一名成绩好且发挥稳定的同学参加数学竞赛，应该选择 （填甲、乙、丙、丁中一个即可）．
11．（2分）若将函数的图象向上平移3个单位，得到一个一次函数的图象，则这个一次函数的表达式为 ．
12．（2分）某工厂去年的利润（总收入总支出）为200万元．今年总收入比去年增加了，总支出比去年减少了，今年的利润为780万元．设去年的总收入为万元、总支出为万元，根据题意可列方程组 ．
13．（2分）如图，在中，，，和分别是高和角平分线，则的度数为 ．
14．（2分）如图，一次函数与的图象相交于点，点的横坐标为2，那么关于，的方程组的解为 ．
15．（2分）已知长方形纸片，，，将沿着按如图方式折叠，点的对应点为点，与相交于点，则的长为 ．
16．（2分）平面直角坐标系中，点，，，和，，，分别在直线和轴上，△，△，△，都是等腰直角三角形，如果，则点的纵坐标是 ．
三、计算题（本大题共15分）
17．（15分）（1）计算：；
（2）计算：；
（3）用适当的方法解方程组：．
四、解答题（本大题共3个题，第18，19题各6分，第20题7分，共19分）
18．（6分）某校组织八年级全体200名学生参加“强国有我”读书活动，要求每人必读本书，活动结束后从八年级学生中随机抽查了若干名学生了解读书数量情况，并根据本；本；本；本四种类型的人数绘制了不完整的条形统计图（图和扇形统计图（图．请根据统计图解答下列问题：
（1）在这次调查中类型有多少名学生？
（2）直接写出被调查学生读书数量的众数和中位数；
（3）求被调查学生读书数量的平均数，并估计八年级200名学生共读书多少本？
19．（6分）如图，直线与轴，轴分别交于，两点．
（1）求的面积；
（2）在轴上有一定点，在轴上有一动点，若与面积相等，请直接写出点的坐标．
20．（7分）请将下列题目中横线上的证明过程和依据补充完整：
如图，点在上，，平分，，于点．求证：．
证明：，

，
，
即，
平分，

．

．
，
．
．
五、解答题（本大题共2个题，每题8分，共16分）
21．（8分）2022年北京冬奥会期间体育中心将举行短道速滑比赛，观看短道速滑比赛的门票分为两种：种门票600元张，种门票120元张．某旅行社为一个旅行团代购部分门票，若旅行社购买，两种门票共15张，总费用5160元，求旅行社为这个旅行团代购的种门票和种门票各多少张？（要求列方程组解答）
22．（8分）已知，两地间某道路全程为，甲、乙两车沿此道路分别从，两地同时出发匀速相向而行，甲车从地出发行驶后因有事按原路原速返回地，结果两车同时到达地．已知甲、乙两车距地的路程与甲车出发所用的时间的函数关系如图所示，请结合图象信息解答下列问题：
（1）甲车的速度为 ，乙车的速度为 ；
（2）求甲车出发多长时间两车途中首次相遇？
（3）直接写出甲车出发多长时间两车相距．
六、解答题（本大题共2个题，每题9分，共18分）
23．（9分）【概念认识】
如图①，在中，若，则，叫做的“三分线”．其中，是“邻三分线”， 是“邻三分线”．
【问题解决】
（1）如图②，在中，，，若的邻三分线交于点，则的度数为 ；
（2）如图③，在中，，分别是邻三分线和邻三分线，且，求的度数；
【延伸推广】
（3）在中，是的外角，的邻三分线所在的直线与的三分线所在的直线交于点．若，，直接写出的度数．（用含的代数式表示）
24．（9分）如图，在平面直角坐标系中有，，，作轴于点，轴于点，点的坐标为．
（1）请直接写出点的坐标；
（2）求直线的表达式；
（3）若为的中点，连接，动点从点出发，沿射线方向运动，当最大时，求点的坐标．
参考答案与解析
一、选择题（在每小题给出的四个选项中，只有一项是符合题目要求的；本大题共8个小题，每小题2分，共16分）
1．（2分）在，，，中，最简二次根式是
A．B．C．D．
【分析】根据最简二次根式的定义判断即可．
【解答】解：，故不符合题意；
是最简二次根式，故符合题意；
．，故不符合题意；
，故不符合题意；
故选：．
2．（2分）下列各组数中不能作为直角三角形三边长的是
A．1，2，3B．3，4，5C．5，12，13D．8，15，17
【分析】先求出两小边的平方和，再求出最长边的平方，最后看看是否相等即可．
【解答】解：、，故不是直角三角形，符合题意；
、，故是直角三角形，不符合题意；
、，故是直角三角形，不符合题意；
、，故是直角三角形，不符合题意；
故选：．
3．（2分）下列四个命题中，真命题是
A．如果，，那么
B．平面内点与点关于轴对称
C．三角形的一个外角大于这个三角形中的任何一个内角
D．三角形的任意两边之和一定大于第三边
【分析】利用不等式的性质、关于坐标轴对称的点的坐标特点、三角形的外角的性质及三角形的三边关系分别判断后即可确定正确的选项．
【解答】解：、如果，，那么可能，故原命题错误，是假命题，不符合题意；
、平面内点与点关于轴对称，故原命题错误，是假命题，不符合题意；
、三角形的一个外角大于任何一个不相邻的内角，故原命题错误，是假命题，不符合题意；
、三角形的任意两边之和一定大于第三边，正确，是真命题，符合题意．
故选：．
4．（2分）在一次数学测验中，甲、乙、丙、丁四位同学的成绩（单位：分）分别是80，，80，70，若这四位同学成绩的众数与平均数恰好相等，则他们成绩的中位数是
A．90分B．85分C．80分D．75分
【分析】因为的值不确定，所以众数也不能直接确定，需分类讨论：①；②；③且，再分别进行解答即可．
【解答】解：①时，众数是80，平均数，则此情况不成立，
②时，众数是80和70，而平均数是一个数，则此情况不成立，
③且时，众数是80，根据题意得：
，
解得，
则中位数是．
故选：．
5．（2分）如图，将直角三角板的锐角顶点，分别放置在两条平行直线，上，若，则的度数是
A．B．C．D．
【分析】延长交直线于点，由平行线的性质可得，则可求的度数．
【解答】解：延长交直线于点，如图，
，，
，
，
．
故选：．
6．（2分）如图，七个相同的小长方形组成一个大长方形，若，则长方形的周长为
A．100B．102C．104D．106
【分析】由图可看出本题的等量关系：小长方形的长小长方形的宽；小长方形的长宽，据此可以列出方程组求解．
【解答】解：设小长方形的长为，宽为．
由图可知：
解得．，
所以长方形的长为，宽为21，
长方形的周长为，
故选：．
7．（2分）如图，直线与轴交于点，与轴交于点，以点为圆心，为半径画弧，交轴于点，则点坐标为
A．，B．，C．，D．
【分析】利用一次函数图象上点的坐标特征可求出点，的坐标，利用勾股定理求出的长度，再结合点的坐标即可找出点的坐标．
【解答】解：当时，，
点的坐标为，；
当时，，解得：，
点的坐标为，．
，
点的坐标为，．
故选：．
8．（2分）已知第一象限内的点在直线的图象上，轴上的点横坐标为4．设的面积为，则下列图象中，能正确反映与之间函数关系的是
A．B．
C．D．
【分析】根据第一象限内的点在直线的图象上，轴上的点横坐标为4，从而可以得到关于的函数关系式，从而可以解答本题．
【解答】解：第一象限内的点在直线的图象上，轴上的点横坐标为4，
，，
，
故选：．
二、填空题（本大题共8个小题，每小题2分，共16分）
9．（2分）的立方根是 ．
【分析】利用立方根的定义即可求解．
【解答】解：，
的立方根是．
故答案为：．
10．（2分）如表记录了甲、乙、丙、丁四名同学最近五次数学考试成绩的平均分（单位：分）与方差：
要推荐一名成绩好且发挥稳定的同学参加数学竞赛，应该选择 丙 （填甲、乙、丙、丁中一个即可）．
【分析】首先比较平均数，平均数相同时选择方差较小的参加竞赛．
【解答】解：甲和丁的平均数较小，
从乙和丙中选择一人参加竞赛，
丙的方差较小，
选择丙竞赛．
故答案为：丙．
11．（2分）若将函数的图象向上平移3个单位，得到一个一次函数的图象，则这个一次函数的表达式为 ．
【分析】根据函数图象平移的法则“上加下减”，就可以求出平移以后函数的解析式，
【解答】解：将正比例函数的图象向上平移3个单位长度，得到一次函数的表达式为：，
故答案为：．
12．（2分）某工厂去年的利润（总收入总支出）为200万元．今年总收入比去年增加了，总支出比去年减少了，今年的利润为780万元．设去年的总收入为万元、总支出为万元，根据题意可列方程组 ．
【分析】设去年的总收入为万元、总支出为万元，根据去年的利润（总收入总支出）为200万元，今年的利润为780万元，列方程组即可．
【解答】解：设去年的总收入为万元、总支出为万元，
由题意得，．
故答案为：．
13．（2分）如图，在中，，，和分别是高和角平分线，则的度数为 ．
【分析】先根据三角形的内角和定理得到的度数，再利用角平分线的性质可求出，而，然后利用进行计算即可．
【解答】解：在中，
，
是的角平分线，
，
是的高，
在中，，
．
14．（2分）如图，一次函数与的图象相交于点，点的横坐标为2，那么关于，的方程组的解为 ．
【分析】利用方程组的解就是两个相应的一次函数图象的交点坐标进行判断．
【解答】解：把代入得，，
一次函数与的图象相交于点，则关于，的方程组的解为，
故答案为：．
15．（2分）已知长方形纸片，，，将沿着按如图方式折叠，点的对应点为点，与相交于点，则的长为 ．
【分析】由矩形的性质可得，，，根据平行线的性质和折叠的性质可得，即，根据勾股定理列方程可求的长．
【解答】解：四边形是矩形，
，，，
，
由折叠可得，
，
，
在中，，
即，
解得，
故答案为：．
16．（2分）平面直角坐标系中，点，，，和，，，分别在直线和轴上，△，△，△，都是等腰直角三角形，如果，则点的纵坐标是 ．
【分析】利用待定系数法可得、、的坐标，进而得出各点的坐标的规律．
【解答】解：，
设，则，
解得，
，
设，则有，
解得，
，
由此发现点的纵坐标为，
即点的纵坐标是，
故答案为：．
三、计算题（本大题共15分）
17．（15分）（1）计算：；
（2）计算：；
（3）用适当的方法解方程组：．
【分析】（1）原式各自化简后，合并同类项即可得到结果；
（2）原式利用完全平方公式化简，去括号合并即可得到结果；
（3）方程组利用加减消元法求出解即可．
【解答】解：（1）原式
；
（2）原式
；
（3），
①②得：，
解得：，
把代入②得：，
解得：，
则方程组的解为．
四、解答题（本大题共3个题，第18，19题各6分，第20题7分，共19分）
18．（6分）某校组织八年级全体200名学生参加“强国有我”读书活动，要求每人必读本书，活动结束后从八年级学生中随机抽查了若干名学生了解读书数量情况，并根据本；本；本；本四种类型的人数绘制了不完整的条形统计图（图和扇形统计图（图．请根据统计图解答下列问题：
（1）在这次调查中类型有多少名学生？
（2）直接写出被调查学生读书数量的众数和中位数；
（3）求被调查学生读书数量的平均数，并估计八年级200名学生共读书多少本？
【分析】（1）由两个统计图可知，类人数为8人，占可得抽查总人数，进而求出类的学生人数；
（2）根据中位数、众数的意义求解即可；
（3）先求出样本的平均数，再乘以总人数即可．
【解答】解：（1）这次调查一共抽查植树的学生人数为（人，
类人数（人；
（2）被调查学生读书数量的众数为2本，中位数为2本；
（3）被调查学生读书数量的平均数为：（本，
（本，
估计八年级200名学生共读书460本．
19．（6分）如图，直线与轴，轴分别交于，两点．
（1）求的面积；
（2）在轴上有一定点，在轴上有一动点，若与面积相等，请直接写出点的坐标．
【分析】（1）由直线求得、的坐标，然后根据三角形面积公式即可求得的面积；
（2）利用三角形面积求得，进而即可求得的坐标．
【解答】解：（1）函数，当时，，
；
当时，，
，
，，
；
（2）点，
，
与面积相等，
，即，
，
点坐标为或．
20．（7分）请将下列题目中横线上的证明过程和依据补充完整：
如图，点在上，，平分，，于点．求证：．
证明：，
两直线平行，内错角相等
，
，
即，
平分，

．

．
，
．
．
【分析】根据平行线性质与判定、角平分线定义、垂直的定义填空即可．
【解答】证明：，
两直线平行，内错角相等），
，
，
即，
平分，
角平分线的定义），
．
内错角相等，两直线平行），
．
，
垂直的定义）．
．
故答案为：两直线平行，内错角相等；角平分线的定义；；内错角相等，两直线平行；；；垂直的定义．
五、解答题（本大题共2个题，每题8分，共16分）
21．（8分）2022年北京冬奥会期间体育中心将举行短道速滑比赛，观看短道速滑比赛的门票分为两种：种门票600元张，种门票120元张．某旅行社为一个旅行团代购部分门票，若旅行社购买，两种门票共15张，总费用5160元，求旅行社为这个旅行团代购的种门票和种门票各多少张？（要求列方程组解答）
【分析】设旅行社为这个旅行团代购种门票张，种门票张，利用总价单价数量，结合“旅行社购买，两种门票共15张，总费用5160元”，即可得出关于，的二元一次方程组，解之即可得出结论．
【解答】解：设旅行社为这个旅行团代购种门票张，种门票张，
依题意得：，
解得：．
答：旅行社为这个旅行团代购种门票7张，种门票8张．
22．（8分）已知，两地间某道路全程为，甲、乙两车沿此道路分别从，两地同时出发匀速相向而行，甲车从地出发行驶后因有事按原路原速返回地，结果两车同时到达地．已知甲、乙两车距地的路程与甲车出发所用的时间的函数关系如图所示，请结合图象信息解答下列问题：
（1）甲车的速度为 80 ，乙车的速度为 ；
（2）求甲车出发多长时间两车途中首次相遇？
（3）直接写出甲车出发多长时间两车相距．
【分析】（1）直接利用图象求出速度和时间即可；
（2）分别求出甲、乙两车距地的路程与甲车出发所用的时间的函数关系式，再列方程解答即可；
（3）分相遇前和相遇后两种情况进行讨论即可．
【解答】解：（1）由题意可知，甲车的速度为：，乙车的速度为：；
故答案为：80；60；
（2）设，
将代入得，
，
设，
将，代入得：
，解得：，
，
，
解得：，
甲车出发两车途中首次相遇；
（3）①相遇前，
设甲车出发小时两车相距40千米，
则，，
解得；
②相遇后，
由图象可知：甲车行驶时，甲车与乙车的距离最大，
此时乙行驶的路程为（千米），
甲乙两车的最大距离为（千米），
甲车出发两车相距40千米，
综上所述，甲车出发或两车相距40千米．
六、解答题（本大题共2个题，每题9分，共18分）
23．（9分）【概念认识】
如图①，在中，若，则，叫做的“三分线”．其中，是“邻三分线”， 是“邻三分线”．
【问题解决】
（1）如图②，在中，，，若的邻三分线交于点，则的度数为 ；
（2）如图③，在中，，分别是邻三分线和邻三分线，且，求的度数；
【延伸推广】
（3）在中，是的外角，的邻三分线所在的直线与的三分线所在的直线交于点．若，，直接写出的度数．（用含的代数式表示）
【分析】（1）根据题意可是“邻三分线”可求得的度数，再利用三角形外角的性质可求解；
（2）结合（1）根据、分别是邻三分线和邻三分线，且，即可求的度数；
（3）分2种情况进行画图计算：情况一：如图，当和分别是“邻三分线”、“邻三分线”时，可得，可求解；情况二：如图，当和分别是“邻三分线”、“邻三分线”时，可得可求解．
【解答】解：（1）的邻三分线交于点，，
，
，
，
故答案为：；
（2）在中，，
，
又、分别是邻三分线和邻三分线，
，，
，
，
，
在中，
；
（3）如图，当和分别是“邻三分线”、“邻三分线”时，
，，，
，
即，
，，
；
如图，当和分别是“邻三分线”、“邻三分线”时，
，，，
，
即，
，，
．
综上所述：的度数为：或．
24．（9分）如图，在平面直角坐标系中有，，，作轴于点，轴于点，点的坐标为．
（1）请直接写出点的坐标；
（2）求直线的表达式；
（3）若为的中点，连接，动点从点出发，沿射线方向运动，当最大时，求点的坐标．
【分析】（1）证明，即可求点的坐标；
（2）由待定系数法求解析式即可；
（3）延长交射线于点，则点为所求；延长交射线于点，可证，由全等得到，求出直线的直线解析式为，直线的解析式为，两直线的交点即为．
【解答】解：（1）轴，轴，
，
，
，，
，
，
，
，，
点的坐标为，
，，
；
（2）设直线的解析式为，
，
，
；
（3）延长交射线于点，则点为所求；
延长交射线于点，
，
，，
点为中点，
，
，
，
，
，，
设直线的解析式为，
，
，
直线的直线解析式为，
设直线的解析式为，
，
直线的解析式为，
，
解得，
，．
甲
乙
丙
丁
平均分
93
96
96
93
方差
5.1
4.9
1.2
1.0
甲
乙
丙
丁
平均分
93
96
96
93
方差
5.1
4.9
1.2
1.0