模板02 代数式及其运算专项练习-备战2022年中考数学专项解题方法归纳探究(全国通用)
展开
这是一份模板02 代数式及其运算专项练习-备战2022年中考数学专项解题方法归纳探究(全国通用),文件包含模板02代数式及其运算专项练习解析版docx、模板02代数式及其运算专项练习原卷版docx等2份试卷配套教学资源,其中试卷共20页, 欢迎下载使用。
模板2代数式及其运算专项练习一、选择题1.(2021·浙江九年级二模)下列计算正确的是( )A. B. C. D.【答案】D【详解】解:A. ,故本选项错误; B. ,故本选项错误;C. ,故本选项错误; D. ,故本选项正确.故选D.2.(2021·江门市第二中学九年级二模)下列运算正确的是( )A.+= B.4×3=12 C.x5•x6= D.(x2)5=【答案】C【详解】解:A、与不是同类二次根式,不能合并,故A选项错误;B、4×3=12a,故B选项错误;C、x5•x6=,故C选项正确;D、(x2)5=,故D选项错误,故选:C.3.(2021·江苏九年级月考)下列计算正确的是( )A. B.C. D.【答案】D【详解】A.,故该选项计算错误,不符合题意,B.,故该选项计算错误,不符合题意,C.+=,故该选项计算错误,不符合题意,D.,故该选项计算正确,符合题意,故选:D.4.(2021·内蒙古呼伦贝尔·)下列计算正确的是( )A. B. C. D.【答案】A【详解】A:,符合题意.B:,不符合题意.C:,不符合题意.D:,不符合题意.故选:A.5.(2020·湖南邵阳·中考真题)下列计算正确的是( )A. B.C. D.【答案】D【详解】解:A. ,故A选项错误;B. ,故B选项错误;C. ,故C选项错误; D. ,故D选项正确.故答案为D.6.(2019·重庆中考真题)按如图所示的运算程序,能使输出y值为1的是( )A. B. C. D.【答案】D【详解】解:A选项满足m≤n,则y=2m+1=3; B选项不满足m≤n,则y=2n-1=-1; C选项满足m≤n,则y=2m-1=3; D选项不满足m≤n,则y=2n-1=1; 故答案为D;7.(2021·上海九年级专题练习)关于代数式,有以下几种说法,①当时,则的值为-4.②若值为2,则.③若,则存在最小值且最小值为0.在上述说法中正确的是( )A.① B.①② C.①③ D.①②③【答案】C【详解】解:①当时,.故①正确;②若值为2,则,∴a2+2a+1=2a+4,∴a2=3,∴.故②错误;③若a>-2,则a+2>0,∴===≥0.∴若a>-2,则存在最小值且最小值为0.故③正确.综上,正确的有①③.故选:C.8.(2020·安徽九年级其他模拟)化简二次根式 的结果是( )A. B.- C. D.-【答案】B【详解】故选B二、填空题9.(2021·甘肃九年级二模)有一个数值转换器的原理如图所示,若开始输入x的值是,可发现第1次输出的结果是,第2次输出的结果是1,第3次输出的结果是,依次继续下去…,第2021次输出的结果是________.【答案】-1【详解】解:第4次输出的结果是2,第5次输出的结果是-1,第6次输出的结果是1,第7次输出的结果是-2,第8次输出的结果是2,第9次输出的结果是-1,所以,从第5次开始,每4次输出为一个循环组依次循环,(2021-4)÷4=504…1,所以,第2021次输出的结果是-1.故答案为:-1.10.(2019·广东九年级一模)已知与是同类项,求________.【答案】0或124【详解】解:∵与是同类项,∴且 解得,a=0或4,此时,b=1或3;,当a=0时,原式=; 当a=4时,原式=; 故答案为:0或12411.(2021·苏州市立达中学校九年级二模)式子有意义,则a的取值范围是_________.【答案】a≥1且a≠2【详解】解:由题意得a﹣1≥0且a﹣2≠0,解得a≥1且a≠2,故答案为:a≥1且a≠2.12.(2018·山东中考模拟)化简:(a+2+)=_______.【答案】2a﹣6【详解】原式= = ==2(a﹣3)=2a﹣6.故答案为2a﹣6.三、解答题13.(2021·山东九年级二模)实际问题:有支队伍,每支队伍都有足够多的水平完全相同的队员,要从这支队伍中抽调部分队员安排到一张有四个位置的方桌进行竞技比赛,四个位置可以出现来自于同一队伍的队员,为了防止他们作弊,需要避免同队的队员坐在相邻的座位上.那么一共有多少种不同的安排方法?问题探究:探究一:如果有两支队伍参赛,要求相邻的座位不能安排同一队的队员,那么共有多少种不同的安排方法?不妨设两支队伍分别为.从①号位开始,我们有2种选择,即队员或队员,②③号位置都只有1种选择(另一支队伍的队员).④号位也只有1种选择.这样就得到了,一共有两种不同的安排方法.探究二:如果有三支队伍参赛,要求相邻的座位不能安排同一队的队员,那么共有多少种不同的安排方法?不妨设三支队伍分别为.让我们运用上面的方法试试①号位置有3种队员可以选择,即队员、队员或队员,②③两个位置选择队员时,我们需要考虑两种不同的情形:第一种:若②③号位队员来自于同一队伍,则②号位有2种选择,③号只有1种选择,④号位会有2中选择,此时会有种安排方法;第二种:若②③号位队员来自于不同的队伍,则②号位有2种选择,③号位只有1种选择,④号位也只有1种选择,此时会有种安排方法.把上述两种情况的结果加起来得到12+6=18,一共有18种不同的安排方法.探究三:如果有四支队伍参赛,要求相邻的座位不能安排同一队的队员,那么共有多少种不同的安排方法?(请按照前面的探究方法,描述如果有四支参赛队伍时,会有多少种结果的推算过程)归纳探究:如果有支队伍参赛,要求相邻的座位不能安排同一队的队员,那么共有多少种不同的安排方法?无论有多少支参赛队伍,我们都要考虑两种情况:②③号位队员来自于同一个队伍;②③号位队员来自于不同的队伍.(1)如果有支参赛队伍,①号位有 种队员可以选择,②号位有 种队员可以选择.(2)若②③号位队员来自于同一队伍,则③号位只有1种选择,④号位有 种选择,这样我们就有 种安排方法(结果不需化简);(3)若②③号位队员来自不同队伍,则③号位有 种选择,④号位有 种选择,这样我们就有 种安排方法.(结果不需化简)(4)如果有支队伍参赛,要求相邻的座位不能安排同一队的队员,那么共有 种不同的安排方法.(结果不需化简)【答案】探究三:48种;归纳探究:(1);;(2);;(3);;;(4)【详解】解:不妨设为四支队伍,让我们运用上在的方法试试,①号位置有4种队员可以选择,即队员、队员或队员或 队员,②③两个位置选择队员时,我们需要考虑两种不同的情形:第一种:②③号位队员来自于同一队伍,②号位有3种选择,那么③号位与②号位队友相同,所以③号只有1种选择,④号位就会有3种选择,此时会有:种安排方法;第二种:若②③号位队员来自于不同的队伍,②号位有3种选择,那么③号位与②号位队员不同,③号位只有2种选择,那么④号位只有2种选择,此时会有种安排方法.把上述两种情况的结果加起来得到36+48=84,一共有84种不同的安排方法.归纳探究:如果有支队伍参赛,要求相邻的座位不能安排同一队伍的队员,那么有多少种不同的安排方法呢?无论有多少支参赛队伍,我们都要考虑两种情况:②③号位队员来自于同一个队伍;②③号位队员来自于不同的队伍.(1)如果有支参赛队伍,①号位有种队员可以选择,②号位有种队员可以选择;(2)若②③号位队员来自于同一队伍,则③号位只有1种选择,这样,④号位有种选择,这样我们就有种安排方法(结果不需要化简);(3)若②③号位队员来自于不同队伍,则③号位有种选择,④号位有种不同的队员可以选择,这样我们就有 种安排方法(结果不需要化简);(4)如果有支队伍参赛,要求相邻的座位不能安排同一队伍的队员,那么把(2)、(3)种情况的结果加起来得到有:种安排方法.14.(2019·山西)观察下列各式及证明过程:①;②;③.验证:;.(1)按照上述等式及验证过程的基本思想,猜想的变形结果,并进行验证;(2)针对上述各式反映的规律,写出用(为正整数,且)表示的等式.【答案】(1),验证见解析;(2)(为正整数,).【详解】解:(1)猜着:验证:;(2)(为正整数,).15.(2021·重庆一中)材料一:对于一个四位数,若满足千位数字与十位数字的和等于百位数字与个位数字的和,则称这个数为“间位等和数”,例如:,∵,∴5247是“间位等和数”;,∵,∴3145不是“间位等和数”材料二:将一个四位数千位上的数字与百位上的数字对调,十位上的数字与个位上的数字对调后可以得到一个新的四位 数,记.例如,对调千位上的数字与百位上的数字及十位上的数字与个位上的数字得到2574,所以.(1)判断3564和1572是否为“间位等和数”,并说明理由;(2)若和都是“间位等和数”,其中,(,,,且,,,均为整数),规定:,若,求的最小值.【答案】(1)3564是“间位等和数”, 1572不是“间位等和数”;(2)0【详解】解:(1)是“间位等和数”;,不是“间位等和数”;(2),其千位数为5,百位数为,十位数为4,个位数为b,,即,,其千位数为x,百位数为3,十位数为,个位数为2,,即,,,解得:,则由或或,对应的y和b的值分别为:;;,,,,且,,,均为整数,以上情况均符合,,则k的值分别为;;,故k的最小值为:0.16.(2021·安徽)观察以下等式:第1个等式:42+32=52;第2个等式82+152=172;第3个等式:122+352=372;第4个等式:162+632=652;……;按照以上规律,解决下列问题:(1)写出第5个等式: ;(2)写出你猜想的第n个等式: ______(用含n的等式表示),并证明.【答案】(1)202+992=1012; (2)(4n)2+[(2n-1)(2n+1)]2=[(2n-1)(2n+1)+2]2;证明见解析.【详解】解:(1)观察等式中的3个数中的数字与等式的序号的关系,第一个数是序号的4倍的平方,第二个数是从1开始的连续两个奇数的乘积的平方,第三个数是连续两个奇数乘积+2的平方,∴第5个等式为(4×5)2+[9×11]2=202+992=1012; 故答案为202+992=1012;(2)依据(1)中找到的规律得到第n个式子为:(4n)2+[(2n-1)(2n+1)]2=[(2n-1)(2n+1)+2]2;证明:左边=16n2+16n4-8n2+1=(4n2+1)2;右边=(4n2+1)2;∴左=右,即原等式成立.17.(2021·河北九年级专题练习)概念学习规定:求若干个相同的实数(均不为0)的除法运算叫做除方,如,类比实数的乘方,我们把记作,读作“2的圈3次方”,一般地,把个相除记作,读作“的圈次方”初步探究计算:(1);(2).深入思考我们知道,实数的减法运算可以转化为加法运算,除法运算可以转化为乘法运算,实数的除方也可以按照下面的方法转化为乘方运算.例如:.参考上面的方法,完成下列各题:(3)计算: , ;(4)已知:,求的值.【答案】(1);(2);(3),2;(4)【详解】初步探究:(1);故答案为;(2);故答案为;深入思考:(3)故答案为;2.(4)由已知得,,∴,即,∴,∴.18.(2021·陕西西北工业大学附属中学九年级其他模拟)先化简,再求值:(﹣)÷,其中a=.【答案】原式=【详解】原式===,当a=时,原式=.19.(2021·四川省内江市第六中学九年级一模)观察下面的式子:S1=1+,S2=1+,S3=1+…Sn=1+(1)计算:= ,= ;猜想= (用n的代数式表示);(2)计算:S=(用n的代数式表示).【答案】(1) ;(2)【详解】(1)∵S1=1+ ,∴;∵S2=1+,∴;∵S3=1+,∴;∵Sn=1+,∴;(2)解:S= = = =20.(2021·河南九年级一模)下面是小彬同学进行分式化简的过程,请认真阅读并完成相应任务.…第一步…第二步…第三步…第四步…第五步…第六步任务一:填空:①以上化简步骤中,第一步进行的运算是( )A.整式乘法 B.因式分解②第______步开始出现错误,这一步错误的原因是______;任务二:请直接写出该分式化简的正确结果;任务三:除纠正上述错误外,请根据平时的经验,就分式的化简过程写出一条注意事项.【答案】任务一:①;②三;分式相加时,没有对1通分(答案不唯一,合理即可);任务二:2;任务三:答案不唯一,见解析.【详解】任务一:①是进行了因式分解,故选:B②三;分式相加时,没有对1通分(答案不唯一,合理即可);故答案为:三;分式相加时,没有对1通分 =2故答案为:任务二:2任务三:答案不唯一,如:最后结果应化为最简分式或整式:括号前是“-”号,去掉括号后,括号里的各项均要变号;分式化简不能与解分式方程混淆等.
相关试卷
这是一份模板01 实数及其运算专项练习-备战2022年中考数学专项解题方法归纳探究(全国通用),文件包含模板01实数及其运算专项练习解析版docx、模板01实数及其运算专项练习原卷版docx等2份试卷配套教学资源,其中试卷共13页, 欢迎下载使用。
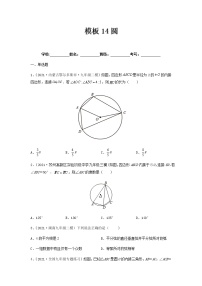
这是一份模板14 圆专项练习-备战2022年中考数学专项解题方法归纳探究(全国通用).,文件包含模板14圆原卷版docx、模板14圆解析版docx等2份试卷配套教学资源,其中试卷共36页, 欢迎下载使用。
这是一份模板15 统计与概率专项练习-备战2022年中考数学专项解题方法归纳探究(全国通用).,文件包含模板15统计与概率原卷版docx、模板15统计与概率解析版docx等2份试卷配套教学资源,其中试卷共23页, 欢迎下载使用。