

2021届江西省九江市高考数学二模试卷(理科)(含答案)
展开2021年江西省九江市高考数学二模试卷(理科)
一、选择题(每小题5分).
1.已知集合M={x|x2﹣5x﹣6<0},N={x|lnx>0},则M∩N=( )
A.{x|0<x<1} B.{x|1<x<6} C.{x|1<x<3} D.{x|2<x<3}
2.已知复数z=,则|z|=( )
A.0 B. C.2 D.﹣2
3.已知等差数列{an}的前n项和为Sn,且满足a3=7,S10=20,则a8=( )
A.﹣5 B.﹣3 C.3 D.5
4.若实数x,y满足,则z=x﹣2y的最小值为( )
A.﹣6 B.﹣1 C.2 D.6
5.将函数f(x)=cosx图象上所有点的横坐标都缩短到原来的,再向左平移个单位,得到函数g(x)的图象,则g(x)是( )
A.周期为4π的奇函数 B.周期为4π的偶函数
C.周期为π的奇函数 D.周期为π的偶函数
6.恩格尔系数(Engel'sCoefficien)是食品支出总额占个人消费支出总额的比重.居民可支配收入是居民可用于最终消费支出和储蓄的总和,即居民可用于自由支配的收入.如图为我国2013年至2019年全国恩格尔系数和居民人均可支配收入的折线图.
给出三个结论:
①恩格尔系数与居民人均可支配收入之间存在负相关关系;
②一个国家的恩格尔系数越小,说明这个国家越富裕;
③一个家庭收入越少,则家庭收入中用来购买食品的支出所占的比重就越小.
其中正确的是( )
A.① B.② C.①② D.②③
7.如图所示,四边形ABCD是边长为2的菱形,E是边BC上靠近C的三等分点,F为CD的中点,则=( )
A.2 B. C. D.﹣2
8.已知抛物线E:y2=2px(p>0),斜率为1的直线l过抛物线E的焦点,若抛物线E上有且只有三点到直线l的距离为,则p=( )
A.4 B.2 C.1 D.
9.古希腊毕达哥拉斯学派认为数是万物的本源,因此极为重视数的理论研究,他们常把数描绘成沙滩上的沙粒或小石子,并将它们排列成各种形状进行研究.形数就是指平面上各种规则点阵所对应的点数,是毕哥拉斯学派最早研究的重要内容之一.如图是三角形数和四边形数的前四个数,若三角形数组成数列{an},四边形数组成数列{bn},记cn=,则数列{cn}的前10项和为( )
A. B. C. D.
10.如图所示,在棱长为2的正方体ABCD﹣A1B1C1D1中,点E,F,G,H,I,J分别是棱A1B1,A1D1,DD1,CD,BC,BB1的中点,现在截面EFGHIJ内随机取一点M,则此点满足|AM|+|MC1|≤4的概率为( )
A. B. C. D.
11.若不等式xm(ex+x)≤emx+mxm(x﹣lnx)恒成立,则实数m的取值范围是( )
A.[,+∞) B.[1,+∞) C.[,+∞) D.[e﹣1,+∞)
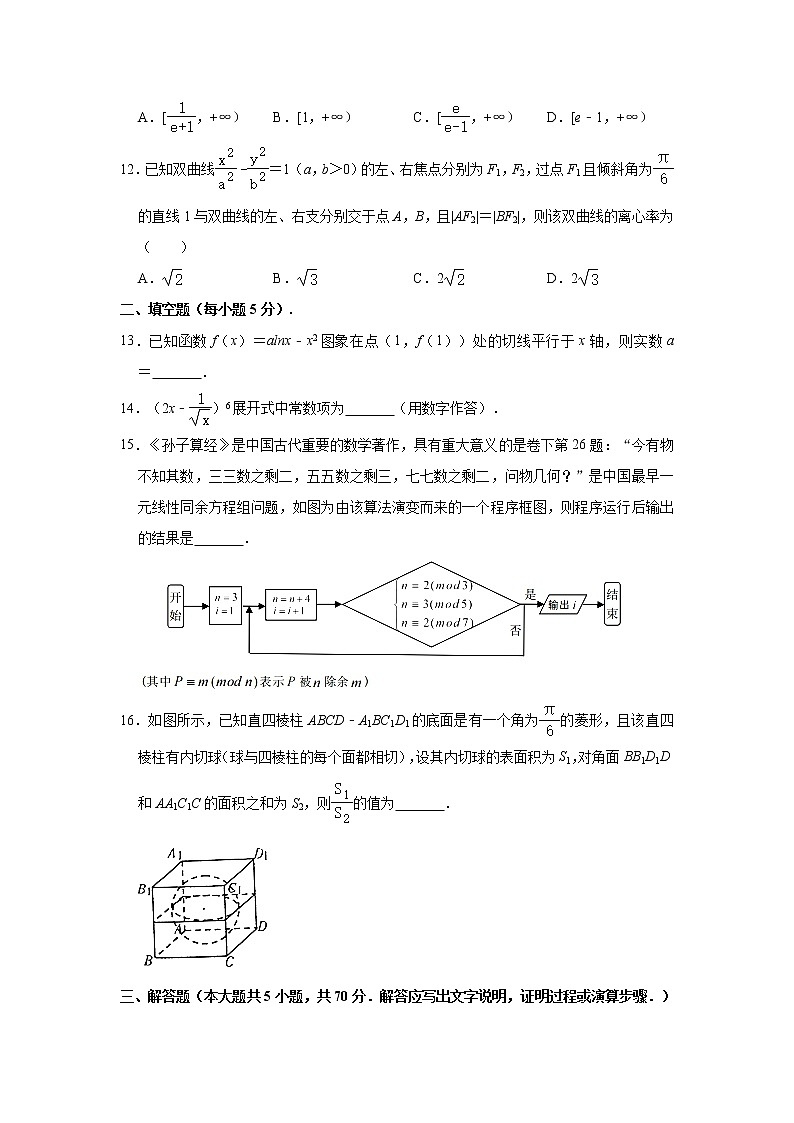
12.已知双曲线=1(a,b>0)的左、右焦点分别为F1,F2,过点F1且倾斜角为的直线1与双曲线的左、右支分别交于点A,B,且|AF2|=|BF2|,则该双曲线的离心率为( )
A. B. C.2 D.2
二、填空题(每小题5分).
13.已知函数f(x)=alnx﹣x2图象在点(1,f(1))处的切线平行于x轴,则实数a= .
14.(2x﹣)6展开式中常数项为 (用数字作答).
15.《孙子算经》是中国古代重要的数学著作,具有重大意义的是卷下第26题:“今有物不知其数,三三数之剩二,五五数之剩三,七七数之剩二,问物几何?”是中国最早一元线性同余方程组问题,如图为由该算法演变而来的一个程序框图,则程序运行后输出的结果是 .
16.如图所示,已知直四棱柱ABCD﹣A1BC1D1的底面是有一个角为的菱形,且该直四棱柱有内切球(球与四棱柱的每个面都相切),设其内切球的表面积为S1,对角面BB1D1D和AA1C1C的面积之和为S2,则的值为 .
三、解答题(本大题共5小题,共70分.解答应写出文字说明,证明过程或演算步骤.)
17.在△ABC中,角A,B,C的对边分别为a,b,c,已知cosA=2sin(C﹣)cosB.
(Ⅰ)求角B的大小;
(Ⅱ)若△ABC的周长为3,且a,b,c成等比数列,求b.
18.如图所示,在四棱锥P﹣ABCD中,PD⊥底面ABCD,四边形ABCD为矩形,CD=2,PD=AD=,E为DC的中点.
(Ⅰ)求证:AE⊥平面PBD;
(Ⅱ)求二面角C﹣PB﹣E的余弦值.
19.已知椭圆C:=1(a>b>0)的左、右焦点分别为F1,F2,M为椭圆C上位于x轴上方一点,线段MF1与圆x2+y2=1相切于该线段的中点,且△MF1F2的面积为2.
(Ⅰ)求椭圆C的方程;
(Ⅱ)过点F2的直线l与椭圆C交于A,B两点,且∠AMB=90°,求直线l的方程.
20.已知函数f(x)=ex+ax(a∈R).
(Ⅰ)讨论f(x)在(0,+∞)上的单调性;
(Ⅱ)若对任意x∈(0,+∞),xex+ax2+(x﹣ln|a|)2≥0恒成立,求a的取值范围.
21.2020年12月16日至18日,中央经济工作会议在北京召开,会议确定,2021年要抓好八个重点任务,其中第五点就是:保障粮食安全,关键在于落实藏粮于地、藏粮于技战略.要加强种质资源保护和利用,加强种子库建设.要尊重科学、严格监管,有序推进生物育种产业化应用.某“种子银行”对某种珍稀名贵植物种子采取“活态保存”方法进行保存,即对种子实行定期更换和种植.通过以往的相关数据表明,该植物种子的出芽率为p(0<p<1),每颗种子是否发芽相互独立.现任取该植物种子2n﹣1颗进行种植,若种子的出芽数X超过半数,则可认为种植成功(n≥2).
(Ⅰ)当n=3,p=时,求种植成功的概率及X的数学期望;
(Ⅱ)现拟加种两颗该植物种子,试分析能否提高种植成功率?
请考生在第22-23题中任选一题作答,如果多做,则按所做的第一题计分.[选修4-4:坐标系与参数方程](本小题满分10分)
22.在极坐标系Ox中,射线l的极坐标方程为θ=(ρ≥0),曲线C的极坐标方程为ρ2﹣4ρsinθ=r2﹣4(r>0),且射线l与曲线C有异于点O的两个交点P,Q.
(Ⅰ)求r的取值范围;
(Ⅱ)求+的取值范围.
[选修4-5:不等式选讲](本小题满分0分)
23.已知函数f(x)=|x+2|﹣|ax﹣2|(a∈R).
(Ⅰ)当a=2时,解不等式f(x)≥1;
(Ⅱ)当x∈[﹣2,2]时,求证:f(x)+f(﹣x)≤0.
参考答案
一、选择题(每小题5分).
1.已知集合M={x|x2﹣5x﹣6<0},N={x|lnx>0},则M∩N=( )
A.{x|0<x<1} B.{x|1<x<6} C.{x|1<x<3} D.{x|2<x<3}
解:∵集合M={x|x2﹣5x﹣6<0}={x|﹣1<x<6},
N={x|lnx>0}={x|x>1},
∴M∩N={x|1<x<6}.
故选:B.
2.已知复数z=,则|z|=( )
A.0 B. C.2 D.﹣2
解:∵=
|z|=
故选:B.
3.已知等差数列{an}的前n项和为Sn,且满足a3=7,S10=20,则a8=( )
A.﹣5 B.﹣3 C.3 D.5
解:设等差数列{an}的公差为d,
由题意得,
解得a1=11,d=﹣2,
故a8=11+7×(﹣2)=﹣3.
故选:B.
4.若实数x,y满足,则z=x﹣2y的最小值为( )
A.﹣6 B.﹣1 C.2 D.6
解:作出不等式组对应的平面区域如图:
由z=x﹣2y得y=x﹣z,
平移直线y=x﹣z,由图象知当直线经过点C时,直线截距最大,此时z最小,
由得,即C(﹣2,2),
此时z=﹣2﹣2×2=﹣6,
故选:A.
5.将函数f(x)=cosx图象上所有点的横坐标都缩短到原来的,再向左平移个单位,得到函数g(x)的图象,则g(x)是( )
A.周期为4π的奇函数 B.周期为4π的偶函数
C.周期为π的奇函数 D.周期为π的偶函数
解:将函数f(x)=cosx图象上所有点的横坐标都缩短到原来的,可得y=cos2x的图象,
再向左平移个单位,得到函数g(x)=cos(2x+)=﹣sin2x的图象,
故g(x)是周期为π的奇函数,
故选:C.
6.恩格尔系数(Engel'sCoefficien)是食品支出总额占个人消费支出总额的比重.居民可支配收入是居民可用于最终消费支出和储蓄的总和,即居民可用于自由支配的收入.如图为我国2013年至2019年全国恩格尔系数和居民人均可支配收入的折线图.
给出三个结论:
①恩格尔系数与居民人均可支配收入之间存在负相关关系;
②一个国家的恩格尔系数越小,说明这个国家越富裕;
③一个家庭收入越少,则家庭收入中用来购买食品的支出所占的比重就越小.
其中正确的是( )
A.① B.② C.①② D.②③
解:由折线图可知,恩格尔系数在逐年下降,
居民人均可支配收入在逐年增加,
故两者之间存在负相关关系,恩格尔系数越小,
居民人均可支配收入越多,经济越富裕,故选项①②正确.
故选:C.
7.如图所示,四边形ABCD是边长为2的菱形,E是边BC上靠近C的三等分点,F为CD的中点,则=( )
A.2 B. C. D.﹣2
解:∵=+,==,
∴=()•()===﹣.
故选:C.
8.已知抛物线E:y2=2px(p>0),斜率为1的直线l过抛物线E的焦点,若抛物线E上有且只有三点到直线l的距离为,则p=( )
A.4 B.2 C.1 D.
解:设l:y=x﹣,设l1:y=x+m与抛物线E相切,
由,可得x2+2(m﹣p)x+m2=0,
△=4(m﹣p)2﹣4m2=0,解得p=2m,且m>0,
平行线l1与l的距离为:d===,
所以p=2,
故选:B.
9.古希腊毕达哥拉斯学派认为数是万物的本源,因此极为重视数的理论研究,他们常把数描绘成沙滩上的沙粒或小石子,并将它们排列成各种形状进行研究.形数就是指平面上各种规则点阵所对应的点数,是毕哥拉斯学派最早研究的重要内容之一.如图是三角形数和四边形数的前四个数,若三角形数组成数列{an},四边形数组成数列{bn},记cn=,则数列{cn}的前10项和为( )
A. B. C. D.
解:由题意可得,,,
所以,
设数列{cn}的前n项和为Sn,
所以,
所以.
故选:D.
10.如图所示,在棱长为2的正方体ABCD﹣A1B1C1D1中,点E,F,G,H,I,J分别是棱A1B1,A1D1,DD1,CD,BC,BB1的中点,现在截面EFGHIJ内随机取一点M,则此点满足|AM|+|MC1|≤4的概率为( )
A. B. C. D.
解:连接AC1交平面EFGHIJ于O,则O为AC1和GJ的交点,
由正方体的性质可得AC1⊥平面EFGHIJ,∴AC1⊥OM,
设|OM|=x,∵AO=OC1=,
∴=,即x≤1,
∴满足|AM|+|MC1|≤4的点M的轨迹所围成的面积为π,
又截面EFGHIJ的面积为,
故所求概率P=.
故选:D.
11.若不等式xm(ex+x)≤emx+mxm(x﹣lnx)恒成立,则实数m的取值范围是( )
A.[,+∞) B.[1,+∞) C.[,+∞) D.[e﹣1,+∞)
解:不等式xm(ex+x)≤emx+mxm(x﹣lnx)恒成立⇔ex+x≤+m(x﹣lnx)=em(x﹣lnx)+m(x﹣lnx),
令f(x)=ex+x,则原不等式等价于f(x)≤f(m(x﹣lnx))恒成立.
∵f(x)=ex+x在(0,+∞)上单调递增,
∴x≤m(x﹣lnx),
令g(x)=x﹣lnx,则g′(x)=1﹣=,
可得:x=1时函数g(x)取得极小值,即最小值.
∴g(x)≥g(1)=1>0.
∴x≤m(x﹣lnx)⇔m≥,
令h(x)=,x∈(0,+∞).
∴h′(x)=.
h′(e)=0,x∈(0,e)时,h′(x)>0,∴h(x)在(0,e)上单调递增;
x∈(e,+∞)时,h′(x)<0,∴h(x)在(e,+∞)上单调递减.
∴h(x)max=h(e)=.
∴实数m的取值范围是[,+∞).
故选:C.
12.已知双曲线=1(a,b>0)的左、右焦点分别为F1,F2,过点F1且倾斜角为的直线1与双曲线的左、右支分别交于点A,B,且|AF2|=|BF2|,则该双曲线的离心率为( )
A. B. C.2 D.2
解:过F2作F2N⊥AB于点N,设|AF2|=|BF2|=m,
因为直线l的倾斜角为,
所以在直角三角形F1F2N中,|NF2|=c,|NF1|=c,
由双曲线的定义可得|BF1|﹣|BF2|=2a,所以|BF1|=2a+m,
同理可得|AF1|=m﹣2a,所以|AB|=|BF1|﹣|AF1|=4a,
即|AN|=2a,
所以|AF1|=c﹣2a,因此m=c,
在直角三角形ANF2中,|AF2|2=|NF2|2+|AN|2,
所以(c)2=4a2+c2,所以c=a,
则e==.
故选:A.
二、填空题(本大题共4小题,每小题5分,共20分.)
13.已知函数f(x)=alnx﹣x2图象在点(1,f(1))处的切线平行于x轴,则实数a= 2 .
解:由f(x)=alnx﹣x2,得f′(x)=,
∴f′(1)=a﹣2,
由题意,a﹣2=0,得a=2.
故答案为:2.
14.(2x﹣)6展开式中常数项为 60 (用数字作答).
解:(2x﹣)6展开式的通项为=
令得r=4
故展开式中的常数项.
故答案为60
15.《孙子算经》是中国古代重要的数学著作,具有重大意义的是卷下第26题:“今有物不知其数,三三数之剩二,五五数之剩三,七七数之剩二,问物几何?”是中国最早一元线性同余方程组问题,如图为由该算法演变而来的一个程序框图,则程序运行后输出的结果是 6 .
解:模拟程序的运行,可得
n=3,i=1
n=7,i=2
不满足判断框条件,n=11,i=3
不满足判断框条件,n=15,i=4
不满足判断框条件,n=19,i=5
不满足判断框条件,n=23,i=6
满足判断框条件,故输出的i的值为6.
故答案为:6.
16.如图所示,已知直四棱柱ABCD﹣A1BC1D1的底面是有一个角为的菱形,且该直四棱柱有内切球(球与四棱柱的每个面都相切),设其内切球的表面积为S1,对角面BB1D1D和AA1C1C的面积之和为S2,则的值为 .
解:设∠ABC=α,AB=a,内切球的半径为R,则2R=asinα,∴R=,
四棱柱的高为:asinα,∴S1=4πR2,由题意可得AC+BD=2a(sin+cos),
∴S2=2a(sin+cos)•asinα=a2(sin+cos)sinα,
∴=====.
故答案为:.
三、解答题(本大题共5小题,共70分.解答应写出文字说明,证明过程或演算步骤.)
17.在△ABC中,角A,B,C的对边分别为a,b,c,已知cosA=2sin(C﹣)cosB.
(Ⅰ)求角B的大小;
(Ⅱ)若△ABC的周长为3,且a,b,c成等比数列,求b.
解:(Ⅰ)因为cosA=2sin(C﹣)cosB,
所以cosA=2(sinCcos﹣cosCsinB)cosB,可得cosA=sinCcosB﹣cosCcosB,
因为cosA=﹣cos(B+C)=sinBsinC﹣cosBcosC,
所以sinBsinC﹣cosBcosC=sinCcosB﹣cosBcosC,可得sinBsinC=sinCcosB,
因为sinC≠0,
所以sinB=cosB,可得tanB=,
因为B∈(0,π),
所以B=.
(Ⅱ)由余弦定理可得b2=a2+c2﹣2accos,即b2=a2+c2﹣ac,
因为a,b,c成等比数列,
所以b2=ac,
所以ac=a2+c2﹣ac,可得a=c,
所以△ABC是等边三角形,
又a+b+c=3,
所以b=1.
18.如图所示,在四棱锥P﹣ABCD中,PD⊥底面ABCD,四边形ABCD为矩形,CD=2,PD=AD=,E为DC的中点.
(Ⅰ)求证:AE⊥平面PBD;
(Ⅱ)求二面角C﹣PB﹣E的余弦值.
【解答】(Ⅰ)证明:因为PD⊥平面ABCD,AE⊂平面ABCD,
所以PD⊥AE,
因为四边形ABCD为矩形,CD=2,AD=,E为DC的中点.
所以tan∠EAD===,tan∠CDB==,
于是∠DAE=∠CDB,因为∠DAE+∠DEA=90°,所以∠EDF+∠DEF=90°,所以AE⊥BD,
因为PD∩BD=D,PD、BD⊂平面PBD,所以AE⊥平面PBD;
(Ⅱ)解:建立如图所示的空间直角坐标系,
=(,2,﹣),=(0,1,﹣),=(0,2,﹣),
设平面PBE和平面PBC的法向量分别为=(x,y,z),=(u,v,w),
,令y=,=(﹣1,,1),
,令v=1,=(0,1,),
因为二面角C﹣PB﹣E为锐角,
所以二面角C﹣PB﹣E的余弦值为==.
19.已知椭圆C:=1(a>b>0)的左、右焦点分别为F1,F2,M为椭圆C上位于x轴上方一点,线段MF1与圆x2+y2=1相切于该线段的中点,且△MF1F2的面积为2.
(Ⅰ)求椭圆C的方程;
(Ⅱ)过点F2的直线l与椭圆C交于A,B两点,且∠AMB=90°,求直线l的方程.
解:(Ⅰ)设线段MF1的中点为N,则|ON|=1,
又ON是△MF1F2的中位线,
所以|MF2|=2,MF1⊥MF2,
由椭圆的定义知|MF1|=2a﹣2,
因为△MF1F2面积为S=(2a﹣2)×2=2a﹣2=2,解得a=2,
因为|F1F2|===2,解得c=2,
所以b==,
所以椭圆C的方程为+=1.
(Ⅱ)当直线l的斜率为0时,此时∠AMB≠90°,不合题意,
当直线l的斜率不为0时,设直线l的方程为x=my+,A(x1,y1),B(x2,y2),
联立,得(2+m2)y2+2my﹣2=0,
所以y1+y2=﹣,y1y2=,
由(Ⅰ)知M(0,),
因为∠AMB=90°,
所以MA⊥MB,
所以x1x2+(y1﹣)(y2﹣)=0,
所以(1+m2)y1y2+(m﹣1)(y1+y2)+4=0,
所以﹣+4=0,
所以m2﹣2m﹣3=0,
解得m=﹣1或m=3,
当m=﹣1时,直线l过点M,不符合题意,
所以直线l的方程为x﹣3y﹣=0.
20.已知函数f(x)=ex+ax(a∈R).
(Ⅰ)讨论f(x)在(0,+∞)上的单调性;
(Ⅱ)若对任意x∈(0,+∞),xex+ax2+(x﹣ln|a|)2≥0恒成立,求a的取值范围.
解:(I)f′(x)=ex+a,当a≥﹣1时,∵x>0,∴ex>1,∴f′(x)=ex+a>0,∴f(x)在(0,+∞)上的单调递增.
当a<﹣1时,ln(﹣a)>0,∴x>ln(﹣a)时,f′(x)>0;x<ln(﹣a)时,f′(x)<0.
∴f(x)在(0,ln(﹣a))上的单调递减,在(ln(﹣a),+∞)上的单调递增.
综上可得:当a≥﹣1时,f(x)在(0,+∞)上的单调递增.
当a<﹣1时,f(x)在(0,ln(﹣a))上的单调递减,在(ln(﹣a),+∞)上的单调递增.
(II)当a≥﹣1且a≠0时,由(I)可知:f(x)在(0,+∞)上的单调递增,∴f(x)>f(0)=1.
∴x>0时,xex+ax2+(x﹣ln|a|)2≥0恒成立⇔ex+ax+x+﹣2ln|a|≥0恒成立.
a<﹣1时,令u(x)=ex+ax+x+﹣2ln|a|,
∵y=x+﹣2ln|a|,在(0,ln(﹣a))上的单调递减,在(ln(﹣a),+∞)上的单调递增.
由(I)可知:f(x)=ex+ax,在(0,ln(﹣a))上的单调递减,在(ln(﹣a),+∞)上的单调递增.
∴u(x)在(0,ln(﹣a))上的单调递减,在(ln(﹣a),+∞)上的单调递增.
∴u(x)min=u(ln(﹣a))=eln(﹣a)+aln(﹣a)+ln(﹣a)+﹣2ln(﹣a)=eln(﹣a)+aln(﹣a)=﹣a+aln(﹣a)=a(ln(﹣a)﹣1),
∴a(ln(﹣a)﹣1)≥0,解得:﹣e≤a<﹣1.
综上可得:a的取值范围是[﹣e,0)∪(0,+∞).
21.2020年12月16日至18日,中央经济工作会议在北京召开,会议确定,2021年要抓好八个重点任务,其中第五点就是:保障粮食安全,关键在于落实藏粮于地、藏粮于技战略.要加强种质资源保护和利用,加强种子库建设.要尊重科学、严格监管,有序推进生物育种产业化应用.某“种子银行”对某种珍稀名贵植物种子采取“活态保存”方法进行保存,即对种子实行定期更换和种植.通过以往的相关数据表明,该植物种子的出芽率为p(0<p<1),每颗种子是否发芽相互独立.现任取该植物种子2n﹣1颗进行种植,若种子的出芽数X超过半数,则可认为种植成功(n≥2).
(Ⅰ)当n=3,p=时,求种植成功的概率及X的数学期望;
(Ⅱ)现拟加种两颗该植物种子,试分析能否提高种植成功率?
解:(Ⅰ)由题意可知,X服从二项分布B(5,),故P(X=k)=(k=3,4,5),
故种植成功的概率为=,
E(X)==;
(Ⅱ)设种植2n﹣1颗种子时,种植成功的概率为P1,拟加种两颗该植物种子时,种植成功的概率为P2,
当种植2n+1颗种子时,考虑前2n﹣1颗种子出芽数,
为了种植成功,前2n﹣1颗种子中至少要有n﹣1颗种子出芽,
①前2n﹣1颗种子中恰有n﹣1颗出芽,它的概率为,
此时后两颗种子必须都要出芽,
所以这种情况下种植成功的概率为•p2;
②前2n﹣1颗种子恰有n颗出芽,它的概率为,
此时后两颗种子至少有一颗出芽即可,
所以这种情况下种植成功的概率为•[1﹣(1﹣p)2];
③前2n﹣1颗种子至少有n+1颗出芽,它的概率为,此时种植一定成功.
所以P2=•p2+•[1﹣(1﹣p)2]+,
故P2﹣P1=•p2+•[1﹣(1﹣p)2],
=,
因为,
所以=,
所以当时,P2<P1,种植成功率会降低;
当时,P2=P1,种植成功率不变;
当时,P2>P1,种植成功率会提高.
请考生在第22-23题中任选一题作答,如果多做,则按所做的第一题计分.[选修4-4:坐标系与参数方程](本小题满分10分)
22.在极坐标系Ox中,射线l的极坐标方程为θ=(ρ≥0),曲线C的极坐标方程为ρ2﹣4ρsinθ=r2﹣4(r>0),且射线l与曲线C有异于点O的两个交点P,Q.
(Ⅰ)求r的取值范围;
(Ⅱ)求+的取值范围.
解:(Ⅰ)射线l的极坐标方程为θ=(ρ≥0),转换为直角坐标方程为(x≥0).
曲线C的极坐标方程为ρ2﹣4ρsinθ=r2﹣4(r>0),根据,转换为直角坐标方程为x2+(y﹣2)2=r2.
且射线l与曲线C有异于点O的两个交点P,Q.
所以圆心(0,2)到直线y=的距离d=,
所以1<r<2.
(Ⅱ)把为θ=,代入ρ2﹣4ρsinθ=r2﹣4,
得到,
所以,,
由于r∈(1,2),
所以4﹣r2∈(0,3)
所以+=.
[选修4-5:不等式选讲](本小题满分0分)
23.已知函数f(x)=|x+2|﹣|ax﹣2|(a∈R).
(Ⅰ)当a=2时,解不等式f(x)≥1;
(Ⅱ)当x∈[﹣2,2]时,求证:f(x)+f(﹣x)≤0.
解:(Ⅰ)当a=2时,f(x)≥1即|x+2|﹣|2x﹣2|≥1等价为或或,
解得x∈∅或≤x<1或1≤x≤3,
所以原不等式的解集为[,3];
(Ⅱ)证明:当x∈[﹣2,2]时,f(x)=|x+2|﹣|ax﹣2|=x+2﹣|ax﹣2|,
f(﹣x)=2﹣x﹣|ax+2|,f(x)+f(﹣x)=4﹣(|ax﹣2|+|ax+2|),
因为|ax﹣2|+|ax+2|≥|ax﹣2﹣(ax+2)|=4,当(ax﹣2)(ax+2)≤0时,取得等号,
所以4﹣(|ax﹣2|+|ax+2|)≤0,
即f(x)+f(﹣x)≤0.
2023年江西省鹰潭市高考数学二模试卷(理科)-普通用卷: 这是一份2023年江西省鹰潭市高考数学二模试卷(理科)-普通用卷,共21页。试卷主要包含了单选题,填空题,解答题等内容,欢迎下载使用。
2021年江西省九江市高考数学三模试卷(理科)(含解析): 这是一份2021年江西省九江市高考数学三模试卷(理科)(含解析),共22页。试卷主要包含了单选题,填空题,解答题等内容,欢迎下载使用。
2022年江西省萍乡市高考数学二模试卷(理科)(含答案解析): 这是一份2022年江西省萍乡市高考数学二模试卷(理科)(含答案解析),共18页。












