

- 专题13.15 《轴对称》全章复习与巩固(专项练习)(培优篇)-2021-2022学年八年级数学上册基础知识专项讲练(人教版) 试卷 7 次下载
- 专题13.16 课题-最短路径(将军饮马问题)(知识讲解)-2021-2022学年八年级数学上册基础知识专项讲练(人教版) 其他 7 次下载
- 专题13.18 课题-最短路径(将军饮马问题)(专项练习)(提高篇)-2021-2022学年八年级数学上册基础知识专项讲练(人教版) 试卷 9 次下载
- 专题13.19 课题-最短路径(将军饮马问题)(专项练习)(培优篇)-2021-2022学年八年级数学上册基础知识专项讲练(人教版) 试卷 7 次下载
- 专题13.20《轴对称》中考真题专练(基础篇)(专项练习)-2021-2022学年八年级数学上册基础知识专项讲练(人教版) 试卷 5 次下载
专题13.17 课题-最短路径(将军饮马问题)(专项练习)(基础篇)-2021-2022学年八年级数学上册基础知识专项讲练(人教版)
展开专题13.17 课题-最短路径(将军饮马问题)
(专项练习)(基础篇)
一、单选题
1.如图,直线L是一条河,P,Q是两个村庄.欲在L上的某处修建一个水泵站,向P,Q两地供水,现有如下四种铺设方案,图中实线表示铺设的管道,则所需管道最短的是( )
A. B. C.D.
2.如图,在△ABC中,AB=3,AC=4,BC=5,EF是BC的垂直平分线,P是直线EF上的任意一点,则PA+PB的最小值是( )
A.3 B.4 C.5 D.6
3.如图,A是直线l外一点,点B,E,D,C在直线l上,且,D为垂足,如果量得,,,,则点A到直线l的距离为( )
A.11 cm B.7 cm C.6 cm D.5 cm
4.如图,在中,,,的面积为12,于点D,直线EF垂直平分BC交AB于点E,交BC于点F,P是线段EF上的一个动点,则的周长的最小值是( )
A.6 B.7 C.10 D.12
5.如图,在△ABC中,AB⊥AC,AB=3,BC=5,AC=4,EF垂直平分BC,点P为直线EF上的任意一点,则△ABP周长的最小值是( )
A.12 B.6 C.7 D.8
6.如图,等腰三角形ABC的底边BC长为3,面积是18,腰AC的垂直平分线EF分别交AC,AB边于E,F点.若点D为BC边的中点,点M为线段EF上一动点,则△CDM周长的最小值为( )
A.6 B.8 C.10 D.13.5
7.如图,分别是线段的垂直平分线,,一只小蚂蚁从点M出发爬到边上任意一点E,再爬到边上任意一点F,然后爬回M点,则小蚂蚁爬行的最短路径为( )
A. B. C. D.
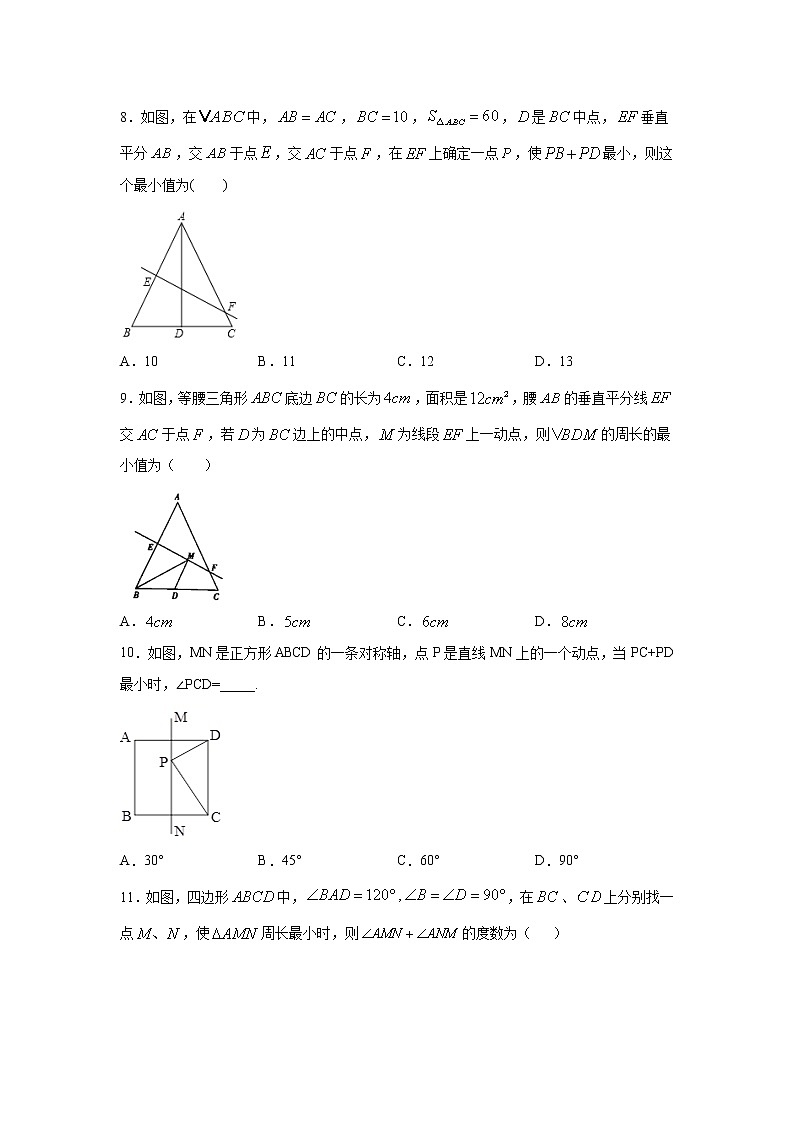
8.如图,在中,,,,是中点,垂直平分,交于点,交于点,在上确定一点,使最小,则这个最小值为( )
A.10 B.11 C.12 D.13
9.如图,等腰三角形底边的长为,面积是,腰的垂直平分线交于点,若为边上的中点,为线段上一动点,则的周长的最小值为( )
A. B. C. D.
10.如图,MN是正方形ABCD的一条对称轴,点P是直线MN上的一个动点,当PC+PD最小时,∠PCD=_____.
A.30° B.45° C.60° D.90°
11.如图,四边形中,,在、上分别找一点,使周长最小时,则的度数为( )
A. B. C. D.
12.如图已知,为内一定点,上有一点,上有一点,当的周长取最小值时,的度数是( )
A. B. C. D.
二、填空题
13.如图,要从村庄P修一条连接公路的最短的小道,应选择沿线段________修建,理由是________.
14.如图,在中,,,,垂直平分,点为直线上的任意一点,则周长的最小值是__________.
15.如图,Rt△ABC中,∠C=90°,AC=3,BC=4,EF垂直平分AB,点P为直线EF上一动点,则△APC周长的最小值为_____.
16.如图,在中,,,,是的垂直平分线,是直线上的任意一点,则的最小值是________.
17.如图,在中BC=5,垂直平分BC,点P为直线EF上一动点,则周长的最小值是________.
18.如图,等腰三角形ABC的面积为90,底边BC=12,腰AC的垂直平分线EF交AC,AB于点E,F,若D为BC边中点,M为线段EF上一动点,则的周长最小值为________
19.如图,在中,,,的垂直平分线交于点,交于点,在直线上存在一点,使、、三点构成的的周长最小,则的周长最小值为______.
20.如图,在等边中,是的中点,是的中点,是上任意一点.如果,,那么的最小值是 .
21.如图,AC⊥BC,AC=6,BC=8,AB=10,则点B到AC的距离为_____.
22.如图,在锐角中,,边上有一定点分别是和边上的动点,当的周长最小时,的度数是_________.
23.如图,在中.,若,,,将折叠,使得点C恰好落在AB边上的点E处,折痕为AD,点P为AD上一动点,则的周长最小值为___.
三、解答题
24.如图,小明在A处放牛,要到河边(直线l)给牛喝水,喝完水把牛赶回家中B处.
(1)要使路程最短,应该在河边哪处给牛喝水,请在直线l上画出喝水处点P的位置;
(2)在直线l上任取一点Q(点Q不与点P重合),连接,试说明.
25.如图,BA、BC是两条公路,在两条公路夹角内部的点P处有一油库,若在两公路上分别建个加油站,并使运油的油罐车从油库出发先到一加油站,再到另一加油站,最后回到油库的路程最短,则加油站应如何选址?
26.作图题:(不写作法,但必须保留作图痕迹)
(1)如图,已知点M.N和∠AOB,求作一点P,使P到点M.N的距离相等,且到∠AOB的两边的距离相等.
(2)要在河边修建一个水泵站,分别向张村.李庄送水(如图). 修在河边l什么地方,可使所用水管最短?试在图中确定水泵站的位置.
27.如图,点A、B在直线l同侧,请你在直线l上画出一点P,使得的值最小,画出图形并证明.
28.如图,准备在一条公路旁修建一个仓储基地,分别给A、B两个超市配货,那么这个基地建在什么位置,能使它到两个超市的距离之和最小?(保留作图痕迹及简要说明)
参考答案
1.A
【分析】
利用对称的性质,通过等线段代换,将所求路线长转化为两定点之间的距离.
【详解】
作点P关于直线L的对称点P′,连接QP′交直线L于M.
根据两点之间,线段最短,可知选项D铺设的管道,则所需管道最短.
故选:A.
【点拨】本题考查了最短路径的数学问题.这类问题的解答依据是“两点之间,线段最短”.由于所给的条件的不同,解决方法和策略上又有所差别.
2.B
【分析】
根据题意知点B关于直线EF的对称点为点C,故当点P-为EF和AC的交点时,AP+BP值最小为AC的长为4.
【详解】
解:如图:
∵EF垂直平分BC,
∴B、C关于EF对称,
∴当AC交EF于P时,AP+BP的值最小,最小值等于AC的长为4,
故选:B.
【点拨】本题考查轴对称——最短路线问题的应用.解决此题的关键是能根据轴对称的性质和两点之间线段最短找出P点的位置.
3.D
【分析】
根据点到直线的垂线段的长度是点到直线的距离可知AD的长度是点A到直线l的距离,从而得解.
【详解】
∵AD=5cm,∴点A到直线l的距离是5cm.
故选D.
【点拨】本题主要考查了点到直线的距离的定义,熟记定义是解题的关键.
4.B
【分析】
根据等腰三角形三线合一的性质可知为底边上的高线,根据面积关系即可求得的长,根据垂直平分线的性质可知点和点关于直线EF对称,所以当与重合时,的值最小,根据和的长度即可求得周长的最小值.
【详解】
如图
∵的面积为12,
∴,,
解得,,
∵直线EF垂直平分BC交AB于点E,
∴点和点关于直线EF对称,
∴当与重合时,的值最小,最小值等于的长,
∴周长的最小值是,
故选:B.
【点拨】本题考查了等腰三角形的性质、垂直平分线的性质、轴对称最短路线问题的应用、三角形的面积等,解题的关键是准确找出点的位置.
5.C
【分析】
根据题意知点B关于直线EF的对称点为点C,故当点P与点D重合时,AP+BP的最小值,即可得到△ABP周长的最小值.
【详解】
解:∵EF垂直平分BC,
∴B、C关于EF对称,
设AC交EF于D,
∴当P和D重合时,及A、P、C三点共线时
AP+BP的值最小,最小值等于AD+BD=AD+CD=AC的长,
∴△ABP周长的最小值是AB+AC=3+4=7.
故选:C.
【点拨】本题考查了勾股定理,轴对称-最短路线问题的应用,解此题的关键是找出P的位置.凡是涉及最短距离的问题,一般要考虑线段的性质定理,结合轴对称变换来解决,多数情况要作点关于某直线的对称点.
6.D
【分析】
连接AD,由于△ABC是等腰三角形,点D是BC边的中点,故AD⊥BC,再根据三角形的面积公式求出AD的长,再根据EF是线段AC的垂直平分线可知,点C关于直线EF的对称点为点A,故AD的长为CM+MD的最小值,由此即可得出结论.
【详解】
解:连接AD,
∵△ABC是等腰三角形,点D是BC边的中点,
∴AD⊥BC,
∴S△ABC=BC•AD=×3×AD=18,解得AD=12,
∵EF是线段AC的垂直平分线,
∴点C关于直线EF的对称点为点A,
∴AD的长为CM+MD的最小值,
∴△CDM的周长最短=(CM+MD)+CD=AD+BC=12+×3=12+1.5=13.5.
故选D.
【点拨】本题考查的是轴对称-最短路线问题,熟知等腰三角形三线合一的性质是解答此题的关键.
7.B
【分析】
由题意可知与的交点为E,与的交点为F,根据垂直平分线的性质计算即可;
【详解】
由题意可知与的交点为E,与的交点为F.
∵分别是线段的垂直平分线,
∴,
∴小蚂蚁爬行的最短路径为.
【点拨】本题主要考查了最短路线问题和垂直平分线的性质,准确计算是解题的关键.
8.C
【分析】
根据三角形的面积公式得到AD=12,由EF垂直平分AB,得到点A,B关于直线EF对称,于是得到AD的长为PB+PD的最小值,即可得到结论.
【详解】
∵AB=AC,BC=10,S△ABC=60,AD⊥BC于点D,
∴S△ABC==60,
∴AD=12,
设AD与EF的交点为P,
∵EF垂直平分AB,
∴点A,B关于直线EF对称,
∴PA=PB,
此时AD的长为PB+PD的最小值,
即PB+PD的最小值为12,
故选:C.
【点拨】本题考查了轴对称-最短路线问题,线段的垂直平分线的性质,等腰三角形的性质的运用,凡是涉及最短距离的问题,一般要考虑线段的性质定理,结合轴对称变换来解决,多数情况要作点关于某直线的对称点.
9.D
【分析】
连接AD,由于△ABC是等腰三角形,点D是BC边的中点,故AD⊥BC,再根据三角形的面积公式求出AD的长,再根据EF是线段AB的垂直平分线可知,点B关于直线EF的对称点为点A,故AD的长为BM+MD的最小值,由此即可得出结论.
【详解】
连接AD,
∵△ABC是等腰三角形,点D是BC边的中点,
∴AD⊥BC,
∴S△ABC=BC•AD=×4×AD=12,解得AD=6cm,
∵EF是线段AB的垂直平分线,
∴点B关于直线EF的对称点为点A,
∴AD的长为BM+MD的最小值,
∴△BDM的周长最短=(BM+MD)+BD=AD+BC=6+×4=6+=8cm.
【点拨】本题考查轴对称-最短路线问题、线段垂直平分线的性质和等腰三角形的性质,解题的关键是掌握轴对称-最短路线问题、线段垂直平分线的性质和等腰三角形的性质.
10.B
【分析】
根据当PC+PD最小时,作出D点关于MN的对称点,正好是A点,连接AC即可得出∠PCD的度数.
【详解】
∵当PC+PD最小时,作出D点关于MN的对称点,正好是A点,
连接AC,AC为正方形对角线,根据正方形的性质得出∠PCD=45°,
∴∠PCD=45°.
故选B.
【点拨】此题考查轴对称求最短路线问题,根据已知得出D点关于MN的对称点,正好是A点是解题关键.
11.C
【分析】
根据要使△AMN的周长最小,即利用点的对称,让三角形的三边在同一直线上,作出A关于BC和CD的对称点A′,A″,即可得出∠AA′M+∠A″=60°,进而得出∠AMN+∠ANM=2(∠AA′M+∠A″)即可得出答案.
【详解】
作A关于BC和CD的对称点A′,A″,连接A′A″,交BC于M,交CD于N,则A′A″即为△AMN的周长最小值。,
∵∠DAB=120°,
∴∠AA′M+∠A″=180°−120°=60°,
∵∠MA′A=∠MAA′,∠NAD=∠A″,
且∠MA′A+∠MAA′=∠AMN,∠NAD+∠A″=∠ANM,
∴∠AMN+∠ANM=∠MA′A+∠MAA′+∠NAD+∠A″=2(∠AA′M+∠A″)=2×60°=120°,
故选:C.
【点拨】此题考查轴对称-最短路线问题,解题关键在于作辅助线.
12.B
【分析】
设点P关于OM、ON对称点分别为P′、P″,当点A、B在P′P″上时,△PAB周长为PA+AB+BP=P′P″,此时周长最小.根据轴对称的性质,可求出∠APB的度数.
【详解】
分别作点P关于OM、ON的对称点P′、P″,连接OP′、OP″、P′P″,P′P″交OM、ON于点A. B,
连接PA、PB,此时△PAB周长的最小值等于P′P″.
由轴对称性质可得,OP′=OP″=OP,∠P′OA=∠POA,∠P″OB=∠POB,
∴∠P′OP″=2∠MON=2×40°=80°,
∴∠OP′P″=∠OP''P′=(180°−80°)÷2=50°
又∵∠BPO=∠OP″B=50°,∠APO=∠AP′O=50°,
∴∠APB=∠APO+∠BPO=100°.
故选B.
【点拨】此题考查轴对称-最短路线问题,解题关键在于作辅助线.
13.PC 垂线段最短
【分析】
根据垂线段的性质:垂线段最短,进行判断即可.
【详解】
解:∵从直线外一点到这条直线上各点所连线段中,垂线段最短,
∴过点P作PC⊥l于点C,这样做的理由是垂线段最短.
故答案为:PC,垂线段最短.
【点拨】本题主要考查了垂线段的性质,从直线外一点引一条直线的垂线,这点和垂足之间的线段叫做垂线段.
14.10
【分析】
如图,根据题意知点关于直线的对称点为点,故当点与点重合时,的最小值等于的长,根据,的长度即可得到周长的最小值.
【详解】
∵垂直平分,
∴点与点关于对称,
如图,设与相交于点,
∴当和重合时,的值最小,最小值等于的长,
∵,,
∴的周长的最小值是,
故答案为:10.
【点拨】本题考查了轴对称-最短路线问题的应用、垂直平分线的性质,解答此题的关键是准确找出点的位置.
15.7
【分析】
△APC周长,因为AC=3,所以求出AP+CP的最小值即可求出△APC周长的最小值,根据题意知点关于直线EF的对称点为点B,故当点P与点E重合时,AP+CP的值最小,即可得到结论.
【详解】
∵直线EF垂直平分AB,
∴A,B关于直线EF对称,
设直线EF交BC于E,
∴当P和E重合时,AP+CP的值最小,最小值等于BC的长,
∴△APC周长的最小值,
故答案为:7.
【点拨】本题考查了轴对称-最短路线问题的应用、垂直平分线的性质、三角形周长,解答本题的关键是准确找出P的位置.
16.4
【分析】
根据题意知点B关于直线EF的对称点为点C,故当点P为AC与EF的交点时,AP+BP的最小值,依据AC的长度即可得到结
【详解】
解:∵EF是BC中垂线,
∴点B关于直线EF的对称点为C,
当点P为AC与EF的交点时,PA+PB取得最小值,且PC=PB
∴最小值为PA+PC=AC=4,
故答案为:4.
【点拨】本题考查垂直平分线的性质、最短距离问题等知识,解题的关键是学会利用轴对称,根据两点之间线段最短解决最短问题.
17.7
【分析】
根据题意知点B关于直线EF的对称点为点C,故当点P与点D重合时,AP+BP的最小值,求出AC长度即可得到结论.
【详解】
解:∵EF垂直平分BC,
∴B、C关于EF对称,
连接AC交EF于D,
∴当P和D重合时,AP+BP的值最小,最小值等于AC的长,
∴△ABP周长的最小值是4+3=7.
故答案为:7.
【点拨】本题考查了轴对称-最短路线问题的应用,解此题的关键是找出P的位置.
18.21
【分析】
连接,,由于是等腰三角形,点是边的中点,故,再根据三角形的面积公式求出的长,再根据是线段的垂直平分线可知,点关于直线的对称点为点,,推出,故的长为的最小值,由此即可得出结论.
【详解】
解:连接,.
是等腰三角形,点是边的中点,
,
,解得,
是线段的垂直平分线,
点关于直线的对称点为点,,
,
的长为的最小值,
的周长最短,
故答案是:21.
【点拨】本题考查的是轴对称最短路线问题,熟知等腰三角形三线合一的性质是解答此题的关键.
19.18
【分析】
连接PA.因为△PBC的周长=BC+PB+PC,BC=8cm,推出PB+PC的值最小时,△PBC的周长最小.由题意PA=PB,推出PB+PC=PA+PC≥AC=10cm,由此即可解决问题.
【详解】
解:如图,连接PA.
∵△PBC的周长=BC+PB+PC,BC=8cm,
∴PB+PC的值最小时,△PBC的周长最小,
∵MN垂直平分线段AB,
∴PA=PB,
∴PB+PC=PA+PC≥AC=10cm,
∴PB+PC的最小值为10cm,
∴△PBC的周长的最小值为18cm.
故答案为18cm.
【点拨】本题考查轴对称最短问题,等腰三角形的性质,线段的垂直平分线的性质等知识,解题的关键是学会用转化的思想思考问题,属于中考常考题型.
20.
【分析】
从题型可知为”将军饮马”的题型,连接CE,CE即为所求最小值.
【详解】
∵△ABC是等边三角形,
∴B点关于AD的对称点就是C点,
连接CE交AD于点H,此时HE+HB的值最小.
∴CH=BH,
∴HE+HB=CE,
根据等边三角形的性质,可知三条高的长度都相等,
∴CE=AD=.
故答案为: .
【点拨】本题考查三角形中动点最值问题,关键在于寻找对称点即可求出最值.
21.8
【解析】
试题解析:AC⊥BC,AC=6,BC=8,AB=10,则点B到AC的距离为8
22.80°
【分析】
根据对称的性质,易求得∠C+∠EPF=180°,由 ∠ACB=50°,易求得∠D+∠G=50°,继而求得答案;
【详解】
∵ PD⊥AC,PG⊥BC,
∴∠PEC=∠PFC=90°,
∴ ∠C+∠EPF=180°,
∵∠C=50°,
∵∠D+∠G+∠EPF=180°,
∴ ∠D+∠G=50°,
由对称可知:∠G=∠GPN,∠D=∠DPM, L
∴∠GPN+∠DPM=50°,
∴∠MPN=130°-50°=80°,
故答案为:80°.
【点拨】此题考查了最短路径问题以及线段垂直平分线的性质,关键是注意掌握数形结合思想的应用.
23.20.
【分析】
根据由沿AD对称,得到,进而表示出,最后求周长即可.
【详解】
由沿AD对称得到,
则E与C关于直线AD对称,
,
∴,
如图,连接,
由题意得,
∴,
当P在BC边上,即D点时取得最小值12,
∴周长为,最小值为.
故答案为:20.
【点拨】本题考查了三角形折叠问题,正确读懂题意是解本题的关键.
24.(1)见解析;(2)见解析
【分析】
(1)要使PA+PB最短,根据同一平面内线段最短,可知要作点A关于直线l的对称点A′,连接A′B交直线l于P;
(2)在直线l上任取另一点Q,连接PA、QA、QB.根据轴对称的性质得到PA=PA′,QA=QA′.根据三角形的三边关系即可得到结论.
【详解】
解:(1)如图,点P即为所求.
(2)如图,在直线l上任取一点Q,连接.
∵点A与关于直线l对称,点P,Q在直线l上,
∴.
∵,
∴,即,
∴.
【点拨】本题考查了轴对称,以及三角形的三边关系,正确确定如何使线段的和最小是关键.
25.见解析
【分析】
利用关于直线对称点的性质得出 P 点关于AB的对称点 P ',以及 P 点关于 CB 的对称点 P ",根据两点直接线段最短,连接 P ' P "即可得出.
【详解】
解:如图所示:C、D点即为所求.
【点拨】此题主要考查了应用作图与设计,两点之间线段最短,利用关于直线对称点的性质得出是解题关键.
26.(1)见解析;(2)见解析.
【分析】
(1)根据题意可知只要作出∠AOB的角平分线、线段MN的垂直平分线,然后找到这两条线的交点即为所求;
(2)作B点关于小河的对称点B′,连接B′A与小河的交点C,点C就是所求.
【详解】
解:(1)如图所示:作出∠AOB的角平分线、线段MN的垂直平分线,这两条线的交点即为所求P点
.
(2)作点B关于河岸的对称点B′,连接B′A,交河岸于点C,CA+CB=AB′的长度之和最短,则修在河边l的点C处,可使所用水管最短.
【点拨】本题考查作图—复杂作图,角平分线的性质,线段垂直平分线的性质,轴对称与最短路线问题,熟练掌握相关性质是解题关键.
27.见解析
【分析】
作点A关于直线l的对称点A′,连接A′B交直线l于P,连接PA.则点P即为所求的点.
【详解】
解:如图,则点P即为所求的点.
证明:∵点A关于l的对称点A',
根据对称性可知,PA=PA',
因此,求AP+BP最小就相当于求BP+PA'最小,
显然当A'、P、B在一条直线上时A'P+PB最小,因此连接A'B,与直线l的交点,就是要求的点P.
【点拨】本题考查了轴对称-最短路线问题,熟练掌握轴对称的性质的应用是解题的关键.
28.见解析.
【分析】
作点B关于公路的对称点,连接交公路于点C,根据两点之间线段最短即可得出点C即是所求的点.
【详解】
解:如图,作点B关于公路的对称点,连接,交公路于点C,则这个基地建在C处,才能使它到这两个超市距离之和最小。
【点拨】本题考查了最短路径问题,要求熟练掌握中垂线的性质,能够利用两点之间线段最短求解一些简单的实际问题.
初中数学人教版八年级下册17.1 勾股定理课时作业: 这是一份初中数学人教版八年级下册<a href="/sx/tb_c10261_t7/?tag_id=28" target="_blank">17.1 勾股定理课时作业</a>,共37页。试卷主要包含了单选题,填空题,解答题等内容,欢迎下载使用。
初中数学人教版八年级下册17.1 勾股定理课时训练: 这是一份初中数学人教版八年级下册<a href="/sx/tb_c10261_t7/?tag_id=28" target="_blank">17.1 勾股定理课时训练</a>,共36页。试卷主要包含了单选题,填空题,解答题等内容,欢迎下载使用。
专题22.27 二次函数“将军饮马”问题(巩固篇)(专项练习)-2022-2023学年九年级数学上册基础知识专项讲练(人教版): 这是一份专题22.27 二次函数“将军饮马”问题(巩固篇)(专项练习)-2022-2023学年九年级数学上册基础知识专项讲练(人教版),共37页。试卷主要包含了单选题,填空题,解答题等内容,欢迎下载使用。












