

2020-2021学年北京市密云区九年级(上)期末数学试卷
展开2020-2021学年北京市密云区九年级(上)期末数学试卷
一、选择题(本题共24分,每小题3分)下面各题均有四个选项,其中只有一个选项是符合题意的.
1.(3分)抛物线的顶点坐标是
A. B. C. D.
2.(3分)如图,直线,直线被,,所截得的两条线段分别为、,直线被,,所截得的两条线段分别为、.若,,,则的长为
A.0.6 B.1.2 C.2.4 D.3.6
3.(3分)已知点,是反比例函数图象上的两点,则
A. B. C. D.
4.(3分)将的各边长都缩小为原来的,则锐角的正弦值
A.不变 B.缩小为原来的
C.扩大为原来的2倍 D.缩小为原来的
5.(3分)如图,二次函数的图象经过点,和,则下列结论错误的是
A.二次函数图象的对称轴是直线
B.方程的两根是,
C.当时,函数值随自变量的增大而减小
D.函数的最小值是
6.(3分)如图,是的直径,、是上的两点,,则的度数为
A. B. C. D.
7.(3分)如图,在平面直角坐标系中有两点和,以原点为位似中心作,与的相似比为2,其中点与点对应,点与点对应,且在轴左侧,则点的坐标为
A. B. C. D.
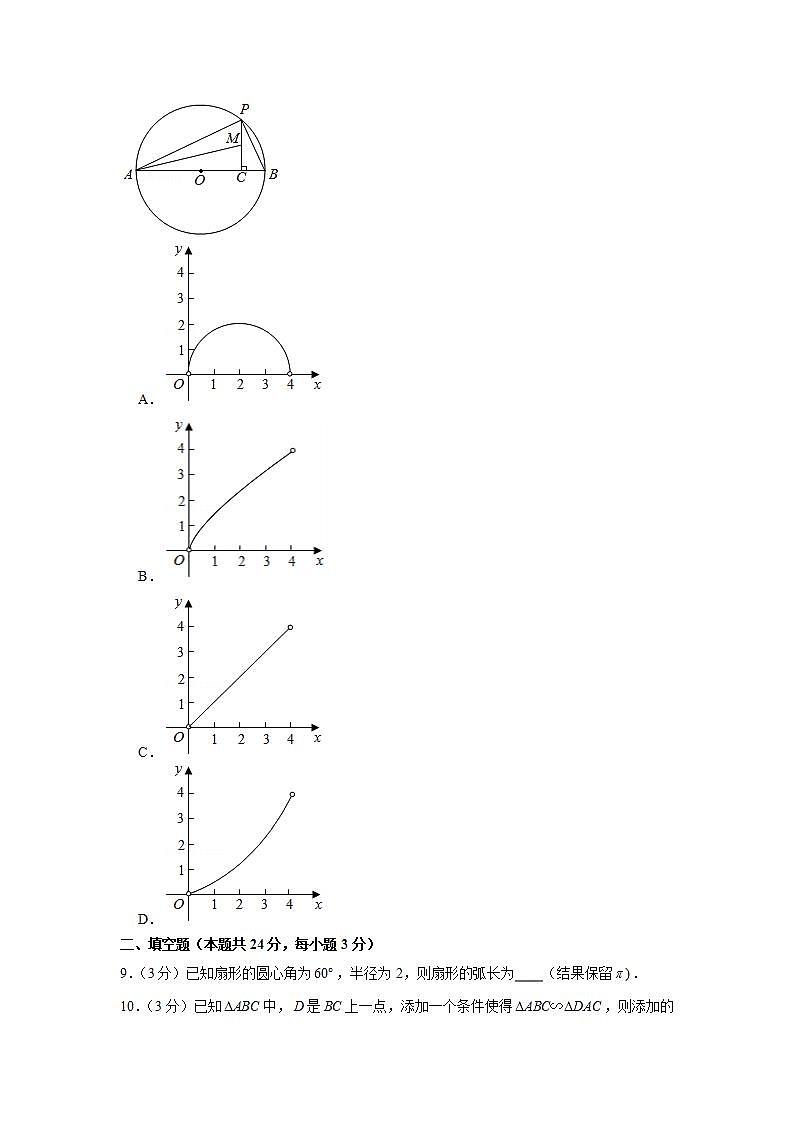
8.(3分)如图,是的直径,,是圆周上一动点(点与点、点不重合),,垂足为,点是的中点.设长为,长为,则表示与之间函数关系的图象大致为
A.
B.
C.
D.
二、填空题(本题共24分,每小题3分)
9.(3分)已知扇形的圆心角为,半径为2,则扇形的弧长为 (结果保留.
10.(3分)已知中,是上一点,添加一个条件使得,则添加的条件可以是 .
11.(3分)已知点,、,是反比例函数图象上的两点,其中,则 .
12.(3分)如图,中,是中点,与交于点,则与的面积比为 .
13.(3分)二次函数的最小值是 .
14.(3分)如图,、、是上三点,,垂足为.已知,,则长为 .
15.(3分)如图是某商场自动扶梯的示意图.自动扶梯的倾斜角为在自动扶梯下方地面处测得扶梯顶端的仰角为,、之间的距离为,则自动扶梯的垂直高度 .(结果保留根号)
16.(3分)《九章算术》是我国古代数学名著,也是古代东方数学的代表作之一.书中记载了一个问题:“今有勾五步,股十二步,问勾中容圆径几何?”译文:“如图,今有直角三角形,勾(短直角边)长为5步,股(长直角边)长为12步,问该直角三角形能容纳的圆(内切圆)的直径是多少步?”
根据题意,该直角三角形内切圆的直径为 步.
三、解答题(本题共52分,其中17-21每题5分,22题6分,23-25题每题7分)
17.(5分)计算:.
18.(5分)已知抛物线经过两点,.
(1)求该抛物线的表达式;
(2)在平面直角坐标系内画出抛物线的示意图;
(3)若直线经过,两点,结合图象直接写出不等式的解集.
19.(5分)如图,,,点在上,,,,.
(1)求证:;
(2)求的度数.
20.(5分)如图,四边形中,,,,,求的长.
21.(5分)已知双曲线与直线交于和.
(1)求、值;
(2)将直线平移得到,且,与双曲线围成的封闭区域内(不含边界)恰有3个整点(把横纵坐标均为整数的点称为整点)结合图象,直接写出的取值范围.
22.(6分)如图,是的直径,、是圆上两点,,过点作的垂线分别交,延长线于点,.
(1)求证:是的切线;
(2)若,,求的半径.
23.(7分)已知抛物线与轴交于点,将点向右平移4个单位得到点,点也在抛物线上.
(1)抛物线的对称轴是直线 ;
(2)用含的代数式表示;
(3)已知点,,抛物线与线段恰有一个公共点,求的取值范围.
24.(7分)如图,矩形中,,平分交于点,将线段绕点逆时针旋转得到线段,连接,与交于点.
(1)①补全图形;
②设的度数为,直接写出的度数(用含的代数式表示).
(2)连接,用等式表示线段,,之间的数量关系,并证明.
25.(7分)对于平面直角坐标系中的图形,,给出如下定义:是图形上的任意一点,是图形上任意一点,如果,两点间距离有最小值,则称这个最小值为图形,的“最小距离”,记作.
已知的半径为1.
(1)如图,,则(点, ,(点, .
(2)已知、是上两点,且的度数为.
①若轴且在轴上方,直线,求的值;
②若点坐标为,,直接写出(点,的取值范围.
2020-2021学年北京市密云区九年级(上)期末数学试卷
参考答案与试题解析
一、选择题(本题共24分,每小题3分)下面各题均有四个选项,其中只有一个选项是符合题意的.
1.(3分)抛物线的顶点坐标是
A. B. C. D.
【解答】解:是抛物线的顶点式,
抛物线的顶点坐标为.
故选:.
2.(3分)如图,直线,直线被,,所截得的两条线段分别为、,直线被,,所截得的两条线段分别为、.若,,,则的长为
A.0.6 B.1.2 C.2.4 D.3.6
【解答】解:直线,
,
,,,
,
,
故选:.
3.(3分)已知点,是反比例函数图象上的两点,则
A. B. C. D.
【解答】解:中,
此函数图象的两个分支分别位于第一、三象限,且在每一象限内随的增大而减小,
,
,
故选:.
4.(3分)将的各边长都缩小为原来的,则锐角的正弦值
A.不变 B.缩小为原来的
C.扩大为原来的2倍 D.缩小为原来的
【解答】解:设,,,
则,
由题意得,缩小后三边长是,,,
,
锐角的正弦值不变,
故选:.
5.(3分)如图,二次函数的图象经过点,和,则下列结论错误的是
A.二次函数图象的对称轴是直线
B.方程的两根是,
C.当时,函数值随自变量的增大而减小
D.函数的最小值是
【解答】.由点、的坐标知,二次函数图象的对称轴是直线,故正确,不符合题意;
.由函数图象知,与轴交点坐标为、,故方程的两根是,,故正确,不符合题意;
.抛物线的对称轴为直线,从图象看,当时,函数值随自变量的增大而减小,故正确,不符合题意;
.设抛物线的表达式为,当时,,解得,
故抛物线的表达式为,当时,函数的最小值为,故错误,符合题意,
故选:.
6.(3分)如图,是的直径,、是上的两点,,则的度数为
A. B. C. D.
【解答】解:,
(圆周角定理),
是的直径,
,
,
故选:.
7.(3分)如图,在平面直角坐标系中有两点和,以原点为位似中心作,与的相似比为2,其中点与点对应,点与点对应,且在轴左侧,则点的坐标为
A. B. C. D.
【解答】解:点和,以原点为位似中心作,与的相似比为2,点与点对应,点与点对应,且在轴左侧,
点的坐标为.
故选:.
8.(3分)如图,是的直径,,是圆周上一动点(点与点、点不重合),,垂足为,点是的中点.设长为,长为,则表示与之间函数关系的图象大致为
A.
B.
C.
D.
【解答】解:是直径,则,
则,
而,
,
则,
则,即,
点是的中点,则,
则,
即是开口向上的抛物线,
为1时,值大于1,
故选:.
二、填空题(本题共24分,每小题3分)
9.(3分)已知扇形的圆心角为,半径为2,则扇形的弧长为 (结果保留.
【解答】解:依题意,,,
扇形的弧长.
故答案为.
10.(3分)已知中,是上一点,添加一个条件使得,则添加的条件可以是 .
【解答】解:添加,
又,
,
故答案为:(答案不唯一).
11.(3分)已知点,、,是反比例函数图象上的两点,其中,则 0 .
【解答】解:点,、,是反比例函数图象上的两点,
,,
,
,
故答案为0.
12.(3分)如图,中,是中点,与交于点,则与的面积比为 .
【解答】解:平行四边形,
,,
,,
,
,
为中点,
,
,
,
故答案为:.
13.(3分)二次函数的最小值是 .
【解答】解:二次函数可化为,
最小值是.
14.(3分)如图,、、是上三点,,垂足为.已知,,则长为 .
【解答】解:连接,如图所示:
,
,
,,
,
,
,
故答案为:.
15.(3分)如图是某商场自动扶梯的示意图.自动扶梯的倾斜角为在自动扶梯下方地面处测得扶梯顶端的仰角为,、之间的距离为,则自动扶梯的垂直高度 .(结果保留根号)
【解答】解:,,,
,
,
,
在中,
,
故答案为:.
16.(3分)《九章算术》是我国古代数学名著,也是古代东方数学的代表作之一.书中记载了一个问题:“今有勾五步,股十二步,问勾中容圆径几何?”译文:“如图,今有直角三角形,勾(短直角边)长为5步,股(长直角边)长为12步,问该直角三角形能容纳的圆(内切圆)的直径是多少步?”
根据题意,该直角三角形内切圆的直径为 4 步.
【解答】解:如图,,,,为的内切圆,分别与三边切于、、,
连接、,如图,设的半径为,
、与相切,
,,
四边形为矩形,
而,
矩形为正方形,
,
,,
,,
,,
,
,解得,
的直径为4.
故答案为4.
三、解答题(本题共52分,其中17-21每题5分,22题6分,23-25题每题7分)
17.(5分)计算:.
【解答】解:原式
.
18.(5分)已知抛物线经过两点,.
(1)求该抛物线的表达式;
(2)在平面直角坐标系内画出抛物线的示意图;
(3)若直线经过,两点,结合图象直接写出不等式的解集.
【解答】解:(1)抛物线经过两点,.
,
解得,
抛物线的表达式为.
(2)画出函数图象如图;
(3)由图象可知,不等式的解集为.
19.(5分)如图,,,点在上,,,,.
(1)求证:;
(2)求的度数.
【解答】(1)证明:,,点在上,
.
,,,,
,.
.
;
(2)由(1)知,,则.
,
.
.
20.(5分)如图,四边形中,,,,,求的长.
【解答】解:,,,
,
,
,,
.
21.(5分)已知双曲线与直线交于和.
(1)求、值;
(2)将直线平移得到,且,与双曲线围成的封闭区域内(不含边界)恰有3个整点(把横纵坐标均为整数的点称为整点)结合图象,直接写出的取值范围.
【解答】解:(1)点在双曲线上,
.
双曲线的表达式为
点在双曲线上,
;
(2)由函数图象可知,
若直线在直线的下方时,;
若直线在直线的上方时,;
综上,的取值范围是:或.
22.(6分)如图,是的直径,、是圆上两点,,过点作的垂线分别交,延长线于点,.
(1)求证:是的切线;
(2)若,,求的半径.
【解答】(1)证明:连接,,
,
,
,
,
,
,
,
,
,
,
是的切线;
(2)解:在中,,
,
,
设,,则,
,
,
,
,,
,
,
,
,
.
23.(7分)已知抛物线与轴交于点,将点向右平移4个单位得到点,点也在抛物线上.
(1)抛物线的对称轴是直线 2 ;
(2)用含的代数式表示;
(3)已知点,,抛物线与线段恰有一个公共点,求的取值范围.
【解答】解:(1)抛物线与轴交于点,
,
将点向右平移4个单位得到点,
;
与关于对称轴对称,
抛物线对称轴直线,
故答案为2;
(2)抛物线对称轴直线,
,
;
(3)解:由(2)可知,抛物线的表达式为,
令,解得:,,
抛物线经过和
设点,在抛物线上,则,.
故此点在上方,
①当时,若使抛物线与线段恰有一个公共点,需满足点与点重合(如图或点在点下方(如图,即,
解得:,即,
②当时,,故此点在点下方,此时抛物线与线段恰有一个公共点(如图,
综上所述:的取值范围是:或.
24.(7分)如图,矩形中,,平分交于点,将线段绕点逆时针旋转得到线段,连接,与交于点.
(1)①补全图形;
②设的度数为,直接写出的度数(用含的代数式表示).
(2)连接,用等式表示线段,,之间的数量关系,并证明.
【解答】解:(1)①补全图形如下:
②将线段绕点逆时针旋转得到线段,
,,
,
,
,
.
(2).
证明:延长,交于点,
四边形是矩形,
,
平分,
,
,
,
,
,
,
,
,
,
,
,
,
.
25.(7分)对于平面直角坐标系中的图形,,给出如下定义:是图形上的任意一点,是图形上任意一点,如果,两点间距离有最小值,则称这个最小值为图形,的“最小距离”,记作.
已知的半径为1.
(1)如图,,则(点, 1 ,(点, .
(2)已知、是上两点,且的度数为.
①若轴且在轴上方,直线,求的值;
②若点坐标为,,直接写出(点,的取值范围.
【解答】解:(1),
,
的半径为1,
(点,,(点,,
故答案为:1,4.
(2)①如图1中,不妨假设点在点的右侧,连接,.
设直线交轴于,交轴于,
则,,,
,
,
的度数为,
,
,
是等边三角形,
,
轴,
,
,
,
过点作于.
,,
,
.
②如图2中,连接.
,,
,
当点或点在时,的值最小,最小值.
如图3中,当交于时,的值最大,最大值,
.
声明:试题解析著作权属菁优网所有,未经书面同意,不得复制发布
日期:2021/12/6 11:47:12;用户:初中数学1;邮箱:jse032@xyh.com;学号:39024122
北京市密云区2023~2024学年上学期九年级期末数学试卷: 这是一份北京市密云区2023~2024学年上学期九年级期末数学试卷,共7页。
2021-2022学年北京市密云区七年级(上)期末数学试卷(含答案解析): 这是一份2021-2022学年北京市密云区七年级(上)期末数学试卷(含答案解析),共13页。试卷主要包含了12×105B,【答案】B,【答案】A,【答案】D,【答案】>等内容,欢迎下载使用。
2021-2022学年北京市密云区九年级(上)期末数学试卷(学生版+解析版): 这是一份2021-2022学年北京市密云区九年级(上)期末数学试卷(学生版+解析版),共27页。













