高中数学人教版新课标A必修51.2 应用举例教课内容课件ppt

这是一份高中数学人教版新课标A必修51.2 应用举例教课内容课件ppt，共11页。PPT课件主要包含了解根据正弦定理得，解由余弦定理得，实际问题，解应用题的基本思路等内容，欢迎下载使用。

例1、设A、B两点在河的两岸，要测量两点之间的距离。
测量者在A的同测，在所在的河岸边选定一点C，测出AC的距离是55cm，∠BAC＝51， ∠ACB＝75，求A、B两点间的距离（精确到0.1m）
分析：已知两角一边，可以用正弦定理解三角形
答：A,B两点间的距离为65.7米。
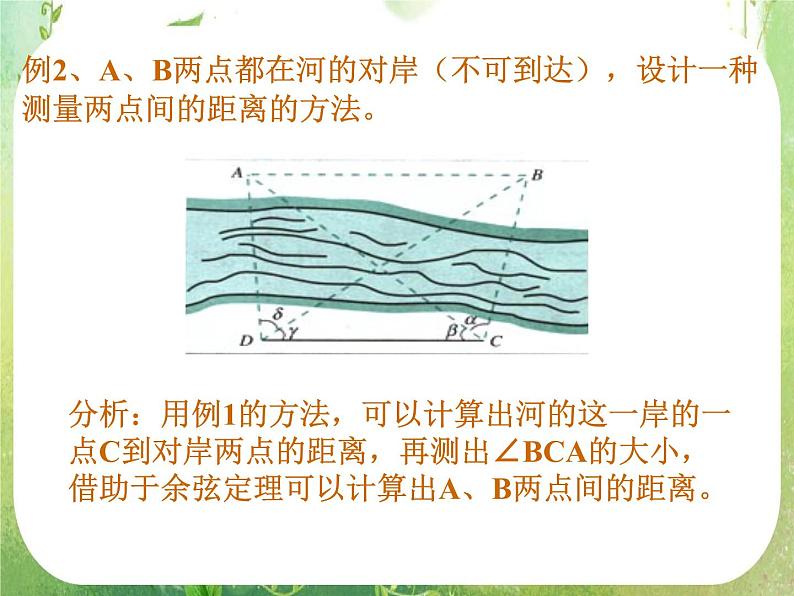
例2、A、B两点都在河的对岸（不可到达），设计一种测量两点间的距离的方法。
分析：用例1的方法，可以计算出河的这一岸的一点C到对岸两点的距离，再测出∠BCA的大小，借助于余弦定理可以计算出A、B两点间的距离。
解：测量者可以在河岸边选定两点C、D，测得CD=a,并且在C、D两点分别测得∠BCA=α, ∠ACD=β, ∠CDB=γ, ∠BDA=δ.在⊿ADC和⊿BDC中，应用正弦定理得
计算出AC和BC后，再在⊿ABC中，应用余弦定理计算出AB两点间的距离
练习1、一艘船以32.2n mile / hr的速度向正北航行。在A处看灯塔S在船的北偏东20的方向，30min后航行到B处，在B处看灯塔在船的北偏东65的方向，已知距离此灯塔6.5n mile 以外的海区为航行安全区域，这艘船可以继续沿正北方向航行吗？
（1）什么是最大仰角？
在△ABC中已知什么，要求什么？
已知△ABC中AB＝1.95m，AC＝1.40m， 夹角∠CAB＝66°20′，求BC．
答：顶杆BC约长1.89m。
已知⊿ABC中，三个内角A,B,C的对边分别是a,b,c,若⊿ABC的面积为S,且2S=(a+b)²－c²,求tanC的值。