初中第7章 有理数7.4 有理数的乘除法背景图ppt课件

这是一份初中第7章 有理数7.4 有理数的乘除法背景图ppt课件，共60页。PPT课件主要包含了例1计算，异号两数相乘，把绝对值相乘，同号两数相乘，计算下面各式，－600，－756，对于乘法成立吗，加法的交换律，加法的结合律等内容，欢迎下载使用。

观察数轴，点A表示－3，点B表示什么?
甲水库的水位每天升高 2.5 厘米，乙水库的水位每天下降 2.5 厘米，6 天后甲、乙水库水位的总变化量各是多少？
如果用正号表示水位上升，用负号表示水位下降那么4天后甲水库的水位变化量为：2.5 ＋ 2.5＋ 2.5＋ 2.5 ＝ 2.5×4 ＝10（厘米）乙水库的水位变化量为：　（－2.5）＋（－2.5）＋（－2.5）＋（－2.5）＝（－2.5）×4 ＝－10（厘米）
如图,一辆汽车沿公路m行驶，它现在的位置是在m上的点Ｏ．
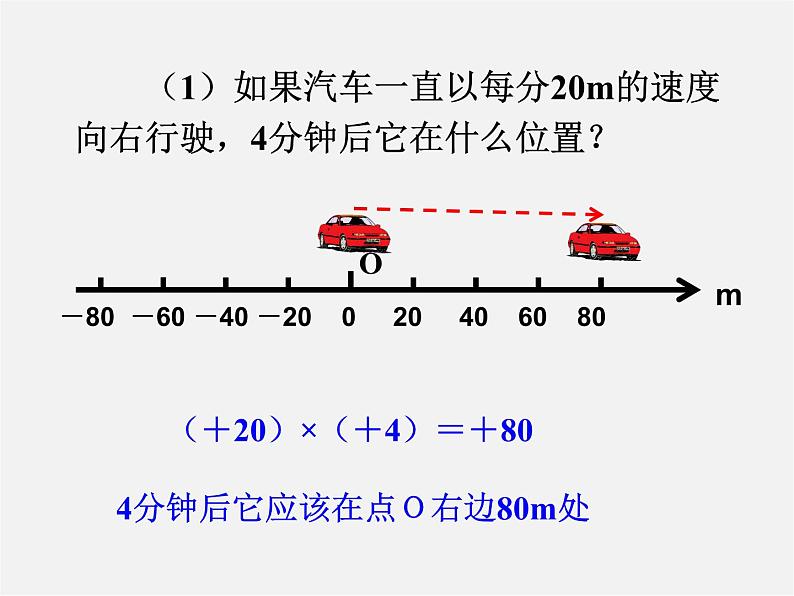
（1）如果汽车一直以每分20m的速度向右行驶，4分钟后它在什么位置？
（＋20）×（＋4）＝＋80
4分钟后它应该在点Ｏ右边80m处
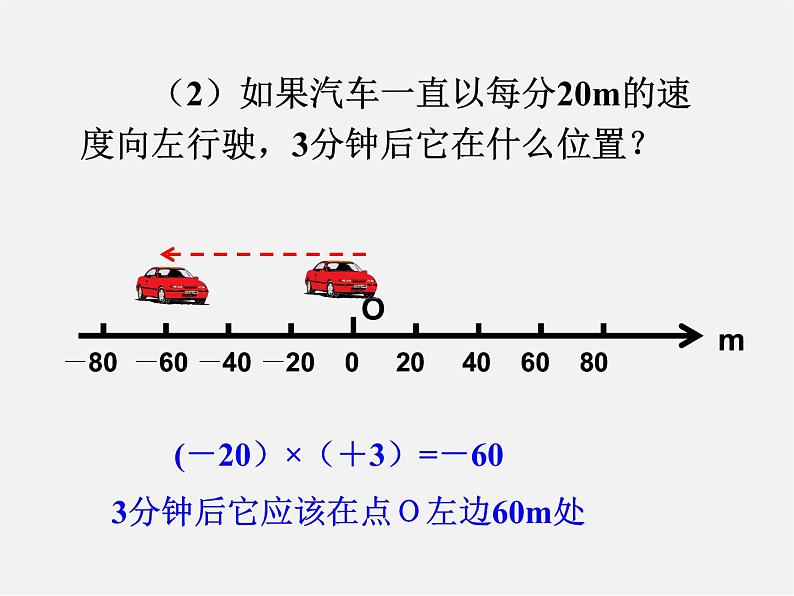
（2）如果汽车一直以每分20m的速度向左行驶，3分钟后它在什么位置？
(－20）×（＋3）=－60
3分钟后它应该在点Ｏ左边60m处
（3）如果汽车一直以每分20cm的速度向右行驶，4分钟前它在什么位置？
(＋20）×（－4）=－80
3分钟前它应该在点Ｏ左边80m处
（4）如果汽车一直以每分20m的速度向左行驶，3分钟前它在什么位置？
(－20）×（－3）=＋60
3分钟前它应该在点Ｏ右边60m处
正数乘正数积为____数负数乘正数积为____数正数乘负数积为____数负数乘负数积为____数
乘积的绝对值等于各乘数绝对值的乘积
（＋20）×（＋4）=＋80（－20）×（＋3）=－60（＋20）×（－4）=－80（－20）×（－3）=＋60
有理数乘法的法则 两数相乘，同号得正，异号得负，并把绝对值相乘． 任何数同0相乘，都得0．
解：（－4）×8 ＝－（4×8） ＝－32
有理数相乘，先确定积的符号，再确定积的绝对值．
（－5）×（－6） ＝＋（5×6） ＝30
乘积是1的两个数互为倒数．
请你举出几个互为倒数的例子；　　数a(a≠0)的倒数是什么？a为什么不能等于0?
　　乘积是１的两个数互为倒数．一个数同+1相乘，得原数，一个数同-1相乘，得原数的相反数． 遇到带分数，一般先化成假分数．
例2：在山地，气温随海拔的升高而降低，大致每升高1km，气温约下降6 ℃．用正负数表示气温的变化量，上升为正，下降为负．某人攀登一座山峰，登高4km后，气温有什么变化？
解：（－6）×4=－24．答：气温下降24℃．
（1）4×5×（－5）×6
（2） 4×3×（－4）×2×（－3）
（3） （－3）×3×7×（－6）×（－2）
（4） （－4）×5×3×（－2）×（－7）×0
（5） 4×6×7×0
几个不是0的数相乘时，负因数的个数是偶数时，积是正数，负因数的个数为奇数时，积是负数． 　几个数相乘，如果其中有因数为0，积等于0．
a + b = b + a（a + b）+ c = a +（b + c）
a×b = b×a（a×b）×c = a×（b×c）
（－4）×（－6）=24，（－6 ） ×（－4） =24， （－4）×（－6）=（－6 ） ×（－5）. [（－2） ×（－4）] ×5=8×5=40（－2） ×[（－4） ×5]=（－2） ×（－20）=40 [（－2） ×（－4）] ×5=（－2） × [（－4） ×5].
乘法的交换律　　有理数的乘法中，两个数相乘，交换因数的位置，积相等．即：ab=ba
乘法的结合律　　有理数的乘法中，三个数相乘，先把前两个数相乘，或者先把后两个数相乘，积相等．即：（ab）c=a（bc）
4 ×[（－5）+（－8）] ＝ 4 ×（－5）+4 ×（－8）（－6）×3＋（－6）×（－4）＝（－6）×[3＋(－4)
观察下面两个等式，是否成立？
乘法的分配律　　有理数的乘法中，一个数同两个数的和相乘，等于把这个数分别同这两个数相乘，再把积相加．即：a（b+c）=ab+ac
例4：分别用两种方法计算下列各式：
（1）解法1： 解法2:
（2）解法1： 解法2:
1．有理数乘法法则：　　两数相乘,同号得正,异号得负,并把绝对值相乘,任何数同0相乘，都得0．2．如何进行两个有理数的运算：　　先确定积的符号，再把绝对值相乘，当有一个因数为零时，积为零．
3．有理数乘法法则：　　乘法的交换律：ab=ba　　乘法的结合律：（ab）c=a（bc）　　乘法的分配律：a（b+c）=ab+ac4．有理数乘法的运算及表示方法5．如何运用运算律来简化运算
　　1．若干个不等于0的有理数相乘，积的符号 （    ）　　　A．由因数的个数决定  　　B．由正因数的个数决定　　C．正因数的个数决定  　 D．由负因数的个数决定　　
　　　3．2009个有理数相乘的积为0，那么（　　 ）　　A．每个因数一定都是零     　 B．每个因数都不为零　　C．至少有一个因数不为零 　 D．至少有一个因数为零　　4．一个数和它的相反数的积是（  　 ）　　A．正数  B．一定不大于0　  C．负数  D．一定不小于0
4．如果ab<0，且a0，b>0　　B．a<0，b>0C．a>0，b<0　　D．a<0，b<05．如果ab>0，则必有（　　）A．a>0，b>0　　B．a<0，b>0C．A，b同号　　D．a<0，b<0
你能很快地说出下列各数的倒数吗?
因为 (－3)×3＝ －9,
所以 (－9)÷3＝ －3.
除以一个正数等于乘以这个正数的倒数.
因为(－3)×(－3)=9,所以 (－9) ÷(－3)=3.
因为3×(－3) ＝－9,所以9÷ (－3) ＝－3.
因为0×(－3)=0,所以 0÷ (－3)=0.
有理数的除法法则 除以一个不等于0的数，等于乘以这个数的倒数.即：
　　两数相除，两数符号相同则结果为正，两数符号不同则结果为负，并把绝对值相除．
0除以任何一个不等于0的数都得0.
有理数除法法则 两数相除，同号得正，异号得负，并把绝对值相除. 0除以任何一个不等于0的数都得0.
　　分数可以理解为分子除以分母．
乘除法混合运算，统一成乘法
无括号，只有乘除，从左向右计算
有理数的加减乘除混合运算 如有括号的先算括号里的，无括号则按照“先乘除，后加减”的顺序进行。
　　1．因为0没有倒数，所以，0不能作除数；　　2．在除法运算中，符号的确定与乘法运算一致；　　3．遇到乘除法混合运算时，应按照从左到右的顺序进行；　　4．遇到求带分数的倒数时，先将带分数化为假分数，再求其倒数．
例9：为提醒广大市民做好防冻御寒工作，下列为某地区一周内最低气温预报。具体气温如下：
(1)　求本周的平均最低气温？
解：〔（－2）+（－5）+（－4） +0 +（－4）　　+（－3）＋（－3）〕÷7 　＝（－21）÷7 　＝－3
例10：今抽查10袋精盐，每袋精盐的标准重量是100克，超出部分记为正，统计成下表：
问：这种10袋盐一共有多重？
解：0.8＋3×（－0.5）＋0＋3×1.3＋2×（－1.2） ＝0.8－1.5＋3.9－2.4 ＝0.8 100×10＋0.8＝1000.8.答：这10袋盐一共重1000.8克.
我们可以用计算器进行复杂的数的计算.
0.8＋3×（－0.5）＋0＋3×1.3＋2×（－1.2）
解：用带符号键 的计算器，
（1）653＋（－450）＋261＋（－123）；（2）（－25）×33＋（－26）×（－46）；（3）18.72÷（－52）－（－1430）÷22；（4）5.6×（－46）÷（－0.25）×3。
1．有理数除法法则　 （1） （2）有理数除法法则：两数相除，同号得正，异号得负，并把绝对值相除. （3）0除以任何一个不等于0的数都得0.2．有理数的加减乘除混合运算： 如有括号的先算括号里的，无括号则按照“先乘除，后加减”的顺序进行.
1.填空题（1）当x= _____时， 没有意义;（2）当x= _____时， 的值为0;（3）当x= _____时， 没有意义.
2. 下列说法正确的是（ ）A．负数没有倒数B．正数的倒数比自身小C．任何有理数都有倒数D．－1的倒数是－13. 下列运算结果不一定为负数的是（ ）A．异号两数相乘B．异号两数相除C．异号两数相加D．奇数个负因数的乘积
m=＋4时，原式=2 004m=－4时，原式=2 012