2022中考数学总复习——整式的乘法 专项复习(共46张PPT)课件PPT

这是一份2022中考数学总复习——整式的乘法 专项复习(共46张PPT)课件PPT，共46页。PPT课件主要包含了ma+b，ma+mb，指数相乘，指数相加，-2b，a+2b，-4x3y2，2a+b²，-a6，-ac等内容，欢迎下载使用。

(a+b)(m+n)=
am+an+bm+bn
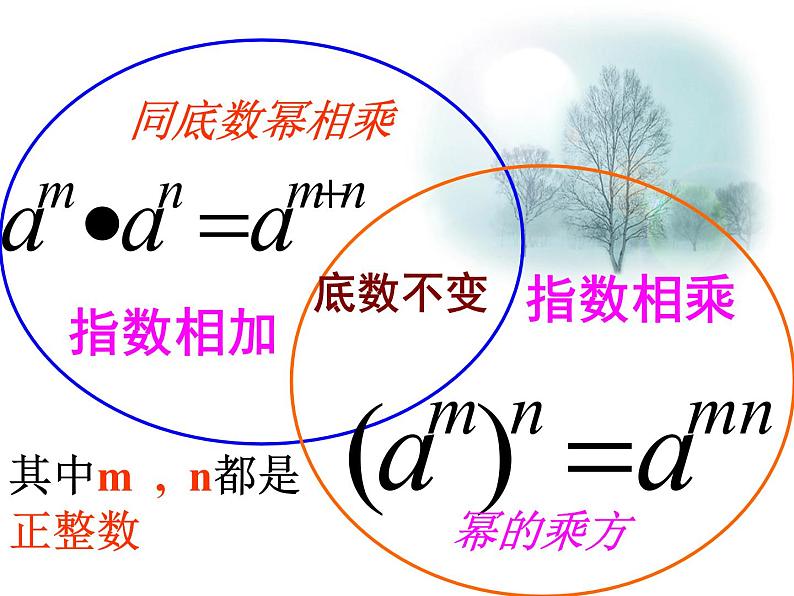
其中m , n都是正整数
下列各式中运算正确的是（ ）
( )
( )
公 式 的 反 向 使 用
(ab)n = an·bn
an·bn = (ab)n
(1) 23×53 ;
(2) (-5)16 × (-2)15
(3) 24 × 44 ×(-0.125)4 ;
= (-5)×[(-5)×(-2)]15
= [2×4×(-0.125)]4
(1) (x5y) ÷ x2 = x5 − 2 ·y(2) (8m2n2) ÷ (2m2n) = (8÷2 )·m2 − 2·n2 − 1 ;(3) (a4b2c) ÷ (3a2b) = (1÷3 )·a4 − 2·b2 −1·c .
仔细观察一下，并分析与思考下列几点：
(被除式的系数)÷ (除式的系数)
(被除式的指数) —(除式的指数)
单项式 的 除法 法则
如何进行单项式除以单项式的运算?
单项式相除, 把系数、同底数的幂分别相除后，作为商的因式；对于只在被除式里含有的字母，则连它的指数一起作为商的一个因式。
解： (1).(2x²y)³·(–7xy²)÷(14x4y³)
=-56x7y5 ÷(14x4y³)
解：(2).(2a+b)4÷(2a+b)²
= 4a2+4ab+b2
=8x6y3 ·(–7xy²)÷(14x4y³)
= (2a+b)4-2
(1)(-a)8÷(-a2)
(2)-5a5b3c÷5a4b3
(4)-3a2x4y3÷(-axy2)
(5)(4×109)÷(-2×103)
(3) 6m2n÷(-2mn)
( a+b+c )÷m
多项式除以单项式，
先把这个多项式的每一项分别除以单项式，
多项式除以单项式的法则
(1)(-2a4b3c)3÷(-8a4b5c)
(3 )(-3.6×1010)÷(-2×102)2÷(3×102)2
(2)(6x2y3)2÷(3xy2)2
完全平方公式(两数和的平方）
(a+b)(a-b) =
(x+a)(x+b)=
计算：（1） （2x＋3）（2x－3）（2） （－x＋2）（－x－2）（3） （－2x＋y）（2x＋y）（4） （y－x）（－x－y）
下列计算是否正确？如不正确，应如何改正？
(-x-1)(x+1) =
(a-2b+3)(a+2b-3)的结果是（ ）
=[a-(2b-3)][a+(2b-3)]
1.运用前两节所学的知识填空1).m(a+b+c)= .2).(a+b)(a-b)= .3).(a+b)2= .
2.试一试 填空:1).ma+mb+mc= m•( )2).a2-b2=( )( )3).a2+2ab+b2=( )2
一般地，把一个多项式转化成几个整式的积的形式，叫做因式分解，有时我们也把这一过程叫做分解因式。
判断哪些是因式分解? (1) x2-4y2=(x+2y)(x-2y) (2) 2x(x-3y)=2x2-6xy (3) (5a-1)2=25a2-10a+1 (4) x2+4x+4=(x+2)2 (5)(a-3)(a+3)=a2-9
像(1)这种因式分解的方法叫提公因式法
像(2),(3)利用乘法公式对多项式进行因式分解的这种因式分解的方法就称为公式法.
1) ma+mb+mc=m( a+b+c )
2) a2-b2=(a+b)(a-b )3) a2+2ab+b2=(a+b)2
1) 首选提公因式法,其次考虑公式法2)两项考虑平方差法，三项考虑完全平方公式3）因式分解要砌底4）（可用整式的乘法检验）但不走回头路
找出下列各多项式中的公因式
取每项中含有的相同字母
问:多项式中的公因式是如何确定的？
易 错 分 析
1、 把下列各式分解因式：　1）18-2b²　　　　 2) x4 –1
1.选择题：3)下列各式能用平方差公式分解因式的是（ ）4X²+y² B. 4 x- (-y)² -4 X²-y³ D. - X²+ y²4) -4a² +1分解因式的结果应是 （ ）-(4a+1)(4a-1) B. -( 2a –1)(2a –1)-(2a +1)(2a+1) D. -(2a+1) (2a-1)
1.把下列多项式因式分解1). 6x(a+2b)2-3x(a+2b)2). (b-a)2-2a+2b3). a(a-b)2+(b-a)3
1) 13.8×0.125+86.2×2) 0.73×32-0.32×633) 33+112+66
4)已知a+b=5,ab=3,求a2b+ab2的值.
3.解方程:(5x+3)(5x+6)-(5x+3)(5x+7)=0
假如用一根比地球赤道长1米的铁丝将地球赤道围起来,那么铁丝与赤道之间的间隙能有多大(地球看成球形)?猜想一只乒乓球能否穿过该间隙?(一头猪了???)
练习：分解下列各式:
（2）9m2-4n2
(2) 9m2-4n2
(　 　 ) ( 　　 )
＝(3m)2 － (2n)2
1、利用分解因式简便计算
(1) 652-642 (2) 5.42-4.62
解:652-642=(65+64)(65-64)=129×1=129
解:5.42-4.62 =(5.4+4.6)(5.4-4.6) =10×0.8 =8
3、求证:当n是整数时，两个连续奇数的平方差 (2n+1)2-(2n-1)2是8的倍数。
(a+b)2=a2+2ab+b2(a-b)2=a2-2ab+b2
a2+2ab+b2 =(a+b)2a2-2ab+b2 = (a-b)2
a2+2ab+b2 =(a+b)2a2-2ab+b2 = (a-b)2用他们可以把一个三项式分解因式的特点：两项是两个数的平方另一项是加上(或减去)这两个数积的两倍
完全平方例题讲解(1)
x2-4x+4 =x2-4x+22 =(x-2)2
a2 +2a+1= a2 +2·a·1 +12=（a+1）2
a2+10a+25
=a2+2·a( )+( )2=(a+ )2
X2+12ax+36a2
=X2+2·x·6a +(6a)2=(x+6a)2
4a2+25b2-20ab
=(2a)2 -2·2a·5b +(5b)2=(2a-5b)2
-8x2y-2x3-8xy2 =-2x(x2+4xy+4y2) =-2x(x+2y)2