2021-2022学年北师大版七年级上册数学期末模拟卷（word版 含答案）

这是一份2021-2022学年北师大版七年级上册数学期末模拟卷（word版 含答案），共15页。

2021-2022学年北师大版七年级上学期数学期末模拟卷
一．选择题（共10小题，满分30分，每小题3分）
1．（3分）若x＝1是方程﹣2mx+n﹣1＝0的解，则2019+n﹣2m的值为（　　）
A．2018 B．2019 C．2020 D．2019或2020
2．（3分）钟表上8点30分时，时针与分针的夹角为（　　）
A．15° B．30° C．75° D．60°
3．（3分）下列运算中，正确的是（　　）
A．3a+2b＝5ab B．2a3+3a2＝5a5
C．﹣4a2b+3ba2＝﹣a2b D．5a2﹣4a2＝1
4．（3分）一项工程甲单独做要40天完成，乙单独做需要60天完成，甲先单独做4天，然后甲乙两人合作x天完成这项工程，则可以列的方程是（　　）
A． B．
C． D．
5．（3分）郝炜同学在计算35+x时，误将“+”看成“﹣”，结果得10，则35+x的值应为（　　）
A．20 B．60 C．10 D．70
6．（3分）某个几何体的展开图如图所示，该几何体是（　　）

A．三棱锥 B．四棱锥 C．三棱柱 D．圆锥
7．（3分）某企业今年1月份产值为a万元，2月份比1月份减少了10%，预计3月份比2月份增加16%．则3月份的产值将达到（　　）
A．（a﹣10%）（a+16%）万元 B．（a﹣10%+16%）万元
C．a（1﹣10%）（1+16%）万元 D．a（1﹣10%+16%）万元
8．（3分）北流市某风景区的门票价格在2019年国庆期间有如下优惠：购票人数为1～50人时，每人票价格为50元；购票人数为51﹣100人时，每人门票价格45元购票人数为100人以上时，每人门票价格为40元．某初中初一有两班共103人去该风景区，如果两班都以班为单位分别购票，一共需付4860元，则两班人数分别为（　　）
A．56，47 B．57，48 C．58，45 D．59，44
9．（3分）有理数a，b，c在数轴上对应的点的位置如图所示，则下列式子正确的是（　　）

A．a＞b B．|a﹣b|＝a﹣b C．﹣a＜﹣b＜c D．b+c＞0
10．（3分）如图，点C，D为线段AB上两点，AC+BD＝8，且AD+BC＝AB，设CD＝t，则方程3x﹣7（x﹣1）＝﹣2（x+3）的解是（　　）

A．x＝2 B．x＝3 C．x＝4 D．x＝5
二．填空题（共6小题，满分18分，每小题3分）
11．（3分）已知a，b为有理数，如果规定一种新的运算“※”，规定：a※b＝3b﹣5a，例如：1※2＝3×2﹣5×1＝6﹣5＝1，计算：（2※3）※5＝　 　．
12．（3分）如图，点A、O、B在一条直线上，且∠AOD＝35°，OD平分∠AOC，则图中∠BOC＝　 　度．

13．（3分）某品牌旗舰店将某商品按进价提高40%后标价，在一次促销活动中，按标价的8折销售，售价为2240元，那么这种商品的进价为　 　元．
14．（3分）当x＝1时，多项式ax2+bx+1的值为3，那么多项式2（3a﹣b）﹣（5a﹣3b）的值为　 　．
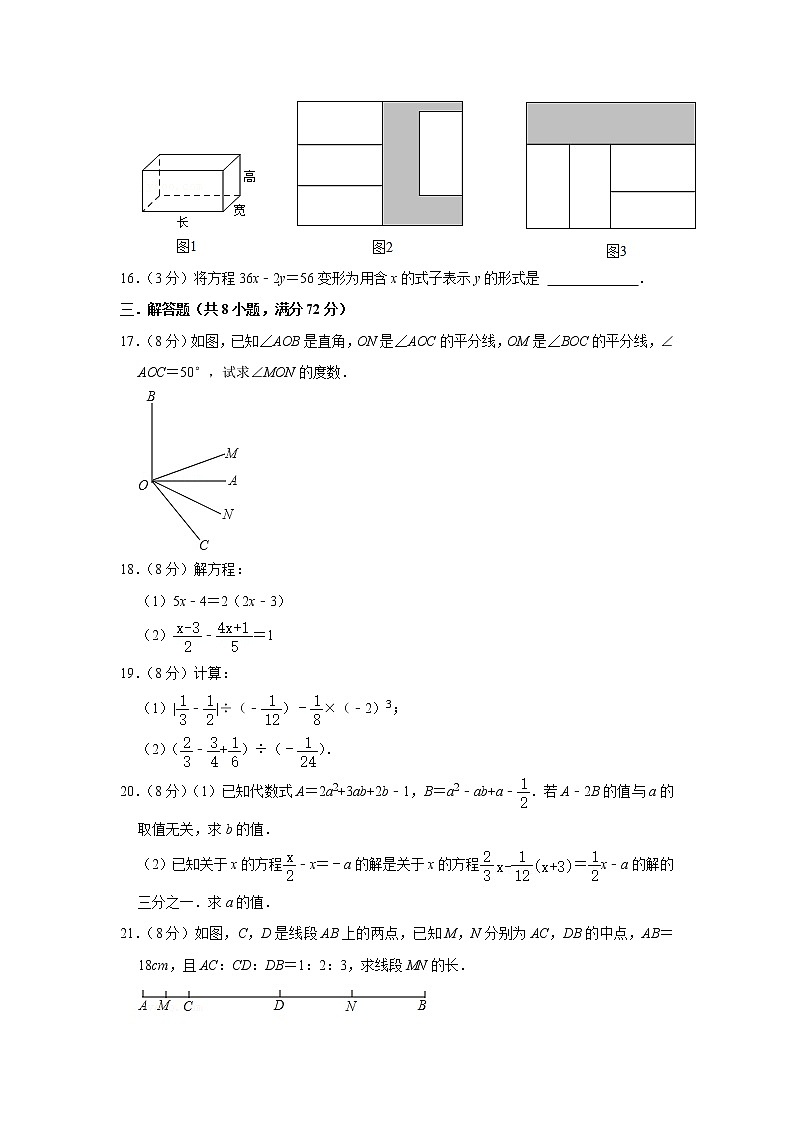
15．（3分）一件商品的包装盒是一个长方体（如图1），它的宽和高相等．小明将四个这样的包装盒放入一个长方体大纸箱中，从上面看所得图形如图2所示，大纸箱底面长方形未被覆盖的部分用阴影表示．接着小明将这四个包装盒又换了一种摆放方式，从上面看所得图形如图3所示，大纸箱底面未被覆盖的部分也用阴影表示．
设图1中商品包装盒的宽为a，则商品包装盒的长为　 　，图2中阴影部分的周长与图3中阴影部分的周长的差为　 　（都用含a的式子表示）．

16．（3分）将方程36x﹣2y＝56变形为用含x的式子表示y的形式是 　 　．
三．解答题（共8小题，满分72分）
17．（8分）如图，已知∠AOB是直角，ON是∠AOC的平分线，OM是∠BOC的平分线，∠AOC＝50°，试求∠MON的度数．

18．（8分）解方程：
（1）5x﹣4＝2（2x﹣3）
（2）﹣＝1
19．（8分）计算：
（1）|﹣|÷（﹣）﹣×（﹣2）3；
（2）（﹣+）÷（﹣）．
20．（8分）（1）已知代数式A＝2a2+3ab+2b﹣1，B＝a2﹣ab+a﹣．若A﹣2B的值与a的取值无关，求b的值．
（2）已知关于x的方程﹣x＝﹣a的解是关于x的方程＝x﹣a的解的三分之一．求a的值．
21．（8分）如图，C，D是线段AB上的两点，已知M，N分别为AC，DB的中点，AB＝18cm，且AC：CD：DB＝1：2：3，求线段MN的长．

22．（10分）为打造运河风光带，现有一段河道治理任务由A、B两个工程队完成．A工程队单独治理该河道需16天完成，B工程队单独治理该河道需24天完成，现在A工程队单独做6天后，B工程队加入合作完成剩下的工程，问B工程队工作了多少天？
23．（10分）如图1，在一条可以折叠的数轴上，点A，B分别表示数﹣9和4．

（1）A，B两点之间的距离为　 　．
（2）如图2，如果以点C为折点，将这条数轴向右对折，此时点A落在点B的右边1个单位长度处，则点C表示的数是　 　
（3）如图1，若点A以每秒3个单位长度的速度沿数轴向右运动，点B以每秒2个单位长度的速度也沿数轴向右运动，那么经过多少时间，A．B两点相距4个单位长度？
24．（12分）如图所示，O为直线上的一点，且∠COD为直角，OE平分∠BOD，OF平分∠AOE，∠BOC+∠FOD＝117°，求∠BOE的度数．















2021-2022学年北师大版七年级上学期数学期末模拟卷
一．选择题（共10小题，满分30分，每小题3分）
1．（3分）若x＝1是方程﹣2mx+n﹣1＝0的解，则2019+n﹣2m的值为（　　）
A．2018 B．2019 C．2020 D．2019或2020
【答案】C
【解析】把x＝1代入方程得：﹣2m+n﹣1＝0，
整理得：2m﹣n＝﹣1，
则原式＝2019+n﹣2m
＝2019﹣（2m﹣n）
＝2019﹣（﹣1）
＝2019+1
＝2020，
故选：C．
2．（3分）钟表上8点30分时，时针与分针的夹角为（　　）
A．15° B．30° C．75° D．60°
【答案】C
【解析】∵8点30分，时针在8和9正中间，分针指向6，中间相差两个半大格，而钟表12个数字，每相邻两个数字之间的夹角为30°，
∴8点30分时，时针与分针的夹角的度数为：30°×2.5＝75°．
故选：C．
3．（3分）下列运算中，正确的是（　　）
A．3a+2b＝5ab B．2a3+3a2＝5a5
C．﹣4a2b+3ba2＝﹣a2b D．5a2﹣4a2＝1
【答案】C
【解析】A、3a与2b不是同类项，不能合并，此选项错误；
B、2a3与3a2不是同类项，不能合并，此选项错误；
C、﹣4a2b+3ba2＝﹣a2b，此选正确；
D、5a2﹣4a2＝a2，此选项错误；
故选：C．
4．（3分）一项工程甲单独做要40天完成，乙单独做需要60天完成，甲先单独做4天，然后甲乙两人合作x天完成这项工程，则可以列的方程是（　　）
A． B．
C． D．
【答案】C
【解析】设整个工程为1，根据关系式甲完成的部分+两人共同完成的部分＝1列出方程式为：
．
故选：C．
5．（3分）郝炜同学在计算35+x时，误将“+”看成“﹣”，结果得10，则35+x的值应为（　　）
A．20 B．60 C．10 D．70
【答案】B
【解析】35+（35﹣10）
＝35+25
＝60．
故选：B．
6．（3分）某个几何体的展开图如图所示，该几何体是（　　）

A．三棱锥 B．四棱锥 C．三棱柱 D．圆锥
【答案】C
【解析】三个长方形和两个等腰三角形折叠后，能围成的几何体是三棱柱．
故选：C．
7．（3分）某企业今年1月份产值为a万元，2月份比1月份减少了10%，预计3月份比2月份增加16%．则3月份的产值将达到（　　）
A．（a﹣10%）（a+16%）万元 B．（a﹣10%+16%）万元
C．a（1﹣10%）（1+16%）万元 D．a（1﹣10%+16%）万元
【答案】C
【解析】由题意可得：
3月份的产值将达到：a（1﹣10%）（1+16%）（万元）．
故选：C．
8．（3分）北流市某风景区的门票价格在2019年国庆期间有如下优惠：购票人数为1～50人时，每人票价格为50元；购票人数为51﹣100人时，每人门票价格45元购票人数为100人以上时，每人门票价格为40元．某初中初一有两班共103人去该风景区，如果两班都以班为单位分别购票，一共需付4860元，则两班人数分别为（　　）
A．56，47 B．57，48 C．58，45 D．59，44
【答案】C
【解析】设人数较少的班级有x人，则人数较多的班级有（103﹣x）人，
∵4860÷45＝108（人），108＞103，
∴1＜x≤50．
依题意，得：50x+45（103﹣x）＝4860，
解得：x＝45，
∴103﹣x＝58．
故选：C．
9．（3分）有理数a，b，c在数轴上对应的点的位置如图所示，则下列式子正确的是（　　）

A．a＞b B．|a﹣b|＝a﹣b C．﹣a＜﹣b＜c D．b+c＞0
【答案】D
【解析】由题意，可知a＜b＜0＜c，|a|＝|c|＞|b|．
A、∵a＜b＜0＜c，∴a＞b错误，本选项不符合题意；
B、∵a＜b，∴a﹣b＜0，∴|a﹣b|＝﹣﹣a+b，∴|a﹣b|＝a﹣b错误，本选项不符合题意；
C、∵a＜b＜0＜c，|a|＝|c|＞|b|，∴﹣a＜﹣b＜c错误，本选项不符合题意；
D、∵b＜0＜c，|c|＞|b|，∴c+b＜0，正确，本选项符合题意．
故选：D．
10．（3分）如图，点C，D为线段AB上两点，AC+BD＝8，且AD+BC＝AB，设CD＝t，则方程3x﹣7（x﹣1）＝﹣2（x+3）的解是（　　）

A．x＝2 B．x＝3 C．x＝4 D．x＝5
【答案】D
【解析】∵AD+BC＝AB＝AC+CD+BD+CD，AC+BD＝8，AB＝AC+BD+CD，
∴（8+CD）＝2CD+8，
解得：CD＝6．
∴3x﹣7（x﹣1）＝3﹣2（x+3）的解为x＝5，
故选：D．
二．填空题（共6小题，满分18分，每小题3分）
11．（3分）已知a，b为有理数，如果规定一种新的运算“※”，规定：a※b＝3b﹣5a，例如：1※2＝3×2﹣5×1＝6﹣5＝1，计算：（2※3）※5＝________．
【答案】20．
【解析】（2※3）※5
＝（3×3﹣5×2）※5
＝（9﹣10）※5
＝（﹣1）※5
＝3×5﹣5×（﹣1）
＝15+5
＝20．
12．（3分）如图，点A、O、B在一条直线上，且∠AOD＝35°，OD平分∠AOC，则图中∠BOC＝________度．

【答案】110．
【解析】∵OD平分∠AOC，∠AOD＝35°，
∴∠AOC＝2∠AOD＝2×35°＝70°，
∵∠AOC与∠BOC是邻补角，
∴∠AOC+∠BOC＝180°，
∴∠BOC＝180°﹣70°＝110°．
13．（3分）某品牌旗舰店将某商品按进价提高40%后标价，在一次促销活动中，按标价的8折销售，售价为2240元，那么这种商品的进价为________元．
【答案】2000．
【解析】设这种商品的进价是x元，根据题意可以列出方程：
由题意得，（1+40%）x×0.8＝2240．
解得：x＝2000，
14．（3分）当x＝1时，多项式ax2+bx+1的值为3，那么多项式2（3a﹣b）﹣（5a﹣3b）的值为________．
【答案】2．
【解析】把x＝1代入多项式得：原式＝a+b+1＝3，即a+b＝2，
则原式＝6a﹣2b﹣5a+3b＝a+b＝2，
15．（3分）一件商品的包装盒是一个长方体（如图1），它的宽和高相等．小明将四个这样的包装盒放入一个长方体大纸箱中，从上面看所得图形如图2所示，大纸箱底面长方形未被覆盖的部分用阴影表示．接着小明将这四个包装盒又换了一种摆放方式，从上面看所得图形如图3所示，大纸箱底面未被覆盖的部分也用阴影表示．
设图1中商品包装盒的宽为a，则商品包装盒的长为________，图2中阴影部分的周长与图3中阴影部分的周长的差为________（都用含a的式子表示）．

【答案】2a，2a．
【解析】根据摆放情况可得，包装盒的一个长等于两个宽，即长为2a，
大纸箱的长为4a，宽为3a，
图2中阴影部分的周长为：3a×2+2a×2+2a＝12a，
图3中阴影部分的周长为：4a×2+2a＝10a，
图2与图3周长的差为12a﹣10a＝2a，
16．（3分）将方程36x﹣2y＝56变形为用含x的式子表示y的形式是________．
【答案】y＝18x﹣28．
【解析】∵36x﹣2y＝56，
∴2y＝36x﹣56，
∴y＝18x﹣28，
三．解答题（共8小题，满分72分）
17．（8分）如图，已知∠AOB是直角，ON是∠AOC的平分线，OM是∠BOC的平分线，∠AOC＝50°，试求∠MON的度数．

【答案】见解析
【解析】∵∠AOB是直角，∠AOC＝50°，
∴∠BOC＝∠AOB+∠AOC＝90°+50°＝140°，
∵OM是∠BOC的平分线，ON是∠AOC的平分线，
∴∠MOC＝∠BOC＝＝70°，∠NOC＝∠AOC＝＝25°，
∴∠MON＝∠MOC﹣∠NOC＝70°﹣25°＝45°．
18．（8分）解方程：
（1）5x﹣4＝2（2x﹣3）
（2）﹣＝1
【答案】见解析
【解析】（1）去括号得：5x﹣4＝4x﹣6，
移项合并得：x＝﹣2；
（2）去分母得：5x﹣15﹣8x﹣2＝10，
移项合并得：﹣3x＝27，
解得：x＝﹣9．
19．（8分）计算：
（1）|﹣|÷（﹣）﹣×（﹣2）3；
（2）（﹣+）÷（﹣）．
【答案】见解析
【解析】（1）|﹣|÷（﹣）﹣×（﹣2）3
＝÷（﹣）﹣×（﹣8）
＝﹣2+1
＝﹣1．

（2）（﹣+）÷（﹣）
＝×（﹣24）﹣×（﹣24）+×（﹣24）
＝﹣16+18﹣4
＝﹣2．
20．（8分）（1）已知代数式A＝2a2+3ab+2b﹣1，B＝a2﹣ab+a﹣．若A﹣2B的值与a的取值无关，求b的值．
（2）已知关于x的方程﹣x＝﹣a的解是关于x的方程＝x﹣a的解的三分之一．求a的值．
【答案】见解析
【解析】（1）∵A＝2a2+3ab+2b﹣1，B＝a2﹣ab+a﹣，
∴A﹣2B＝2a2+3ab+2b﹣1﹣2（a2﹣ab+a﹣）
＝2a2+3ab+2b﹣1﹣2a2+2ab﹣2a+1
＝5ab﹣2a+2b；
∵A﹣2B＝（5b﹣2）a+2b，代数式的值与a的取值无关，
∴5b﹣2＝0，
∴b＝；
（2）解方程﹣x＝﹣a得，x＝2a，解方程得，x＝3﹣12a，
∵关于x的方程﹣x＝﹣a的解是关于x的方程的解的三分之一，
∴2a＝（3﹣12a），
解得a＝．
21．（8分）如图，C，D是线段AB上的两点，已知M，N分别为AC，DB的中点，AB＝18cm，且AC：CD：DB＝1：2：3，求线段MN的长．

【答案】见解析
【解析】设AC，CD，DB的长分别为xcm，2xcm，3xcm
∵AC+CD+DB＝AB，AB＝18cm
∴x+2x+3x＝18
解得x＝3
∴AC＝3cm，CD＝6cm，DB＝9cm
∵M，N为AC，DB的中点，
∴
∴MN＝MC+CD+DN＝12cm，
∴MN的长为12cm．
22．（10分）为打造运河风光带，现有一段河道治理任务由A、B两个工程队完成．A工程队单独治理该河道需16天完成，B工程队单独治理该河道需24天完成，现在A工程队单独做6天后，B工程队加入合作完成剩下的工程，问B工程队工作了多少天？
【答案】见解析
【解析】设B工程队工作了x天，由题意得：，
解这个方程得：x＝6
经检验：x＝6符合题意．
答：B工程队工作了6天．
23．（10分）如图1，在一条可以折叠的数轴上，点A，B分别表示数﹣9和4．

（1）A，B两点之间的距离为　13　．
（2）如图2，如果以点C为折点，将这条数轴向右对折，此时点A落在点B的右边1个单位长度处，则点C表示的数是________
（3）如图1，若点A以每秒3个单位长度的速度沿数轴向右运动，点B以每秒2个单位长度的速度也沿数轴向右运动，那么经过多少时间，A．B两点相距4个单位长度？
【答案】见解析
【解析】（1）4﹣（﹣9）＝13．
故答案为：13．
（2）设点C表示的数为x，则AC＝x﹣（﹣9），BC＝4﹣x，
依题意，得：x﹣（﹣9）＝4﹣x+1，
解得：x＝﹣2．
故答案为：﹣2．
（3）当运动时间为t秒时，点A表示的数为3t﹣9，点B表示的数为2t+4．
∵AB＝4，
∴3t﹣9﹣（2t+4）＝4或2t+4﹣（3t﹣9）＝4，
解得：t＝9或t＝17．
答：经过9秒或17秒时，A．B两点相距4个单位长度．
24．（12分）如图所示，O为直线上的一点，且∠COD为直角，OE平分∠BOD，OF平分∠AOE，∠BOC+∠FOD＝117°，求∠BOE的度数．

【答案】见解析
【解析】设∠BOE＝α°，
∵OE平分∠BOD，
∴∠BOD＝2α°，∠EOD＝α°．
∵∠COD＝∠BOD+∠BOC＝90°，
∴∠BOC＝90°﹣2α°．
∵OF平分∠AOE，∠AOE+∠BOE＝180°，
∴∠FOE＝∠AOE＝（180°﹣α°）＝90°﹣α°，
∴∠FOD＝∠FOE﹣∠EOD＝90°﹣α°﹣α°＝90°﹣α°，
∵∠BOC+∠FOD＝117°，
∴90°﹣2α°+90°﹣α°＝117°，
∴α＝18，
∴∠BOE＝18°．