

2021-2022学年北师大版七年级上册数学期末模拟卷(2)(word版 含答案)
展开2021-2022学年北师大版七年级上学期数学期末模拟卷(2)
一.选择题(共10小题,满分30分,每小题3分)
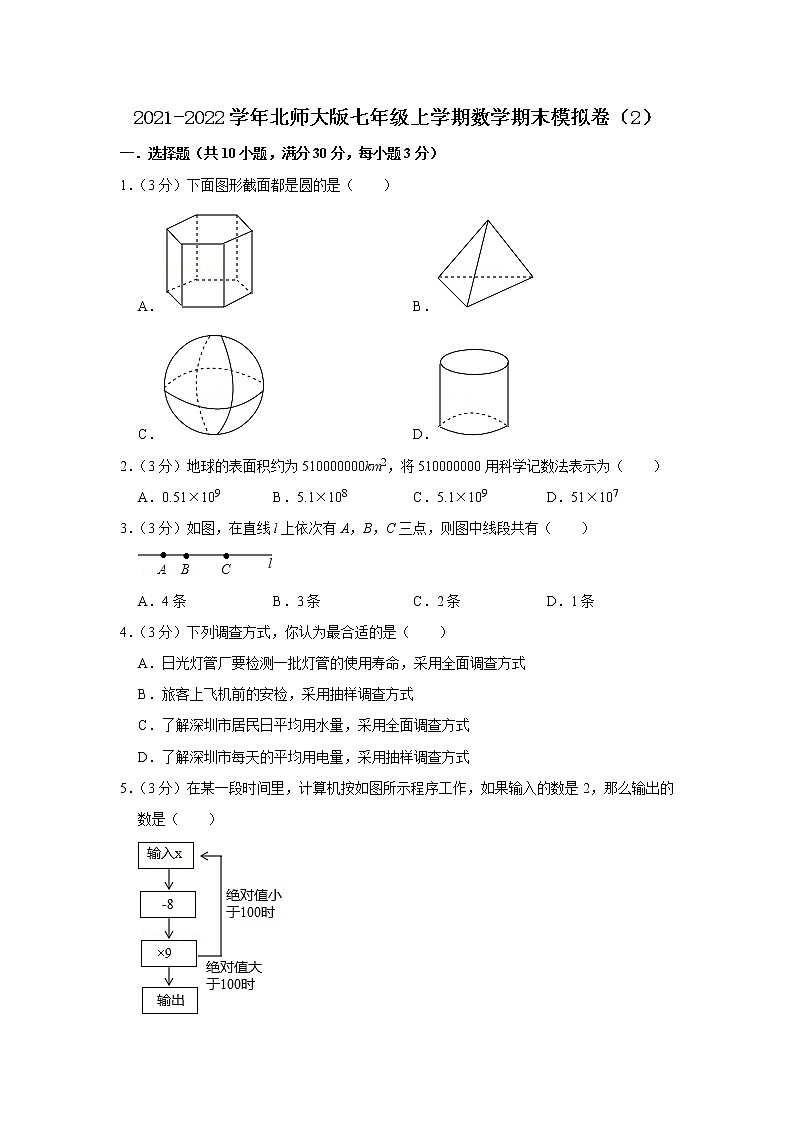
1.(3分)下面图形截面都是圆的是( )
A. B.
C. D.
2.(3分)地球的表面积约为510000000km2,将510000000用科学记数法表示为( )
A.0.51×109 B.5.1×108 C.5.1×109 D.51×107
3.(3分)如图,在直线l上依次有A,B,C三点,则图中线段共有( )
A.4条 B.3条 C.2条 D.1条
4.(3分)下列调查方式,你认为最合适的是( )
A.日光灯管厂要检测一批灯管的使用寿命,采用全面调查方式
B.旅客上飞机前的安检,采用抽样调查方式
C.了解深圳市居民日平均用水量,采用全面调查方式
D.了解深圳市每天的平均用电量,采用抽样调查方式
5.(3分)在某一段时间里,计算机按如图所示程序工作,如果输入的数是2,那么输出的数是( )
A.﹣54 B.54 C.﹣558 D.558
6.(3分)居民消费价格指数是一个反映居民家庭一般所购买的消费品和服务项目价格水平变动情况的宏观经济指标.据统计,从2018年9月到2019年8月,全国居民消费价格每月比上个月的增长率如图所示:
根据上图提供的信息,下列推断中不合理的是( )
A.2018年12月的增长率为0.0%,说明与2018年11月相比,全国居民消费价格保持不变
B.2018年11月与2018年10月相比,全国居民消费价格降低0.3%
C.2018年9月到2019年8月,全国居民消费价格每月比上个月的增长率中最小的是﹣0.4%
D.2019年1月到2019年8月,全国居民消费价格每月比上个月的增长率一直持续变大
7.(3分)一个两位数,个位数字为a,十位数字比个位数字小1,则这个两位数可表示为( )
A.11a+1 B.11a﹣1 C.11a+10 D.11a﹣10
8.(3分)下列说法中,正确的是( )
A.1.45°=87′
B.1800″=30°
C.当时钟指向3:30时,时针与分钟的夹角是90°
D.两个锐角的和一定是钝角
9.(3分)对如图所示的几何体认识正确的是( )
A.几何体是四棱柱 B.棱柱的侧面是三角形
C.棱柱的底面是四边形 D.棱柱的底面是三角形
10.(3分)已知A地的海拔高度为﹣36米,B地比A地高20米,则B地的海拔高度为( )
A.16米 B.20米 C.﹣16米 D.﹣56米
二.填空题(共5小题,满分15分,每小题3分)
11.(3分)某城市11月份一天中的最高气温为12℃,当天的日温差是15℃,这一天的最低气温是 ℃.
12.(3分)下列有四个生活、生产现象:①有两个钉子就可以把木条固定在墙上;②从A地到B地架设电线,总是尽可能沿着线段AB架设;③植树时,只要定出两棵树的位置,就能确定同一行所在的直线;④把弯曲的公路改直,就能缩短路程,其中可用基本事实“两点之间,线段最短”来解释的现象有 .
13.(3分)扬州雕版印刷技艺历史悠久,元代数学家朱世杰的《算学启蒙》一书曾刻于扬州,该书是中国较早的数学著作之一,书中记载一道问题:“今有良马日行二百四十里,驽马日行一百五十里,驽马先行一十二日,问良马几何日追及之?”题意是:快马每天走240里,慢马每天走150里,慢马先走12天,试问快马几天追上慢马?答:快马 天追上慢马.
14.(3分)如图是一组有规律的图案,它们是由边长相同的正方形和正三角形拼接而成,第①个图案有4个三角形和1个正方形,第②个图案有7个三角形和2个正方形,第③个图案有10个三角形和3个正方形,…依此规律,如果第n个图案中正三角形和正方形的个数共有2021个,则n= .
15.(3分)按下面的程序计算:
如果输入x的值是正整数,输出结果是150,那么满足条件的x的值有 个.
三.解答题(共7小题,满分55分)
16.(6分)下面已给出了如图几何体的主视图,请补画出该几何体的左视图和俯视图.
17.(7分)先化简,再求值:5(3a2b﹣ab2)﹣4(﹣ab2+3a2b),其中a=,b=﹣4.
18.(7分)已知下列有理数:0,(﹣2)2,﹣|﹣4|,﹣,﹣(﹣1)
(1)计算:(﹣2)2= ,﹣|﹣4|= ,﹣(﹣1)= ;
(2)这些数中,所有负数的和的绝对值是 .
(3)把下面的直线补充成一条数轴,在数轴上描出表示0,(﹣2)2,﹣|﹣4|,﹣,﹣(﹣1)这些数的点,并把这些数标在对应点的上方.
19.(8分)某校学生会发现同学们就餐时剩余饭菜较多,浪费严重,于是准备在校内倡导“光盘行动”,让同学们珍惜粮食,为了让同学们理解这次活动的重要性,校学生会在某天午餐后,随机调查了部分同学这餐饭菜的剩余情况,并将结果统计后绘制成了如图所示的不完整的统计图.
(1)这次被调查的同学共有 人;
(2)补全条形统计图,并在图上标明相应的数据;
(3)校学生会通过数据分析,估计这次被调查的所有学生一餐浪费的食物可以供50人食用一餐.据此估算,该校18000名学生一餐浪费的食物可供多少人食用一餐.
20.(8分)【问题】用n边形的对角线把n边形分割成(n﹣2)个三角形,共有多少种不同的分割方案(n≥4)?
【探究】为了解决上面的数学问题,我们采取一般问题特殊化的策略,先从最简单情形入手,再逐次递进转化,最后猜想得出结论.不妨假设n边形的分割方案有Pn种.
探究一:用四边形的对角线把四边形分割成2个三角形,共有多少种不同的分割方案?如图①,图②,显然,只有2种不同的分割方案.所以,P4=2.
探究二:用五边形的对角线把五边形分割成3个三角形,共有多少种不同的分割方案?
不妨把分割方案分成三类:
第1类:如图③,用A,E与B连接,先把五边形分割转化成1个三角形和1个四边形,再把四边形分割成2个三角形,由探究一知,有P4种不同的分割方案,所以,此类共有P4种不同的分割方案.
第2类:如图④,用A,E与C连接,把五边形分割成3个三角形,有1种不同的分割方案,可视为P4种分割方案.
第3类:如图⑤,用A,E与D连接,先把五边形分割转化成1个三角形和1个四边形,再把四边形分割成2个三角形,由探究一知,有P4种不同的分割方案,所以,此类共有P4种不同的分割方案.
所以,P5=P4+P4+P4=×P4=×P4=5(种)
探究三:用六边形的对角线把六边形分割成4个三角形,共有多少种不同的分割方案?
不妨把分割方案分成四类:
第1类:如图⑥,用A,F与B连接,先把六边形分割转化成1个三角形和1个五边形,再把五边形分割成3个三角形,由探究二知,有P5种不同的分割方案,所以,此类共有P5种不同的分割方案.
第2类:如图⑦,用A,F与C连接,先把六边形分割转化成2个三角形和1个四边形.再把四边形分割成2个三角形,由探究一知,有P4种不同的分割方案.所以,此类共有P4种分割方案.
第3类:如图⑧,用A,F与D连接,先把六边形分割转化成2个三角形和1个四边形.再把四边形分割成2个三角形,由探究一知,有P4种不同的分割方案.所以,此类共有P4种分割方案.
第4类:如图⑨,用A,F与E连接,先把六边形分割转化成1个三角形和1个五边形.再把五边形分割成3个三角形,由探究二知,有P5种不同的分割方案.所以,此类共有P5种分割方案.
所以,P6=P5+P4+P4+P5=P5+P5+P5+P5=P5=14(种)
探究四:用七边形的对角线把七边形分割成5个三角形,则P7与P6的关系为:P7= ×P6,共有 种不同的分割方案.
【结论】用n边形的对角线把n边形分割成(n﹣2)个三角形,共有多少种不同的分割方案(n≥4)?(直接写出Pn与Pn﹣1的关系式,不写解答过程).
【应用】用九边形的对角线把九边形分割成7个三角形,共有多少种不同的分割方案?(应用上述结论,写出解答过程)
21.(9分)如图,已知OE是∠AOC的角平分线,OD是∠BOC的角平分线.
(1)若∠AOC=120°,∠BOC=30°,求∠DOE的度数;
(2)若∠AOB=90°,∠BOC=α,求∠DOE的度数.
22. (10分)A、B两地相距15千米,甲汽车在前边以50千米/小时从A出发,乙汽车在后边以40千米/小时从B出发,两车同时出发同向而行(沿BA方向),问经过几小时,两车相距30千米
2021-2022学年北师大版七年级上学期数学期末模拟卷(2)
一.选择题(共10小题,满分30分,每小题3分)
1.(3分)下面图形截面都是圆的是( )
A. B.
C. D.
【答案】C
【解析】将一个平面从任意角度去截球,都会得到一个圆.
故选:C.
2.(3分)地球的表面积约为510000000km2,将510000000用科学记数法表示为( )
A.0.51×109 B.5.1×108 C.5.1×109 D.51×107
【答案】B
【解析】510000000=5.1×108,
故选:B.
3.(3分)如图,在直线l上依次有A,B,C三点,则图中线段共有( )
A.4条 B.3条 C.2条 D.1条
【答案】B
【解析】图中线段共有AB、AC、BC三条,
故选:B.
4.(3分)下列调查方式,你认为最合适的是( )
A.日光灯管厂要检测一批灯管的使用寿命,采用全面调查方式
B.旅客上飞机前的安检,采用抽样调查方式
C.了解深圳市居民日平均用水量,采用全面调查方式
D.了解深圳市每天的平均用电量,采用抽样调查方式
【答案】D
【解析】A、日光灯管厂要检测一批灯管的使用寿命,应用抽样调查,故A错误;
B、旅客上飞机前的安检,采用普查方式,故B错误;
C、了解深圳市居民日平均用水量,采用抽样调查方式,故C错误;
D、了解深圳市每天的平均用电量,采用抽样调查方式,故D正确.
故选:D.
5.(3分)在某一段时间里,计算机按如图所示程序工作,如果输入的数是2,那么输出的数是( )
A.﹣54 B.54 C.﹣558 D.558
【答案】C
【解析】把x=2代入计算程序中得:(2﹣8)×9=﹣54,
把x=﹣54代入计算程序中得:(﹣54﹣8)×9=﹣558,
则输出结果为﹣558,
故选:C.
6.(3分)居民消费价格指数是一个反映居民家庭一般所购买的消费品和服务项目价格水平变动情况的宏观经济指标.据统计,从2018年9月到2019年8月,全国居民消费价格每月比上个月的增长率如图所示:
根据上图提供的信息,下列推断中不合理的是( )
A.2018年12月的增长率为0.0%,说明与2018年11月相比,全国居民消费价格保持不变
B.2018年11月与2018年10月相比,全国居民消费价格降低0.3%
C.2018年9月到2019年8月,全国居民消费价格每月比上个月的增长率中最小的是﹣0.4%
D.2019年1月到2019年8月,全国居民消费价格每月比上个月的增长率一直持续变大
【答案】D
【解析】由统计图可知,
2018年12月的增长率为0.0%,说明与2018年11月相比,全国居民消费价格保持不变,故选项A合理;
2018年11月与2018年10月相比,全国居民消费价格降低0.3%,故选项B合理;
2018年9月到2019年8月,全国居民消费价格每月比上个月的增长率中最小的是﹣0.4%,故选项C合理;
2019年1月到2019年8月,全国居民消费价格每月比上个月的增长率先增大,后减小,再增大,故选项D不合理;
故选:D.
7.(3分)一个两位数,个位数字为a,十位数字比个位数字小1,则这个两位数可表示为( )
A.11a+1 B.11a﹣1 C.11a+10 D.11a﹣10
【答案】D
【解析】根据题意知十位数字为a﹣1,
则这个两位数为10(a﹣1)+a=11a﹣10,
故选:D.
8.(3分)下列说法中,正确的是( )
A.1.45°=87′
B.1800″=30°
C.当时钟指向3:30时,时针与分钟的夹角是90°
D.两个锐角的和一定是钝角
【答案】A
【解析】A、1.45°=87′,故A正确;
B、1800″=30′=0.5°,故B错误;
C、当时钟指向3:30时,时针与分钟的夹角是75°,故C错误;
D、两个锐角的和可能是锐角、可能是钝角,故D错误;
故选:A.
9.(3分)对如图所示的几何体认识正确的是( )
A.几何体是四棱柱 B.棱柱的侧面是三角形
C.棱柱的底面是四边形 D.棱柱的底面是三角形
【答案】D
【解析】由图可知,该几何体是三棱柱,
∴底面是三角形,侧面是四边形,
故选:D.
10.(3分)已知A地的海拔高度为﹣36米,B地比A地高20米,则B地的海拔高度为( )
A.16米 B.20米 C.﹣16米 D.﹣56米
【答案】C
【解析】﹣36+20=﹣16(米),
故选:C.
二.填空题(共5小题,满分15分,每小题3分)
11.(3分)某城市11月份一天中的最高气温为12℃,当天的日温差是15℃,这一天的最低气温是________℃.
【答案】﹣3.
【解析】由题意得:12﹣15=﹣3,
12.(3分)下列有四个生活、生产现象:①有两个钉子就可以把木条固定在墙上;②从A地到B地架设电线,总是尽可能沿着线段AB架设;③植树时,只要定出两棵树的位置,就能确定同一行所在的直线;④把弯曲的公路改直,就能缩短路程,其中可用基本事实“两点之间,线段最短”来解释的现象有________.
【答案】②④.
【解析】①③现象可以用两点可以确定一条直线来解释;
②④现象可以用两点之间,线段最短来解释.
13.(3分)扬州雕版印刷技艺历史悠久,元代数学家朱世杰的《算学启蒙》一书曾刻于扬州,该书是中国较早的数学著作之一,书中记载一道问题:“今有良马日行二百四十里,驽马日行一百五十里,驽马先行一十二日,问良马几何日追及之?”题意是:快马每天走240里,慢马每天走150里,慢马先走12天,试问快马几天追上慢马?答:快马________天追上慢马.
【答案】20.
【解析】设快马行x天追上慢马,则此时慢马行了(x+12)日,
依题意,得:240x=150(x+12),
解得:x=20,
∴快马20天追上慢马,
14.(3分)如图是一组有规律的图案,它们是由边长相同的正方形和正三角形拼接而成,第①个图案有4个三角形和1个正方形,第②个图案有7个三角形和2个正方形,第③个图案有10个三角形和3个正方形,…依此规律,如果第n个图案中正三角形和正方形的个数共有2021个,则n=________.
【答案】505.
【解析】因为第①个图案有4个三角形和1个正方形,
第②个图案有7个三角形和2个正方形,
第③个图案有10个三角形和3个正方形,
…
依此规律,
所以第n个图案中正三角形和正方形的个数:3n+1+n=4n+1,
4n+1=2021,
则n=505.
15.(3分)按下面的程序计算:
如果输入x的值是正整数,输出结果是150,那么满足条件的x的值有________个.
【答案】3
【解析】当4x﹣2=150时,
x=38;
当4x﹣2=38时,
x=10;
当4x﹣2=10时,
x=3,
由于4x﹣2=3,x不是正整数,不合题意.
即当x=3、10、38时,输出的结果都是150.
三.解答题(共7小题,满分55分)
16.(6分)下面已给出了如图几何体的主视图,请补画出该几何体的左视图和俯视图.
【答案】见解析
【解析】如图所示:
17.(7分)先化简,再求值:5(3a2b﹣ab2)﹣4(﹣ab2+3a2b),其中a=,b=﹣4.
【答案】见解析
【解析】原式=15a2b﹣5ab2+4ab2﹣12a2b=3a2b﹣ab2,
当a=,b=﹣4时,原式=﹣3﹣8=﹣11.
18.(7分)已知下列有理数:0,(﹣2)2,﹣|﹣4|,﹣,﹣(﹣1)
(1)计算:(﹣2)2=________,﹣|﹣4|=________,﹣(﹣1)=________;
(2)这些数中,所有负数的和的绝对值是________.
(3)把下面的直线补充成一条数轴,在数轴上描出表示0,(﹣2)2,﹣|﹣4|,﹣,﹣(﹣1)这些数的点,并把这些数标在对应点的上方.
【答案】见解析
【解析】(1)(﹣2)2=4,﹣|﹣4|=﹣4,﹣(﹣1)=1;
(2)负数为﹣|﹣4|、﹣,
则所有负数的和的绝对值=|﹣4﹣|=;
故答案为4,﹣4,1;;
(3)
19.(8分)某校学生会发现同学们就餐时剩余饭菜较多,浪费严重,于是准备在校内倡导“光盘行动”,让同学们珍惜粮食,为了让同学们理解这次活动的重要性,校学生会在某天午餐后,随机调查了部分同学这餐饭菜的剩余情况,并将结果统计后绘制成了如图所示的不完整的统计图.
(1)这次被调查的同学共有________人;
(2)补全条形统计图,并在图上标明相应的数据;
(3)校学生会通过数据分析,估计这次被调查的所有学生一餐浪费的食物可以供50人食用一餐.据此估算,该校18000名学生一餐浪费的食物可供多少人食用一餐.
【答案】见解析
【解析】(1)这次被调查的学生共有600÷60%=1000人,
故答案为:1000;
(2)剩少量的人数为1000﹣(600+150+50)=200人,
补全条形图如下:
(3),
答:估计该校18000名学生一餐浪费的食物可供900人食用一餐.
20.(8分)【问题】用n边形的对角线把n边形分割成(n﹣2)个三角形,共有多少种不同的分割方案(n≥4)?
【探究】为了解决上面的数学问题,我们采取一般问题特殊化的策略,先从最简单情形入手,再逐次递进转化,最后猜想得出结论.不妨假设n边形的分割方案有Pn种.
探究一:用四边形的对角线把四边形分割成2个三角形,共有多少种不同的分割方案?如图①,图②,显然,只有2种不同的分割方案.所以,P4=2.
探究二:用五边形的对角线把五边形分割成3个三角形,共有多少种不同的分割方案?
不妨把分割方案分成三类:
第1类:如图③,用A,E与B连接,先把五边形分割转化成1个三角形和1个四边形,再把四边形分割成2个三角形,由探究一知,有P4种不同的分割方案,所以,此类共有P4种不同的分割方案.
第2类:如图④,用A,E与C连接,把五边形分割成3个三角形,有1种不同的分割方案,可视为P4种分割方案.
第3类:如图⑤,用A,E与D连接,先把五边形分割转化成1个三角形和1个四边形,再把四边形分割成2个三角形,由探究一知,有P4种不同的分割方案,所以,此类共有P4种不同的分割方案.
所以,P5=P4+P4+P4=×P4=×P4=5(种)
探究三:用六边形的对角线把六边形分割成4个三角形,共有多少种不同的分割方案?
不妨把分割方案分成四类:
第1类:如图⑥,用A,F与B连接,先把六边形分割转化成1个三角形和1个五边形,再把五边形分割成3个三角形,由探究二知,有P5种不同的分割方案,所以,此类共有P5种不同的分割方案.
第2类:如图⑦,用A,F与C连接,先把六边形分割转化成2个三角形和1个四边形.再把四边形分割成2个三角形,由探究一知,有P4种不同的分割方案.所以,此类共有P4种分割方案.
第3类:如图⑧,用A,F与D连接,先把六边形分割转化成2个三角形和1个四边形.再把四边形分割成2个三角形,由探究一知,有P4种不同的分割方案.所以,此类共有P4种分割方案.
第4类:如图⑨,用A,F与E连接,先把六边形分割转化成1个三角形和1个五边形.再把五边形分割成3个三角形,由探究二知,有P5种不同的分割方案.所以,此类共有P5种分割方案.
所以,P6=P5+P4+P4+P5=P5+P5+P5+P5=P5=14(种)
探究四:用七边形的对角线把七边形分割成5个三角形,则P7与P6的关系为:P7=________×P6,共有________种不同的分割方案.
【结论】用n边形的对角线把n边形分割成(n﹣2)个三角形,共有多少种不同的分割方案(n≥4)?(直接写出Pn与Pn﹣1的关系式,不写解答过程).
【应用】用九边形的对角线把九边形分割成7个三角形,共有多少种不同的分割方案?(应用上述结论,写出解答过程)
【答案】见解析
【解析】探究四:用七边形的对角线把七边形分割成5个三角形,如图所示:
不妨把分割方案分成五类:
第1类:如图1,用A,G与B连接,先把七边形分割转化成1个三角形和1个六边形,由探究三知,有P6种不同的分割方案,所以,此类共有P6种不同的分割方案.
第2类:如图2,用A,G与C连接,先把七边形分割转化成2个三角形和1个五边形.由探究二知,有P5种不同的分割方案.所以,此类共有P5种分割方案.
第3类:如图3,用A,G与D连接,先把七边形分割转化成1个三角形和2个四边形.由探究一知,有2P4种不同的分割方案.所以,此类共有2P4种分割方案.
第4类:如图4,用A,G与E连接,先把七边形分割转化成2个三角形和1个五边形.由探究二知,有P5种不同的分割方案.所以,此类共有P5种分割方案.
第5类:如图5,用A,G与F连接,先把七边形分割转化成1个三角形和1个六边形.由探究三知,有P6种不同的分割方案.所以,此类共有P6种分割方案.
所以,P7=P6+P5+2P4+P5+P6=2P6+2×P6+2×P6==3P6=42(种).
故答案为:3,42;
【结论】:
由题意知:P5=×P4,P6=P5,P7=,…
∴Pn=Pn﹣1;
【应用】
根据结论得:P8=×P7==132.
P9=×P8==429.
则用九边形的对角线把九边形分割成7个三角形,共有429种不同的分割方案.
21.(9分)如图,已知OE是∠AOC的角平分线,OD是∠BOC的角平分线.
(1)若∠AOC=120°,∠BOC=30°,求∠DOE的度数;
(2)若∠AOB=90°,∠BOC=α,求∠DOE的度数.
【答案】见解析
【解析】(1)∵OE是∠AOC的角平分线,OD是∠BOC的角平分线,∠AOC=120°,∠BOC=30°,
∴∠EOC=60°,∠DOC=15°,
∴∠DOE=∠EOC﹣∠DOC=60°﹣15°=45°;
(2)∵OE是∠AOC的角平分线,OD是∠BOC的角平分线,∠AOB=90°,∠BOC=α,
∴∠EOC=(90°+α),∠DOC=α,
∴∠DOE=∠EOC﹣∠DOC=(90°+α)﹣α=45°.
22.(10分)A、B两地相距15千米,甲汽车在前边以50千米/小时从A出发,乙汽车在后边以40千米/小时从B出发,两车同时出发同向而行(沿BA方向),问经过几小时,两车相距30千米?
【答案】见解析
【解析】设经过x小时,两车相距30千米
由题意得:50x+15﹣40x=30
解得:x=1.5.
答:经过1.5小时,两车相距30千米
2021-2022学年九年级上学期北师大版期末数学模拟卷二(word版 含答案): 这是一份2021-2022学年九年级上学期北师大版期末数学模拟卷二(word版 含答案),共19页。试卷主要包含了选择题,填空题等内容,欢迎下载使用。
期末复习训练卷 2021-2022学年北师大版七年级上册数学(word版 含答案): 这是一份期末复习训练卷 2021-2022学年北师大版七年级上册数学(word版 含答案),共7页。试卷主要包含了选择题等内容,欢迎下载使用。
2021-2022学年北师大版数学七年级上册期末复习题(word版 含答案): 这是一份2021-2022学年北师大版数学七年级上册期末复习题(word版 含答案),共16页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。












