高端精品高中数学二轮专题-三角函数图像与性质（带答案）教案

这是一份高端精品高中数学二轮专题-三角函数图像与性质（带答案）教案，共23页。
三角函数的图像与性质
知识梳理.三角函数的图像与性质
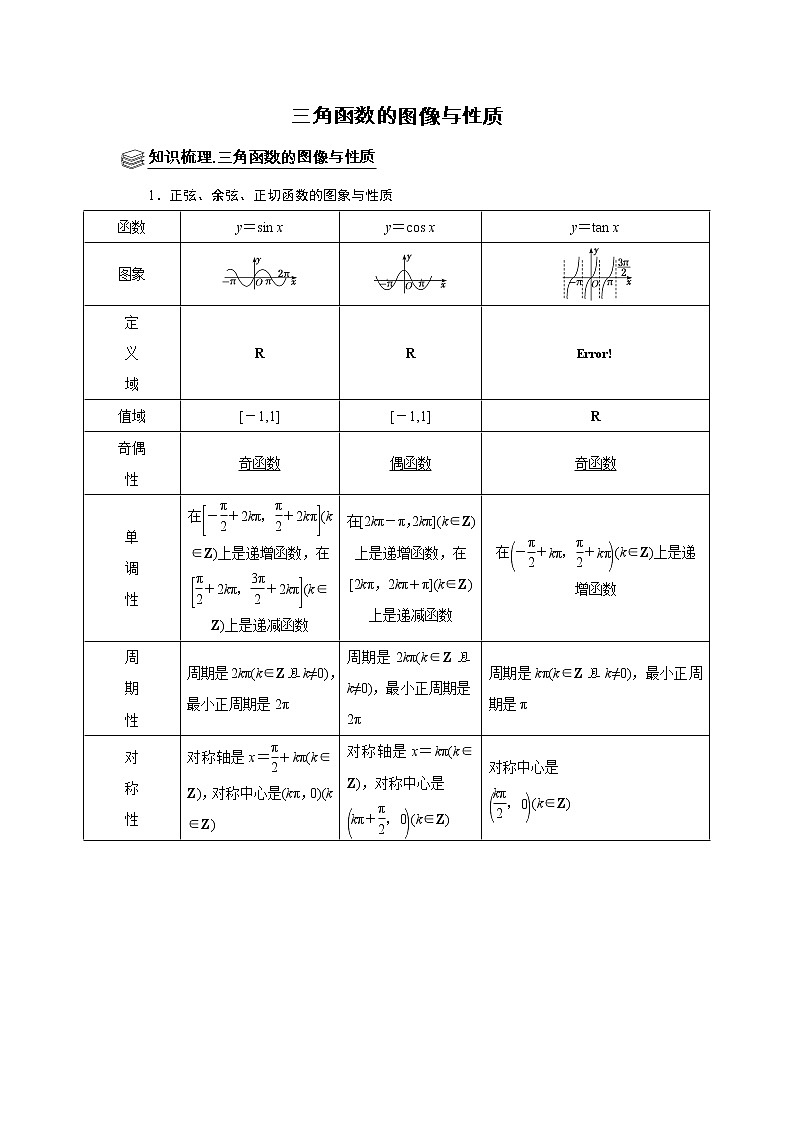
1．正弦、余弦、正切函数的图象与性质
函数
y＝sin x
y＝cos x
y＝tan x
图象



定
义
域
R
R

值域
[－1,1]
[－1,1]
R
奇偶
性
奇函数
偶函数
奇函数
单
调
性
在(k∈Z)上是递增函数，在(k∈Z)上是递减函数
在[2kπ－π，2kπ](k∈Z)上是递增函数，在[2kπ，2kπ＋π](k∈Z)上是递减函数
在(k∈Z)上是递增函数　　　　
周
期
性
周期是2kπ(k∈Z且k≠0)，最小正周期是2π
周期是2kπ(k∈Z且k≠0)，最小正周期是2π
周期是kπ(k∈Z且k≠0)，最小正周期是π
对
称
性
对称轴是x＝＋kπ(k∈Z)，对称中心是(kπ，0)(k∈Z)
对称轴是x＝kπ(k∈Z)，对称中心是
(k∈Z)
对称中心是
(k∈Z)




题型一. 三角函数图像的伸缩变换
1．要得到函数y＝3sin（2x+π3）的图象，只需要将函数y＝3cos2x的图象（　　）
A．向右平行移动π12个单位 B．向左平行移动π12个单位
C．向右平行移动π6个单位 D．向左平行移动π6个单位
【解答】解：函数y＝3sin（2x+π3）＝3cos[π2−（2x+π3）]＝3cos（π6−2x）＝3cos（2x−π6）＝3cos2（x−π12），
故把函数y＝3cos2x的图象向右平行移动π12个单位，可得函数y＝3sin（2x+π3）的图象，
故选：A．
2．已知曲线C1：y＝cosx，C2：y＝sin（2x+2π3），则下面结论正确的是（　　）
A．把C1上各点的横坐标伸长到原来的2倍，纵坐标不变，再把得到的曲线向右平移π6个单位长度，得到曲线C2
B．把C1上各点的横坐标伸长到原来的2倍，纵坐标不变，再把得到的曲线向左平移π12个单位长度，得到曲线C2
C．把C1上各点的横坐标缩短到原来的12，纵坐标不变，再把得到的曲线向右平移π6个单位长度，得到曲线C2
D．把C1上各点的横坐标缩短到原来的12，纵坐标不变，再把得到的曲线向左平移π12个单位长度，得到曲线C2
【解答】解：曲线C2：y＝sin（2x+2π3）＝cos（2x+π6），
把C1：y＝cosx上各点的横坐标缩短到原来的12，纵坐标不变，可得y＝cos2x的图象；
再把得到的曲线向左平移π12个单位长度，可以得到曲线C2：y＝cos（2x+π6）＝sin（2x+2π3）的图象，
故选：D．
3．函数y＝cos（2x+φ）的图象向右平移π2个单位长度后与函数y＝sin（2x+2π3）的图象重合，则|φ|的最小值为　5π6　．
【解答】解：函数y＝cos（2x+φ）的图象向右平移π2个单位长度后得到f（x）＝cos（2x﹣π+φ）＝﹣cos（2x+φ）＝sin（2x+φ+3π2）
由于与函数y＝sin（2x+2π3）的图象重合，
所以φ+3π2=2kπ+π3，
整理得：φ＝2kπ−7π6，
所以|φ|的最小值为5π6．
故答案为：5π6．
4．将函数f(x)=sin(ωx+φ)，(ω＞0，−π2＜φ＜π2)图象上每一点的横坐标缩短为原来的一半，纵坐标不变，再向右平移π4个单位长度得到y＝sinx的图象，则f(π6)=　32　．
【解答】解：将函数f(x)=sin(ωx+φ)，(ω＞0，−π2＜φ＜π2)图象上每一点的横坐标缩短为原来的一半，
纵坐标不变，可得y＝sin（2ωx+φ）的图象；
再把图象向右平移π4个单位长度得到y＝sin[2ω（x−π4）+φ]＝sin（2ωx−ωπ2+φ）的图象．
再根据所得图象为 y＝sinx，∴2ω=1−ωπ2+φ=0，求得ω=12，且 φ=π4，
∴f（x）＝sin（12x+π4），
则f(π6)=sin（π12+π4）＝sinπ3=32．
5．将函数f（x）＝sin2x的图象向右平移φ（0＜φ＜π2）个单位后得到函数g（x）的图象．若对满足|f（x1）﹣g（x2）|＝2的x1、x2，有|x1﹣x2|min=π3，则φ＝（　　）
A．5π12 B．π3 C．π4 D．π6
【解答】解：因为将函数f（x）＝sin2x的周期为π，函数的图象向右平移φ（0＜φ＜π2）个单位后得到函数g（x）的图象．若对满足|f（x1）﹣g（x2）|＝2的可知，两个函数的最大值与最小值的差为2，有|x1﹣x2|min=π3，
不妨x1=π4，x2=7π12，即g（x）在x2=7π12，取得最小值，sin（2×7π12−2φ）＝﹣1，此时φ=−π6，不合题意，
x1=3π4，x2=5π12，即g（x）在x2=5π12，取得最大值，sin（2×5π12−2φ）＝1，此时φ=π6，满足题意．
另解：f（x）＝sin2x，g（x）＝sin（2x﹣2φ），设2x1＝2kπ+π2，k∈Z，2x2﹣2φ=−π2+2mπ，m∈Z，
x1﹣x2=π2−φ+（k﹣m）π，
由|x1﹣x2|min=π3，可得π2−φ=π3，解得φ=π6，
故选：D．

题型二. 已知图像求解析式
1．下图是函数y＝Asin（ωx+φ）（x∈R）在区间[−π6，5π6]上的图象，为了得到这个函数的图象，只要将y＝sinx（x∈R）的图象上所有的点（　　）

A．向左平移π3个单位长度，再把所得各点的横坐标缩短到原来的12，纵坐标不变
B．向左平移π3个单位长度，再把所得各点的横坐标伸长到原来的2倍，纵坐标不变
C．向左平移π6个单位长度，再把所得各点的横坐标缩短到原来的12，纵坐标不变
D．向左平移π6个单位长度，再把所得各点的横坐标伸长到原来的2倍，纵坐标不变
【解答】解：由图象可知函数的周期为π，振幅为1，
所以函数的表达式可以是y＝sin（2x+φ）．
代入（−π6，0）可得φ的一个值为 π3，
故图象中函数的一个表达式是y＝sin（2x+π3），
即y＝sin2（x+π6），
所以只需将y＝sinx（x∈R）的图象上所有的点向左平移 π3个单位长度，再把所得各点的横坐标缩短到原来的 12倍，纵坐标不变．
故选：A．
2．已知函数y=sin(ωx+φ)(ω＞0，|φ|＜π2)的部分图象如图所示，则（　　）

A．ω=π2，φ=−π4 B．ω=π2，φ=π4 C．ω=π，φ=−π4 D．ω=π，φ=π4
【解答】解：结合图象52−32=1，是14个周期，
故T＝4，
故ω=2π4=π2，
而y＝sin（π2×32+φ）＝1，解得：φ=−π4，
故选：A．
3．已知函数f（x）＝Acos（ωx+φ）的图象如图所示，f（π2）=−23，则f（0）＝（　　）

A．−23 B．−12 C．23 D．12
【解答】解：由题意可知，此函数的周期T＝2（1112π−712π）=2π3，
故2πω=2π3，∴ω＝3，f（x）＝Acos（3x+φ）．
f（π2）＝Acos（3π2+φ）＝Asinφ=−23．
又由题图可知f（7π12）＝Acos（3×7π12+φ）＝Acos（φ−14π）
=22（Acosφ+Asinφ）＝0，
∴f（0）＝Acosφ=23．
故选：C．
4．已知函数f（x）＝Atan（ωx+φ）（ω＞0，|φ|＜π2）的部分图象如图所示，下列关于函数g（x）＝Acos（ωx+φ）（x∈R）的表述正确的是（　　）

A．函数g（x）的图象关于点（π4，0）对称
B．函数g（x）在[−π8，3π8]递减
C．函数g（x）的图象关于直线x=π8对称
D．函数h（x）＝cos2x的图象上所有点向左平移π4个单位得到函数g（x）的图象
【解答】解：根据函数f（x）＝Atan（ωx+φ）（ω＞0，|φ|＜π2）的部分图象知，
最小正周期为T＝2×（3π8−π8）=π2，∴ω=πT=2；
又ω•π8+φ=π2+kπ，k∈Z，
φ=π4+kπ，k∈Z；
∴φ=π4，
∴f（0）＝Atanπ4=A＝1，
∴函数g（x）＝cos（2x+π4）；
x=π4时，g（π4）＝cos（π2+π4）=−22≠0，
g（x）的图象不关于点（π4，0）对称，A错误；
x∈[−π8，3π8]时，2x+π4∈[0，π]，
g（x）在[−π8，3π8]上单调递减，B正确；
x=π8时，g（π8）＝cos（π4+π4）＝0，
g（x）的图象不关于直线x=π8对称，C错误；
h（x）＝cos2x的图象上所有点向左平移π4个单位，
得h（x+π4）＝cos2（x+π4）＝cos（2x+π2）的图象，
不是函数g（x）的图象，D错误．
故选：B．

题型三. 三角函数的性质
考点1.单调性
1．函数y＝sin（﹣2x+π3）的单调递减区间是（　　）
A．[kπ−π12，kπ+5π12]，k∈Z B．[2kπ−π12，2kπ+5π12]，k∈Z
C．[kπ−π6，kπ+5π6]，k∈Z D．[2kπ−π6，2kπ+5π6]，k∈Z
【解答】解：∵函数y＝sin（﹣2x+π3）＝﹣sin（2x−π3），故本题即求函数y＝sin（2x−π3） 的增区间．
令2kπ−π2≤2x−π3≤2kπ+π2，k∈z，求得kπ−π12≤x≤kπ+5π12，k∈Z，故函数y＝sin（2x−π3） 的增区间为[kπ−π12，kπ+5π12]，k∈Z，
故选：A．
2．已知函数f(x)=Asin(x+φ)(A＞0，−π2＜φ＜0)在x=5π6时取得最大值，则f（x）在[﹣π，0]上的单调增区间是（　　）
A．[−π，−5π6] B．[−5π6，−π6] C．[−π3，0] D．[−π6，0]
【解答】解：因为函数f（x）＝Asin（x+φ）（A＞0）在x=5π6取最大值
所以可得，Asin(5π6+φ)=A⇒sin（5π6+φ）＝1
又因为−π2＜φ＜0 所以 φ=−π3
而f(x)=Asin(x−π3)（A＞0）与y＝sin（x−π3）的单调性相同且[﹣π，0]
故函数在[−π6，0]上单调递增，在[﹣π，−π6]上单调递减
故选：D．
3．已知函数f（x）＝sin（2x+π3）在区间[0，a]（其中a＞0）上单调递增，则实数a的取值范围是（　　）
A．{a|0＜a≤π12} B．{a|0＜a≤π2}
C．{a|a＝kπ+π12，k∈N*} D．{a|2kπ＜a≤2kπ+π12，k∈N*}
【解答】解：由−π2+2kπ≤2x+π3≤π2+2kπ，
得−5π12+kπ≤x≤π12+kπ，k∈Z．
取k＝0，得−5π12≤x≤π12，
则函数数f（x）＝sin（2x+π3）的一个增区间为[−5π12，π12]．
∵函数f（x）＝sin（2x+π3）在区间[0，a]（其中a＞0）上单调递增，
∴0＜a≤π12．
故选：A．
4．已知ω＞0，函数f（x）＝sin（ωx+π4）在区间（π2，π）上单调递减，则实数ω的取值范围是（　　）
A．[12，54] B．[12，34] C．(0，12] D．（0，2]
【解答】解：法一：令：ω=2⇒(ωx+π4)∈[5π4，9π4]不合题意 排除（D）
ω=1⇒(ωx+π4)∈[3π4，5π4]合题意 排除（B）（C）
法二：ω(π−π2)≤π⇔ω≤2，(ωx+π4)∈[π2ω+π4，πω+π4]⊂[π2，3π2]
得：π2ω+π4≥π2，πω+π4≤3π2⇔12≤ω≤54．
故选：A．



考点2.周期性、奇偶性、对称性
1．已知函数f（x）＝cos2x+sin2（x+π6），则（　　）
A．f（x）的最小正周期为π，最小值为12
B．f（x）的最小正周期为π，最小值为−12
C．f（x）的最小正周期为2π，最小值为12
D．f（x）的最小正周期为2π，最小值为−12
【解答】解：∵函数f（x）＝cos2x+sin2（x+π6）=1+cos2x2+1−cos(2x+π3)2=1+12cos2x−12cos（2x+π3）＝1+12•12cos2x+34sin2x＝1+12cos（2x−π3），
故函数f（x）的最小正周期为2π2=π，最小值为1−12=12，
故选：A．
2．已知f（x）＝sin2x+|sin2x|（x∈R），则下列判断正确的是（　　）
A．f（x）是周期为2π的奇函数
B．f（x）是值域为[0，2]周期为π的函数
C．f（x）是周期为2π的偶函数
D．f（x）是值域为[0，1]周期为π的函数
【解答】解：若2kπ≤2x≤2kπ+π，即kπ≤x≤kπ+π2时，sin2x≥0，
f（x）＝sin2x+|sin2x|＝2sin2x；
若2kπ+π≤2x≤2kπ+2π，即kπ+π2≤x≤kπ+π时，sin2x＜0，
f（x）＝sin2x+|sin2x|＝0，
作出函数图象，如下图：

根据图象可知f（x）为周期函数，最小正周期为π，
函数的值域为[0，2]．
故选：B．
3．将函数y＝sin2x−3cos2x的图象沿x轴向右平移a个单位（a＞0）所得图象关于y轴对称，则a的最小值是（　　）
A．712π B．π4 C．π12 D．π6
【解答】解：将函数y＝sin2x−3cos2x的图象沿x轴向右平移a个单位（a＞0），
得到的函数：y＝sin2（x﹣a）−3cos2（x﹣a）＝sin（2x﹣2a）−3cos（2x﹣2a）
＝2sin（2x﹣2a−π3），
∵所得图象关于y轴对称，
∴2a+π3=π2+kπ（k∈z），解得a=π12+kπ2（k∈z），
∴a的最小值是π12．
故选：C．
4．已知函数f（x）＝asinx﹣bcosx（ab≠0，x∈R）在x=π4处取得最大值，则函数y＝f（π4−x）是（　　）
A．偶函数且它的图象关于点（π，0）对称
B．偶函数且它的图象关于点(3π2，0)对称
C．奇函数且它的图象关于点(3π2，0)对称
D．奇函数且它的图象关于点 （π，0）对称
【解答】解：将已知函数变形f（x）＝asinx﹣bcosx=a2+b2sin（x﹣φ），其中tanφ=ba．
又f（x）＝asinx﹣bcosx在x=π4处取得最大值，
∴π4−φ=π2+2kπ（k∈Z）得φ=−π4−2kπ（k∈Z），
∴f（x）=a2+b2sin（x+π4），
∴函数y=f(π4−x)=a2+b2sin（π2−x）=a2+b2cosx，
∴函数是偶函数且它的图象关于点(3π2，0)对称．
故选：B．


考点3.三角函数性质综合
1．已知函数f（x）＝Asin（ωx+φ）（A＞0，ω＞0，|φ|＜π）是奇函数，将y＝f（x）的图象上所有点的横坐标伸长到原来的2倍（纵坐标不变），所得图象对应的函数为g（x）．若g（x）的最小正周期为2π，且g（π4）=2，则f（3π8）＝（　　）
A．﹣2 B．−2 C．2 D．2
【解答】解：∵f（x）是奇函数，∴φ＝0，
则f（x）＝Asin（ωx）
将y＝f（x）的图象上所有点的横坐标伸长到原来的2倍（纵坐标不变），所得图象对应的函数为g（x）．
即g（x）＝Asin（12ωx）
∵g（x）的最小正周期为2π，
∴2π12ω=2π，得ω＝2，
则g（x）＝Asinx，f（x）＝Asin2x，
若g（π4）=2，则g（π4）＝Asinπ4=22A=2，即A＝2，
则f（x）＝2sin2x，则f（3π8）＝2sin（2×3π8=2sin3π4=2×22=2，
故选：C．
2．已知函数f（x）＝sinωx+cosωx（ω＞0），x∈R，若函数f（x）在区间（﹣ω，ω）内单调递增，且函数y＝f（x）的图象关于直线x＝ω对称，则ω的值为　π2　．
【解答】解：∵f（x）＝sinωx+cosωx=2sin（ωx+π4），
∵函数f（x）在区间（﹣ω，ω）内单调递增，ω＞0
∴2kπ−π2≤ωx+π4≤2kπ+π2，k∈Z可解得函数f（x）的单调递增区间为：[2kπ−3π4ω，2kπ+π4ω]，k∈Z，
∴可得：﹣ω≥2kπ−3π4ω①，ω≤2kπ+π4ω②，k∈Z，
∴解得：0＜ω2≤3π4−2kπ且0＜ω2≤2kπ+π4，k∈Z，
解得：−18＜k＜38，k∈Z，
∴可解得：k＝0，
又∵由ωx+π4=kπ+π2，可解得函数f（x）的对称轴为：x=kπ+π4ω，k∈Z，
∴由函数y＝f（x）的图象关于直线x＝ω对称，可得：ω2=π4，可解得：ω=π2．
故答案为：π2．
3．若函数f（x）＝cos2x+asinx在区间（π6，π2）是减函数，则a的取值范围是　（﹣∞，2]　．
【解答】解：由f（x）＝cos2x+asinx
＝﹣2sin2x+asinx+1，
令t＝sinx，
则原函数化为y＝﹣2t2+at+1．
∵x∈（π6，π2）时f（x）为减函数，
则y＝﹣2t2+at+1在t∈（12，1）上为减函数，
∵y＝﹣2t2+at+1的图象开口向下，且对称轴方程为t=a4．
∴a4≤12，解得：a≤2．
∴a的取值范围是（﹣∞，2]．
故答案为：（﹣∞，2]．
4．若函数f（x）＝x−13sin2x+asinx在（﹣∞，+∞）单调递增，则a的取值范围是（　　）
A．[﹣1，1] B．[﹣1，13] C．[−13，13] D．[﹣1，−13]
【解答】解：函数f（x）＝x−13sin2x+asinx的导数为f′（x）＝1−23cos2x+acosx，
由题意可得f′（x）≥0恒成立，
即为1−23cos2x+acosx≥0，
即有53−43cos2x+acosx≥0，
设t＝cosx（﹣1≤t≤1），即有5﹣4t2+3at≥0，
当t＝0时，不等式显然成立；
当0＜t≤1时，3a≥4t−5t，
由4t−5t在（0，1]递增，可得t＝1时，取得最大值﹣1，
可得3a≥﹣1，即a≥−13；
当﹣1≤t＜0时，3a≤4t−5t，
由4t−5t在[﹣1，0）递增，可得t＝﹣1时，取得最小值1，
可得3a≤1，即a≤13．
综上可得a的范围是[−13，13]．
另解：设t＝cosx（﹣1≤t≤1），即有5﹣4t2+3at≥0，
由题意可得5﹣4+3a≥0，且5﹣4﹣3a≥0，
解得a的范围是[−13，13]．
故选：C．
5．已知函数f（x）＝sin（ωx+π6），其中ω＞0，若f（π6）＝f（π3），且f（x）在区间（π6，π3）上有最小值、无最大值，则ω等于（　　）
A．403 B．283 C．163 D．43
【解答】解：对于函数f（x）＝sin（ωx+π6），由f（π6）＝f（π3），可得函数的图象关于直线x=π6+π32=π4 对称，
再根据f（x）在区间（π6，π3）上有最小值、无最大值，可得ω•π4+π6=3π2，求得ω=163，
故选：C．
6．设函数f（x）＝Asin（ωx+φ）（A，ω，φ是常数，A＞0，ω＞0）若f（x）在区间[π6，π2]上具有单调性，且f（π2）＝f（2π3）＝﹣f（π6），则f（x）的最小正周期为　π　．
【解答】解：由f（π2）＝f（2π3），可知函数f（x）的一条对称轴为x=π2+2π32=7π12，
则x=π2离最近对称轴距离为7π12−π2=π12．
又f（π2）＝﹣f（π6），则f（x）有对称中心（π3，0），
由于f（x）在区间[π6，π2]上具有单调性，
则π2−π6≤12T⇒T≥2π3，从而7π12−π3=T4⇒T＝π．
故答案为：π．

题型四. 三角函数最值
1．函数f（x）=15sin（x+π3）+cos（x−π6）的最大值为（　　）
A．65 B．1 C．35 D．15
【解答】解：函数f（x）=15sin（x+π3）+cos（x−π6）=15sin（x+π3）+cos（﹣x+π6）=15sin（x+π3）+sin（x+π3）
=65sin（x+π3）≤65．
故选：A．
2．函数f（x）＝cos（ωx+π3）（ω＞0）在[0，π]内的值域为[﹣1，12]，则ω的取值范围为（　　）
A．[32，53] B．[23，43] C．[23，+∞) D．[23，32]
【解答】解：函数f（x）＝cos（ωx+π3）（ω＞0），
当x∈[0，π]时，f（x）∈[﹣1，12]，
∴﹣1≤cos（ωx+π3）≤12，结合余弦函数的性质，
则π≤ωπ+π3≤5π3，
解得23≤ω≤43，
∴ω的取值范围是[23，43]．
故选：B．
3．已知函数f（x）＝cos2x+sinx，则下列说法中正确的是（　　）
A．f（x）的一条对称轴为x=π4
B．f（x）在（π6，π2）上是单调递减函数
C．f（x）的对称中心为（π2，0）
D．f（x）的最大值为1
【解答】解：对于A，f（π2−x）＝cos2（π2−x）+sin（π2−x）
＝cos（π﹣2x）+cosx＝﹣cos2x+cosx≠f（x），
所以x=π4不是f（x）的对称轴，故A错误；
对于B，f′（x）＝﹣2sin2x+cosx＝﹣4sinxcosx+cosx＝cosx（1﹣4sinx），
当x∈（π6，π2）时，cosx＞0，12＜sinx＜1，所以﹣3＜1﹣4sinx＜﹣1，
所以f′（x）＜0，f（x）单调递减，故B正确；
对于C，f（π﹣x）+f（x）＝cos2（π﹣x）+sin（π﹣x）+cos2x+sinx
＝2cos2x+2sinx＝2f（x）≠0，
所以（π2，0）不是f（x）的对称中心，故C错误；
对于D，f（x）＝cos2x+sinx＝1﹣2sin2x+sinx，
令t＝sinx∈[﹣1，1]，则y＝﹣2t2+t+1，
当t=14时，函数取得最大值为﹣2×(14)2+14+1=98，
所以f（x）的最大值为98，故D错误．
故选：B．
4．若0＜x≤π3，则函数y＝sinx+cosx+sinxcosx的值域为　（1，12+2]　．
【解答】解：令sinx+cosx＝t，则sinxcosx=t2−12，
∴y＝sinxcosx+sinx+cosx＝t+t2−12=12t2+t−12=12（t+1）2﹣1．
∵x∈（0，π3]，t＝sinx+cosx=2sin（x+π4）∈（1，2]．
∴ymax=12+2，
x＝0时，y＝1．
函数y＝sinx+cosx+sinxcosx的值域为：（1，12+2]．
5．已知函数f(x)=2sinωx⋅cos2(ωx2−π4)−sin2ωx(ω＞0)在区间[−2π5，5π6]上是增函数，且在区间[0，π]上恰好取得一次最大值1，则ω的取值范围是（　　）
A．(0，35] B．[12，35] C．[12，34] D．[12，52)
【解答】解：由f(x)=2sinωx⋅cos2(ωx2−π4)−sin2ωx(ω＞0)，
化简，f（x）＝sinωx（1+sinωx）﹣sin2ωx＝sinωx，
由ωx=π2+2kπ，k∈z，即x=π2ω+2kπω=π2ω(1+4k)时，取得最大值1，
因为x∈[0，π]上恰好取得一次最大值，所以k＝0，π2ω∈[0，π]，
所以ω≥12，
f（x）在区间[−2π5，5π6]上是增函数，根据题意
π2ω≥5π6，即ω≤35，
结合上面所述，ω∈[12，35]，
故选：B．
6．已知函数f（x）＝cosx•sin（x+π3）−3cos2x+34，x∈R
（1）求f（x）的最小正周期；
（2）求f（x）在闭区间[0，π2]上的最大值和最小值及相应的x值；（3）若不等式|f（x）﹣m|＜2在x∈[0，π2]上恒成立，求实数m的取值范围．
【解答】解：（1）由已知，有：f（x）＝cosx•（12sinx+32cosx）−3cos2x+34=12sinx⋅cosx−32cos2x+34=14sin2x−34cos2x=12sin（2x−π3），﹣﹣﹣﹣﹣（3分）
所以f（x）的最小正周期T=2π2=π．﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣（4分）
（2）∵x∈[0，π2]，∴2x−π3∈[−π3，2π3]
∴f（x）min＝f（0）=−34，f（x）max＝f（5π12）=12．﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣（8分）
（3）∵x∈[0，π2]，∴−π3≤2x−π3≤2π3，
∴−34≤12sin（2x−π3）≤12，
∴f（x）max=12，f（x）min=−34
∵不等式|f（x）﹣m|＜2⇔f（x）﹣2＜m＜f（x）+2
∴|f（x）﹣m|＜2在x∈[0，π2]上恒成立⇔m＞f（x）max﹣2且m＜f（x）min+2
∴−32＜m＜2−34，即：m的取值范围是（−32，2−34），
m的取值范围（−32，2−34）﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣（12分）

题型五.三角函数零点
1．已知函数f（x）＝sinωx−3cosωx（ω＞0），若方程f（x）＝﹣1在（0，π）上有且只有四个实数根，则实数ω的取值范围为　72＜ω≤256　．
【解答】解：函数f（x）＝sinωx−3cosωx（ω＞0），
＝2sin（ωx−π3），
令2sin（ωx−π3）＝﹣1，
解得：ωx−π3=−π6+2kπ，或ωx−π3=7π6+2kπ（k∈Z），
所以：x=π6ω+2kπω或x=3π2ω+2kπω（k∈Z），
设直线y＝﹣1与y＝f（x）在（0，+∞）上从左到右的第四个交点为A第五个交点为B，
则：xA=3π2ω+2πω，xB=π6ω+4πω．
由于方程f（x）＝﹣1在（0，π）上有且只有四个实数根，
则：xA＜π≤xB，
即：3π2ω+2πω＜π≤π6ω+4πω，
解得：72＜ω≤256．
故答案为：72＜ω≤256．
2．已知函数f（x）=3sinωxcosωx+cos2ωx−12，（ω＞0，x∈R），若函数f（x）在区间（π2，π）内没有零点，则ω的取值范围（　　）
A．（0，512] B．（0，512]∪[56，1112]
C．（0，58] D．（0，56]∪[1112，1）
【解答】解：函数f（x）=3sinωcosωx+cos2ωx−12，
=32sin2ωx+1+cos2ωx2−12，
=sin(2ωx+π6)，
函数f（x）在区间（π2，π）内没有零点，
所以：f(π2)⋅f(π)＞0，
即：sin(πω+π6)⋅sin(2ωπ+π6)＞0，
所以：①sin(πω+π6)＞0sin(2ωπ+π6)＞0，
解得：ω∈(0，512]，
②sin(πω+π6)＜0sin(2ωπ+π6)＜0，
解得：ω∈[56，1112]，
综上所述：ω∈（0，512]∪[56，1112]，
故选：B．
3．函数f(x)=2sin(2ωx+π6)(ω＞0)图象上有两点A（s，t），B（s+2π，t）（﹣2＜t＜2），若对任意s∈R，线段AB与函数图象都有五个不同交点，若f（x）在[x1，x2]和[x3，x4]上单调递增，在[x2，x3]上单调递减，且x4−x3=x2−x1=23(x3−x2)，则x1的所有可能值是　−π6+kπ，k∈Z　
【解答】解：由于|AB|＝2π且线段AB与函数图象都有五个不同交点，
则2T＝2×2π2ω=2π，即ω＝1，
则f（x）＝2sin（2x+π6），
由题意得x3﹣x2=T2=π2，
则x4−x3=x2−x1=23(x3−x2)=23×π2=π3，
即x1＝x2−π3，
∵若f（x）在[x1，x2]和[x3，x4]上单调递增，在[x2，x3]上单调递减，
∴f（x）在x2处取得最大值，即f（x2）＝2sin（2x2+π6）＝2，
即sin（2x2+π6）＝1，则2x2+π6=2kπ+π2，
得x2＝kπ+π6，
则x1＝x2−π3=kπ+π6−π3=kπ−π6，k∈Z，
故答案为：x1＝kπ−π6，k∈Z．


课后作业. 三角函数的图像与性质
1．函数f（x）＝Asin（ωx+φ）（A＞0，ω＞0，﹣π＜φ＜0）的部分图象如图所示，为了得到g（x）＝Asinωx的图象，只需将函数y＝f（x）的图象（　　）

A．向左平移π3个单位长度
B．向左平移π12个单位长度
C．向右平移π3个单位长度
D．向右平移π12个单位长度
【解答】解：根据函数f（x）＝Asin（ωx+φ）（A＞0，ω＞0，﹣π＜φ＜0）的部分图象，可得A＝2，
12⋅2πω=π3+π6，∴ω＝2．
再根据五点法作图可得2×π3+φ=π2，求得φ=−π6，∴f（x）＝2sin（2x−π6）．
为了得到g（x）＝Asinωx＝2sin2x的图象，
只需将函数y＝f（x）＝2sin（2x−π6）的图象向左平移π12个单位长度，
故选：B．
2．关于函数y＝2sin（3x+π4）+1，下列叙述正确的是（　　）
A．其图象关于直线x=−π4对称
B．其图象关于点（π12，1）对称
C．其值域是[﹣1，3]
D．其图象可由y＝2sin（x+π4）+1图象上所有点的横坐标变为原来的13得到
【解答】解：因为sin[3×(−π4)+π4]＝﹣1，y取得最小值，故x=−π4是对称轴，故A正确；
因为sin(3×π12+π4)=1≠0，故(π12，1)不是对称中心，故B错误；
因为sin（3x+π4）∈[﹣1，1]，故2sin（3x+π4）+1∈[﹣1，3]，故C正确；
由y＝2sin（x+π4）+1到y＝2sin（3x+π4）+1系数中，只有x的系数变成了原来的3倍，故所有点的横坐标变成原来的13，故D正确．
故选：ACD．
3．已知函数f（x）＝（12a−3）sinx+（32a+1）cosx，将f（x）的图象向右平移π3个单位长度得到函数g（x）的图象，若对任意x∈R，都有g（x）≤g（π4），则a的值为　2　．
【解答】解：f（x）＝（12a−3）sinx+（32a+1）cosx＝asin（x+π3）﹣2sin（x−π6），将f（x）的图象向右平移π3个单位长度得到函数g（x）＝asinx﹣2sin（x−π2）＝asinx+2cosx，
因为对任意x∈R，都有g（x）≤g（π4），所以a2+4=22a+2，解得a＝2；
故答案为：2．
4．已知函数f（x）＝sin（ωx+φ）（ω＞1，0≤φ≤π）是R上的偶函数，其图象关于点M（3π4，0）对称，且在区间[0，π2]上是单调函数，则ω和φ的值分别为（　　）
A．23，π4 B．2，π3 C．2，π2 D．103，π2
【解答】解：由f（x）是偶函数，φ＝kπ+π2，
∵0≤φ≤π，∴当k＝0时，φ=π2，
∴f（x）＝sin（ωx+π2）＝cosωx，
∵f（x）图象上的点关于M（3π4，0）对称，
∴f（3π4）＝cos3π4ω＝0，故3π4ω＝kπ+π2，k∈Z，
即ω=23（2k+1），
∵f（x）在区间[0，π2]上是单调函数，可得π2≤12⋅2πω=πω，即ω≤2
又∵ω=23（2k+1），ω＞1
∴当k＝1时可得ω＝2．
故选：C．
5．已知函数f（x）＝sin（ωx+φ），其中ω＞0，|φ|≤π2，−π4为f（x）的零点：且f（x）≤|f（π4）|恒成立，f（x）在区间（−π12，π24）上有最小值无最大值，则ω的最大值是（　　）
A．11 B．13 C．15 D．17
【解答】解：由题意知函数f（x）＝sin（ωx+φ）（ω＞0，|φ|≤π2），
x=π4 为y＝f（x）图象的对称轴，x=−π4为f（x）的零点，
∴2n−14•2πω=π2，n∈N*，∴ω＝2n+1，n∈N*，
f（x）在区间（−π12，π24）上有最小值无最大值，
∴周期T≥（π24+π12）=π8，即2πω≥π8，∴ω≤16．
∴要求ω的最大值，结合选项，先检验ω＝15，
当ω＝15时，由题意可得−π4×15+φ＝kπ，φ=−π4，函数为y＝f（x）＝sin（15x−π4），
在区间（−π12，π24）上，15x−π4∈（−3π2，3π8），
此时f（x）在15x−π4=−π2时取得最小值，∴ω＝15满足题意．
则ω的最大值为15，
故选：C．
6．已知函数f（x）＝2sin（ωx−π6）sin（ωx+π3）（ω＞0），若函数g（x）＝f（x）+32在[0，π2]上有且只有三个零点，则ω的取值范围为（　　）
A．[2，113） B．（2，113） C．[73，103） D．（73，103）
【解答】解：f（x）＝2sin（ωx−π6）sin（ωx+π3）＝2sin（ωx−π2+π3）sin（ωx+π3）
＝﹣2cos（ωx+π3）sin（ωx+π3）＝﹣sin（2ωx+2π3），
由g（x）＝f（x）+32=0得f（x）=−32，
即﹣sin（2ωx+2π3）=−32，
得sin（2ωx+2π3）=32，
∵0≤x≤π2，
∴0≤2ωx≤πω，则2π3≤2ωx+2π3≤πω+2π3，
∵sin2π3=32，
∴要使sin（2ωx+2π3）=32，在0≤x≤π2上有三个根，
∴2π3+2π≤ωπ+2π3＜π3+4π，
得2π≤ωπ＜11π3，即2≤ω＜113，
即ω的取值范围是[2，113），
故选：A．