

所属成套资源:高中数学二轮专题教案
高端精品高中数学二轮专题-任意角的三角函数(带答案)教案
展开这是一份高端精品高中数学二轮专题-任意角的三角函数(带答案)教案,共9页。
任意角的三角函数
知识梳理.任意角的三角函数
1.角的概念的推广
(1)定义:角可以看成平面内一条射线绕着端点从一个位置旋转到另一个位置所成的图形.
(2)分类
(3)终边相同的角:所有与角α终边相同的角,连同角α在内,可构成一个集合S={β|β=α+2kπ,k∈Z}.
2.弧度制的定义和公式
(1)定义:把长度等于半径长的弧所对的圆心角叫做1弧度的角,弧度记作rad.
(2)公式:
角α的弧度数公式 | |α|=(l表示弧长) |
角度与弧度的换算 | ①1°=rad;②1 rad=° |
弧长公式 | l=|α|r |
扇形面积公式 | S=lr=|α|r2 |
3.任意角的三角函数
(1)定义:设α是一个任意角,它的终边与单位圆交于点P(x,y),那么sin α=y,cos α=x,tan α=(x≠0).
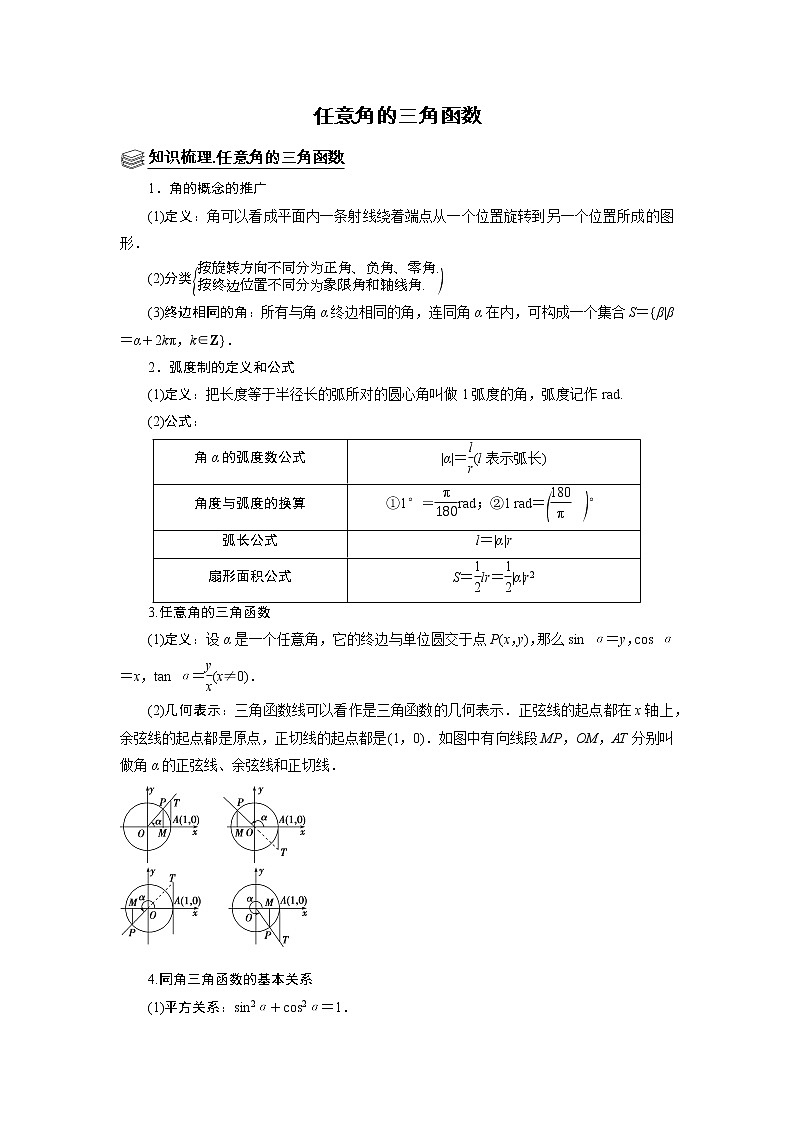
(2)几何表示:三角函数线可以看作是三角函数的几何表示.正弦线的起点都在x轴上,余弦线的起点都是原点,正切线的起点都是(1,0).如图中有向线段MP,OM,AT分别叫做角α的正弦线、余弦线和正切线.
4.同角三角函数的基本关系
(1)平方关系:sin2α+cos2α=1.
(2)商数关系:=tan_α(α≠+kπ,k∈Z).
5.三角函数的诱导公式
公式 | 一 | 二 | 三 | 四 | 五 | 六 |
角 | 2kπ+α (k∈Z) | π+α | -α | π-α | -α | +α |
正弦 | sin α | -sin_α | -sin_α | sin_α | cos_α | cos_α |
余弦 | cos_α | -cos_α | cos_α | -cos_α | sin_α | -sin_α |
正切 | tan α | tan_α | -tan_α | -tan_α |
|
|
口诀 | 函数名不变,符号看象限 | 函数名改变,符号看象限 | ||||
题型一. 同角之间的关系
1.已知角α的终边经过点P(1,m),且sinα,则cosα=( )
A.± B. C. D.
【解答】解:因为角a的终边经过点P(1,m),所以OP
因为sinα,所以:;
所以m=﹣3.(正值舍)
故cosα;
故选:C.
2.已知a是第二象限角,,则cosα=( )
A. B. C. D.
【解答】解:∵α为第二象限角,tanα,
∴cosα.
故选:B.
3.已知,,则sinα=( )
A. B. C. D.
【解答】解:∵,,
∴cosα,即cos2α,
又∵sin2α+cos2α=1,
∴sin2α1,即sin2α+sinα0,
解得sinα,负值舍去.
故选:C.
4.已知sinθ+cosθ(0<θ),则sinθ﹣cosθ的值为 .
【解答】解:∵sinθ+cosθ0,0<θ,
∴(sinθ+cosθ)2=sin2θ+cos2θ+2sinθcosθ=1+2sinθcosθ,sinθ﹣cosθ<0,
∴2sinθcosθ,
∴(sinθ﹣cosθ)2=sin2θ+cos2θ﹣2sinθcosθ=1﹣2sinθcosθ,
则sinθ﹣cosθ.
故答案为:.
题型二. 齐次式
1.已知tanα=2,则的值为( )
A.9 B.6 C.﹣2 D.﹣3
【解答】解:因为tanα=2,
则9.
故选:A.
2.已知tanα,则( )
A. B. C. D.
【解答】解:.
故选:B.
3.已知tanα=﹣1,则2sin2α﹣3cos2α=( )
A. B. C. D.
【解答】解:因为tanα=﹣1,
则2sin2α﹣3cos2α.
故选:B.
4.已知2cos2α﹣3sin2α=1,α∈(,﹣π),那么tanα的值为( )
A.2 B.﹣2 C. D.
【解答】解:因为2cos2α﹣3sin2α=2(1﹣sin2α)﹣3sin2α=1,
可得sin2α,cos2α,
因为α∈(,﹣π),
所以sinα,cosα,可得tanα.
故选:D.
题型三.
1.已知cosα﹣3sinα=0,则的值为( )
A. B. C. D.
【解答】解:因为cosα﹣3sinα=0,
所以cosα=3sinα,
则.
故选:C.
2.已知sinα+cosα,则sinα•cosα=( )
A. B. C. D.
【解答】解:已知sinα+cosα,
两边平方可得:sin2α+cos2α+2sinαcosα,整理得:1+2sinα•cosα,
解得:sinα•cosα.
故选:C.
3.已知,则( )
A.﹣6 B.﹣7 C.﹣8 D.﹣9
【解答】解:由得到:,
得,
所以.
故选:C.
4.若α∈(,π),2sinα+cosα,则tanα=( )
A.﹣2 B.2 C. D.
【解答】解:由2sinα+cosα,
两边平方,可得:(2sinα+cosα)2,即4sin2α+4sinαcosα+cos2α.
∴,
∴,则11tan2α+20tanα﹣4=0.
解得:tanα=﹣2或tanα.
∵α∈(,π),
∴tanα=﹣2.
故选:A.
题型四. 诱导公式
1.已知sin(π+α),则( )
A. B. C. D.
【解答】解:∵sin(π+α)sinα,∴sinα,
∴sinα,
故选:C.
2.已知sin(α),则cos(π+α)=( )
A. B. C. D.
【解答】解:∵,
∴cosα,
∴cos(π+α)=﹣cosα.
故选:A.
3.,则 .
【解答】解:∵αα=π,
∴α=π﹣(α),
即sin(α)=sin[π﹣(α)]=sin(α),
故答案为:.
4.已知,则 0 .
【解答】解:∵(θ)+(θ),
∴θ(θ),
∴cos(θ)+sin(θ)
=cos(θ)+sin[(θ)]
=cos(θ)﹣cos(θ)
=0.
故答案为:0.
课后作业.任意角的三角函数
1.已知角θ的终边上有一点P(﹣4a,3a)(a≠0),则2sinθ+cosθ的值是( )
A. B. C.或 D.不确定
【解答】解:角α的终边经过点P(﹣4a,3a),故|OP|5|a|;
由三角函数的定义知
当a>0时,sinα,cosα,得2sinα+cosα;
当a<0时,sinα,cosα,得2sinα+cosα.
故选:C.
2.已知tanA=2,则( )
A. B. C. D.
【解答】解:因为tanA=2,
所以.
故选:D.
3.已知A是三角形的内角,且sinA+cosA,则tanA等于 4 .
【解答】解:A是三角形的内角,sinA+cosA,又因为sin2A+cos2A=1,
所以2sinAcosA,A为锐角,
所以,
所以tan2A﹣8tanA+1=0,
所以tanA=4.
故答案为:4.
4.已知2sinθ﹣cosθ=1,则的值为( )
A. B.0 C.2 D.0或2
【解答】解:由题意可得2sinθ﹣1=cosθ,
两边同时平方可得,4sin2θ﹣4sinθ+1=cos2θ=1﹣sin2θ,
则5sin2θ﹣4sinθ=0,
∴sinθ=0,cosθ=﹣1或sin,cos,
当sinθ=0,cosθ=﹣1时,则0,
或sin,cos,则2.
故选:D.
5.已知:,则的值为 .
【解答】解:∵,
∴11,
故答案为 .
6.已知,其中α是第三象限角,且,则f(α)= .
【解答】解:∵tanα,
又∵,
∴sinα,
∵α是第三象限角,
∴cosα,
∴f(α)=﹣tanα.
故答案为:.
相关教案
这是一份高端精品高中数学二轮专题-数列求和(带答案)教案,共17页。
这是一份高端精品高中数学二轮专题-椭圆(带答案)教案,共20页。
这是一份高端精品高中数学二轮专题-函数图像(带答案)教案,共12页。












