初中数学华师大版八年级上册第14章 勾股定理14.2 勾股定理的应用教案

这是一份初中数学华师大版八年级上册第14章 勾股定理14.2 勾股定理的应用教案，共4页。
  14.2 勾股定理的应用执笔人：  审核：八年级数学组 课型：新授 时间：   1、知识与方法目标：通过对一些典型题目的思考、练习，能正确、熟练的进行勾股定理有关计算，深入对勾股定理的理解。2、过程与方法目标：通过对一些题目的探讨，以达到掌握知识的目的。　　3、情感与态度目标：感受数学在生活中的应用，感受数学定理的美。             
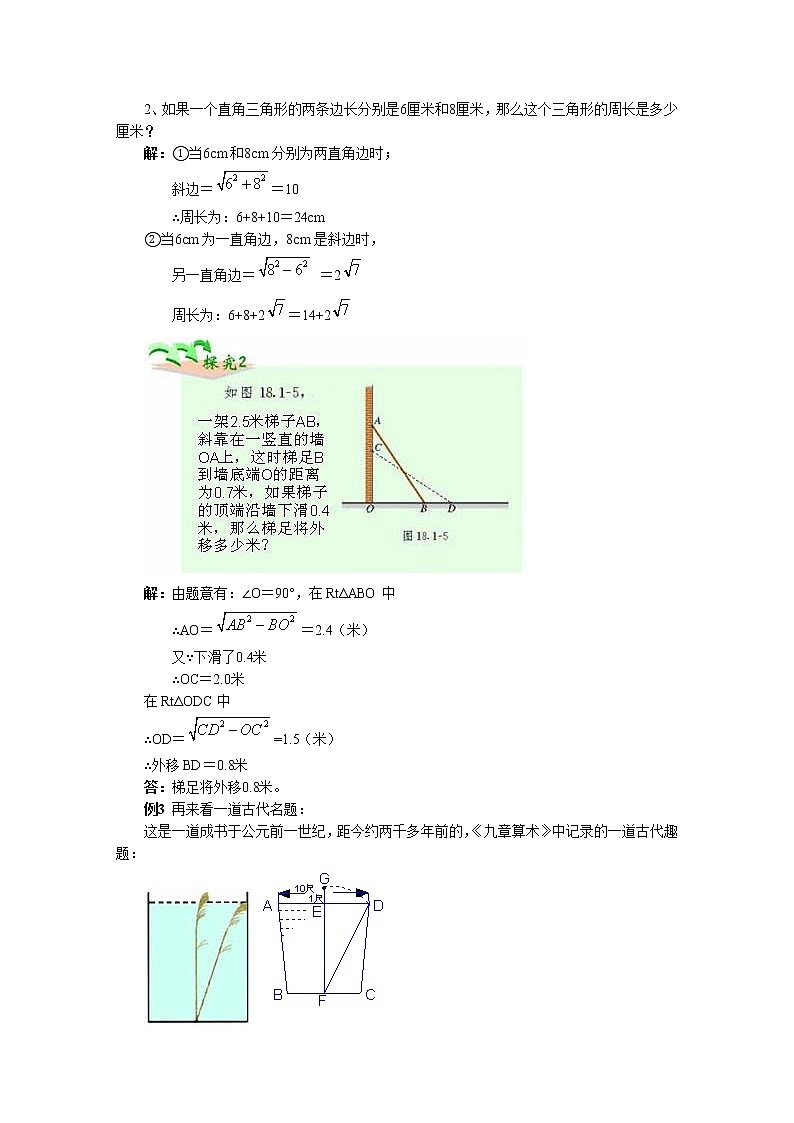
课前复习1、勾股定理的内容是什么？问：是这样的。在RtΔABC中，∠C＝90°，有：AC2+BC2＝AB2，勾股定理揭示了直角三角形三边之间的关系。今天我们来看看这个定理的应用。新课过程分析：大家分组合作探究：解：在RtΔABC中，由题意有：　　AC＝＝≈2.236　　∵AC大于木板的宽　　∴薄木板能从门框通过。学生进行练习：1、在Rt△ABC中，AB＝c，BC＝a，AC＝b， ∠B=90゜.①已知a=5，b=12，求c；②已知a=20，c=29，求b（请大家画出图来，注意不要简单机械的套a2+b2＝c2，要根据本质来看问题）2、如果一个直角三角形的两条边长分别是6厘米和8厘米，那么这个三角形的周长是多少厘米？解：①当6cm和8cm分别为两直角边时；　　斜边＝＝10　　∴周长为：6+8+10＝24cm②当6cm为一直角边，8cm是斜边时，　　另一直角边＝ ＝2　　周长为：6+8+2＝14+2解：由题意有：∠O＝90°，在RtΔABO中　　∴AO＝＝2.4（米）　　又∵下滑了0.4米　　∴OC＝2.0米在RtΔODC中∴OD＝=1.5（米）∴外移BD＝0.8米答：梯足将外移0.8米。例3 再来看一道古代名题：这是一道成书于公元前一世纪，距今约两千多年前的，《九章算术》中记录的一道古代趣题： “现在有一个贮满水的正方形池子，池子的中央长着一株芦苇，水池的边长为10尺，芦苇露出水面1尺。若将芦苇拉到岸边，刚好能达到水池岸与水面的交接线的中点上。请求出水深与芦苇的长各有多少尺？解：由题意有：DE＝5尺，DF＝FE+1。设EF＝x尺，则DF＝（x+1）尺由勾股定理有：x2+52＝（x+1）2解之得：x＝12答：水深12尺，芦苇长13尺。例4　如图，校园内有两棵树，相距12米，一棵树高16米，另一棵树高11米，一只小鸟从一棵树的顶端飞到另一棵树的顶端，小鸟至少要飞多少米？解：由题意有：BC＝12米，AC＝16－11＝5米。在RtΔABC中AB＝＝13答：小鸟至少要飞13米。三、作业：完成书P77页1，P78页2、3四、教学反思：