高中数学人教版新课标A必修4第二章 平面向量2.4 平面向量的数量积多媒体教学课件ppt

这是一份高中数学人教版新课标A必修4第二章 平面向量2.4 平面向量的数量积多媒体教学课件ppt，共20页。PPT课件主要包含了探求新知，巩固定义，总结性质，再探定义，实数乘法，交换律，结合律，分配律，向量的数量积，运算律等内容，欢迎下载使用。

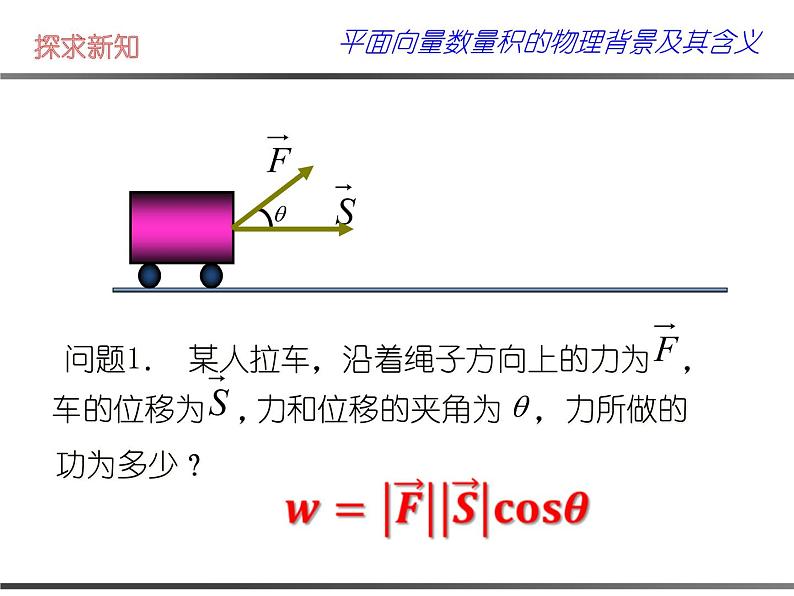
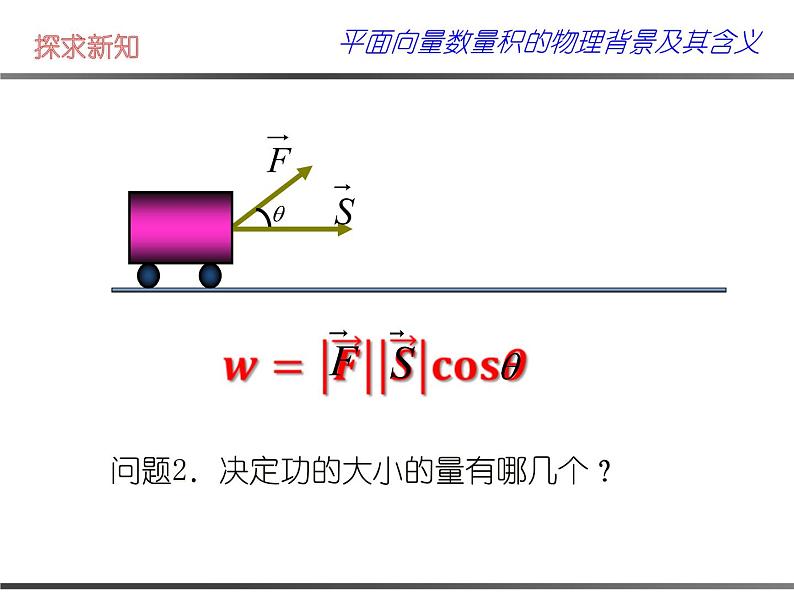
问题2．决定功的大小的量有哪几个？
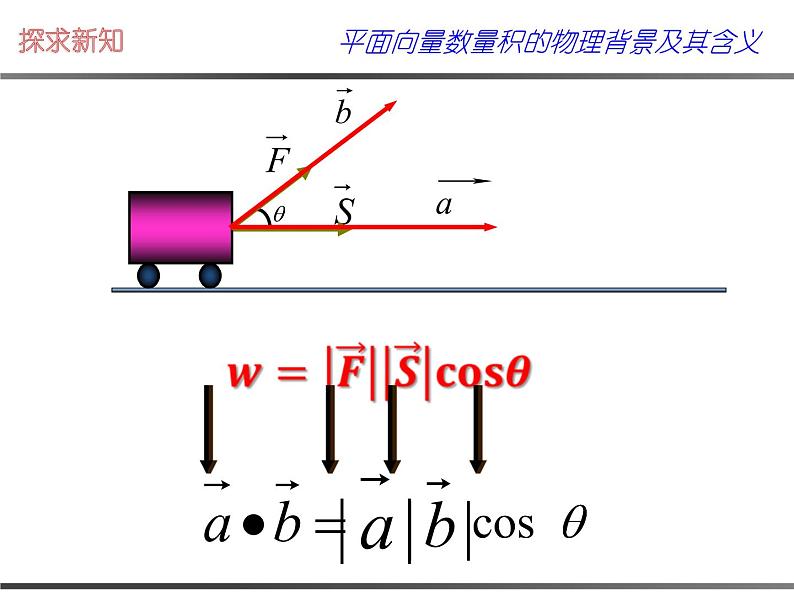
定义 已知两个非零向量 与 ，我们把数量 叫做向量 与 的数量积(或内积)，记作 ，即 ，其中 是 与 的夹角．
规定：零向量与任一向量的数量积为0．
问题3．决定向量数量积的大小的量有哪几个？
数量积的正、负、零由谁决定？
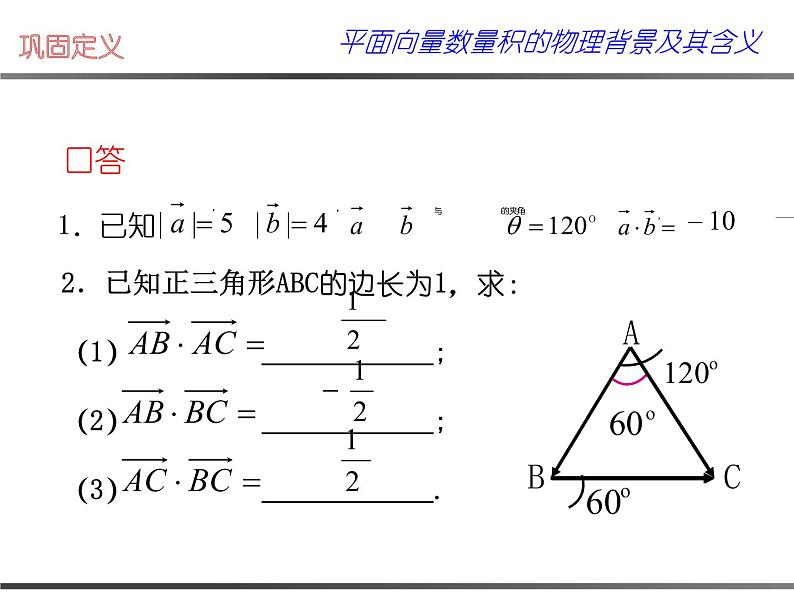
2．已知正三角形ABC的边长为1，求： （1） ; （2） ; （3） .
(2)若 与 同向，则 ； 若 与 反向，则 ； 特别地， ，
(4) .
(3)　　　　　　　　　；
平面向量数量积的几何意义
探究：数量积作为一种运算，有怎样的运算律呢？
平面向量数量积的运算律
向量a、b、a + b在c上的射影的数量分别是OM、MN、 ON, 则
1．若a=0，则对任一向量b ，有a · b=02．若a≠0，则对任一非零向量b,有a · b≠03.若a≠0，a · b=0,则b=04.若a · b=0,则a · b中至少有一个为05.若b≠0，a · b= b · c,则a=c6.若a · b= a · c ,则b≠c,当且仅当a=0时成立7对任一向量a,有a2=|a|2
( √ ）
( × ）
例3 已知︱ ︱＝3，︱ ︱＝4，且 与 不共线.求 当k为何值时，向量 ＋k 与 －k 互相垂直？