2021年中考数学二轮复习：勾股定理考点专题训练2（Word版 无答案）

这是一份2021年中考数学二轮复习：勾股定理考点专题训练2（Word版 无答案），共10页。试卷主要包含了选择题等内容，欢迎下载使用。
1.如果梯子的底端离建筑物5米,13米长的梯子可以到达建筑物的高度是( )
A.12米 B.13米 C.14米 D.15米
2.若△A B C的三边长 a ，b ，c满足(a－b )2＋|a 2＋b2－c2|＝0，则△ABC是( )
A．等腰三角形 B．直角三角形
C．等腰直角三角形 D．等腰三角形或直角三角形
3. 下列说法正确的是（ ）
A. 若是的三边，则
B. 若是的三边，则
C. 若 是的三边，，则
D. 若 是的三边，，则
4.下列各组数为勾股数的是
A. 7，12，13B. 3，4，7C. 8，15，17D. ，2，
5．在△ABC中，∠A，∠B，∠C的对边分别为a，b，c，下列条件中，能判断△ABC是直角三角形的是（ ）
A．∠A：∠B：∠C＝3：4：5B．a＝32，b＝42，c＝52
C．b＝c，∠A＝45°D．a2＝b2﹣c2
6.以下定理，其中有逆定理的是
A. 对顶角相等
B. 互为邻补角的角的平分线互相垂直
C. 如果一个角的两边与另一个角的两边分别平行，那么这两个角相等或互补
D. 直角三角形的两条直角边长的平方和等于斜边长的平方
7.将一根 24cm 的筷子，置于底面直径为 15cm ， 高 8cm 的装满水的无盖圆柱形水杯中，设筷子浸没在杯子里面的长度为 hcm ， 则 h 的取值范围是（ ）
A. h≤15cm B. h≥8cm C. 8cm≤h≤17cm D. 7cm≤h≤16cm
8. 如果下列各组数是三角形的三边，那么不能组成直角三角形的一组数是( )
A. 7,24,25 B. 3,4,5 C. 3,4,5 D. 4,7,8
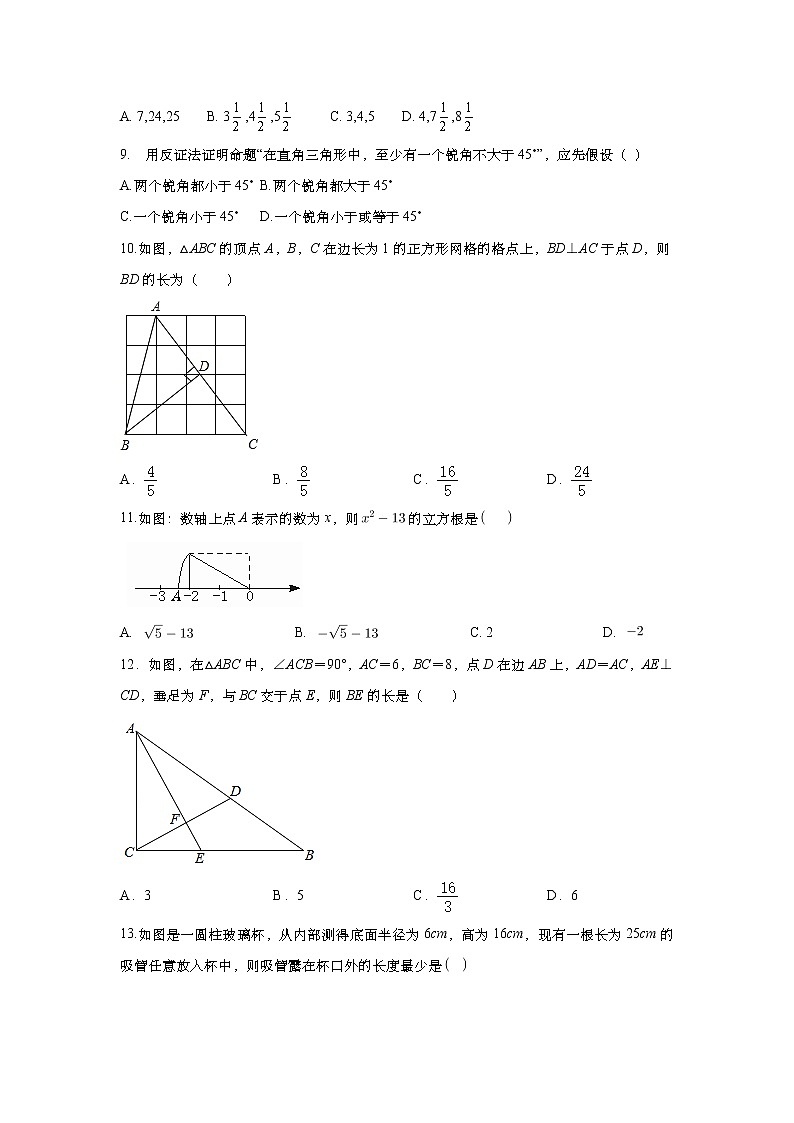
9. 用反证法证明命题“在直角三角形中，至少有一个锐角不大于45˚”，应先假设（ ）
A.两个锐角都小于45˚B.两个锐角都大于45˚
C.一个锐角小于45˚D.一个锐角小于或等于45˚
10.如图，△ABC的顶点A，B，C在边长为1的正方形网格的格点上，BD⊥AC于点D，则BD的长为（ ）
A．B．C．D．
11.如图：数轴上点A表示的数为x，则的立方根是

A. B. C. 2 D.
12．如图，在△ABC中，∠ACB＝90°，AC＝6，BC＝8，点D在边AB上，AD＝AC，AE⊥CD，垂足为F，与BC交于点E，则BE的长是（ ）
A．3B．5C．D．6
13.如图是一圆柱玻璃杯，从内部测得底面半径为6cm，高为16cm，现有一根长为25cm的吸管任意放入杯中，则吸管露在杯口外的长度最少是
A. 6cm B. 5cm C. 9cm D.
14．如图所示的是由两个直角三角形和三个正方形组成的图形，其中阴影部分的面积是（ ）
A．50B．16C．25D．41
15.如图，从笔直的公路旁一点P出发，向西走6km到达；从P出发向北走6km也到达．下列说法错误的是 （ ）
A．从点P向北偏西45°走3km到达
B．公路的走向是南偏西45°
C．公路的走向是北偏东45°
D．从点P向北走3km后，再向西走3km到达
16.如图，将三角形纸片ABC沿AD折叠，使点C落在BD边上的点E处若，则的值为
A. 4 B. 6 C. 10 D. 16
17．如图，四边形ABCD中，∠A＝90°，AD＝2，连接BD，BD⊥CD，垂足是D且∠ADB＝∠C，点P是边BC上的一动点，则DP的值可能是（ ）
A．B．1C．D．2
18. 如图，梯子斜靠在墙面上，，当梯子的顶端沿方向下滑米时，梯足沿方向滑动米，则与的大小关系是（ ）
A． B． C． D．不确定
19. 如图，小方格都是边长为1的正方形,则四边形ABCD 的面积是 ( )
A. 25 B. 12.5 C. 9 D. 8.5
20．如图，一架长2.5m的梯子AB靠在一竖直的墙上，这时梯子的底端A到墙根O的距离为0.7m，如果梯子的顶端B下滑0.4m至B'，那么梯子底端将滑动（ ）
A．0.6mB．0.7mC．0.8mD．0.9m
二．填空题
1．一个三角形三边满足（a+b）2﹣c2＝2ab，则这个三角形是 三角形．
2.已知三角形三边长为a，b，c，如果，则是____三角形．
3. 某直角三角形三条边的平方和为800，则这个直角三角形的斜边长为________．
4.在中，，，AD为BC边上的高，且，则的周长等于__________．
5.如图是一株美丽的勾股树，其作法为：从正方形①开始，以它的一边为斜边，向外作等腰直角三角形，然后再以其直角边为边，分别向外作两个正方形，计为②．依此类推…若正方形①的面积为16，则正方形③的面积是________．
6．如图，在等腰三角形ABC中，AB＝AC，AD是底边上的高，若AB＝5 cm，BC＝6 cm，则AD＝__________．

7. 如图，以一个直角三角形的三边为边长分别向外作三个正方形，如果两个较大正方形的面积分别是和，那么最小的正方形的面积为
8. 如图，有一圆柱体，它的高为8cm，底面周长为12cm．在圆柱的下底面A点处有一个蜘蛛，它想吃到上底面上与A点相对的B点处的苍蝇，需要爬行的最短路径是________cm．

9.我国古代数学著作《九章算术》中有这样一个问题：”今有池方一丈，葭（jiā）生其中央，出水一尺．引葭赴岸，适与岸齐．问水深几何？”（注：丈，尺是长度单位，1丈＝10尺）这段话翻译成现代汉语，即为：如图11，有一个水池，水面是一个边长为1丈的正方形，在水池正中央有一根芦苇，它高出水面1尺．如果把这根芦苇拉向水池一边的中点，它的顶端恰好到达池边的水面，则水池里水的深度是 尺．
10.如图，在四边形ABCD中，，，，则BD的长为 .
11．如图，在四边形ABCD中，AB＝BC＝2，AD＝2，∠B＝∠D＝90°，则CD＝ ．
12. 如图，是等边中的一个点，，则的边长是 .
三．解答题
1.如图，已知直角△ABC的两直角边分别为6，8，分别以其三边为直径作半圆，求图中阴影部分的面积．
2. 已知，如图，四边形ABCD中，AB=3cm，AD=4cm，BC=13cm，CD=12cm，且∠A=90°，求四边形ABCD的面积.
3. 如图，一只蚂蚁沿边长是3的正方体表面从顶点A爬到顶点B，求它走过的最短路程，并画出示意图．

4.如图，每个小正方形的边长都为1．
求四边形ABCD的周长；求的度数．

5. 如图，某斜拉桥的主梁垂直桥面于点，主梁上两根拉索，的长分别为米，米．

若拉索，求固定点，之间的距离；
若固定点，之间的距离为米，求主梁的高度．

6．如图，在Rt△ABC，∠ABC＝90°，AB＝16cm，BC＝12cm，BD⊥AC．
（1）求出AC的长和BD的长．
（2）点P从点C出发，以每秒1cm的速度沿C→A→B运动，运动到点B时停止，设运动时间为t秒，当t为何值时，△PBC的面积为36cm2？
7. 中，，，．若，如图1，根据勾股定理，则
．若不是直角三角形，如图2和图3，请你类比勾股定理，试猜想与的关系，并证明你的结论．
8. 如图，在中，，，是内的一点，且，求的度数．